步履式顶推钢箱梁垫块性能对比分析

2021-04-09朱利明黄国红

现代交通技术 2021年1期

陈君，吴波，朱利明，黄国红，徐松

(1. 江苏省南京市公共工程建设中心，南京 210009；2. 南京工业大学交通运输工程学院，南京 210009)

步履式顶推施工法具有安全程度高、顶推平稳、主梁轴线调整便利等优势，因而广泛运用于跨越深谷、河流、公路以及铁路等桥梁施工中[1-2]。在钢箱梁顶推施工过程中，主梁受自重效应或设置的预拱度等因素影响，主梁在垫块长度区域内的前后端会产生一定的竖向位移差值，这个高差定义为转角位移。转角位移反映出垫块和主梁底板的不均匀接触，这种不均匀接触会导致主梁支承区域出现屈服，对顶推施工过程的结构安全产生很大影响[3-4]。在桥梁顶推施工中，垫块的选择通常根据工程经验，这样不仅无法保证顶推过程中结构的安全，还会延长施工工期并增加施工成本，进而添加很多不必要的麻烦[5]。步履式顶推施工过程中因垫块参数选择不当，造成主梁支承区域局部应力超限，钢箱梁底板被顶凹的情况也很多，因此分析垫块参数对钢箱梁局部受力的影响就显得尤为重要。

谢祺[5]认为选择弹性模量较小的垫块，可有效改善支承处接触不均匀的现象，垫块的长度越长对支承处的局部受力就越有利；李传习等[6]认为垫块在设计面积条件下，其弹性模量减小至钢材的60%时，支承位置处钢梁局部受力改善显著，垫块宽度的大小对支承处的局部受力无显著影响；李兴全等[7]分别分析4种垫块对钢箱梁局部受力的影响，建议采用Ⅱ类橡胶垫块或聚四氟乙烯板作为弹性垫层；蒋雄[8]在对比设置橡胶垫块和不设橡胶垫块两种情况后认为设置橡胶垫块可有效改善钢箱梁局部受力问题。目前，步履式顶推施工垫块的选择主要根据工程经验，针对垫块参数对钢箱梁局部受力的影响研究较少，本研究以南京龙翔西立交建设工程为背景，基于通用有限元软件ABAQUS建立典型不利工况下“壳-实体-接触”混合有限元模型，分析步履式顶推施工中垫块参数对钢箱梁局部应力的影响，提出垫块参数的合理取值，其结果可为相关工程设计及步履式顶推施工提供参考。

1 工程背景

南京龙翔西立交建设工程，其上部结构采用简支钢箱梁，跨径为60 m，在两端过渡墩处均与现浇预应力混凝土箱梁连接。钢箱梁采用步履式顶推施工，顶推距离为(6.7+39+60)m，顶推立面布置如图1所示。桥面总宽为38.5 m，左右对称，桥面设双向2%横坡，采用双箱断面，每个箱体3个箱室，主梁高度为2.6 m，单个箱体底板宽度为 12.625 m，两个箱体间隔为5.5 m。根据钢箱梁分体宽幅的结构特点，在主梁梁底设置横向4支点步履式顶推设备，每套顶推设备采用单个竖向千斤顶和水平千斤顶，竖向千斤顶直径为320 mm，水平千斤顶直径为140 mm，步履式顶推设备上未布设分配梁或垫梁，其上直接布置钢垫块和其他垫块，钢垫块和其他垫块接触面积相同。顶推过程中，步履式顶推设备中轴线与中腹板对齐，纵向顶推步距为0.6 m，滑道处钢箱梁横截面如图2所示。

图1 顶推立面布置(单位：mm)

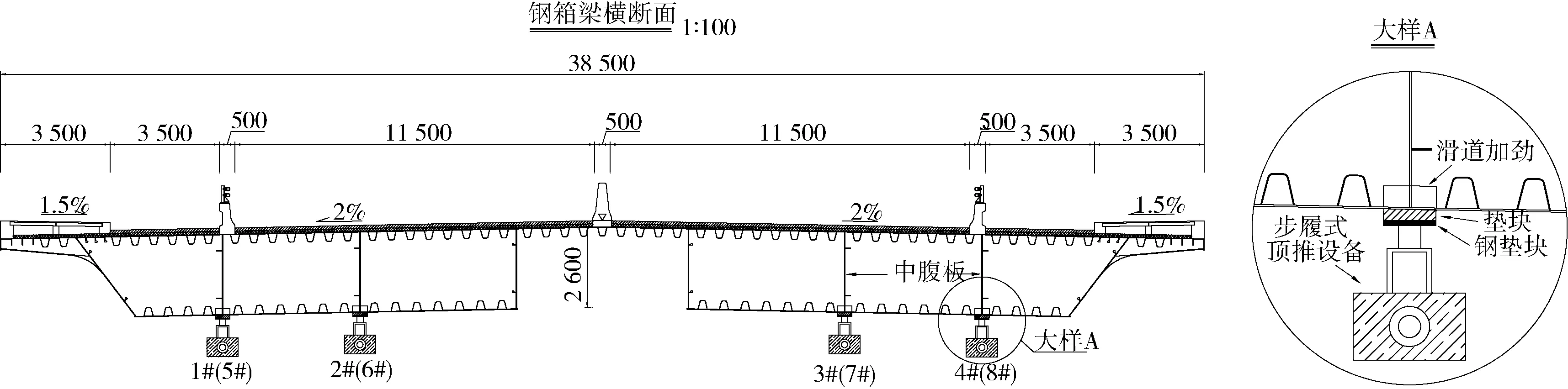
图2 滑道处钢箱梁横截面(单位：mm)

2 结构有限元分析

2.1 顶推施工全过程仿真分析

2.1.1 建立有限元整体模型

采用midas Civil有限元软件建立空间计算分析模型，杆系有限元模型如图3所示，主梁、导梁采用空间梁单元模拟，对桥梁整个顶推过程进行施工模拟，采用“墩动梁不动”方式模拟桥梁顶推过程，以每顶推1 m作为1个计算步长，施工计算模拟共划分108个施工阶段。该模型采用直角坐标系，X轴为纵桥向，Y轴为横桥向，Z轴为竖桥向。顶推过程中支承位置对钢箱梁的约束，采用“弹性约束”中的“仅受压”，前导梁前端约束Y的平动和X、Z的转动、后导梁后端约束X、Y的平动和X、Z的转动。

图3 杆系有限元模型

2.1.2 典型不利工况的确定

通过全过程仿真分析，以主梁“悬臂端挠度+支反力”综合确定典型不利工况，典型不利工况发生在顶推64.5 m工况下(即前导梁即将抵达M08墩时)，此时主梁前端挠度为-52.8 mm(挠度以向上为正，向下为负)，反力最大值发生在M09墩，数值达到10 725.5 kN。

2.2 “壳-实体-接触”混合有限元模型

2.2.1 建立有限元局部模型

顶推过程中，钢箱梁与导梁连接为一个整体，本文选取60 m钢箱梁，采用大型通用软件ABAQUS建立“壳-实体-接触”混合有限元模型，如图4所示，分析顶推过程中垫块参数对钢箱梁局部应力的影响。钢箱梁段采用壳单元S4R、S3R，垫块采用实体单元C3D8R。主梁模型网格尺寸为0.2 m，垫块模型网格尺寸细化为0.1 m。钢箱梁、钢垫块的密度均为7 850 kg/m3，弹性模量E取206 GPa，泊松比μ取0.3, 垫块布置如图5所示。

图4 “壳-实体-接触”混合有限元模型

图5 垫块布置

2.2.2 边界条件的模拟

在ABAQUS“壳-实体-接触”混合有限元模型中，主梁两端各建立1个参考点，参考点与主梁两端节点采用耦合约束的方式连接在一起[9]，耦合约束放大图如图6所示。钢箱梁与垫块的相互作用，接触类型采用面-面离散方式约束，法向硬接触，切向无摩擦，以刚度较大的钢箱梁底板接触面作为主面，垫块顶面作为从面，面-面接触局部放大图如图7所示；垫块底面固结，未考虑步履式顶推装置具体细节及钢垫块。该模型采用直角坐标系，X轴为横桥向，Y轴为竖桥向，Z轴为纵桥向。主梁前端参考点约束X方向的平动和Y、Z方向的转动；主梁后端参考点约束X、Z方向的平动和Y、Z方向的转动[10-11]。

图6 耦合约束放大图

图7 面-面接触局部放大图

2.2.3 计算荷载

提取midas Civil整体模型顶推64.5 m工况下，主梁两端截面的剪力和弯矩，将其加载至ABAQUS模型对应的主梁两端截面参考约束点上；重力加速度取9.8 m/s2。

3 垫块参数对比分析

3.1 垫块面积对钢箱梁局部受力的影响

3.1.1 计算模型的建立

本节基于ABAQUS“壳-实体-接触”混合有限元模型分析5种垫块接触面积对钢箱梁局部受力的影响，垫块面积分别为：200 mm×200 mm；400 mm×400 mm；600 mm×600 mm；800 mm×800 mm；1 000 mm×1 000 mm。根据工程经验，垫块厚度暂取为100 mm，垫块弹性模量暂取为钢垫块的弹性模量(E=206 000 MPa)。

3.1.2 计算结果分析

顶推施工中，钢垫块通常用于调整主梁支点标高，其他垫块布置于钢垫块之上，直接与主梁梁底接触，垫块的面积直接影响着主梁支承区域局部效应，因此本节针对垫块面积对钢箱梁局部受力进行初步分析。主梁主要构件在不同垫块边长下最大等效应力趋势如图8所示。

图8 主梁主要构件在不同垫块边长下最大等效应力趋势

由图8可知：

(1) 各主要构件在垫块边长为600 mm工况下，最大等效应力由大到小依次排序为腹板、底板U肋、滑道加劲、底板、横隔板、顶板、顶板U肋。腹板的等效应力最大，这是因为垫块和主梁底板的接触区域内，由于支反力的作用使底板产生凸起，而在底板上恰好有一块腹板，底板的凸起被腹板限制，从而使底板和腹板连接处产生应力集中。

(2) 随着垫块边长的增加，腹板等效应力有明显降低趋势，垫块边长增加至400 mm以后腹板等效应力稳定于290 MPa左右，垫块长度增加至1 000 mm 后，腹板等效应力达到最小值270 MPa，这是因为垫块边长的增加，使垫块和底板的支承接触区域达到底板U肋处，底板U肋相应承担一部分作用力；底板U肋等效应力有增长趋势，这是因支承接触区域离底板U肋越来越近导致；底板和滑道加劲始终在125 MPa附近波动，无明显趋势；远离支承区域的横隔板、顶板、顶板U肋无明显等效应力变化。

(3) 垫块面积的选择不但要满足钢箱梁应力限值的要求，还要从经济性和适用性去考虑，当垫块边长达到400 mm时性价比最高，但考虑到垫块面积应留有一定的安全储备面积，综合确定垫块边长为600 mm时较为合适。

3.2 垫块厚度对钢箱梁局部受力的影响

3.2.1 计算模型的建立

在3.1节分析中，综合确定垫块边长为600 mm时为较合适的垫块面积，本节基于上述研究，分析5种垫块厚度对钢箱梁局部受力的影响，垫块厚度分别为20 mm、40 mm、60 mm、80 mm和100 mm。根据工程经验，垫块弹性模量暂取为钢垫块的弹性模量(E=206 000 MPa)。主梁主要构析在不同垫块厚度下最大等效应力趋势如图9所示；垫块在不同厚度下最大等效应力趋势如图10所示。

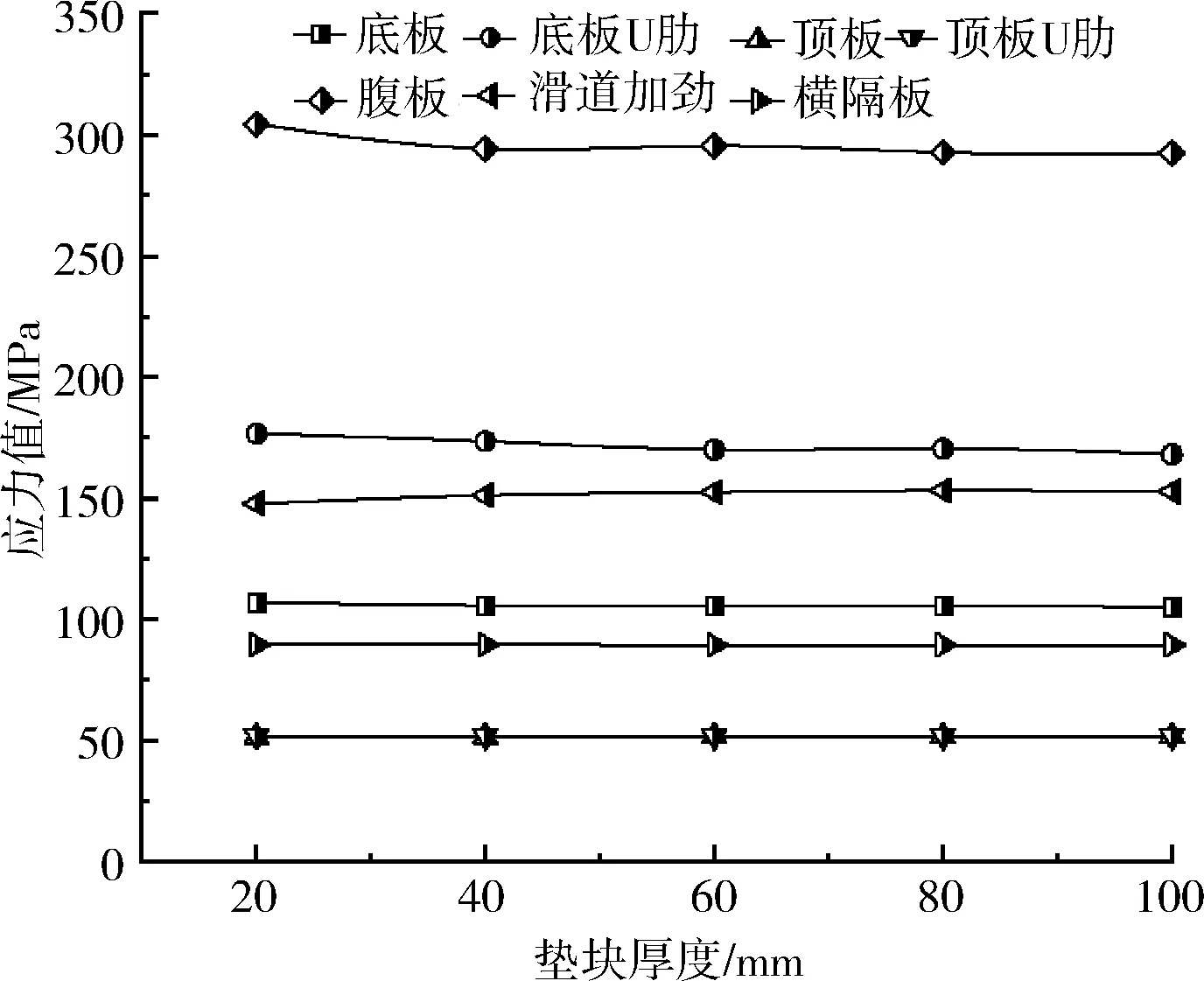
图9 主梁主要构件在不同垫块厚度下最大等效应力趋势

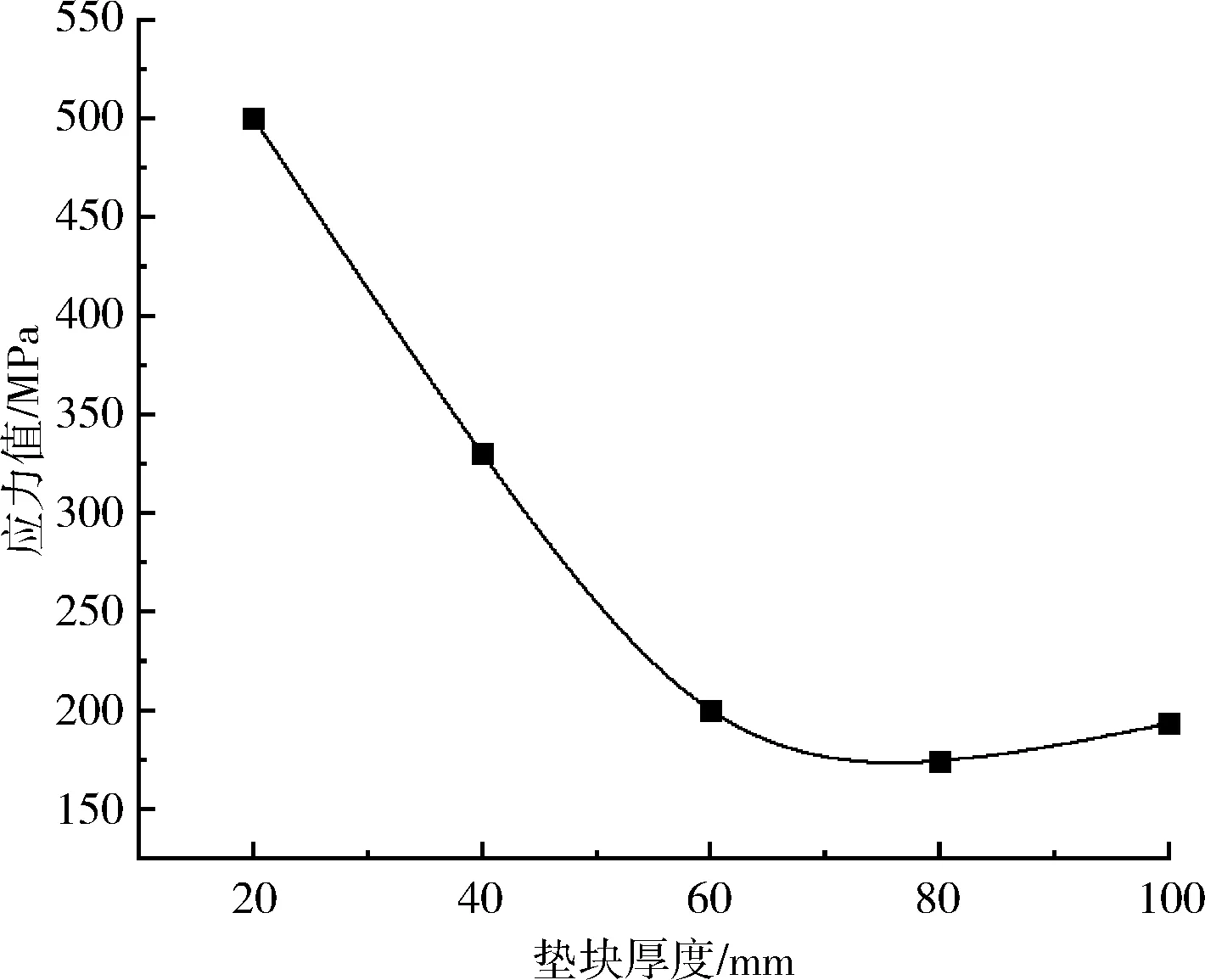
图10 垫块在不同厚度下最大等效应力趋势

3.2.2 计算结果分析

由图9和图10可知：

(1) 垫块厚度的增长对主梁各主要构件最大等效应力无显著影响。

(2) 垫块厚度的增长对垫块本身等效应力影响较大，并且总体呈递减趋势。当垫块厚度达到80 mm 时，垫块等效应力达到最小值174.7 MPa，因此选取垫块厚度为80 mm为合适的垫块厚度。

3.3 垫块刚度对钢箱梁局部受力的影响

3.3.1 计算模型的建立

在3.1节和3.2节分析中，综合确定垫块边长为600 mm、垫块厚度为80 mm为合理的垫块尺寸，本节基于上述研究分别选取4种垫块刚度，研究对钢箱梁局部受力的影响。在垫块尺寸相同的情况下，其刚度的大小主要取决于弹性模量，因此选取垫块分别为Ⅰ类橡胶垫(E=30 MPa)、Ⅱ类橡胶垫(E=500 MPa)、聚四氟乙烯板(E=1 420 MPa)和钢板(E=206 GPa)。

3.3.2 计算结果分析

垫块在主梁自重荷载作用下产生压缩变形，以此来自适应主梁梁体线形的变化，从而保证主梁底板和垫块顶面产生较好的贴合，通过改变垫块的弹性模量，从而避免主梁局部应力集中现象。不同垫块应力如图11所示。

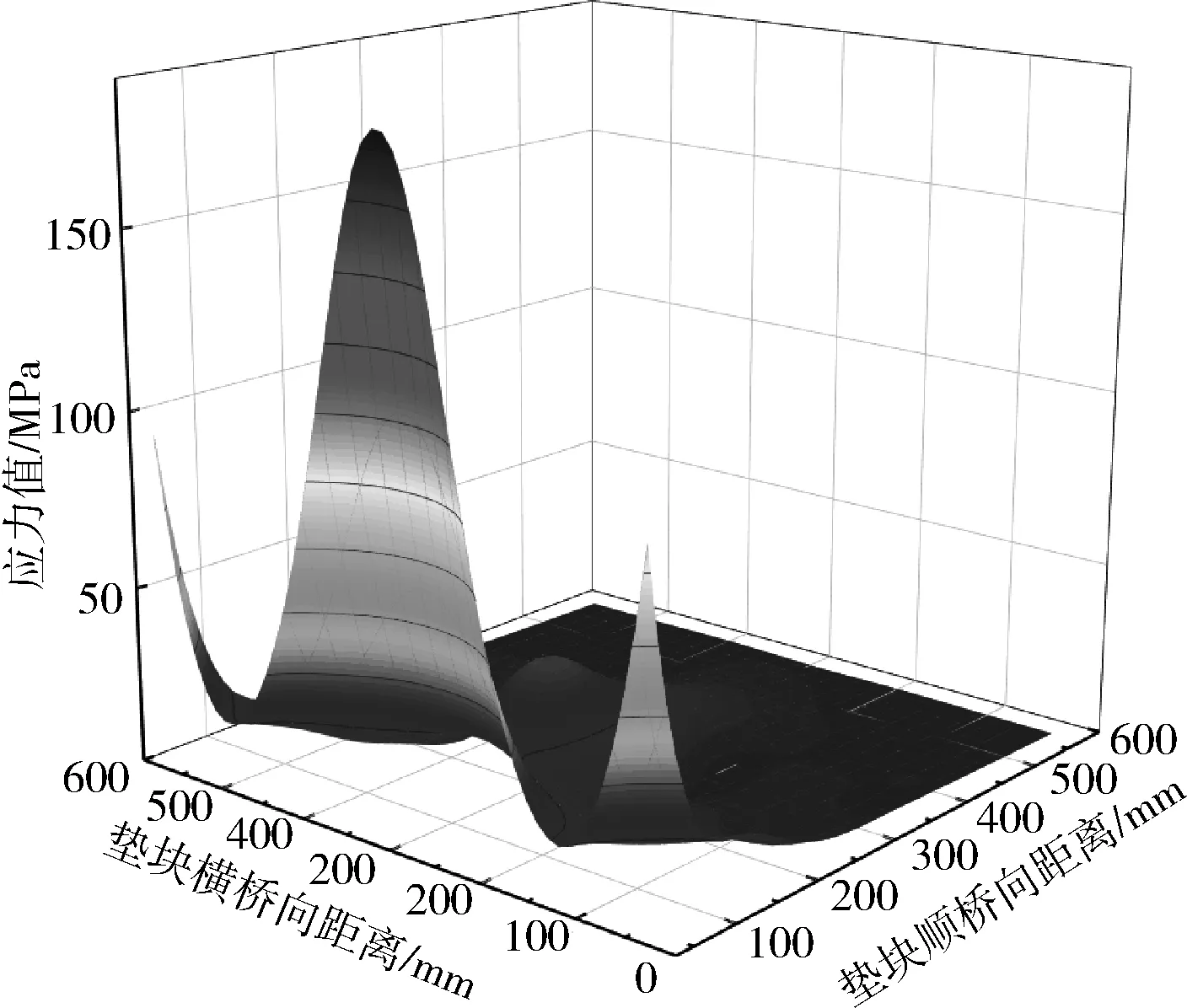
(a) 钢板垫块(E=206 GPa)应力

由图11可知：

(1) 垫块采用钢板垫块(E=206 GPa)时，垫块等效应力在垫块横、顺桥向上受力分布极不均匀；当垫块在顺桥向距离为0 mm、横桥向距离为300 mm 时，垫块等效应力出现最大值，这是因为在垫块和主梁底板接触时，底板的变形受到中腹板的限制，使垫块受力不均匀，从而造成垫块的应力集中。

(2) 当垫块弹性模量减小时，垫块和主梁底板的接触受力变得越来越均匀，主梁的接触受力区域变大，使垫块的应力水平变得更加均匀。

主梁主要构件在不同垫块弹性模量下最大等效应力趋势如图12所示。

图12 主梁主要构件在不同垫块弹性模量下最大等效应力趋势

由图12可知：

(1) 当垫块弹性模量为206 GPa时，腹板最大等效应力达到292.7 MPa，超过Q345钢材基本允许应力210 MPa[6]；随着垫块弹性模量的降低，当垫块弹性模量为1 420 MPa、500 MPa和30 MPa时，腹板最大等效应力分别对应为197.2 MPa、175.2 MPa和170.0 MPa，应力计算结果满足要求。

(2) 垫块弹性模量的减小，使腹板最大等效应力显著降低，这是因为垫块通过自身的压缩变形来适应梁体和垫块的相对变形，使钢箱梁接触区域内受力变得更加均匀；底板等效应力增加，这是因为腹板和底板共同受力，腹板竖向荷载的减小使得垫块范围内，腹板外其他部位底板竖向荷载比例增加；垫块弹性模量对主梁其他主要构件无明显等效应力变化影响。

(3) 垫块弹性模量不可过小，当弹性模量较小时，主梁会将垫块“压扁”，从而使钢垫块直接受力，反而起不到改善主梁局部应力的效果，因此，钢垫块和其他垫块宜采用相同的面积尺寸。

(4) 垫块的弹性模量为500 MPa或1 420 MPa时，可以很好地改善因转角位移所导致的主梁局部应力集中现象。