一种PolSAR图像G0分布参数估计新方法

崔浩贵，晏 庆，张 晓，杨 飞，范路芳

(中国人民解放军91001部队，北京 100841)

0 引言

极化合成孔径雷达(Polarimetric Synthetic Aperture Radar，PolSAR)杂波统计建模及其参数估计方法是PolSAR图像相干斑抑制[1]、分类识别[2-3]和目标检测[4]等图像解译手段的重要课题。在PolSAR图像中，均匀区域一般用高斯模型进行建模，而非均匀区域常用多变量乘积模型来进行非高斯建模。多变量乘积模型将PolSAR复散射向量表示为一个纹理分量和一个服从复高斯分布的相干斑分量的乘积，并且二者之间相互统计独立。G0分布模型[5-6]是应用非常广泛的PolSAR图像非高斯统计模型，它是在假设纹理分量服从逆Gamma分布时根据多变量乘积模型得到的。G0分布模型特别适用于城区等极不均匀区域的统计建模。

寻找快速、准确的参数估计是G0分布模型研究的核心问题。根据采用的数据源，可将G0分布参数估计方法分为单极化估计方法和全极化估计方法。其中传统的单极化估计方法分别估计出每个极化通道的参数，然后将各通道的参数求平均。而全极化估计方法利用了各通道之间的极化信息，其估计性能优于单极化的方法。目前最常用的全极化估计方法是Anfinsen等提出的基于协方差矩阵的对数累积量(Matrix Log Cumulants，MLC)的参数估计方法，该方法本质上是协方差矩阵行列式值的Mellin变换[7-11]。最近，Khan等人[12]将基于多视极化白化滤波器(Multilook Polarimetric Whitening Filter，MPWF)的参数估计方法扩展到分数阶矩(Fractional Moments，FM)的情形，提出了基于多视极化白化滤波器分数阶矩(MPWF-FM)的参数估计方法。实验结果表明，该方法比MLC方法具有更小估计方差和均方误差(Mean Square Error，MSE),但是该方法存在计算复杂、最优的分数阶矩无法理论推导得到和当纹理参数较小时失效等问题。

本文提出了一种基于多视极化白化滤波器对数累积量(Log Cumulants of MPWF，MPWF-LC)的参数估计新方法。新方法解决了MPWF-FM方法存在的估计失效等问题，并且具有更优的估计性能。通过G0分布数据和实测数据分别进行了仿真分析，结果有效验证了新方法的参数估计结果准确度高、计算速度快。

1 PolSAR图像乘积模型

PolSAR系统在测量中获取的信息可用复散射向量k表示：

k=[Shh,Shv,Svh,Svv]T，

(1)

式中，[·]T表示向量的转置；Sxy表示发射极化方式为x，接收极化方式为y的复散射系数；h表示水平极化；v表示垂直极化。

多变量乘积模型常用来对PolSAR图像进行非高斯建模，它将复散射向量表示为相互统计独立的纹理分量τ和相干斑分量y的乘积，即：

(2)

式中，y服从复高斯分布，其概率密度函数为：

(3)

式中，d是复高斯矢量的维数；Γ=E{yyH}，E{·}表示随机变量的数学期望。

实际中，为了抑制相干斑，常对图像进行多视处理，其过程可表示为：

(4)

式中，L为视图数，L≥d；上标“H”表示共轭转置；l代表第l个像素点。假设进行多视处理的像素点具有相同纹理分量，此时式(4)可简化为：

C=τY，

(5)

其中，

(6)

式中，Y服从Wishart分布，其概率密度函数为：

(7)

式中，d是Y的维数；Γ=E(Y)；Tr(·)表示矩阵的迹；函数Γd(L)为复数形式的多变量伽马函数：

(8)

式中，Γ(·)为标准Eular伽马函数。由于这里假设在多视窗口内纹理分量恒定，样本的协方差矩阵可表示为：

Σ=E{C}=E{τ}E{Y}=E{τ}Γ。

(9)

当式中纹理分量服τ为逆伽马分布，即τ～γ-1(u,α)时，其乘积模型服从G0分布。

2 基于MPWF对数累积量的参数估计方法

MPWF滤波器通过最优地组合极化协方差矩阵中的所有元素，得到一幅降斑的图像[13-14]。进行MPWF滤波后的数据可表示为：

(10)

将式(5)和式(9)代入式(10)，MPWF滤波后的数据可分解为：

(11)

x～γ(d,Ld)，

(12)

其中，伽马分布γ(u,d)的概率密度分布函数为：

(13)

基于Mellin变换的对数累积量定义为：

(14)

式中，kr{z}表示随机变量z的第r阶对数累积量；E{zs-1}为关于随机变量z的数学期望。当随机变量服从如式(11)所示的乘积模型时，其对应的对数累积量为加性模型[8]：

(15)

由于随机变量x服从如式(12)所示的伽马分布，可得其对数累积量为：

(16)

式中，ψ(x)=Γ′(x)/Γ(x)为digamma函数；Γ(x)为伽马函数。ψ(m,x)表示m阶Polygamma函数：

(17)

(18)

将式(16)、式(18)代入式(15)，可得基于MPWF对数累积量(MPWF-LC)的G0分布参数估计方法为：

(19)

(20)

3 仿真结果与分析

用G0分布仿真数据比较以下几种方法的相对估计偏差、相对估计方差、相对MSE和计算时间：

① MPWF-FM[12]；

② MLC方法，取二阶MLC进行参数估计[8]；

③ 本文提出的MPWF-LC参数估计方法，取二阶对数累积量的表达式，即在式中取r=2。

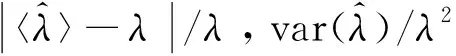
(a)相对估计偏差

图1 G0分布情形，不同参数λ下3种估计方法的相对估计偏差、相对估计方差与相对MSEFig.1 The relative estimation bias, relative estimation variance and relative MSE for three estimation methods with different parameters of λ in the case of G0 distribution

G0分布下各估计方法在不同样本数下的计算时间如图2所示。

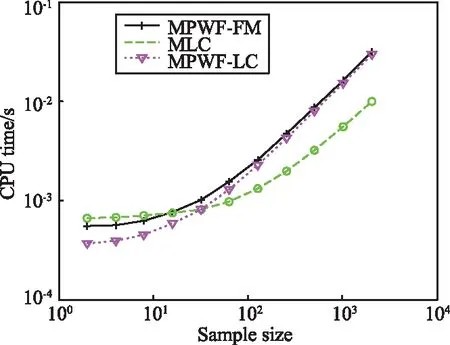
图2 各估计方法的计算时间比较Fig.2 Comparison of calculation time of different estimation methods

仿真数据参数L=10，λ=10。采用Matlab进行编程计算，计算机CPU为Intel E5700，双核3 GHz，内存大小2 GB。由图2可以看出，当样本数较小时，MPWF-LC计算所花的时间最短，计算复杂度最低；随着样本数的增加，当样本大于100后，MLC具有最短的计算时间；另外，在任意样本数下，MPWF-FM所需的计算时间最长。

4 实测数据分析

用实测数据对MPWF-LC，MPWF-FM和MLC三种方法进行分析。选取的实测数据为AIRSAR系统于1989年获得的Flevoland地区L波段PolSAR图像(12.1 m×6.7 m)，以及1988年获得的San Francisco地区的L波段PolSAR图像(10 m×10 m)。对原始数据进行了L=4(2×2)的多视处理，由于Flevoland地区的数据源为4视数据，因此其视图数变为L=16。

采用基于对数累积量的假设检验方法对实测数据进行拟合分析。简单假设检验情形下，统计量Qp可表示为：

Qp=n(〈k〉-k)TK-1(〈k〉-k)，

(21)

式中，〈k〉为样本的MLC，k为特定模型下MLC的理论值；n为样本数；下标p为〈k〉或k的维数，K=nE{(〈k〉-k)(〈k〉-k)T}。可知Qp服从自由度为p的χ2分布[15]：

Qp→χ2(p)。

(22)

假设检验中的概率值(Probability Value，p值)是指在由H0所规定的总体中随机抽样，获得等于及大于现有统计量的概率。由上述分析可知，p值可由统计量Qp根据χ2(p)分布计算得到。在参数估计中视图数L用名义视图数代替，向量〈k〉和k采用2阶和3阶MLC，即〈k〉=[〈k2〉,〈k3〉]T，k=[k2,k3]T。

在2幅图像中各选取了4个大小为20 pixel×20 pixel的区域进行参数估计与假设检验，比较各参数估计方法在G0分布假设下的p值。图3和图4分别给出了2幅图像中4个区域的选择以及各区域的样本对数累积量〈k〉。如图3(a)所示，Flevoland图像中选取的4个区域分别为河流、森林、小麦和油菜籽区域[16]。由图3(b)可知，河流的MLC靠近G0分布，森林的MLC靠近K分布，而小麦和油菜籽区域与Wishart、K和G0分布都非常接近。如图4(a)所示，San Francisco图像中选取的4个区域分别为海洋、城区、植被1和植被2。由图4(b)可知，海洋的MLC靠近Wishart分布，城区的MLC靠近G0分布，而植被1和植被2靠近K分布。

(a)4个区域的示意(Pauli RGB图像)

(a)4个区域的示意(Pauli RGB图像)

Flevoland四个区域在G0分布模型下的参数估计结果及假设检验p值如表1所示。由表1可以看出，对于河流区域，所有估计方法得到的p值都能通过显著性水平α=0.05的假设检验，但是MLC方法的p值最大。对于小麦和油菜籽区域，所有估计方法的p值都较大。森林区域同样地无法通过显著性水平α=0.05的假设检验。

表1 Flevoland四个区域在G0分布模型下的参数估计结果及p值

San Francisco四个区域在G0分布模型下的参数估计结果及假设检验p值如表2所示。由表2可以看出，对于城区，只有MLC方法的p值都能通过显著性水平α=0.05的假设检验，其他2种方法p值很小。对于海洋区域，3种方法的结果都能通过显著性水平α=0.05的假设检验，但是MLC方法的p值略小。植被1和植被2区域，所有估计方法的p值都无法通过显著性水平α=0.05的假设检验。

表2 San Francisco四个区域在G0分布模型下的参数估计结果及p值

从上述分析可以看出，MPWF-LC和MPWF-FM方法的参数估计结果和p值都非常接近。而MLC方法在某些区域表现较好，例如Flevoland图像中的河流和San Francisco图像中的植被2区域，这是因为该参数估计方法和假设检验都是基于MLC。在其他区域，MLC方法和另外2种方法的结果也基本上相差不大。从该结果可以看出，本文提出的MPWF-LC方法在实测数据参数估计中的有效性。

5 结束语

以多视极化白化滤波器和对数累积量为基础，提出了基于多视极化白化滤波器对数累积量的G0分布模型的参数估计方法。用仿真数据和实测数据对本文方法与MLC方法以及MPWF-FM方法进行了比较。实验结果表明，本文方法具有最小的估计方差和MSE，并且在样本数较少时，计算时间最短。另外，可以将本文方法应用于Fisher分布、U分布等PolSAR图像模型，其推导结果及估计效果值得研究。