一类含二阶导数的中值问题中辅助函数的构造

陈思源

(西安思源学院 基础部，陕西 西安 710038)

证明中值问题可以锻炼学生的逆向思维以及转化数学问题的能力，一般需要借助辅助函数来完成证明。辅助函数可以帮我们简化问题，挖掘题目中的隐藏条件，让我们站在“明处”观察、分析和解答所要求解的问题[1-2]。但是，辅助函数的构造却是难点，同学们普遍反映无从下手。那么如何根据题目留下的蛛丝马迹去寻找辅助函数呢？辅助函数的构造过程可以很好地锻炼学生的数学思维。优质的数学教学，就是让学生掌握数学的思维，即演绎思维。这种思维是在假设和结构之间找出一条推理的链，这种链常常是由多个推理所构成的逻辑链，只要其中一个链断裂，演绎就不成立。解决问题就是寻求这种推理的链，这是一种技巧、灵感和智慧，是一种深不见底的功夫，因此需要细讲精练[3]。下面主要通过相关试题讨论一类含二阶导数的中值问题中辅助函数的构造方法。

1 一类含二阶导数的中值问题中辅助函数的构造

证明含一个中值点的中值问题时，一般是通过构造辅助函数用罗尔定理解决。那么如果要证明含二阶导数的中值问题F(ξ,f(ξ),f′(ξ),f″(ξ))=0时，如何去寻找辅助函数呢？关于这类问题，我们常见的题型有以下两种。

1.1 第一种题型中辅助函数的构造

第一种是证明等式F(ξ,f′(ξ),f″(ξ))=0。

我们先分析微分方程F(x,f′(x),f″(x))=0，这是一个关于f′(x)的一阶方程，然后再求出通解G(x,f′(x))=C，最后辅助函数可构造为：

H(x)=G(x,f′(x))

例1 设函数f(x)在[0,1]上具有二阶导数，且f(0)=f(1)，那么至少存在一点ξ∈(0,1)，使得2f′(ξ)+(ξ-1)f″(ξ)=0成立。

按照上面所述的方法，我们先根据结论得到微分方程：

2f′(x)+(x-1)f″(x)=0

令y=f′(x)，则有：

求得通解为：

y(x-1)2=C

即(x-1)2f′(x)，从而辅助函数为：

F(x)=(x-1)2f′(x)

证明：令

F(x)=(x-1)2f′(x)

由于函数f(x)在区间[0,1]上具有二阶导数，因此f(x)在区间[0,1]上连续，在区间[0,1]内可导，又：

f(0)=f(1)

由罗尔定理，至少有一点x0∈(0,1)使得f′(x0)=0成立。

又已知，F(x)在区间[x0,1]上连续，在(x0,1)内可导，且

F(x0)=F(1)=0

再由罗尔定理，至少存在一点ξ∈(x0,1)⊂(0,1)使得：

f′(ξ)=0

从而可得：

2f′(ξ)+(ξ-1)f″(ξ)=0

1.2 第二种题型中辅助函数的构造

第二种是证明等式F(ξ,f(ξ),f′(ξ),f″(ξ))=0，其中F为线性函数。

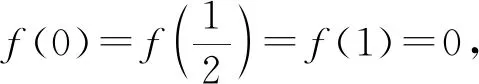
这类题型，我们可以采用组合降阶的方法去寻找辅助函数，具体的分析过程如下例所示。

先从结论中得到微分方程

f″(x)+3f′(x)+2f(x)=0

等号右边的项组合成下列形式：

[f′(x)+2f(x)]′+[f′(x)+2f(x)]=0

令y=f′(x)+2f(x)，则有：

y′+y=0

求得通解为：

y=Ce-x

即ex[f′(x)+2f(x)]=C，从而辅助函数为：

G(x)=ex[f′(x)+2f(x)]

将以上函数用罗尔定理处理就能得到要证明的结论，但是它满足罗尔定理的条件吗？若要满足

G(x1)=G(x2)

则需f′(x1)+2f(x1)=f′(x2)+2f(x2)。

通过对题目已知的分析，我们可以尝试证明

f′(x1)+2f(x1)=f′(x2)+2f(x2)=0

根据以上等式的形式，令f′(x)+2f(x)=0，得通解

f(x)=Ce-2x

从而

f(x)e2x=C

因此再做辅助函数

F(x)=f(x)e2x

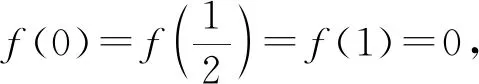
f′(ξ1)=0,f′(ξ2)=0

即有

f′(ξ1)+2f(ξ1)=f′(ξ2)+2f′(ξ2)=0

于是G(x)=ex[f′(x)+2f(x)]在区间[ξ1,ξ2]上满足罗尔定理，故存在

ξ∈(ξ1,ξ2)⊂(0,1)

使得G′(ξ)=0，即

f″(ξ)+3f′(ξ)+2f(ξ)=0

例3.(2013年全国研究生入学考试数学一试题)设奇函数f(x)在[-1,1]上具有二阶导数，且f(1)=1，证明：(1)存在一点ξ∈(0,1)，使得f′(ξ)=1；(2)存在一点η∈(-1,1)，使得f″(η)+f′(η)=1。

试题的第二问应该如何思考呢？下面分析其辅助函数的构造方法。根据要证明的结论，我们得到微分方程：

f″(x)+f′(x)=1

先用降阶法求解导函数满足的关系式。令f′(x)=y于是得到：

y′+y=1

求出通解为：y=1+Ce-x。此时，C=ex(y-1)，于是辅助函数就是该任意常数的表达式，即

F(x)=ex[f′(x)-1]

剩下的过程结合已知与第一问，利用罗尔定理可以轻松进行。

2 结论

综上所述，当碰到证明含二阶导数的这样一类中值问题F(ξ,f(ξ),f′(ξ),f″(ξ))=0时，采用逆向思维的思想，从结果出发，先构造微分方程，利用降阶的思想，求出未知函数导数满足的关系式，那么任意常数的表达式就是我们要找的辅助函数。找到辅助函数以后，利用罗尔定理去证明即可。这个过程中辅助函数的构造是重点也是难点[4-5]。文中从两种常见题型出发，详细阐述了构造辅助函数的逆向思维，帮助大家建立解题方法与结构，从而顺利证明这类问题。

教师在给学生讲解这类问题时，通过给出提示、提供线索等手段对学生一步一步进行适当地引导，帮助学生自己找到解题思路或程序。这种教学方式既可以活跃课堂氛围，又可以调动和激励大部分学生的学习积极性[6]。这种数学探究性学习的方式，也打破了传统的学生被动接受知识的状况，有效地发挥了学生主体参与的意识，培养了主动求知精神，提高了学生独立思考判断能力，进一步调动了他们解决问题的积极性，使不同程度的学生在数学学习的实践过程中都能学到数学知识，深刻体悟到其中蕴含的思想方法，也充分体现了数学在培养学生思维能力、启迪智慧、提高创新能力等方面有着举足轻重的作用[7]。