考虑刚度影响的双输入转矩分流式齿轮系统均载特性*
2021-04-09郭文勇韩江桂余平波
魏 维,郭文勇,韩江桂,余平波
(1. 海军工程大学 动力工程学院, 湖北 武汉 430033; 2. 武警海警学院 机电管理系, 浙江 宁波 315800;3. 中国人民解放军61068部队, 陕西 西安 710100)
转矩分流齿轮系统具有重量轻、传递载荷大以及能够降低传动噪声等优点,最早在直升机中得到应用。Rashidi[1]和White[2-3]分别对直升机转矩分流传动系统的动力学特性进行了研究;Krantz[4-5]等对直升机齿轮箱的均载特性以及振动特性进行了研究;White[3]对模型直升机力矩分流传动系统进行了设计分析;Bechhoefer等[6]通过利用多种齿轮分析算法,对转矩分流齿轮箱的性能状态量化方法进行了研究。现代船舶科技的发展对传动系统功率密度提出了更高的要求,由此推动了转矩分流齿轮系统在船舶动力系统中的研究与应用。张婷[7]、董皓[8]以及李楠[9]等分别对转矩分流系统的固有特性和动载系数进行了求解。常乐浩等[10]以船用转矩双分流二级齿轮系统为研究对象,对系统的动态特性进行了求解。现有文献虽然对转矩分流轮系均载特性进行了较多研究,但在联动轴扭转刚度、齿轮支撑刚度等因素对均载特性影响方面研究不足,且尚无文献研究轴位角对系统均载特性的影响,不能为船用转矩分流轮系的设计与应用提供充分的理论支撑。
本文以船用双输入转矩分流齿轮传动系统(以下简称转矩分流轮系)为研究对象,建立考虑时变啮合刚度、时变齿侧间隙等非线性因素的动力学模型,开展联动轴扭转刚度、支撑刚度、输入转速以及轴位角对系统均载特性影响的研究,为船用转矩分流轮系的分析和设计提供理论依据。
1 系统动力学模型
转矩分流轮系三维模型结构如图1所示,其输入端分别与主机的高压输出端和低压输出端相连,系统的动力传递路线自然分为高压侧和低压侧。为了提升传递效率、提高传递功率,高、低压侧分别采用转矩分流形式的二级齿轮传动,来自主机的功率最后通过Ⅱ级小齿轮与Ⅱ级大齿轮的啮合传递到输出轴。
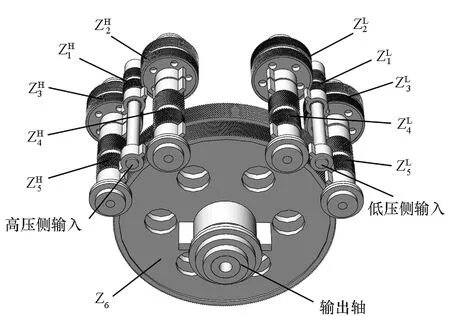
图1 转矩分流轮系模型结构Fig.1 Model structure of torque-spilt gear system
转矩分流轮系动力学模型如图2所示,在建模时假设:轮毂为刚体,轮齿为弹性体;齿轮轴两端的轴承具有相同的参数和动力学特性;组成人字齿轮的两个斜齿轮具有相同的啮合刚度、啮合阻尼以及静态传动误差;考虑传动轴侧扭转变形。本模型中不考虑齿面摩擦以及偏心对系统的影响,同时忽略人字齿轮轴向振动。


图2 转矩分流轮系动力学模型Fig.2 Dynamic model of torque-spilt gear system
综合以上分析,系统的广义位移向量可表示为
(1)
2 系统动力学微分方程
2.1 动态啮合力
随着齿轮的转动以及轴承间隙的变化,齿轮的中心坐标随着时间发生变化进而引起啮合中心距以及啮合角的变化,使得齿侧间隙也处于动态变化中,动态齿侧间隙可表示为
b(t)=2b0+2a0(invα′(t)-invα0)cosα0
(2)
式中,α′(t)=arccos(a0cosα0/a′(t)),b0为初始齿侧间隙,invα=tanα-α,a0、α0为初始安装中心距和压力角,a′、α′为齿轮运行过程中的中心距和压力角。其中动态中心距可表示为
(3)
根据齿侧间隙的分段特性,动态间隙的非线性函数可表示为

(4)
式中,δ(t)为齿轮啮合动态传递误差函数。
齿轮系统受到激励力的作用,在平衡位置做微小振动,将振动状态的x方向的相对位移以及y方向的相对位移转换到啮合线上,如图3所示。
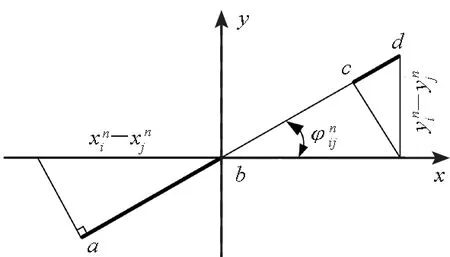
图3 齿轮啮合线相对位移Fig.3 Relative displacement of gear mesh line

(5)

考虑传动系统的齿侧间隙,各齿轮间动态啮合力可表示为
(6)

由于齿轮啮合刚度随着齿轮的转动具有明显的周期性,为了后续计算的方便,斜齿轮法向综合啮合刚度可表示为Fourier级数的形式
(7)
式中,k0为平均啮合刚度,k0=(0.75εα+0.25)kp,且有
(8)
(9)
其中:εα为端面重合度;ωm为啮合频率;kp=1/q为单对齿啮合刚度,q的计算公式为
(10)
式中:zv1、zv2分别为大、小齿轮的当量齿数;zv=z/cos3β,其中β为齿轮螺旋角。
2.2 系统微分方程
考虑到传动系统中高压侧与低压侧结构形式相对称,因此微分方程相同,本文只对单侧传动系统的微分方程进行推导。根据对每个齿轮受力状态进行的分析,再运用拉格朗日方程,得到各齿轮副的运动微分方程为
(11)
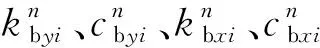
2.3 联动轴扭转刚度及阻尼计算
将联动轴简化为理想轴来处理,考虑其扭转变形以及弯曲变形,不计联动轴的质量。联动轴的刚度计算模型如图4所示。
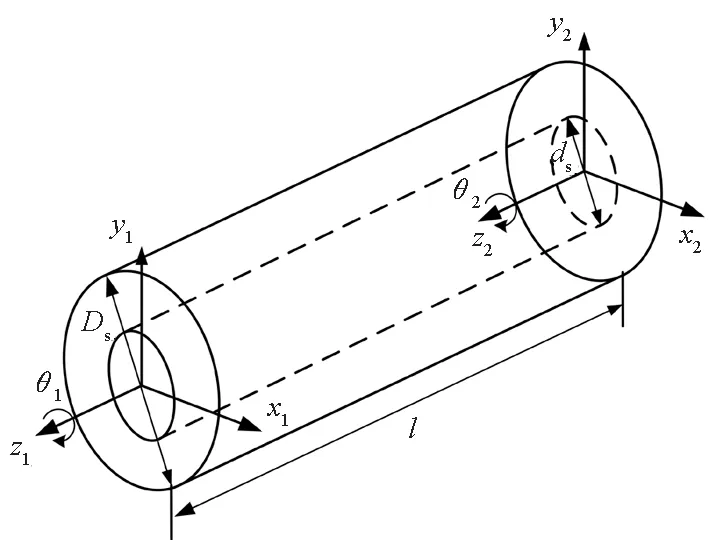
图4 联动轴刚度计算模型Fig.4 Calculation model of linkage shaft
图4中,Ds和ds分别为联动轴的外径和内径,l为联动轴长度,联动轴两端的自由度分别为{x1,y1,θ1}和{x2,y2,θ2}。根据材料力学的相关知识,联动轴的扭转刚度、弯曲刚度的计算公式为
(12)
式中:E和G分别是联动轴材料的杨氏弹性模量以及剪切弹性模量;Ix、Iy和J分别是轴截面关于x、y轴的惯性矩以及截面的极惯性矩,计算公式为
(13)
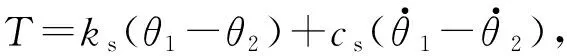
(14)
式中,ξs为相对阻尼比系数,I1、I2分别为联动轴两端截面相对于中心的极惯性矩。
2.4 齿轮啮合线夹角计算
齿轮啮合线夹角计算模型如图5所示。图中用a1表示高压侧两转矩分流轮与Ⅱ级大齿轮中心连线的夹角,即线段O35O6与O24O6之间的夹角;用a2表示高压侧Ⅰ级小齿轮、Ⅱ级大齿轮中心连线与竖直方向的夹角,即线段O1O6与y方向的夹角;用a3表示高压侧两转矩分流轮与Ⅰ级小齿轮中心连线的夹角,即线段O1O24和O1O35之间的夹角。考虑到高、低压侧齿轮传动组各齿轮位置沿中轴线对称,所以上述位置角低压侧与高压侧相同,此处不再论述。根据几何关系,经过推导可以得到各齿轮啮合线与x轴正向的夹角为
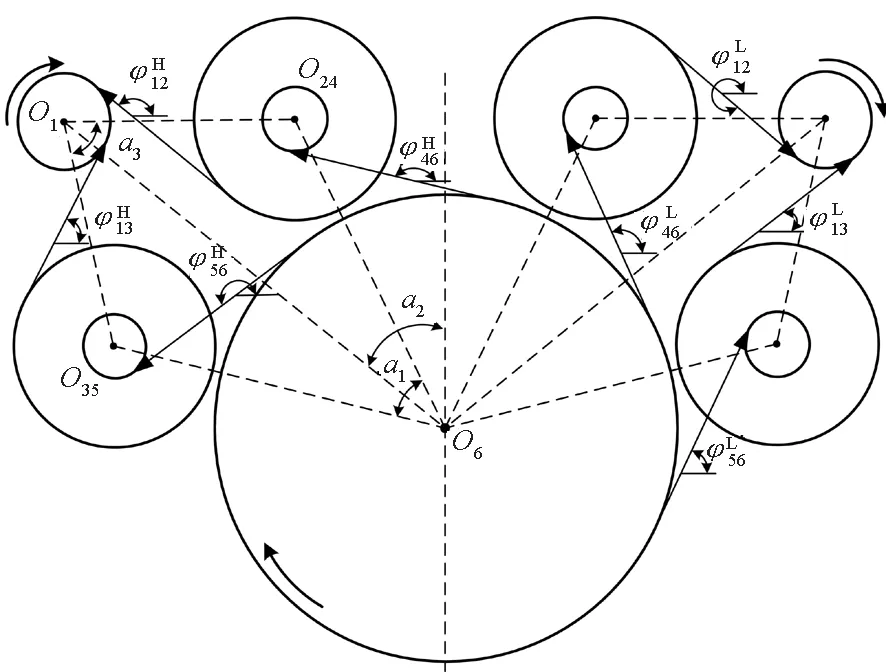
图5 齿轮啮合线夹角计算模型Fig.5 Calculation model of gear meshing angle

(15)
(16)
其中:αti为齿轮的端面压力角;a1、a2如图5中所标注,其大小决定了高、低压侧齿轮组的位置。根据几何关系可知由a1能够得到a3,其计算公式为
(17)
2.5 系统均载系数计算
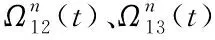
(18)
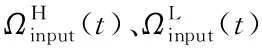
(19)
3 系统均载特性分析
转矩分流轮系均载特性的好坏直接决定了船舶动力系统的工作性能,因此本文在集中质量数学模型的基础上对其进行数值仿真,以研究联动轴扭转刚度、支撑刚度、输入转速以及轴位角对系统均载特性的影响。本文采用4阶定步长Runge-Kutta算法对系统微分方程进行求解。系统参数如表1所示,设高压侧输入转速为3 000 r/min。
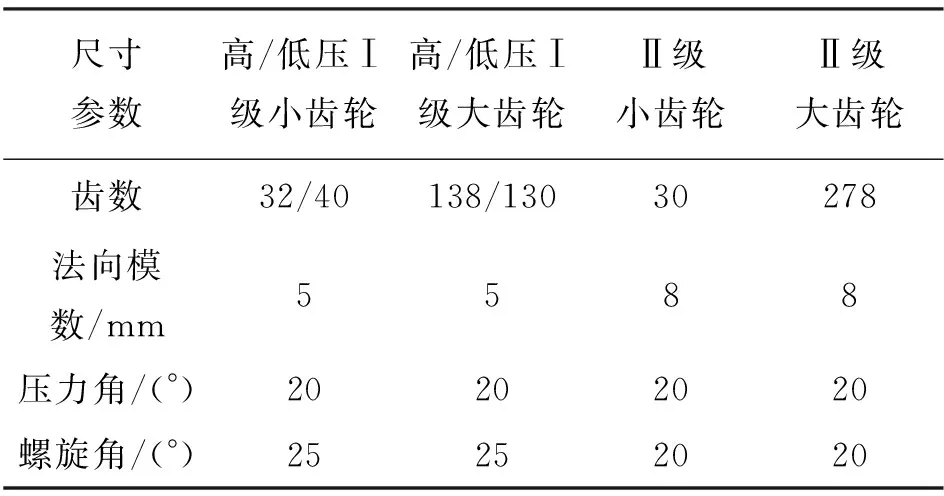
表1 齿轮结构参数Tab.1 Parameters of gears
将联动轴的扭转刚度从105N·m/rad增加至107N·m/rad,分析扭转刚度对转矩分流系统均载系数的影响规律,计算结果如图6所示。由图中曲线可以看出,在所取扭转刚度范围内,系统输入端、输出端均载系数都随着扭转刚度的增加而增加。当扭转刚度小于106N·m/rad时,均载系数对扭转刚度的变化较为敏感;当扭转刚度大于106N·m/rad时,均载系数的变化趋于平缓。由曲线变化规律可知,通过减小联动轴的扭转刚度,可以降低均载系数进而提升系统的均载特性。这是因为当扭转刚度较小时,联动轴可通过较大的扭转变形吸收部分齿轮啮合引发的冲击,进而使得传递的力矩趋于平稳。

图6 系统随联动轴扭转刚度变化的振动响应Fig.6 Influence on load sharing coefficients with the changes of torsional stiffness of the linkage shaft
令转矩分流系统输出轴y向支撑刚度从107N/m增加至109N/m,对其进行数值计算,分析支撑刚度对系统均载特性的影响,计算结果如图7所示。由图中曲线可以看出,随着支撑刚度的增加,系统输入端、输出端均载系数呈现先快速下降后平缓的变化趋势。当支撑刚度小于108N/m时,支撑刚度对均载系数的影响较大;当支撑刚度大于108N/m时,增加支撑刚度对系统均载系数影响不大。由上可知,在一定范围内增加输出端支撑刚度有助于改善系统的均载特性。

图7 系统输出轴支撑刚度对均载系数的影响Fig.7 Influence on load sharing coefficients with the changes of support stiffness of the output shaft
令系统输入转速从1 000 r/min增加至6 000 r/min,对系统模型进行数值计算,研究在不同转速下转矩分流系统的均载系数变化规律,计算结果如图8所示。由图中曲线可以看出,系统均载系数在不同转速下波动变化,输出端均载系数大于输入端均载系数,在4 100~4 400 r/min的输入转速区间出现了均载系数峰值,说明此时系统的啮合频率与固有频率相近从而引发了谐振,其中高、低压输入端均载曲线出现了两个谐振峰值,说明输入端在此处有相邻的两阶局部模态频率。

图8 系统输入转速变化对均载系数的影响Fig.8 Influence on load sharing coefficients with the changes of input speed
轴位角a1、a2是决定转矩分流轮系结构布局的两个重要的参数,在一定范围内改变轴位角的数值,分析其变化对系统均载系数的影响。以齿轮间发生干涉为边界条件,可计算得到a1的取值区间为[33.5°,41.2°],在实际中a1的取值范围应小于上述极限区间,同时对a1的边界值取整,可得a1的计算取值区间为[34°,41°]。同理可得a2可取的最小值为37.9°,设其计算取值区间为[38°,90°]。计算所得均载系数结果如图9所示。
由图9(a)中均载系数分布曲面可以看出,轴位角一定时,均载系数输出端大于高压输入端,高压输入端大于低压输入端,这与前述分析结果相
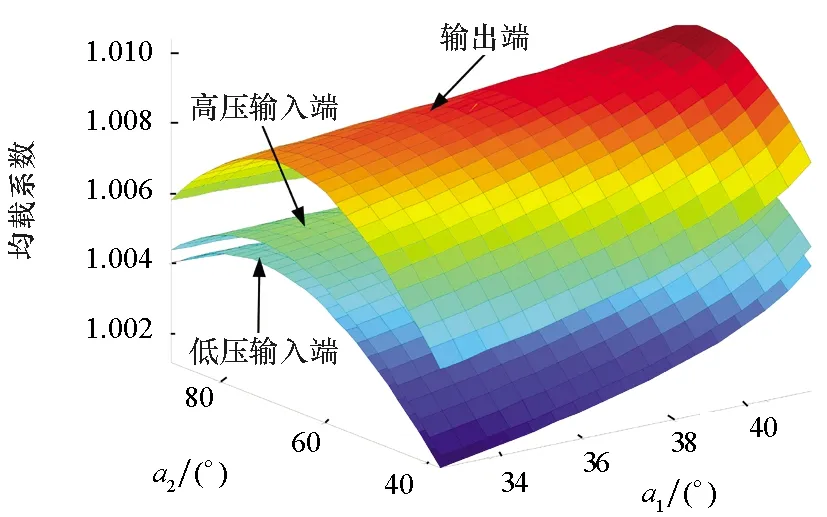
(a) 均载系数三维云图(a) Three-dimensional diagram of load sharing coefficient
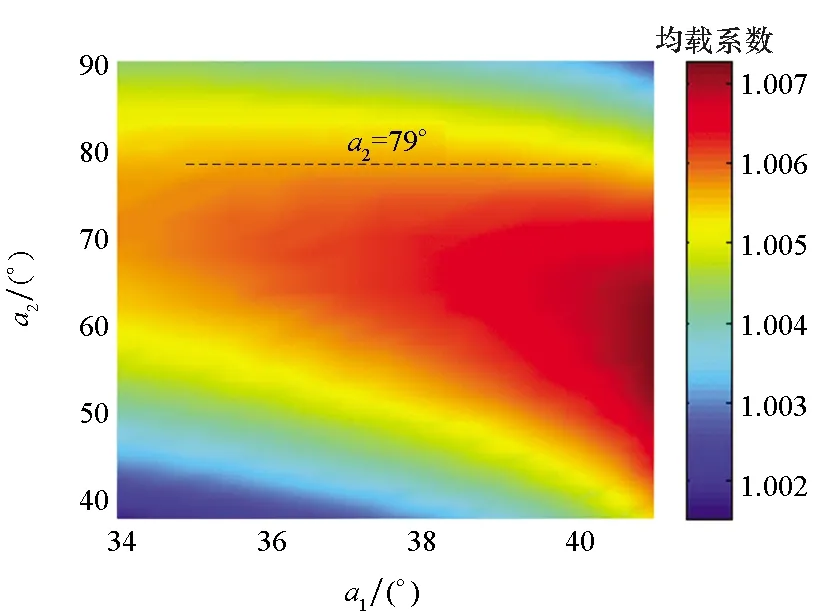
(b) 高压输入端均载系数(b) Load sharing coefficient of high pressure input end

(c) 低压输入端均载系数(c) Load sharing coefficient of low pressure input end

(d) 输出端均载系数(d) Load sharing coefficient of output end图9 轴位角变化对均载系数的影响Fig.9 Influence on load sharing coefficients with the changes of position angle
一致。图9(b)~(d)为均载系数随轴位角变化的二维云图,由图可直观地看出不同轴位角组合时系统均载系数的分布情况。输入、输出端均载系数的变化规律相同;当a1=34°、a2=38°时均载系数最小,当a1=41°、a2为60°左右时均载系数最大。均载系数随a1变化的规律与a2的值有关,分界值出现在a2为79°左右,此时均载系数几乎不受a1变化的影响;当a2小于此分界值时,均载系数随a1的增加而增加;反之均载系数随a1的增加而减小。a1一定时,均载系数随a2的增加呈现先增加后减小的趋势。由上述分析可知,在保证齿轮不发生干涉的前提下尽可能减小轴位角可以提高系统的均载性能。
4 实验验证
对某型船用功率分支齿轮系统进行实验,测试不同工况下齿轮系统的振动响应,将实验结果与理论计算结果进行对比,以验证本文齿轮系统动力学建模的正确性。
4.1 实验装置
齿轮系统实验装置如图10所示,图中1为电动机,2为齿轮增速箱,由电动机、增速箱以及中间的联轴器共同组成了试验系统的输入单元;3为船用双输入功率分支试验齿轮箱;4为支持轴承,5是齿轮增速箱,6是测功器,这3个装置及其中间的联轴器共同组成了试验系统的负载单元。
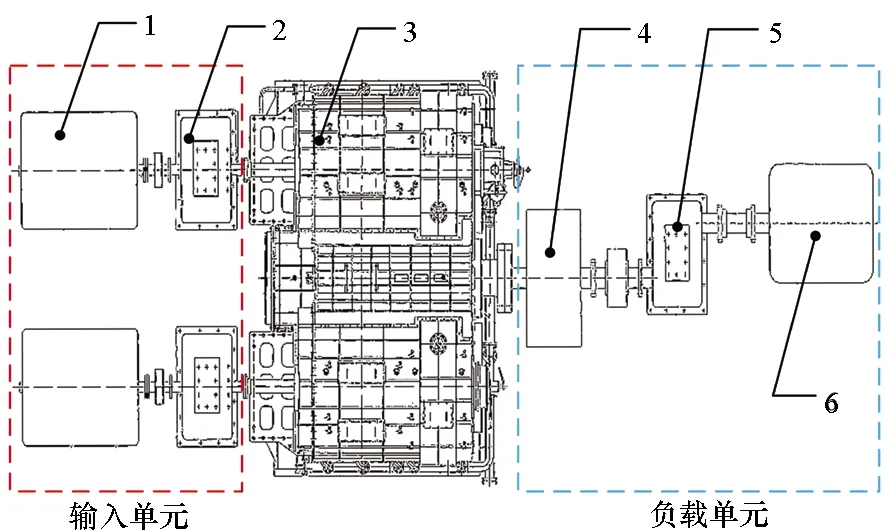
图10 功率分支齿轮系统实验装置布置Fig.10 Arrangement diagram of power-split gear system
4.2 测试原理及实验工况
在实验前对整个测试系统进行校准,包括各个加速度传感器、信号放大器以及数据自动采集处理系统。将各个测点打磨平整并做好标记,传感器磁性底座放于各测点上。测试时,将由BK4384压电加速度传感器测得的振动信号经DLF-8电荷电压滤波积分放大器放大,并积分变为振动信号后进入INV306U-5260智能信号采集处理分析仪进行采集,最终数据进入信号分析系统进行分析。图11为齿轮实验系统测试框图。
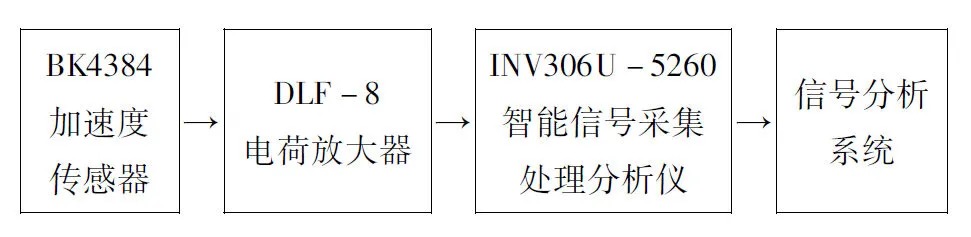
图11 齿轮振动分析系统框图Fig.11 Structure of vibration test system
齿轮系统测试运行工况如表2所示。输入转速分别为2 860 r/min、4 090 r/min以及6 650 r/min,对应的负荷分别为350 kW、1 100 kW以及3 000 kW。
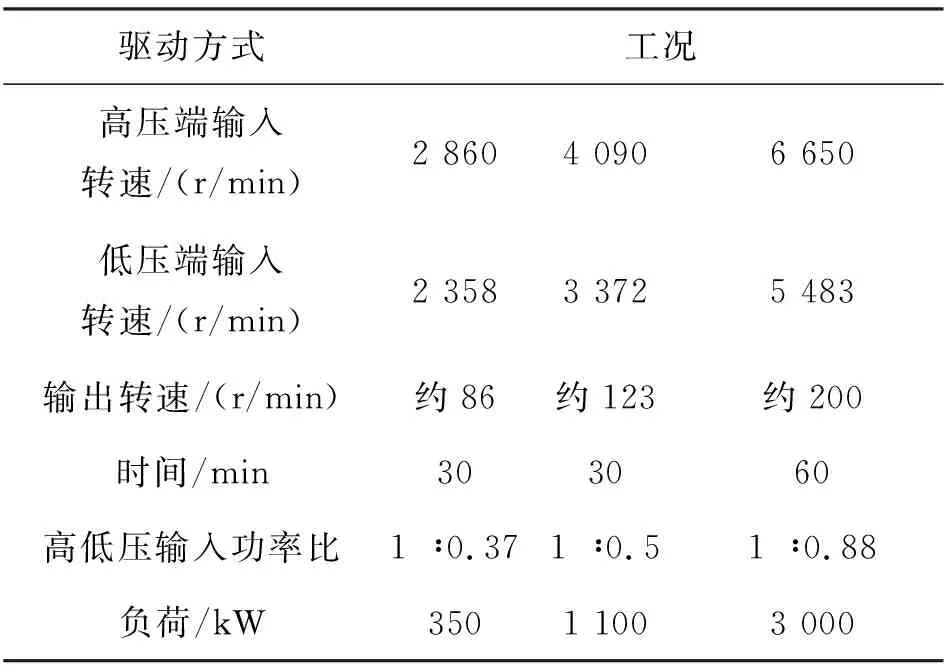
表2 系统测试运行工况Tab.2 Operation conditions of test system
4.3 实验结果及分析
对系统高压端输入转速进行设置,令nin分别为2 860 r/min和4 090 r/min,对应的负载功率Pload分别为350 kW和1 100 kW,取输出齿轮轴承处测点竖直方向振动加速度数据,经FFT变换为频域信号后与理论计算结果进行对比,如图12所示。
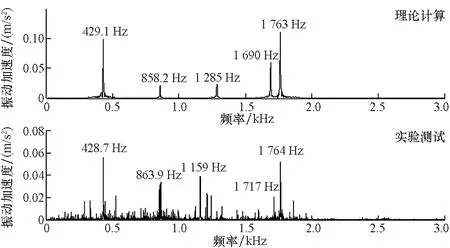
(a) nin=2 860 r/min,Pload=350 kW
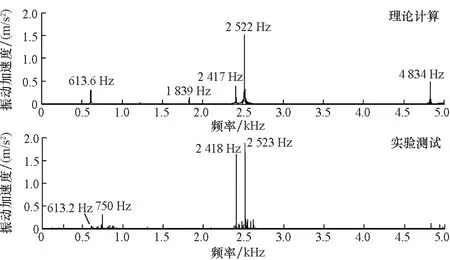
(b) nin=4 090 r/min,Pload=1 100 kW图12 不同工况下理论计算结果与实验测试结果对比Fig.12 Comparison between theoretical calculation and experimental test under different condition
由图12(a)可知,当输入转速为2 860 r/min时,实验测试频谱的主要成分为二级啮合频率428.7 Hz及其二倍频863.9 Hz、高压一级啮合频率1 764 Hz以及低压一级啮合频率1 717Hz,上述频谱理论计算的结果为429.1 Hz、858.2 Hz、1 763 Hz以及1 690 Hz,理论计算结果与实验测试结果基本相同。在图12(b)中,当输入转速为4 090 r/min时,高、低压一级啮合频率的理论值分别为2 522 Hz和2 417 Hz,对应的幅值为1.6 m/s2和0.45 m/s2;实验结果的频率为2 523 Hz和2 418 Hz,对应的幅值分别为1.88 m/s2和1.72 m/s2。理论计算的二级啮合频率及其幅值为613.6 Hz和0.42 m/s2,实验结果与理论计算结果吻合得较好。
综上所述,理论计算结果与实验测试结果在频率和幅值上基本保持一致,可以说明本文所建齿轮系统动力学模型的正确性和分析方法的合理性。在部分频率上的幅值存在一定的偏差,其原因有以下几个方面:理论计算时没有考虑齿轮箱箱体及其辅助装置的影响;在建模时没有考虑齿轮的制造、安装、偏心等因素对系统的影响;在进行测量时也会带来一定的误差。
5 结论
本文建立了双输入转矩分流齿轮系统的非线性动力学模型,以系统输入、输出端的均载特性为研究目标,分别计算了系统随联动轴扭转刚度、输出轴支撑刚度、输入转速以及轴位角变化的均载系数,通过对结果的分析可得以下结论:
1)输出端的均载系数大于输入端的均载系数,高压输入端的均载系数大于低压输入端的均载系数。
2)系统输入端、输出端均载系数都随着联动轴扭转刚度的增加而增加,当扭转刚度大于106N·m/rad时,其变化对均载系数的影响较小。
3)系统输入端、输出端均载系数随着支撑刚度的增加呈现先下降后平缓的变化趋势。当支撑刚度小于108N/m时,支撑刚度对均载系数的影响较大;当支撑刚度大于108N/m时,支撑刚度对系统均载系数影响不大。
4)系统均载系数在不同转速下呈现波动变化,在4 100~4 400 r/min输入转速区间出现了均载系数的峰值,说明此时系统发生了谐振,实际系统中应避开此工作转速区间。
5)轴位角a2的值会影响均载系数随a1变化的规律,在a2为79°左右时会出现临界状态,此时均载系数几乎不受a1变化的影响;当a2小于此分界值时,均载系数随a1的增加而增加;反之均载系数随a1的增加而减小。a1一定时,均载系数随a2的增加呈现先增加后减小的趋势。
6)通过实验结果与理论计算的对比,两者结果相吻合,验证了本文所建模型的正确性和分析方法的合理性。
