加权随机模拟的时变可靠性分析方法*

袁修开，郑振轩，罗冬秀

(厦门大学 航空航天学院， 福建 厦门 361005)

在工程系统的可靠性分析中，时变不确定性广泛存在，如材料强度会随着工作时间发生变化。因此，系统性能的极限状态函数是一个复杂的随机过程。关于时变可靠性分析问题的研究早在20世纪40年代就开始进行了，目前的时变可靠性研究方法主要可归纳为三大类，分别为跨越率法[1-7]、极值方法[8-16]以及复合极限状态函数求解法[17-21]等。

跨越率法是在20世纪40年代Rice提出了首次超越概率计算公式[1]。之后，Coleman给出了关于首次超越概率的可靠性分析方法[2]。Crandall又将数值模拟的方法引入跨越率法计算之中[3]。在近几年，Hu和Du提出了一种联合跨越率的方法求解时变可靠性问题[4]。Andrieu-Renaud等基于跨越率法提出一种计算方法，即PHI2方法[5]。Sudret在PHI2方法的基础上，给出了PHI2方法的近似表达式来求解跨越率[6]。由于在实际工程中一般只能得知不确定性参数的区间范围，故张德权等提出了关于区间的PHI2方法[7]。但跨越率法依赖于穿越过程假设，这会带来精度上的误差。

极值方法主要分为两种，一种是将随机过程近似为极值分布[8-10]，即对随机过程在一段时间内的极大值进行统计，获取极大值的统计参数，之后再运用静态可靠性分析方法对其进行求解。如贡金鑫等[8]提出考虑抗力变化的结构可靠度分析方法，其将随机过程近似为极值Ⅰ型分布，推导出关于时变可靠性的近似表达式。王新刚等[9]同样也是采用将随机过程近似为极值Ⅰ型分布进行求解。黄新萍等[10]基于贡金鑫的方法对非线性结构进行了时变可靠性分析。Li等[11-12]同样也是通过将随机过程转化为极值问题来对时变可靠性进行求解。Hu和Du[13]提出一种通过统计随机过程的极值分布规律，得出极值的分布参数，从而将时变可靠性问题转化为静态可靠性问题进行求解。近年来，有另外一种关于极值的方法是建立代理模型[14-16]。通过建立输入随机变量(随机过程)与输出响应极大值之间的代理模型来对时变可靠性进行求解。如Zhang等[16]通过将随机过程离散成随机变量，计算出结构响应并且取其极大值，建立起输入参数和响应极大值之间的代理模型，最后通过一次二阶矩进行计算。

复合极限状态函数求解法[17-22]是首先将随机过程离散化[20]，之后再运用时变可靠性中的瞬时失效概率和串联系统可靠性将时变可靠性问题转为静态可靠性问题求解。Zissimos等[17-18]通过运用全概率定理和复合极限状态的概念，针对输入随机变量和输入随机过程的时变可靠性分析，提出了一种新的可靠性分析方法。Li等[22]将单响应的时变可靠性通过复合极限状态函数法转化为多响应的静态可靠性分析，再运用GSS(generalized subset simulation)方法计算得到累积失效概率，最后再通过插值的方法得到累积失效概率曲线。

本文在极值方法的基础上，结合加权思想[23-25]，提出基于加权思想的时变可靠性分析方法，分别为加权蒙特卡洛(Weighted Monte Carlo Simulation， WMCS)算法和加权重要抽样(Weighted Importance Sampling， WIS)算法，所提方法通过一次可靠性分析即可将时变失效概率表达成样本的函数形式，从而大大提高时变可靠性分析效率。通过算例分析，将其结果与直接蒙特卡洛仿真的真实值对比来验证基于加权思想的可靠性分析方法的准确性和高效性。

1 时变可靠性分析模型

在机械结构的可靠性分析中，依据应力-强度理论，时变机械结构响应Z(t)的功能函数(亦称为极限状态函数)g(·),形式可定义为：

Z(t)=g(R,Q(t),G)

(1)

其中：G是固定载荷或随机载荷；Q(t)是可变载荷的随机过程，为时间t的函数；R是机械结构的抗力值，本文中假设其为随机变量。在设计基准期T内的累积失效概率可以表示为：

PF(T)={g(R,Q(t),G)≤0,∃t∈[0,T]}

(2)

其中，∃表示“至少存在一个”。

时变可靠性的极值方法是通过时间离散后，采用极值分布来将随机过程等效为随机变量，从而将时变问题转化成静态可靠性问题。以Q(t)转化为例，首先将设计基准期T分为m个时段，每个时段为δ=T/m，则将Q(t)离散为m个参数为αδ和μδ的极值Ⅰ型分布随机变量Qi(i=1,…,m)，然后求解Qi的极值，QT=max(Qi)，其对应的分布参数为：

(3)

则式(2)的时变累积失效概率可转化为：

PF(T)={g(R,QT,G)≤0}

(4)

更进一步，任意时间段[0,t]下的时变累积失效概率函数为：

PF(t)={g(R,Qt,G)≤0}

(5)

其中，Qt为[0,t]上Qi的极值。可看出式(4)中的PF(T)为t=T时的累积失效概率。若要求解不同时间段内的失效概率，即失效概率与时间的函数关系，则一般需重复多次进行可靠性分析。

本文提出基于加权思想的时变可靠性分析方法。该方法通过一次常规可靠性分析模拟，将时变失效概率函数表达成样本的加权函数形式，即可高效得到不同时段内的时变可靠性结果。

2 基于加权思想的可靠性分析方法

本文将采用加权思想，结合蒙特卡洛法和重要抽样法提出加权蒙特卡洛法和加权重要抽样法高效求解时变可靠性问题，所提方法的优势在于仅需一次可靠性分析。

2.1 加权蒙特卡洛法

加权思想期望用一次可靠性分析来推断不同时间段的失效概率，从而避免重复进行可靠性分析。

首先，构造一个基本随机变量x=[R,Qt,G]的“辅助概率密度函数”f(x|t0)，其对应某一时刻t0变量的分布。式(5)的时变累积失效概率函数可转化为：

=Et0[IF(x)rMCS(x,t,t0)]

(6)

其中：IF(·)为系统失效的指数函数；f(x|t)为对应任意t∈[0,T]时刻的变量分布；rMCS为“权重因子”，为概率密度函数的比值，即

(7)

通过式(6)可以看出t时刻的失效概率可以表示为该时刻权重因子在概率密度函数f(x|t0)的期望形式，时变失效概率的无偏估计可以表示为：

(8)

其中，x(j)为采用f(x|t0)抽取的样本。进一步地，可得到失效概率函数估计的方差：

(9)

由于式(8)中对于不同的时间t用的是同一组随机样本x(j)(j=1,2,…,N)(来自f(x|t0))和相同的指示函数IF(x(j))，因此无须重新调用功能函数。在估计过程中，需要重复计算的仅是各时刻下的权重系数，而权重系数只是概率密度函数的比值，并不需要结构系统的分析，无须太大的计算代价，因此所提方法可以大大减小时变可靠性分析的工作量，提高计算效率。

前面提到f(x|t0)是辅助概率密度函数，它所产生的样本将用于不同时刻失效概率的估计，因此需合理选择f(x|t0)，尽可能地考虑所有时刻情况。在构建辅助概率密度函数时，首先把与时间无关的随机变量归为一组，记为xr=[x1,x2,…,xnr]，其余为xs=[x1,x2,…,xns]，则辅助概率密度函数可以表示为：

f(x|t0)=f(xr|θt0)f(xs)

(10)

其中，θt0表示与时间相关的随机变量的分布参数在某一时刻t0的取值，如一般可以取t0=T/2。

2.2 加权重要抽样法

加权蒙特卡洛法仍然受限于蒙特卡洛法的效率，为了提高计算效率，本文进一步提出加权重要抽样法。采用加权的思想，可以将重要抽样用于时变可靠性分析。

构造一个“全局”重要抽样密度函数H(x)，式(5)的失效概率函数可以表示为：

(11)

在抽取H(x)样本x(j)(j=1,2,…,N)后，失效概率函数的无偏估计可表示为：

(12)

类似地，可得到失效概率函数估计的方差：

(13)

本文在构建H(x)时借鉴基于设计点的构造方法。首先计算得到设计点x*(如可采用改进一次二阶矩法)，然后选取正态分布密度作为抽样密度，以设计点x*作为抽样密度中心，则H(x)可以表示为：

H(x)=φ(x|x*,σH)

(14)

其中，φ(·)表示正态概率密度函数，σH表示随机变量的标准差。

3 数值算例分析

3.1 管状悬臂梁

算例来自参考文献[10]，图1为一管状悬臂梁，结构基本参数与所受外力情况见表1，预期工作时间为10 a。其中承受外载P、F及U均为随机变量，Q(t)为随机过程，这里给出其在10 a内的极值QT=max(Qi)的分布。其他参数为确定值，即L1=120 mm，L2=60 mm,θ1=5°,θ2=10°,功能函数定义为强度R与固定端下表面最大应力值之差，即

G(x,t)=R-σmax(x,t)

(15)

图1 管状悬臂梁示意图Fig.1 Tubular cantilever beam

表1 管状悬臂梁结构随机变量分布Tab.1 Random variable distribution of tubular cantilever beam structure

其中σmax(x)可通过以下计算获得：

(16)

(17)

(18)

计算该悬臂梁在工作期内的失效概率随时间变化的函数。

采用本文所提方法来求解结构时变可靠性，加权蒙特卡洛法的“辅助概率密度函数”f(x|t0)在t0为第5 a时构造，对应的变量均值为μx=[440,6.5,22,90,42,5,2.302]。加权重要抽样法中“全局”重要抽样密度函数H(x)为在上述均值点下计算出设计点x*=[245,6.948,2.235,90.04,4.19,5.0,2.435]后进行构建。

加权蒙特卡洛抽样105次，加权重要抽样20+103次(其中采用改进一次二阶矩方法求解设计点调用极限状态方程20次)。直接蒙特卡洛法对10个时间点进行计算，每个时间点抽取106个样本点，共调用功能函数10×106次，作为精确结果进行对比。各方法结果如图2所示(其中N为样本数)。由图2可以看出：该悬臂梁失效概率随时间单调递增，所提方法结果都接近于真实值。表2给出了所提两种方法对应的估计值的误差及变异系数。由此可看出，加权方法只需一次分析，具有较高的效率。进一步地，加权重要抽样法比加权蒙特卡洛法的效率更高。

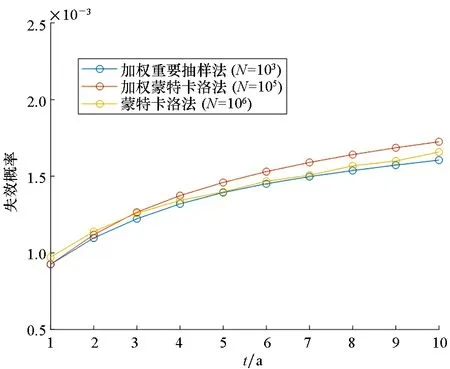
图2 管状悬臂梁1～10 a失效概率图(取t0=5)Fig.2 Failure probability diagram of tubular cantilever beam in 1～10 years(t0=5)

表2 管状悬臂梁1～10 a的失效概率(t0=5)Tab.2 Failure probability of tubular cantilever beams from 1 to 10 years (t0=5)

其次，为了进一步考察方法的稳健性，选取不同的t0，分别再用加权蒙特卡洛法和加权重要抽样法进行分析，结果如图3所示。由图3可以看出，两种加权方法都获得了较为满意的结果。

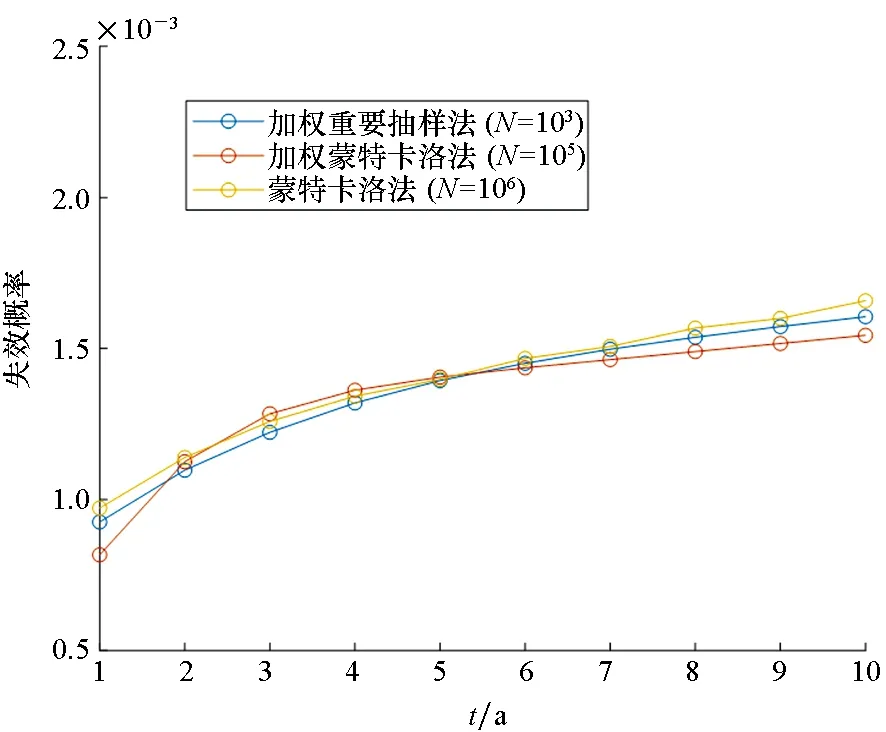
图3 管状悬臂梁1～10 a失效概率图(取t0=1)Fig.3 Failure probability diagram of tubular cantilever beam in 1～10 years(t0=1)

3.2 十杆桁架

图4所示为十杆桁架结构，左端是固定端，各杆的截面积分别为A1～A10，其中1、2、3、4、5和6号杆长度为L；弹性模量为E。该桁架承受3个外载荷，其中F1、F3为随机变量载荷，F2(t)为随机过程载荷，其在使用期限T为10 a的极值F2T的分布列于表3中。要求节点2处的竖直方向位移在使用期限T为10 a内且不得大于允许值d，计算该桁架在使用期限内的失效概率随时间变化的函数。

图4 十杆桁架结构Fig.4 Ten-bar truss structure

表3 十杆桁架随机变量分布Tab 3 Distribution information of ten-bar truss random variable

由题意可知，十杆桁架的功能函数为：

G(t)=d-dy(t)

(19)

其中，dy(t)表示t时刻下2点位置的实际竖直方向位移，可以通过下列公式求得。

(20)

(21)

(22)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

采用本文加权方法来进行分析，其中取t0为10 a。加权蒙特卡洛法的“辅助概率密度函数”f(x|t0)的均值为μx=[0.004,…,0.004, 9.1,70, 12, 20, 8, 0.02]。构造的“全局”重要抽样密度函数H(x)为在设计点x*=[0.004,…，0.004,9.405，67.49，12.08，20.67，7.97，0.02]下构造。

采用所提方法分析得到十杆桁架的失效概率结果如图5和表4所示。直接MCS方法抽取10×106个样本点计算获得的结果作为精确结果。WMCS抽取105和WIS抽取103个样本点。从图5可看出，失效概率随时间增长逐渐增大，均得到较为精确的结果，证实了所提加权方法的正确性。结合表4可以看出，加权方法具有较高的效率和精度。

图5 十杆桁架失效概率Fig.5 Failure probability diagram of ten-bar truss

表4 十杆桁架1～10 a的失效概率(t0=5)Tab.4 Failure probability of ten-bar truss from 1 to 10 years(t0=5)

4 结论

本文针对随机模拟法在时变可靠性分析中计算效率低的问题，在极值方法的基础上结合加权思想，提出了加权蒙特卡洛方法和加权重要抽样方法。所提方法仅需一次常规可靠性分析模拟，即可得到时变失效概率函数结果，大大提升了分析的效率。对文中两个算例进行了验证。算例分析结果表明，加权方法能够在一次可靠性分析下，得到较为满意的可靠性结果，且加权重要抽样方法比加权蒙特卡洛方法效率更高。