知识标签网络生成机制研究

韩 仪，冯 鑫，周金连，吴 晔，肖井华

(1. 北京邮电大学理学院 北京 海淀区 100876；2. 燕山大学经济管理学院 河北 秦皇岛 066004；3. 中山大学传播与设计学院 广州 510275；4. 北京师范大学计算传播学研究中心 北京 海淀区 100875)

知识是在社会化合作进程中的产物之一。在线问答社区是知识生成和交流的一种众包平台，用户可以在其中自主互动。以在线问答平台知乎为例，用户可以根据个人认知对问题进行标注。通过出现在同一个问题上的标签之间建立的连接，构建出一个标签的共现网络。标签信息具有可使用性，用其作为导航和推荐能有效挖掘出用户的行为和偏好[1]，提高个性化系统推荐的准确性[2]。标签网络是一种人工知识网络[3]，它反映了现实世界中知识单元间的复杂关系，通过运用网络分析的方法，找出社会知识系统中的一些特征。例如：度比较大的节点代表知识元素的核心，标签网络中的度分布代表社会知识体系中的宏观主题结构等。此外，通过探索标签网络的动态演化机制，也可以进一步发现知识网络生成和演进的规律。

复杂网络的无标度特性，即幂律分布主导着复杂网络，而非度分布的特定平均指标。以往的研究大多使用抽样数据来验证静态标签网络的无标度特性，证明了高频标签相对较少，而低频标签则相反。文献[4]从2004 年-2007 年间用户在Flikr 平台发布的照片中随机抽取了5 200 万张包含了至少一个标签的照片[2]，证明标签频率分布和每张照片的标签数量分布都遵循幂律分布。另外一项研究随机选择了20 万个问题，发现大约50%的问题包含3 个或数量更多的标签[4]。文献[5]对《美国国家科学院院刊》关键词的统计特性和进化性质进行了频率分布、时间缩放行为和衰减因子分析等经验研究，研究显示1991-2006 年间所有关键词出现的频率近似遵循Zipf 定律，指数为0.86。文献[6]从知乎和Quora 社区随机抽取了100 万个问题，观察到问题标签遵循重尾Zipf 分布，其中98%以上的标签(Quora=99.02%，Zhihu=98.43%)出现次数不超过500 次。同时，许多研究采用复杂网络动态建模的方法研究社会标签规模的增长规律。其中，文献[7]在del.icio.us(美味书签)上研究了用户对图书的标注行为，发现在平台的早期，用户的标注行为在一定程度上呈现出随机性。然而，随着时间的推移，标签规模的分布服从Zipf 定律，基于用户标注行为相互模仿机制的模型能很好地解释标签的分布特征。文献[8]以del.ico.us 和BibSonomy 作为数据源，进一步发现标签增长符合Heaps 定律。即随着新标签的增加，系统中不同标签的数量呈指数增长。文献[9]发现已有用户的背景知识可以解释标签增长的Heaps 定律。事实上，Zipf 定律和Heaps 定律并不独立，这两个定律经常同时出现。文献[10]对Zipf 定律和Heaps 定律之间的关系进行了清晰描述，即Heaps 定律是Zipf 定律的衍生现象。这类研究探索了网络动态演化过程，但主要关注的是标签网络的增长规律。

综上所述，现有的标签网络研究还存在两个不足之处：一是大部分的研究使用了抽样数据，而在实际的社会系统和网络中，社会标签的分类具有复杂、随机、数据量巨大等特点，采样数据可能存在样本代表性的问题；二是静态网络只能表示数据采集时间节点时的网络的最终状态，不能反映标签网络的动态演化过程。而文献[11]提出无标度网络的幂律特性可以由以下两种机制产生：其一为增长，即实际的网络并不是静态的、不变的，而是通过不断地加入新的节点进行增长；其二为优先连接，即在添加新节点时，与旧节点的连接不是随机的，而是一个存在优先选择的过程；从而提出了Barbési-Albert 模型(BA 模型)。基于这两种机制，BA 模型可以模拟无标度网络的动态演化，因此被广泛应用于互联网、科学引文网络、短信通信网络、演员合作网络等。自其被提出以来，研究者们陆续在BA 模型基础上提出了许多变种模型，主要是通过增加新影响因素来拟合复杂网络的生成结构和统计特征，其中文献[12]提出可以调整优先链接中节点被选中的概率来控制网络结构；文献[13]则从增加重连功能入手讨论网络变化；文献[14]提出可增加节点老化特性来模拟节点随着“年龄”增长而竞争力下降的情形，此外还有学者增加了复制特性来描述引文网络中多重引用的情形[15]。

上述基于BA 模型的众多衍生研究都表明，BA网络作为一个基础普适性模型意义重大且影响深远，但在描述现实生活中一些具体网络时却不能较好地适配，知乎中的知识标签网络就是一个典型例子，它是一种用户生成的社会化知识标签网络，统计分析结果表明它存在无标度特性，且其在动态演化过程中也有增长和优先连接机制。因此，本文利用BA 模型模拟了标签网络的形成过程。然而，基础BA 模型只反映了复杂网络演化的最基本特征。本文根据知乎平台标签网络演化的特点对模型进行了以下改进：首先，新标签是以用户提出问题的形式生成的，一个问题可以由多个新标签标记，即一次可以在网络中涉及多个标记节点，其中新标记的数量并不一定是一个。其次，在生成连边的过程中，多个标签之间都会产生连边，而不是像传统的BA模型，只在新节点和旧节点之间产生连边。即知乎上问题的产生将改变网络中旧标签的连接状态。因此，本文研究主要涉及两个方面：首先，以知乎平台的数据为基础，验证标签数量的分布特征。然后，通过2011-2018 年共计9 年间年的数据，探索标签网络的动态演化机制，由此探究社会化知识网络的演化规律。

1 数据来源和网络统计描述

在知乎平台上，每个问题都可用多个标签进行标记。由问题标签数据定义的标签网络反映了标签间连接关系，节点代表标签，节点间边代表标签共现关联，即两个标签同时标记某一问题其间会有连边。为了获得标签网络的拓扑特征和时间演化规律，本文使用了完整的知乎数据集，包含问题创建时间和标签，涵盖了2011-2018 年的问题。经过清洗，一共有来自2 034 404 个问题的76 379 个不同标签。图1 绘制了2011-2018 年问题的累计数量和不同标签累计数量的曲线，研究了数据集的拓扑特征和动态演化趋势，找出了数据的分布特征和演化特征，为建立合理模型提供统计支持。对知乎标签被使用次数与排名之间关系进行分析，未呈现幂律关系，故不符合Zif 定律，如图2 所示。再探索不同标签的数量与累积标签使用数间的关系，基本呈现幂律关系，符合Heaps 定律如图3 所示。

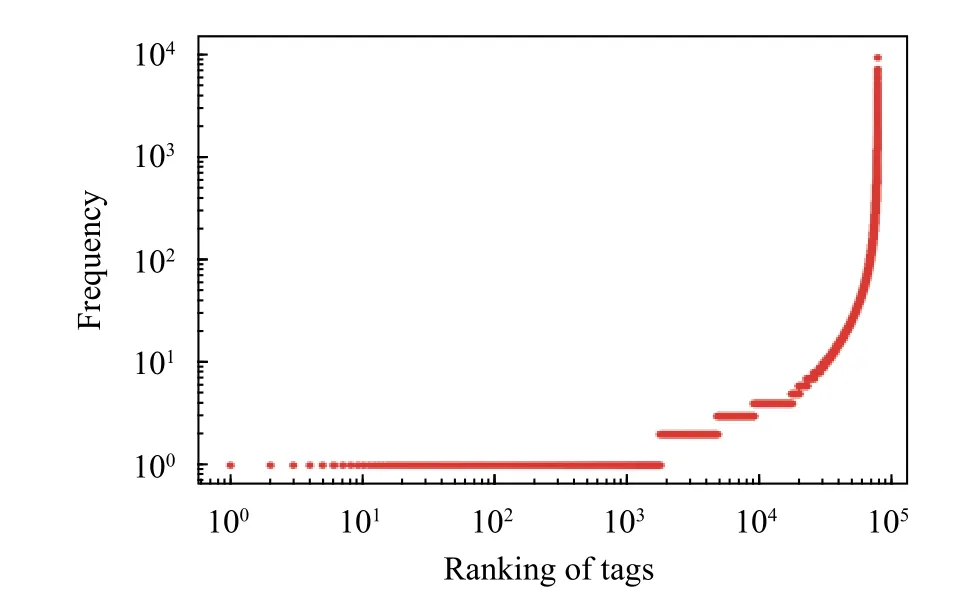
图2 知乎标签被使用次数与排名的的概率分布密度曲线图

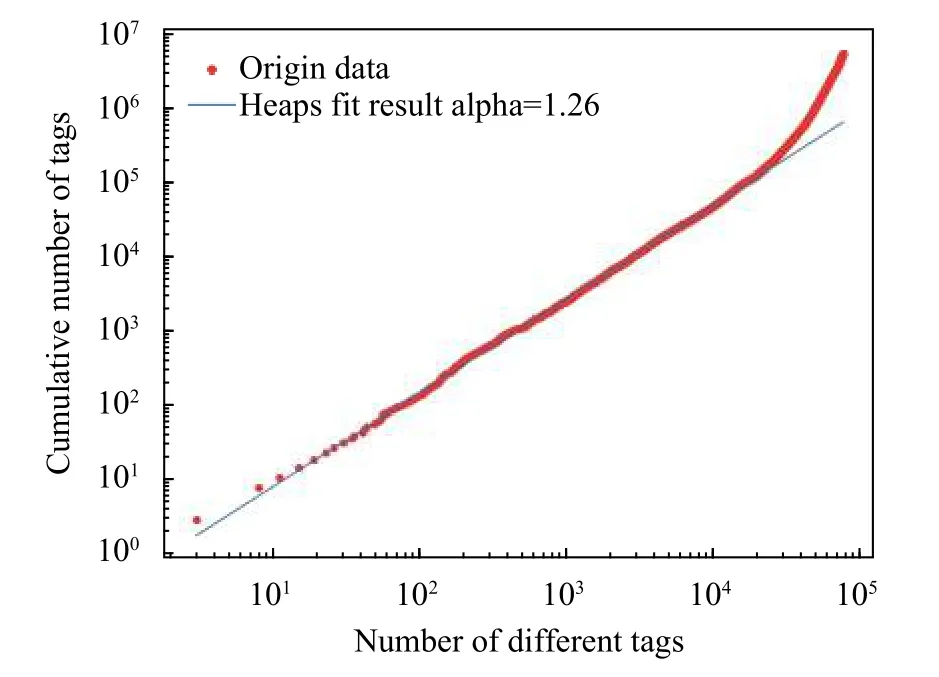
图3 知乎不同标签的数量与累积标签使用数的概率分布密度曲线图

1.1 度分布

度分布是图理论和网络科学中的一个重要概念[16]，反映了网络的结构特点。网络度分布p( k)一般定义为网络中度为k的节点占比。在随机网络中，因其节点之间随机连边，度分布呈现泊松分布。无标度网络是复杂网络中另一种重要类型，其典型特点是网络中大多数节点仅有极少边，而少数节点具有大量边，度分布为幂律分布，许多真实世界网络属于此类，如互联网、金融系统网络及社交网络等。经典的BA 模型用来解释复杂网络的无标度特性。文献[17]在对引文网络的度分布进行研究时指出PR 的引文网络的度分布呈现对数正态分布。而在知乎标签网络中出现了度分布从幂律分布到对数正态分布的演化，幂律分布是具有如下形式的概率分布，

尽管幂律分布很常见，但其检测和描述仍是一个复杂问题，因其分布的尾部通常是波动的。常用幂律分布数据分析方法，如最小二乘拟合，可能会产生明显的估计参数不准确的问题。本文使用python 工具包powerlaw 来解决此问题，它基于文献[18-19]为了对复杂网络的度分布进行分析和拟合而提出的幂律分布分析方法构建。在powerlaw中，可以使用distribution_compare 工具比较不同分布拟合数据的效果，返回值代表了不同的候选分布之间的对数似然比，如果返回值是整数，代表更加符合第一种分布，负数代表更加符合第二种分布。当使用这种方法法对比对数正态分布和stretched exponential 的拟合效果时，返回值是7.435 918 718 516 159 5，代表对数正态分布的拟合效果更好。构建一个全体数据的标签网络如图4所示。蓝色星形标记代表度分布数据，不同颜色实线代表多种拟合方法结果，标签网络的度分布(蓝色星形曲线)明显偏离了幂律分布而更加接近对数正态分布[20]。

图4 2011-2018 年数据构建的标签网络的度分布和拟合结果图

为了探究此现象成因，将数据按照时间以年为单位切片获得8 个子网络，计算其网络参数，可得子网切片的度分布特征。比较不同切片间度分布的差别，观察标签网络演化和发展的动态过程，为后续分析标签网络的度分布与幂律分布的偏差提供线索。

对2011-2018 年各年标签网络度分布进行分析和拟合，如图5 所示，黑色点代表度分布数据，黑色实线代表幂律分布拟合结果，红色实线代表对数正态分布拟合结果，前5 年更接近幂律分布，后3 年逐渐偏离更接近对数正态分布。综上，在用真实知乎数据构建的标签网络中，总体网络的度分布服从对数正态分布，对子网而言网络度分布从幂律分布到对数正态分布的演变趋势。

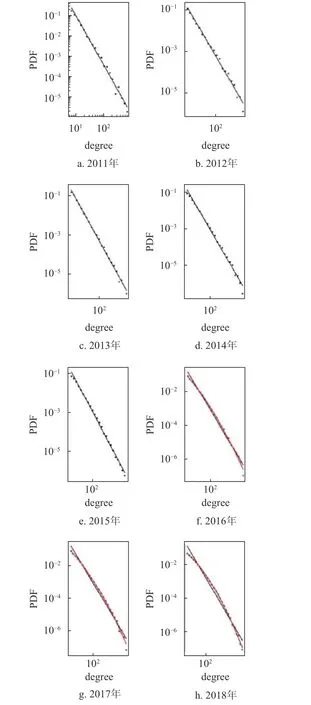
图5 2011-2018 年年度标签网络的度分布与拟合结果图

1.2 幂律分布指数的改变

用幂律分布对8 个年份的子网进行拟合，可以观察到幂律分布的指数变化，如图6a 所示。可以发现知乎标签网络的度分布的幂指数明显小于BA模型所给出的幂指数3，同时可以发现每年的指数总体呈下降趋势，在powerlaw 工具中，当使用幂律分布对结果进行拟合时，会同时给出幂律分布的拟合指数及标准差sigma，当对8 年的度分布数据使用幂律分布拟合时，标准差结果如表1 所示。

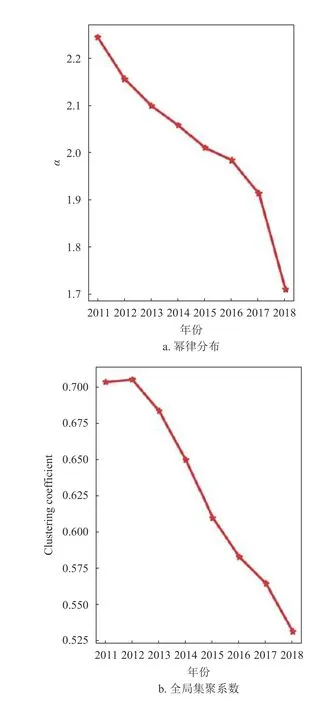
图6 2011-2018 年8 个子网络的幂律分布的指数和全局集聚系数的变化图

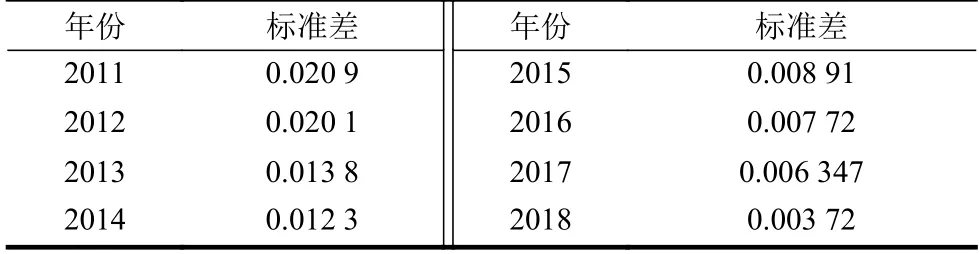
表1 2011-2018 年幂律分布拟合指数的标准差

这说明度值极大的节点的占比逐渐增加，知乎标签网络中度分布的异化情况逐渐减弱，度值的分布相较以往逐渐呈现一定的平均化趋势。

1.3 网络直径的改变

网络中，节点i 和j 的相互通信能力取决于其最短路径，所有节点之间最短路径的最大值定义为网络直径，在一定程度上反映网络连通性。由计算得2011-2018 年的8 个子标签网络直径，如表2 所示知乎标签网络中标签间距离相对较近，尽管随网络规模逐年扩增，其直径依旧基本稳定在8 左右，说明标签间距离并未随网络规模增加而显著增加，也从侧面说明了网络节点间连边较为密集。

表2 2011-2018 年的8 个子标签网络直径

表2 给出的每年的网络直径，对每年计算了一个最短路径等于直径的通路，结果表3 所示。2016年开始，因为网络规模极度增大，计算两两节点对之间的路径算法复杂度很高，计算一个实例需要数十天，因此只计算了2011-2015 年的实例。

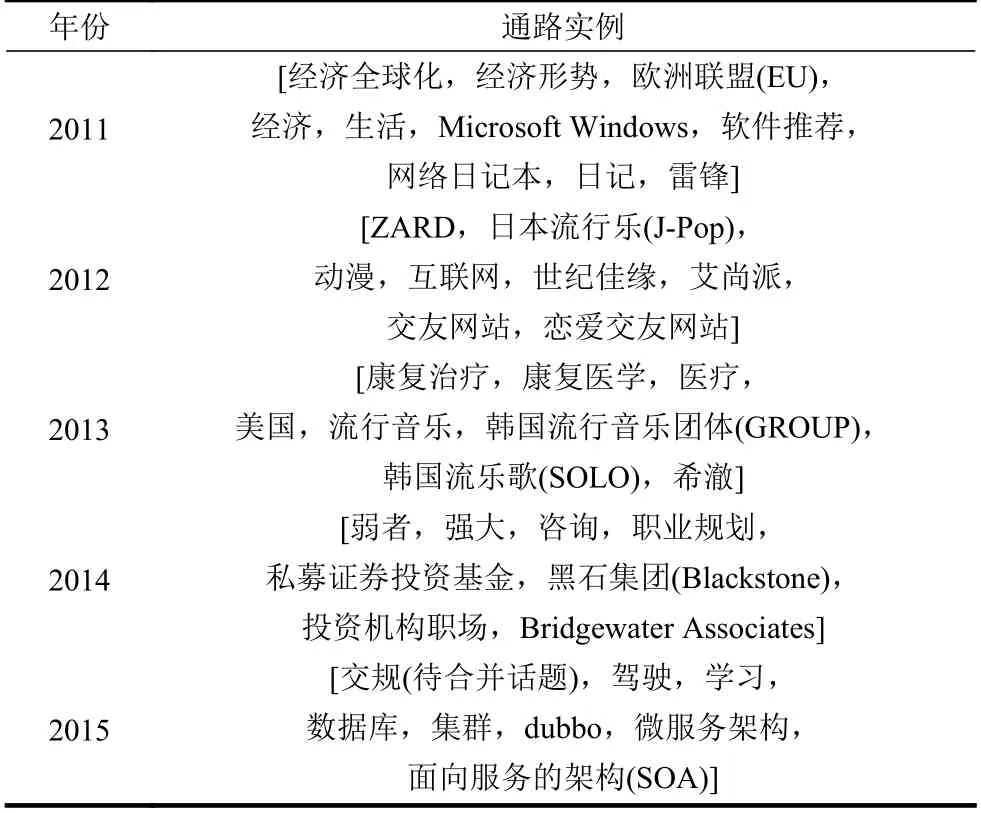
表3 tag 链条示例表

1.4 全局集聚系数

集聚系数常用来描述节点间聚集程度[21]，也可以用于描述节点与邻居的互连程度，可分为全局集聚系数和局部集聚系数两种，前者可评价全网聚集程度，后者可度量每个节点局部聚集程度，如图6b所示，集聚系数较大代表了网络中节点较为密集，其下降代表明随时间推移和网络规模渐增，网络逐渐变得稀疏。知乎标签网络全局聚集系数呈逐年稳步下降趋势。

2 模型与仿真

BA 模型基于增长过程和优先连接机制两个假设，其构建过程为1)增长：从一个初始网络G 开始，一次增加一个新节点；2)连接：每个新节点都会连接到 m个 旧节点上；3)优先连接： m个旧节点的选择标准是度大优先，即一个已有节点i的度是di，则新节点选择它的概率是：

BA 模型给出了无标度网络生成机制简洁且合理的解释，已被成功应用于许多种实际网络，但却只能生成度分布幂指数为3 的网络，故对知乎标签网络而言并不适用。这是因为二者生成机制不相符，且BA 模型难以解释知乎标签网络度分布指数取值以及从幂律分布到对数正态分布的演化。观察知乎标签网络生成过程及参数分布发现：1)每个问题都被一组标签标记；2)在一组标签中，新节点数量并不总是1；3)标记了同一个问题的一组标签之间会产生连边。

因此，基于BA 模型结合知乎标签网络特点，本文提出了知乎标签网络生成模型。相比前者，新模型主要做出了以下调整：1)批量增长(batch growing)：网络生成过程依赖新节点加入，但每次并非单一新节点加入而是有一组节点参与连接，总数为 m，其中新节点占比为p，故调整后新节点增量为mp，旧节点数量是m(1-p)。2)交叉连接(cross linking)：所有 m个节点之间均可能产生连接，即新节点和新节点间、新节点和旧节点间、旧节点和旧节点间均可能产生连接，已有节点间连接关系可能发生改变。对比BA 模型新生边必在新和旧节点间，即边增长只发生于新和旧节点间。3)优先连接：旧节点的选择准则依旧和BA 模型保持一致，度越大的旧节点具有越高优先度。基于上述改进，将新模型命名为“标签网络优先连接模型”。对比知乎标签网络生成过程，从定性角度看，不难发现标签网络有限连接模型与标签批量标记和节点批量新增的机制更加吻合，也更能贴近真实地反映知乎标签网络的生成过程。

2.1 模型仿真

如前所述，BA 模型生成的无标度网络与知乎标签网络的度分布有所差异：1)幂指数不同，前者恒定为3，后者明显小于3 且出现了减小趋势；2)度分布的分布类型发生了变化，后者在后期逐渐呈现了偏离幂律分布的对数正态分布。故为保证标签网络有限连接模式的有效性，它必须能生成度分布满足幂律分布且幂指数可以发生变化的无标度网络，也必须能生成度分布符合对数正态分布的复杂网络。

为了验证模型有效性，通过仿真来研究模型的特点。对于新模型，如果固定 m和p，可以生成一个符合幂律分布的网络，如图7，使用不同的p 值产生的网络的度分布和使用幂律分布拟合的结果。蓝色圆形数据点代表度分布数据，橙色实线代表使用幂律分布拟合的结果。而且幂律分布的指数可以通过p 进行调整，如图8a 所示。此外，如果在网络生成过程中，新节点的比例p 逐渐减小，可以得到一个符合对数正态分布的网络，如图8b 所示。这两个仿真结果表明，本文提出的模型确实可以满足知乎标签网络的度分布特点。图8a 为图7 中幂律分布的指数的变化，图8b 通过在仿真过程中逐渐减小p 值得到的网络的度分布以及使用对数正态分布拟合的结果，其中的蓝色圆形数据点代表度分布数据，橙色实线代表使用对数正态分布拟合的结果。

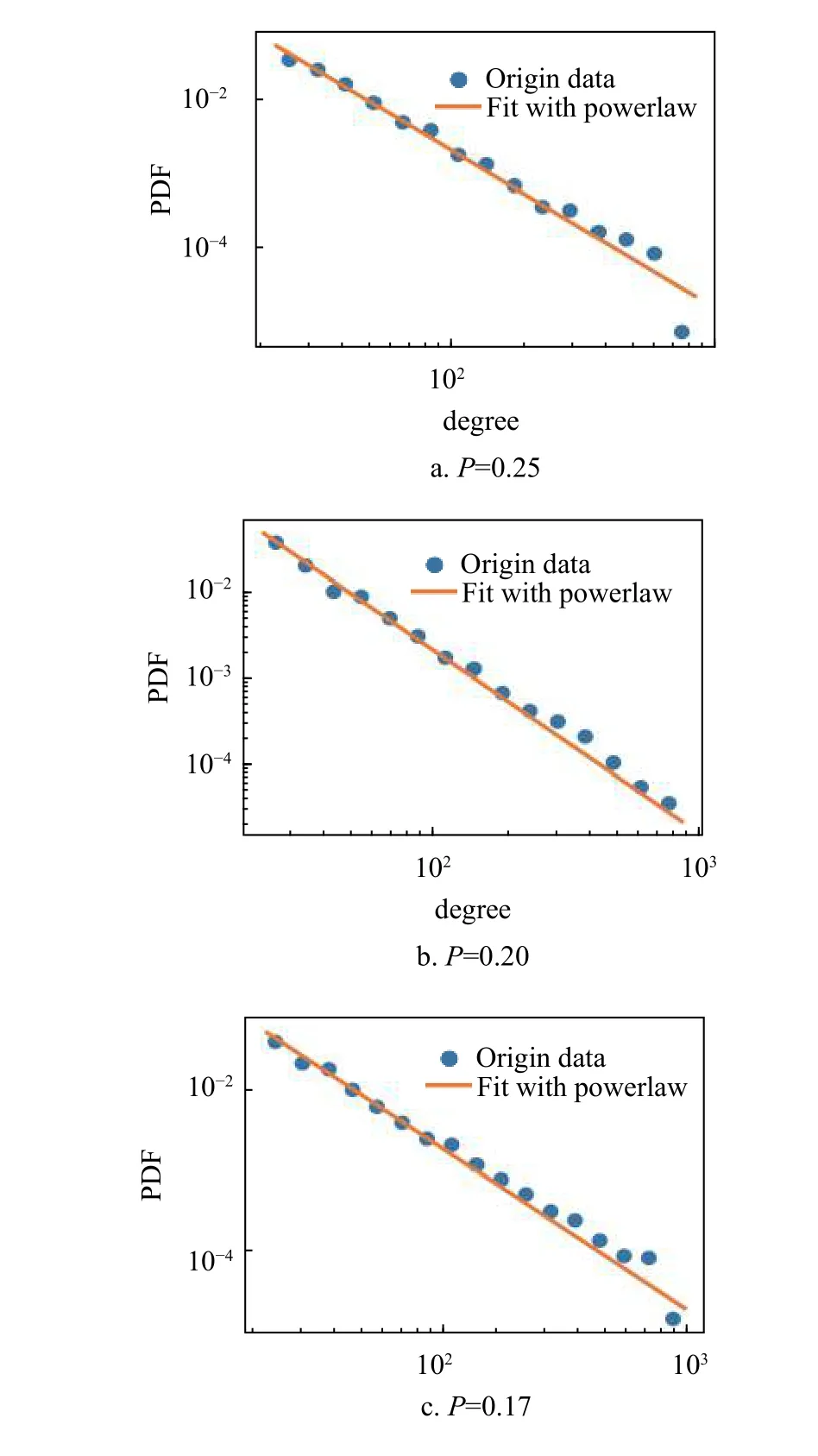
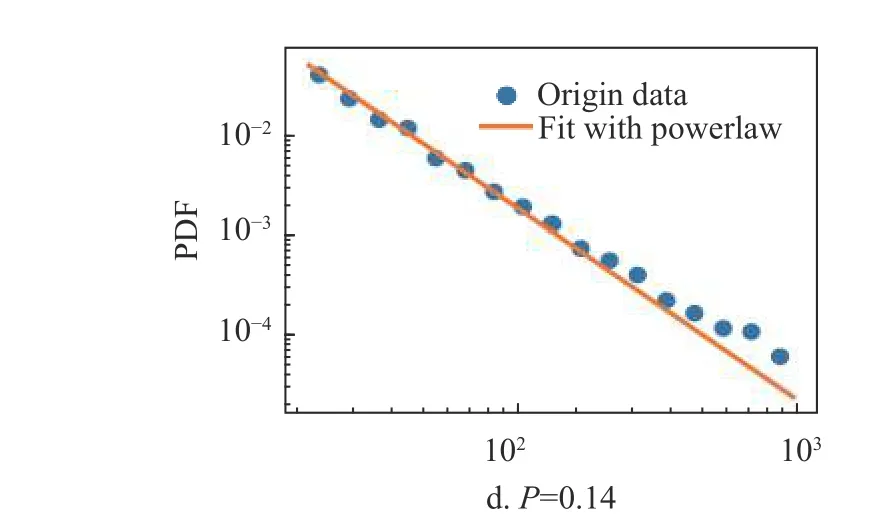
图7 度分布数据和使用幂律分布拟合

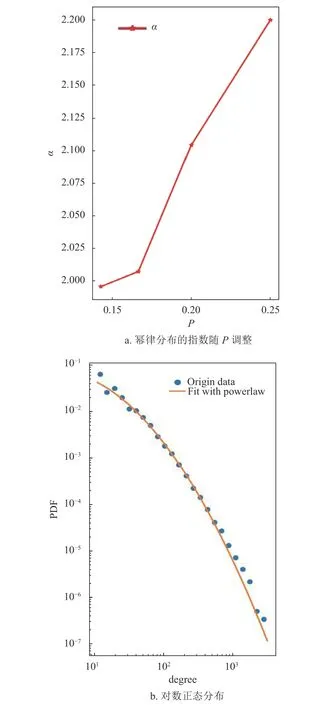
图8 对数正态分布的网络图

2.2 模型验证

为了进一步验证提出的新生成模型适用于知乎标签网络，需要新模型能够根据知乎标签网络的参数，生成仿真的复杂网络。如果仿真的复杂网络的度分布与知乎标签网络的度分布一致，说明本文提出的模型符合知乎标签网络的特点，是有效的。

因此，本文使用从真实数据中提取的 m和 p 值进行仿真，对比真实网络的度分布和仿真网络的度分布，结果如图9，可以发现仿真网络的度分布与真实网络的度分布吻合较好。

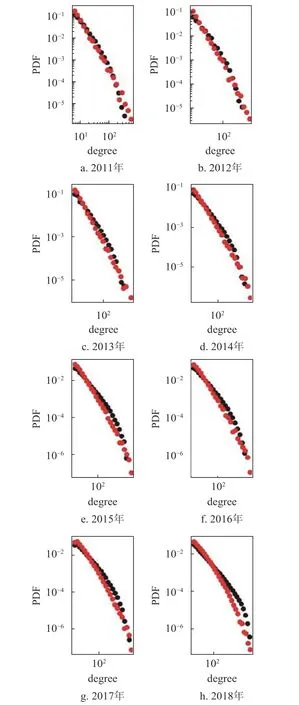
图9 度分布数据图

使用从真实网络中提取的p 值和 m值，对比通过仿真生成的网络的度分布和真实网络的度分布如图9a～图9h，图中的红色数据点代表真实网络的度分布数据，黑色数据点代表仿真网络的度分布数据。知乎标签网络的度分布从幂律分布逐渐向对数正态分布进行演化，在此过程中幂律分布的幂指数也逐步下降。度分布呈现幂律分布代表了网络的度分布呈现一种异化的分布类型，即大多数节点的度都很小，而极少量的节点具有很大的值。幂指数越大，度值较大的节点的占比越小，度分布的异化越明显。知乎标签网络的幂指数的下降以及从幂律分布到对数正态分布的演化都表明，知乎标签网络的度分布在晚期相较早期有一定的均匀化趋势，度分布的异化程度逐渐降低。从知识演化的角度来看，这种变化也在一定程度上反映了社会群体对于知识点的关注从早期的集中化开始逐渐呈现了一定的平均化，也反映了随着时间的发展社会群体的兴趣逐渐呈现一定的多样化趋势。

通过图中真实网络的度分布与仿真网络的度分布的对比，也可以看出根据模型仿真得到的结果十分贴近真实结果，说明了模型中提出的全连接和可变化的新节点比例的假设是有效的。综上所述，该模型从定性和定量的角度都更加接近真实数据，可以解释知乎标签网络的度分布以及演化规律。

3 结 束 语

本文基于2011-2018 年知乎2 034 404 条问答记录的实证数据，深入分析了其标签网络生成特点和统计规律，总结出了知乎标签网络“批量增长”和“交叉连接”特性，并对经典BA 模型假设进行了符合上述特点的修改适配，提出了一种新的标签网络优先连接模型，能够有效地解释知乎标签网络的度分布规律和动态生成机制。

通过仿真模型和实证数据对比发现，知乎标签网络度分布从早期幂律分布逐渐趋于对数正态分布，因此经典BA 模型难以解释此演化过程，且其度分布幂指数也明显小于恒为3 的BA 模型幂指数，但本文提出的标签网络优先连接模型却能很好地描述知乎标签网络的动态生成过程。该模型可以充分利用现有网络节点和新旧节点间相互关系，实现批量交叉连接，能够很好地拟合知乎标签网络的静态结构参数及动态演化机制，这也表明其生成机制确实受到“批量增长”及“交叉连接”这两个特性的控制，且其知识标签的连接确实是不同类型节点间交叉组合连接两两互相连接，而非只有新旧节点间简单随机连接。该模型揭示了标签网络生成机制，还原了标签网络生成过程，实现了调节参数来生成其演化过程中不同幂指数的幂律分布以及对数正态分布，它也适用于其他多种生成过程与标签网络类似的共现网络，如：引文网络和科学家合作网络[22]等。

知乎标签网络作为一种知识网络，它可以代表社会群体对于知识的关注，知乎标签网络的度分布幂指数的减小以及从幂律分布到对数正态分布的演化在一定程度上可以代表人们对于知识的关注点从原本的集中化逐渐变得分散和多样化。同时较小的网络直径和相对较大的集聚系数也代表着不同知识点和学科之间联系比较紧密，在一定程度上体现了现在的学科融合和知识跨界的现象。对于这类知识网络的研究可以帮助我们理解知识网络的形成，为进一步研究社会知识的生成，知识结构的构成、演化与变迁[23]，社会关注点的变化，乃至舆情监控[24]奠定基础。