多传感器系统误差特性匹配的动态估计与补偿算法

邢文革，桂佑林，顾万里

(1. 南京电子技术研究所 南京 210039；2. 东南大学信息科学与工程学院 南京 211189)

作战要素的协同融合是支撑体系作战、提高体系作战效率的重要环节[1-2]。如何将战场上高复杂性和高多样性的信息融合成高质量的作战情报和态势是侦察探测系统面临的难题之一。雷达是现代和未来战争中主要的信息获取手段，雷达组网能扩展信息获取范围、提高侦察系统的精度和可靠性、改善目标航迹和情报的稳定性[3-4]。但在实际应用中，因不同雷达输出数据的误差特性不同，现有融合模型无法充分发挥组网多雷达系统的优势，经常出现不必要的性能退化[5-7]。另外，当参与融合的雷达对象动态变化时，变化的新数据可能使得融合结果稳定性变差，数据分析发现，系统误差不一致或系统误差的变化是重要影响因素。

工程中一般采用检飞和标校等静态方法来减小雷达的系统误差，假定系统误差是稳定、慢变的。但在战场实际使用中，时间的积累、雷达运行环境的变化及敌方对抗等因素，特别是活动的安装平台(如舰船、飞机等)随时会产生或带来误差特性的系统性变化[8]。为了对系统误差进行在线补偿，文献[9-10]研究了系统误差在线估计算法，比较经典的方法有实时质量控制算法[11]、最小二乘算法[12-13]、广义最小二乘算法[14-15]、精确极大似然算法[16-18]、极大似然配准算法[19-20]、卡尔曼滤波算法[21-23]和神经网络算法[24-25]等。上述算法几乎都是利用多部雷达对同一目标多个时刻的原始点迹实现适配，需要预先把不同雷达对同一目标的原始量测在时空维度上关联起来。然而，在存在系统误差的条件下，各传感器原始点迹的系统误差与融合航迹的系统误差不具有一致性，将同一目标来自不同传感器的原始点迹与融合航迹进行预关联容易出现错误[26]，由此可能导致航迹跟踪失败。因此，上述方法对于航迹融合比较有效，在点迹融合层面很难进行工程应用。为了绕过预关联这一困难，文献[27]研究了针对固定目标的系统误差估计方法；文献[28-29]研究了针对合作目标的系统误差估计方法，如已知飞机航线等信息；这类方法已知目标航迹信息，无需进行航迹预关联，对于非合作目标不再适用。目前少有文献研究多传感器系统误差在线估计算法在非合作目标场景下的工程化应用方法。

针对非合作目标场景下，多传感器系统误差估计在工程应用中容易出现预关联错误的问题，本文提出了μ-DECA(μ-dynamic estimation and compensation algorithm)算法，对各传感器之间的系统误差进行动态迭代估计，在预关联之前对各传感器的系统误差进行修正，使得各传感器原始点与融合航迹的系统误差具有一致性，保证多传感器点航迹关联的正确性。本文在大量分析实际工程系统数据特性的基础上，提出直接面向工程应用的多传感器相对误差特性动态估计模型和误差特性适配算法，针对性强、实用性好、适应性广。

1 多传感器融合中误差特性影响分析

一般将传感器测量误差分解为系统误差和随机误差，如：

式中， ei代表第i个传感器对目标测量的总误差；μi代表第i个传感器对目标量测的系统误差； σi代表第i个传感器对目标量测的随机误差，通常随机误差可以建模为零均值的高斯过程； nt代表传感器的个数； μmi代表引起系统误差 μi的 m个因素。如标定残余引起的指向类误差、系统慢漂移等引起的慢变化的偏置类误差、相控阵扫描不一致引起的指向不一致误差、环境变化/多路径等引起的周期性余弦变化的系统性偏置误差、干扰、多目标或机动等引起的动态响应滞后类误差等。

常用的传感器融合算法有加权平均融合算法、卡尔曼滤波、贝叶斯估计、统计决策理论、模糊推理及神经网络等方法。工程上通常采用加权平均融合算法。经对各种实测数据进行的统计发现，这种直接对不同系统误差和随机误差传感器测量值进行融合的方法存在以下问题：

1) 一般假定各传感器误差是随机独立的，但实际系统由于误差的存在，各传感器的数据与融合模型不完全匹配，融合输出质量不稳定；由于没有各传感器系统误差的先验知识，无法对各传感器输入数据的系统误差进行匹配，融合后的系统误差无法达到最优值，因而不能完全获得融合后提高精度、改善目标跟踪稳定性的好处；

2) 当参与融合的传感器种类、数量发生变化时，融合模型无法适应性的变化，融合后的系统误差特性会发生变化，即融合后系统误差特性的一致性和稳定性较差；

3) 如果部分传感器丢点或没有返回测量值，即在k+1时刻只有m 个测量值，有：

即k+1时刻融合后测量误差的系统误差与k时刻融合后测量误差的系统误差不相等，系统误差的一致性、稳定性较差。

因此，在对各传感器测量值融合前必须对传感器进行适配，保证适配后各传感器测量值的系统误差具有一致性。

2 多传感器相对系统误差估计模型及估计算法

2.1 多传感器相对系统误差估计模型

假设雷达组网系统中，各雷达对目标的测量数据为：

式中，(ri,ai,ei)代表第i个雷达对目标的测量值；(r,a,e)代表雷达运动航迹的真值；(μri,μai,μei)代表第i个雷达对目标量测的系统误差；(σri,σai,σei)代表第i个雷达对目标量测的随机误差，通常随机误差可以建模为零均值的高斯过程； n代表雷达组网系统中雷达的个数。

雷达系统误差适配的原理为：在xyz 坐标系下，对(r,a,e)测量值系统误差进行转换以获得系统误差，建立适配补偿模型，在融合前将不同传感器的误差特性转换为相同或相一致的误差特性模型(理想情况下均值为零的高斯分布)，以使融合输入数据与融合模型相匹配。

目标在各雷达坐标系中的真实位置(xi,yi,zi)为：

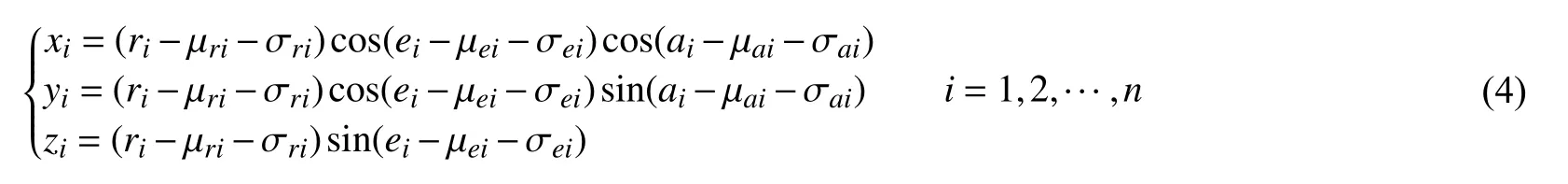
将真实位置在(σri,σai,σei)=[0,0,0]点进行一阶Taylor 展开，则：

即：

式中，

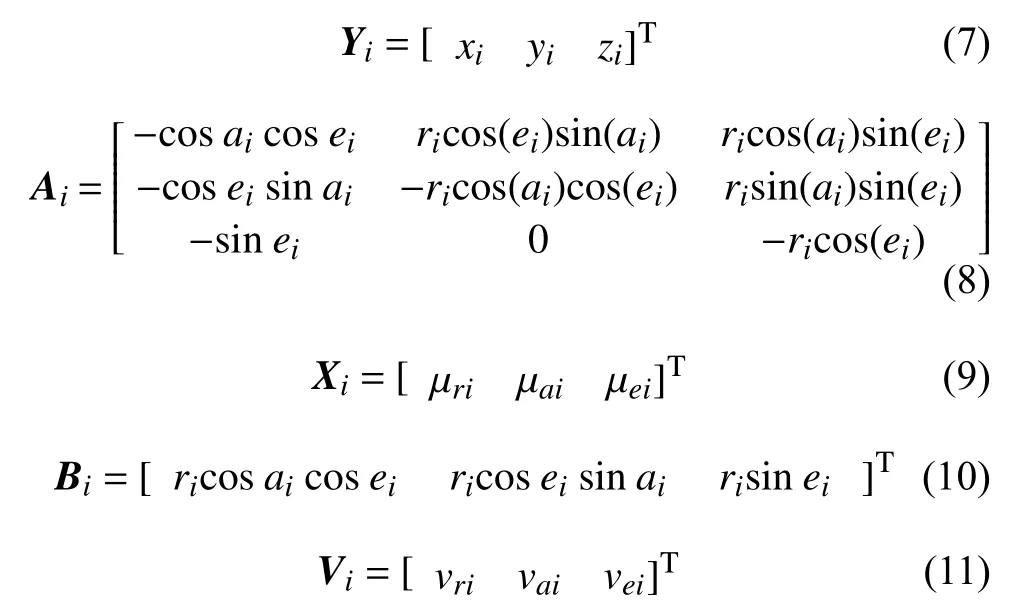
将各雷达数据转换到统一的全局坐标系下，可得：

式中， Ygi代表第i个雷达在全局坐标系下的数据；Ti代表第i个雷达坐标系相对全局坐标系的转换矩阵； Y0i代表第i个雷达局部坐标系原点在全局坐标系下的坐标。

在对多传感器相对系统误差进行估计时，首先需选择系统误差较小的传感器作为基准传感器，且假设基准传感器的系统误差为零，即Xr=0，由此估计其他传感器和基准传感器之间的相对系统误差。

对于同一目标，其在各传感器中的真实位置应该是相等的，即：

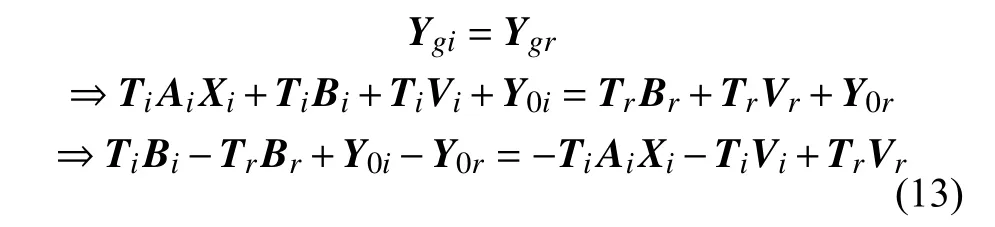
由此整理得：

式中，

对于上述方程，为了减小随机误差对估计精度的影响，需联合多个测量的数据来对系统误差进行估计，即：

式中， m代表测量数据的个数。

2.2 多传感器相对系统误差估计算法

对于上述模型，可以采用实时质量控制算法[11]、最小二乘算法[12]和广义最小二乘算法[15]等方法对各传感器之间的相对系统误差进行估计。在系统误差慢变的情况下，上述算法均能够对其进行精确估计。由于最小二乘算法在工程应用上已经比较成熟，本文采用最小二乘算法来估计传感器系统误差，由此得到：

根据上述方法，可以对各传感器测量数据的相对系统误差进行估计，由此对其进行一致性匹配补偿，再对补偿后的测量数据进行传感器融合处理。

3 μ-DECA 算法框架设计和仿真分析结果

3.1 μ-DECA 算法产品应用框架

对于上文给出的多传感器相对系统误差估计算法，在工程应用过程中需要预先把不同雷达对同一目标的原始量测在时空维度上关联起来，对同一目标关联成功的点迹，进行相对误差估计，然后再对点迹进行相对误差补偿。但是，在存在系统误差的条件下，各传感器原始点迹的系统误差与融合航迹的系统误差不具有一致性，将同一目标来自不同传感器的原始点迹与融合航迹进行预关联容易出现错误，引起相对误差估计和补偿错误。因此，针对上述工程应用困难，本文设计了如图1 所示的多传感器相对系统误差动态适配性处理算法，该方法能够克服预关联的困难，满足工程化需求。

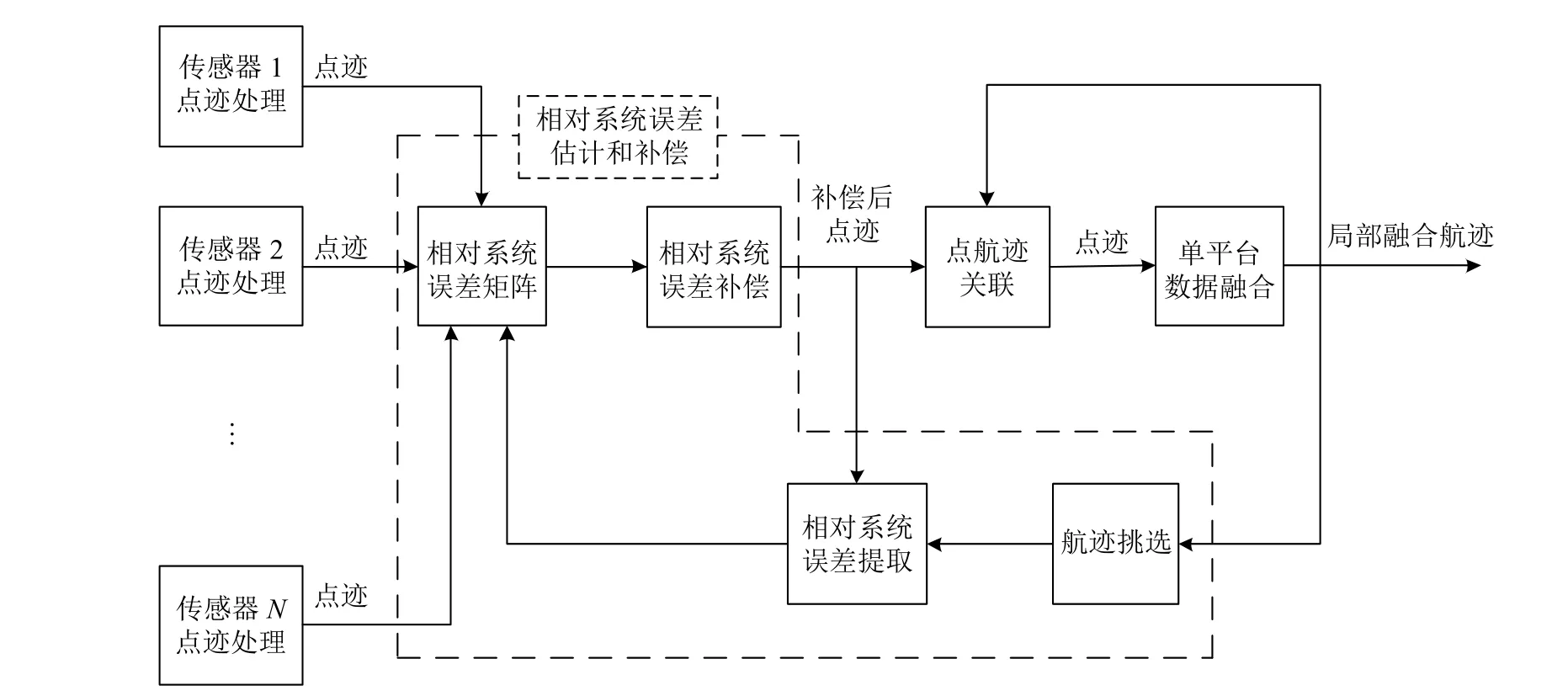
图1 短基线多传感器融合示意图

3.2 μ-DECA 算法实测数据验证

为了验证本文算法的普适性，分别采用某型同平面安装航管一二次雷达、某一船载平台上非同一平面两部雷达和两部短基线部署的双波段雷达等不同场景实测数据进行验证。

场景一：船载平台实测数据

对于两部0.1 s 数据率的雷达，其距离、方位、仰角测量误差如图2 所示。图中蓝色曲线为相对系统误差估计值，红色曲线为相对系统误差真值。

图2 舰用平台测量误差

根据图2 的误差曲线可以看出，两部雷达测量误差的均值不重合，即两部雷达的相对系统误差不为零，采用本文算法对其相对系统误差进行估计，估计结果如图3 所示。图中蓝色曲线为相对系统误差估计值，红色曲线为相对系统误差真值。

图3 舰用平台相对系统误差估计

根据图3 的相对系统误差估计结果可以看出，本文提出的估计算法具有较快的收敛性，相对系统误差估计值能够在3 s 内收敛到真实值附近。另外，估计的相对系统误差值具有较高的精度，估计误差最大值仅为6%。由此验证了估计算法的有效性。

基于图3 中的相对误差估计值，对两部雷达的测量值进行融合，将融合结果与文献[30]中融合算法的融合结果进行对比，对比曲线如图4 所示。图中蓝色曲线为文献[30]中研究方法，红色曲线为本文研究方法。

图4 舰用平台融合点迹误差对比

从上述实测数据验证效果可明显看出，本文提出的μ-DECA 模型和算法能够较好地补偿雷达1 和雷达2 的相对系统误差，融合点迹的系统误差与两部雷达系统误差的最小值相当，由此提高了融合点迹的精度。同文献[30]中的融合算法相比较，本文方法较好地补偿了相对系统误差，具有较高的精度。在此基础上，本文以距离维测量误差为例，采用概率密度统计的方法来比较本文方法的优势，如图5 所示。可以看出，雷达1 和雷达2 测量误差特性不一致。图5 中绿色曲线代表采用本文算法以雷达2 为基准对雷达1 系统误差进行补偿后点迹误差的概率分布图，其系统误差与雷达2 的系统误差相当。对补偿后的点迹进行融合，融合点迹误差的概率分布图如图中红线所示，其均值与雷达1 和雷达2 测量误差的最小值相等，具有较高的精度。采用文献[30]研究方法对上述点迹进行融合，系统误差较大，由此体现了本文算法的优势。

图5 距离维度点迹误差概率分布图

场景二：航管一二次雷达实测数据

基于数据率为1 s 的航管数据，对距离和方位测量值相对系统误差估计如图6 所示。图中蓝色曲线为相对系统误差估计值，红色曲线为相对系统误差真值。

图6 航管距离和方位的相对系统误差估计值

由此可以看出，μ-DECA 算法具有较快的收敛性，且能够较好地估计一次和二次波段的相对系统误差。

场景三：短基线的两部雷达实测数据

基于数据率为0.2 s 双波段雷达数据，距离、方位和仰角测量值相对系统误差估计如图7 所示，图中蓝色曲线为相对系统误差估计值，红色曲线为相对系统误差真值。

对于上述实测数据验证效果，图7 代表雷达1 和雷达2 在距离、方位和仰角维度上的相对测量误差值以及估计的相对系统误差。由此可以看出，μ-DECA 算法具有较快的收敛性，且能够较好地估计两部雷达的相对系统误差。

图7 短基线双波段雷达距离的相对误差估计值

4 结 束 语

本文提出了一种面向工程应用的多传感器相对系统误差实时估计模型和误差特性动态适配性处理算法(μ-DECA 算法)，可以较好地解决多传感器网络中各传感器误差特性不一致带来的融合结果不稳定的问题。通过不同设备多个场景的实测数据验证了该算法能够提高多传感器融合的精度和稳定性，具有很强的工程应用性。该算法有望应用到跨平台分布式协同探测场合，具有很好的扩展前景。