狄克逊检验法滤波RSSI 的室内定位算法*

王建强代 阳雷倩芳

(东华理工大学测绘工程学院，江西 南昌330013)

随着无线网络通信技术的发展，无线传感网络(Wireless Sensor Network，WSN)节点定位成为现阶段室内位置服务的研究热点。 目前解决WSN 节点定位的主要技术方法是基于测距定位和非测距定位[1]，测距算法包括接收信号强度指示(Received Signal Strength Indication，RSSI)、到达时间差(Time Difference of Arrival，TDOA)、到达时间(Time of Arrival，TOA)和到达角(Angle of Arrival，AOA)[2]，非测距算法包括质心算法[3]。 综合考虑系统部署难易程度、硬件成本以及精度等因素，基于Wi- Fi、蓝牙RSSI 室内定位技术仍然是主流研究热点。

基于RSSI 的室内定位技术是WSN 节点定位中最经典的方法之一，该方法包括RSSI 测距模型和定位算法两部分，大量学者对其进行了深入研究。 针对RSSI 测距模型，任克强等[4]利用高斯滤波对RSSI 观测数据进行优化，根据接入点(Access Point，AP)间距离和RSSI 值动态修正RSSI 模型参数，从而提高测距精度，但该方法忽略了偏离高斯分布的RSSI 异常值对滤波结果的影响；李桢等[5]利用基于M 估计的抗差kalman 滤波方法估计信号强度，得到相对稳定的无线信号，但是抗差滤波需要大量样本数据且算法较为复杂。 针对RSSI 定位算法部分，Xue 等[6]对不均匀空间分辨率下的RSSI 进行物理距离加权定位，通过对短时间内的RSSI 观测值做均值处理，利用RSSI 物理距离差分定权，最终平均定位精度维持在3 m～6 m 之间；唐宗山等[7]提出了一种基于最大似然估计的RSSI 定位算法，通过信号差分改进最小二乘定位算法，实现了15 m 范围内平均定位精度2 m 左右。 上述改进方法在一定程度上可以提高RSSI 定位精度，但利用物理距离加权易受测距模型参数误差影响，无线信号也并不严格服从高斯分布，对定位精度的提升效果并不明显。 因而有必要探索更为接近无线信号传播规律的滤波模型。

针对RSSI 异常值以及测距模型参数误差等问题，本文采用狄克逊检验法[8]滤波RSSI 进行高斯牛顿[9]定位(Dixon text Filter RSSI Gauss-Newton，DFRSSI-GN)。 根据RSSI 偏态分布[10]来衡量其偏斜程度从而利用狄克逊检验法剔除RSSI 异常值，得到近似服从高斯分布的信号，该滤波算法可以同时检测一维观测信号两端的异常值，且易于抗差Kalman 滤波算法；再对修正后的RSSI 进行高斯均值滤波，采用非线性回归模型[11]确定信号衰减模型参数，通过滤波后的RSSI 确定目标点各个方向的权值进行高斯牛顿迭代定位。

1 RSSI 测距模型

基于RSSI 的测距原理是根据无线信号衰减模型[12]将发射端与接收端之间的信号强度利用对数模型转化为距离，可表示为

Pr表示在室内空间中到信号发射端任意距离d处接收端获取的信号强度，一般用RSSI 表示；Pr0表示距离信号发射端d0＝1 m 处的信号强度，用A代替；n表示环境衰减因子；ξ表示服从(0，μ2)分布的环境遮蔽因子，在实际计算中常用0 代替。 所以信号发射端与接收端的距离可由式(1)简化为

2 RSSI 滤波处理及参数估计

就RSSI 定位而言，节点定位的精度取决于信号强度观测样本质量的好坏。 对于复杂环境的室内环境下，利用RSSI 进行定位需要对观测样本数据进行滤波处理以及测距模型参数的确定。

2.1 偏度分析

偏度是统计观测样本数据偏斜方向和程度的度量，通过判断偏度大小确定信号的分布[13]情况。 对于一组RSSI 观测样本数据可表示为:

则RSS 的偏度可表示为

式中:μ，σ分别表示RSSI 值的期望和方差

当Skew(RSSI)＝0 时，样本数据为正态分布；Skew(RSSI)＜0 时，样本数据左偏；Skew(RSSI)＞0时，样本数据右偏。

2.2 狄克逊检验法混合滤波

狄克逊检验法是采用极差比的方法检验观测数据中最大值最小值是否为异常值。 具体步骤如下:

①将RSSI 观测样本按照从小到大顺序依次排列得到rssi1＜rssi2＜…＜rssin，假设检验显著水平α＝0.05，则临界值为D(α，n)；

②检验高端异常值γ11和低端异常值:

式中:rssie是距最大值rssin最近且不等的样本数据值；rssif是距最小值rssi1最近且不等的样本数据值。

④剔除RSSI 观测样本中的异常值后重复步骤①～步骤③，直到未检测到异常值。

图1 狄克逊检验法处理前后偏度对比

通过狄克逊检验法剔除RSSI 异常值能有效降低样本数据偏度，记为RSSI-D。 对建立测距模型的RSSI 数据做偏度态统计分析，从图1 看出狄克逊检验法滤波后的偏度明显降低，此时RSSI-D更加近似服从正态分布，可再次进行高斯均值滤波处理。

RSSI-D近似服从(μ，σ2)正太分布，密度函数为

式中:

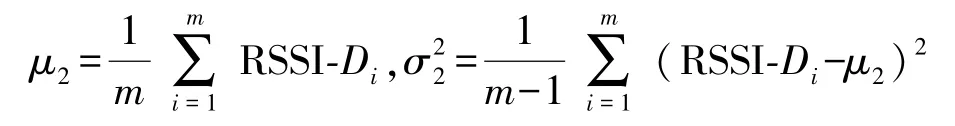
将落在(μ2-3σ2，μ2＋3σ2)的RSSI-Di作为高斯滤波输出值[14]，记为RSSI-DG，利用均值滤波对高斯滤波输出值进行均值处理，最后得到高斯-均值滤波输出值RSSIfilter。

2.3 参数估计

RSSI 测距算法精度取决于参数A，n的选择。传统测量方法中一般将n用经验值进行代替。 为了保证测距的精度，通过对室内某个蓝牙标签不同距离下的信号进行连续观测建立测距模型；对不同距离下得到的RSSI 序列采用本文方法进行处理；再利用非线性回归模型对参数进行多次拟合估计，进而得到符合环境的衰减模型参数A，n。 当剩余观测值与第i次拟合曲线间的平均误差小于0.5 dBm 时，即可将第i次拟合参数作为输出值输出。

3 Gauss-Newton 定位模型

在室内布设M(M＞4)个蓝牙标签和N个目标点，并建立独立室内坐标系，通过测量技术获取蓝牙标签和目标点位置信息。 将蓝牙标签的坐标记为APm＝(am，bm)，(m＝1，2…M)，假设第n个目标点坐标为RPn＝(xn，yn)，(n＝1，2…N)，该点对第m个蓝牙标签观测信号强度为RSSImn＝(rssimn1，rssimn2，…，rssimnk)，通过滤波处理后代入式(2)得到目标点和蓝牙标签间距离为dm，则该目标点的观测方程为

一般用X＝(x，y)T表示目标点坐标的真值，但在实际实验过程中真值无法获取，所以常用估值代替真值；L＝(d1，d2…dM)T表示目标点和蓝牙标签间距离是观测方程的非线性函数的向量表示；V＝(vx，vy)T为目标点坐标的改正数向量，得到非线性误差方程

当M＝3 时，可根据三边定位[15]算法计算目标点的初始位置Xo＝(S-1t)/2，其中

Gauss-Newton 迭代法基本出发点是对非线性误差方程(8)在目标点初始位置X0处线性化，并按照最小二乘[16]估计一次近似值X1，再以X1为近似值进行反复迭代，直到前后两次VTPV值相等。 对于非线性误差方程(8)在X0处存在一阶连续偏导，且目标点的坐标分量之间相互独立，在该点按照Taylor 展开[17]取至一次项，得误差方程

式中:B是f(X)对X的雅克比矩阵，dX表示估值和初始值的误差向量，即

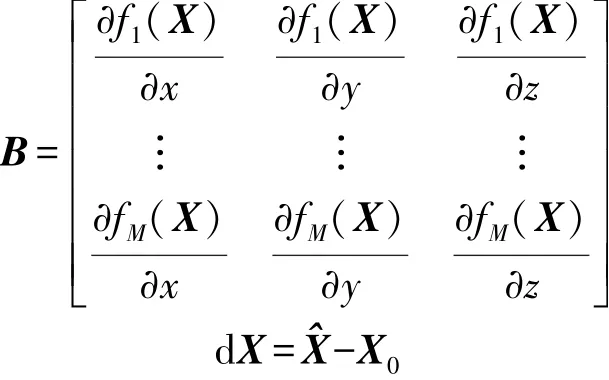
考虑到目标点到蓝牙标签的距离取决于RSSI观测量，若选用距离作为权因子，会受到信号衰减模型中参数误差的影响，所以本文选择用滤波后的信号强度对目标点到蓝牙标签的距离进行加权，权因子记为ωk，权矩阵记为P

在X＝X0处根据最小二乘原理可得

根据X1为近似值继续迭代，其迭代公式为

当(VTPV)K＝(VTPV)K＋1时，停止迭代。

目标点估计位置与真实位置间的距离可作为精度衡量指标，即

4 实验与分析

实验数据来源于“UPINLBS2019 室内定位比赛”的实测数据。 在一条长65 m，宽3 m，高3.94 m的走廊搭建蓝牙室内定位环境，选取场景内的14 个蓝牙标签和6 个目标点，实测数据包括独立坐标系下蓝牙标签和目标点的相对坐标，各个目标点连续观测的信号强度数据以及建立测距模型所需要的数据。 同时选择了一条长15 m 的直线，对相同蓝牙标签每隔0.3 m 采集一组信号强度，共50 组数据用于拟合信号衰减模型参数。 通过剔除偏差较大的观测数据并进行多次拟合，结果如图2 所示，得到环境拟合参数A＝-57.054，n＝2.220。

图2 衰减模型曲线拟合

表1 是衡量图2 中拟合精确度的指标，其中和方差(SSE)和中误差(RMSE)值越小则拟合程度越高，确定系数(R-square)和校正确定系数(Adjust R-square)值越接近1 则曲线拟合越好。 通过狄克逊检验法不断剔除误差较大的RSSI 观测数据，经过6次拟合，首次得到观测数据和拟合曲线间的平均误差为0.355 dBm，所以将第6 次拟合参数作为符合环境的衰减模型参数输出。

表1 拟合参数精度指标

在实验中对实测样本数据分别实现了RSSI 测距定位、最小二乘法定位以及DF-RSSI-GN 算法定位。 前两种定位算法中信号衰减参数均采用经验估值，DF-RSSI-GN 算法中的信号衰减参数采用本文拟合的结果。 表2 为三种算法的定位结果和已知坐标的差值。

表2 三种定位算法对比 单位:m

通过对连续观测的蓝牙信号强度值进行狄克逊检验法滤波处理，可以有效的剔除异常值。 在得到稳定的信号强度值的基础上，进行Gauss-Newton 定位。 实验结果如表2 所示，从表中可以看出:DF-RSSI-GN 定位算法平均点位误差为1.6 m，定位精度明显优于RSSI 方法的7.9 m 和最小二乘定位算法的4.8 m；利用文献[14]中混合滤波算法优化RSSI 和文献[18]中牛顿迭代定位算法对本文数据进行处理得到平均点位误差为3.2 m，对比显示本文DF-RSSI-GN 算法的定位精度也具有明显优势。

实验对目标点实现了RSSI 测距定位、最小二乘法定位以及利用DF-RSSI-GN 算法进行定位，估计点位结果和真实点位对比如图3 所示，通过DFRSSI-GN 算法估计的点位误差明显小于现有的定位算法。

图3 三种定位算法和真实点位

图4 为三种定位算法以及狄克逊检验前Gauss-Newton 算法的定位误差示意图。 从图中可以看出DF-RSSI-GN 算法定位误差基本稳定在0 ～3 m 范围内，精度明显高于RSSI 测距定位和最小二乘定位。为了验证狄克逊检验法剔除异常值对定位结果的影响，实验还对比了狄克逊检验前后的Gauss-Newton定位算法。 其中狄克逊检验法滤波后的Gauss-Newton 定位算法指本文的DF-RSSI-GN 算法，狄克逊检验法滤波前的Gauss-Newton 定位算法并未进行狄克逊检验法滤波剔除RSSI 异常值，对RSSI 样本数据直接采用高斯滤波，通过非线性回归拟合信号衰减模型参数，最后通过Gauss-Newton 迭代定位。 对比结果如图4 显示目标点4 和目标点5 的精度明显高于狄克逊检验法处理前的精度，通过狄克逊检验法剔除RSSI 异常值对提高点位精度有一定效果。

图4 点位误差

5 结语

本文针对无线传感网络节点定位中的无线信号异常值以及测距模型参数误差进行了研究，根据RSSI 偏态特性对其进行了狄克逊检验法滤波和高斯均值滤波处理，采用非线性回归模型估计衰减模型参数，最后采用Gauss-Newton 迭代得到最优位置。 实验结果表明本文DF-RSSI-GN 算法中利用狄克逊检验滤波剔除RSSI 异常值可以避免小概率大干扰的离群值对滤波结果造成影响，同时还可以提高RSSI 测距精度；通过滤波后的RSSI 值代替物理距离确定权因子可以减少测距模型参数误差造成的权误差；利用高斯牛顿定位迭代算法可以不断修正点位偏差；相较于现有的改进定位算法，本文算法的定位精度有明显提升。 但是本文只考虑了静止目标点定位，动态定位有待下一步研究。