基于曲面拟合的NDIR 单通道CO2 气体传感器快速标定算法*
2021-04-08陈凯彦朱斌成毛科技
陈凯彦朱斌成毛科技*
(1.浙江工业大学土木工程学院,浙江 杭州310023;2.浙江工业大学计算机科学与技术学院,浙江 杭州310023)
二氧化碳(CO2)是环境大气以及燃烧废气的主要成分,同时也是重要的化工原料,在农业、工业、环境监测、卫生防疫及宇航生保等领域都需要对CO2气体浓度进行高灵敏度检测[1]。 二氧化碳浓度检测主要使用CO2气体传感器。 随着环境保护、卫生防疫、国防科研、能源化工、医疗诊断等领域科技的高速发展,传统的CO2气体传感器检测方法已经无法满足前沿领域对CO2浓度检测的需求[2]。 如何在降低检测成本的同时,提高CO2气体传感器的测量精确度,无疑具有相当重要的研究意义和应用价值。
检测CO2气体的传感器有气相色谱分析仪传感器、固态电解质传感器、电化学式传感器、催化燃烧式传感器、半导体传感器等[3],相较于这些气体传感器,红外吸收光谱式传感器优点较为明显,具有测量范围大、选择性好、响应灵敏度高、抗干扰能力强、准确性高等特点[4]。 红外吸收光谱式传感器需要先分离出特定波长的红外光,分光方法可分为滤光片法和棱镜法。 其中棱镜法由于需要机械转动,并不适用于便携式或现场式仪器,因此这些场合滤光片法是首选。 滤光片法不能将红外光波长分为单波长,因此也称为非色散红外检测法,即NDIR(Non-Dispersion Infrared)[5]。 基 于NDIR 技 术 的CO2气体传感器具有设计简单,便携性好,维护成本低,使用寿命长等优点,在CO2的气体浓度检测中得到了广泛应用。 根据红外探测器通道数,非色散红外CO2气体传感器可分为单通道和双通道两种,单通道传感器设计简单,成本低,应用场景比较广。本文主要针对NDIR 单通道CO2气体传感器提出一种准确性和可靠性高的快速标定算法。
CO2气体传感器在使用之前需要进行传感器的标定。 传感器的标定是指通过传感器的测量试验,建立传感器输出电压与气体浓度之间的关系式。 然而,除了CO2气体浓度本身,温度,压强,以及传感器的制作材料、工艺等都会对传感器的输出电压有影响,导致传感器测量的浓度值与真实值存在一定的偏差[6]。 对传感器进行标定,以保证测量的准确性,对于CO2气体浓度的准确检测来说十分重要。但是,传感器标定的高准确性往往需要较复杂的算法和较高的时间成本和人力物力成本。 因此,如何既高效又准确地对气体传感器进行标定具有非常现实的意义。 文献[7]利用红外吸收原理研制了测量CO2浓度的测试仪,对固定浓度的CO2气体(标气瓶)进行检测,并对测得的数据进行函数关系拟合,由此得到CO2浓度与探测信号之间的关系式。 但由于过少的数据难以保证拟合曲线的连续性,而为得到大量数据不仅费时,且需要采购大量标准浓度的气体,花费的成本较大。 文献[8]采用参考标定法,利用一个现有的气体传感器来对设计的气体传感器进行标定,但由于所参考的气体传感器本身存在误差,影响了标定的精度。 文献[9]针对NDIR 分析仪测量CO2浓度,考虑到气体间交叉干扰,压强和温度对测量结果的影响,介绍了一种修正这些影响的方法,该方法虽然减小了测量误差,但该方法标定效率较低。 文献[10]针对温度变化对红外CO2气体传感器测量的影响,提出了一种基于L-M 贝叶斯正则化BP 神经网络进行温度补偿的方法,该方法算法复杂,过程繁锁。
总体来说,国内红外CO2气体传感器技术虽然有了一定的发展,但由于研究起步较晚,与国外红外CO2气体传感器领域还有较大的差距[11-12]。 目前的传感器标定算法普遍存在着标定算法复杂,标定效率低,精度不高等问题[13]。 采用高效准确的标定算法是确保红外CO2传感器测量成效的关键一步,为此针对NDIR 单通道CO2气体传感器提出了一种基于曲面拟合的快速标定算法。 实验表明,该算法在保证精度的情况下,具有标定速度快,简单便捷,高效低成本的特点。
1 红外气体传感原理
红外气体传感原理是基于不同气体分子的红外光谱选择吸收特性,利用气体浓度与吸收强度关系来确定气体的浓度。 红外吸收式传感器结构如图1所示,主要包括红外光源,吸收池,滤光片等。

图1 红外吸收式传感器结构示意图
红外光子的能量与辐射频率具有对应关系,如式(1):

式中:E为红外光子能量,h为普朗克常量,v为频率。
分子结构内部的运动状态决定着分子的能量[14]。 气体分子在接受红外光照射时,吸收红外光辐射能量,引发分子结构内部的振动和转动,从而改变分子运动状态。 分子的能级相应地发生变化,产生分子光谱。 当红外光子的能量与气体能级差相一致时,引发强烈的吸收,如式(2)所示:

式中:E1和E2为跃迁前后的能级能量。
不同的分子吸收不同波长的红外光进行能级的跃迁,不同能级之间的跃迁吸收的能量不同。 某种气体只能吸收一定波长的光。 朗伯-比尔定律是光吸收的基本定律,是气体传感技术的理论依据[15]。红外光照射于吸收介质,在通过一定厚度的介质后,介质吸收了一部分光能,红外光的强度减弱。 吸收介质的浓度越大,介质的厚度越大,光强度的减弱就越显著。 朗伯-比尔定律示意图如图2 所示。
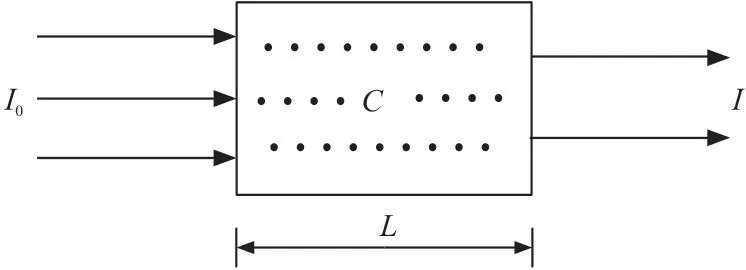
图2 朗伯-比尔定律示意图
其公式表述如下:

式中:I0为红外辐射的初始能量;I为红外辐射通过被测气体后的光强;C为被测气体的浓度;L为红外辐射通过气体层的厚度;K为吸收系数,该系数取决于被测气体的吸收谱线。
从理论上来说,通过测量获取红外辐射的初始能量I0和红外辐射被气体吸收后的能量I,就能检测出气体浓度C。 实际应用中,由于光源的发射强度的峰值所处的波段会变化,I0较难精确测定,气体吸收系数K也与滤光片的中心波长相关;同时,传感器的性能也会受到气体压强和环境温度的影响。 因此,将朗伯-比尔定律直接应用到实际的测试中并不现实,需要采取一定的方法来消除这些不可控因素。
在实际操作中,利用数据反演理论,对朗伯—比尔定律进行修正。 测试数据采集中,采集到的信号是与光强信号呈一定比例关系的电压信号。 利用采集的电压值,计算出电压信号与光强信号的比值,由此获取吸光度。 根据数据反演理论,对多组标准气体进行传感器标定,拟合出反映CO2气体浓度和吸光度关系的多项式函数。 然后,利用所获取的气体吸光度,再根据函数反演理论,推算出被测CO2气体的浓度值。
2 快速标定算法的设计
在实际应用中,基于NDIR 的CO2传感器测量的精度受到温度、压力、气体交叉干扰等影响[16],其中,受温度因素干扰的影响程度最大。 因此,针对不同温度条件进行CO2传感器标定十分重要。
标定算法的总体思路如下:对传感器施加一定浓度的气体,通过A/D 转换使每个测量值以不同的电压值输出;对传感器输出的电压值数据处理后,将测量气体的标定浓度与其对应的温度及输出电压进行曲面拟合,得到拟合系数,从而确定CO2气体传感器输出与输入的关系。
主要步骤如下:
步骤1 取N个没有经过校准的传感器节点,对其中每个节点,采集m个不同环境温度、不同CO2浓度下的传感节点输出电压值,N的取值越大可得到越多的候选拟合曲面,m取值越大可得到越精确的拟合曲面。 同时,这两个参数越大,也会消耗越多的采集时间与成本。
步骤2 对上述获得每个传感器的m个传感节点电压值进行归一化处理,归一化的公式为式(4),经过归一化处理后的数据范围属于[0,1];

式中:X*为经过归一化处理后的数据,X为传感节点的某个环境温度、某个CO2浓度下的输出电压,Xmax为m个传感节点的所有输出电压中的最大值,Xmin为m个传感节点的所有输出电压中的最小值,归一化处理是为了数据被限定在一定范围内,消除奇异样本数据的影响。
步骤3 对每个传感器节点,使用其m个数据点,进行曲面拟合,曲面拟合函数为式(5)。

式中:U表示节点输出电压值的归一化值,T表示环境温度,C表示二氧化碳浓度。
步骤4 对一个新生产的待标定的传感器节点,针对3 个温度,测量每个温度下2 个CO2浓度点所对应的节点输出电压,共得到6 个数据点。
步骤5 对N个上述的拟合曲面(即拟合函数中的每一个),分别进行如下操作:将每个数据点的温度和输出电压的归一化值作为模型的输入值,得到模型输出值,计算该输出值与该数据点CO2浓度的差值,最终根据这6 个差值计算得到它们的绝对值之和。
步骤6 在N个上述的拟合曲面中,挑选出绝对值之和最小的那个拟合曲面,作为该节点的CO2浓度估计模型。
3 标定试验与标定结果分析
3.1 标定试验与结果
浓度标定的目的是获得不同温度T,不同浓度C下的模组输出的电压AD 值U,即获得(T,C,U)组。 为了得到不同温度条件下的实验数据,需要使用能够对温度进行定量调节和控制的实验设备。 本实验采用气体温度标定箱进行温度标定,利用CO2气体标气瓶,瓶中的混合气为氮气,采用性能良好的CO2气体传感器样品进行测试实验。 实验采用了400×10-6,450 ×10-6,500 ×10-6,1 000 ×10-6,1 500×10-6,2 000×10-6浓度的标准CO2气体,在气体温度标定箱内做测试实验,温度控制在0 ℃~48 ℃范围内,每隔一定温度作为测试点,采集测试节点在不同温度和不同浓度下传感器模组输出AD 值的变化,利用采集的数据采用曲面拟合的方法来进行浓度值预测。 标定步骤如下:
①设定温度。 首先将传感器样机放入气体温度标定箱内,将气体温度标定箱温度设定为一个温度值后,等待温度环境恒定1 h。
②添加气体。 打开CO2标气瓶,通入气体,等待3 min,直至气室内充满标准浓度的气体。
③记录下装置测量通道的AD 值,腔内温度值T。
④重复以上步骤,改变温度箱设置,在0 ℃~48℃范围内每隔一定温度作为测试点,并记录实验结果。
随着城镇化战略的推进和城区面积的不断扩张,干线公路所在的城市外围区域逐渐被纳入城市的规划建设范围内,成为城市区域范围内的主要通道。人口的大量集聚以及公路的街道化,使得逐渐被包围进入城市腹地的干线公路,使用属性逐渐转变为城市道路,但干线公路难以直接作为城市道路使用,并且其功能不能同时满足对外交通和城市内部交通的需求。因此,很多城市陆续开始对干线公路进行快速化改造。
⑤改变气体浓度,重复1 至4 步的过程,测试并记录实验结果。
⑥整理试验数据,计算拟合系数矩阵,分析性能指标,确定标定算法的精度。
实验共采集了67 个待标定的传感器节点在不同温度,不同浓度下对应的AD 值,每个待标定的传感器分别测得184 个AD 值。 将采集到的不同温度,不同浓度下的AD 值整理成Excel 数据表格,如表1 所示(表1 中只列了浓度400×10-6时部分数据)。 由于输出电压只与腔内温度有关,表中温度采用的是传感器的腔内温度。 每个传感器对应一张Excel 数据表。
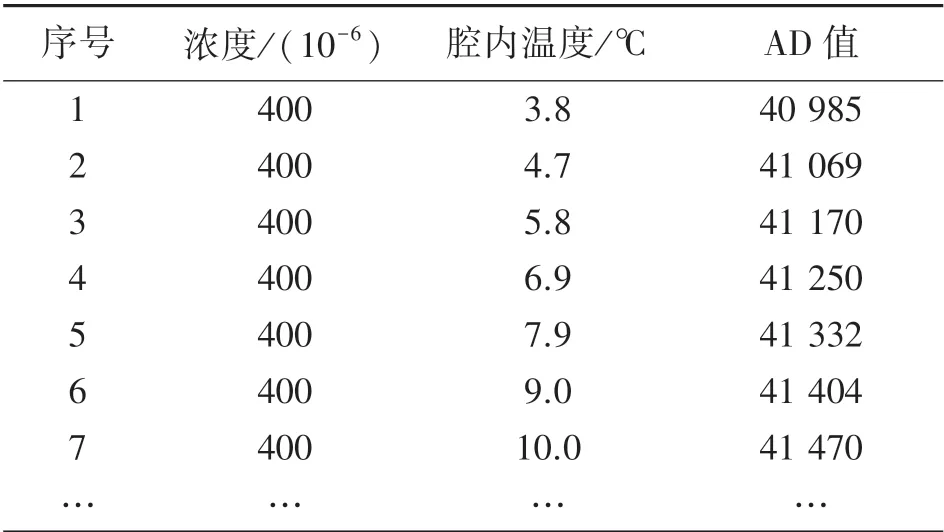
表1 拟合数据
实验使用MATLAB 进行加权最小二乘法曲面拟合,所使用参数如下表2 所示,采用双5 次系数(poly55)拟合曲面:

表2 拟合参数
由于标准曲面所涉及的浓度范围一般较宽,而样品测试的绝对误差往往又随浓度的增大而增大,如果以普通最小二乘法加以拟合,则会导致标准曲面在高浓度区域内精确度较高,而在低浓度区域内准确性明显下降。 标准曲面侧重的是相对误差而不是绝对误差,不同浓度区域内的相对误差和绝对误差通常情况下不成比例,比如浓度在100×10-6时,1×10-6的误差仅使其相对误差达到1%,而当浓度为1×10-6,相对误差则达到了100%。 因此,为了保证曲面精度,需要在拟合时对低浓度数据给予较高的权重。
图3 拟合后的曲面示意图
67 行拟合系数对应67 个曲面,将这些拟合曲面作为候选曲面。 实验中,对一个新生产的待标定的传感器节点,针对3 个箱内温度(试验中采用了5 ℃,20 ℃,35 ℃),测量每个温度下2 个二氧化碳浓度点(试验采用了400×10-6和2 000×10-6)所对应的节点输出AD 值,共得到6 个数据点;根据这6个数据点的值,从67 个候选曲面中选取一个曲面作为该传感器的特征曲面。 选取方法为:读取侯选曲面的系数,获取曲面方程,进行循环计算,求得各个传感器节点的浓度预测值,从中挑选最小均方误差所对应的曲面方程作为该传感器的特征曲面。
实验选取了240 个传感器节点作为测试,在得到上述67 个候选曲面后,通过前述方法对240 个传感器进行标定,为每个传感器选定一个特征曲面。在完成了240 个传感器的标定后,实验随后选取了15 ℃,25 ℃两个温度下不同浓度(分别为400×10-6、 1 000×10-6、 1 500×10-6、 2 000×10-6、 4 000×10-6)的10 个测试点,得到每个传感器的测试值和真实浓度的对比值,如表3 所示。 根据拟合系数获得的CO2气体浓度与实际浓度之间存在一定程度上的偏差,其偏差大小代表了传感器测量精度的高低。 以表3 中第一行数据为例,测试浓度为410×10-6,真实浓度为400×10-6,偏差为10×10-6,偏差率为2.5%。 综合各行数据,若以偏差率是否在5%+50×10-6的精度内来衡量标定是否合格,实验统计结果表明,算法标定的合格率为99%。
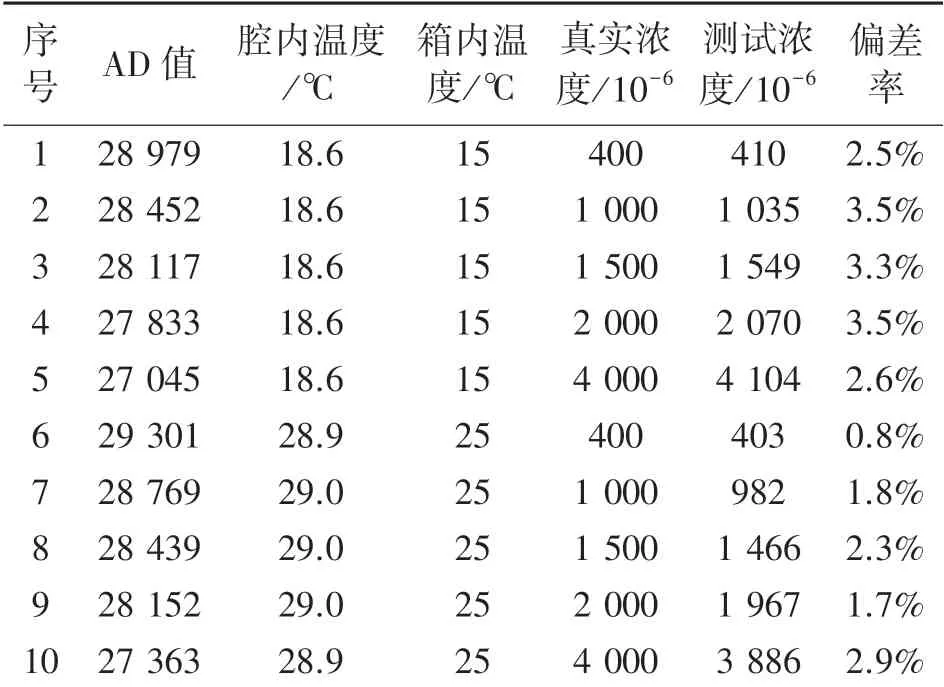
表3 浓度测试值和真实浓度的对比
3.2 不同次数拟合函数比较
实验中,利用MATLAB 进行曲面拟合时,分别采用双5 次(poly55),或一个5 次一个4 次(poly54),或双4 次(ploy44)多项式,所拟合曲面的确定系数与均方根误差如表4 所示。
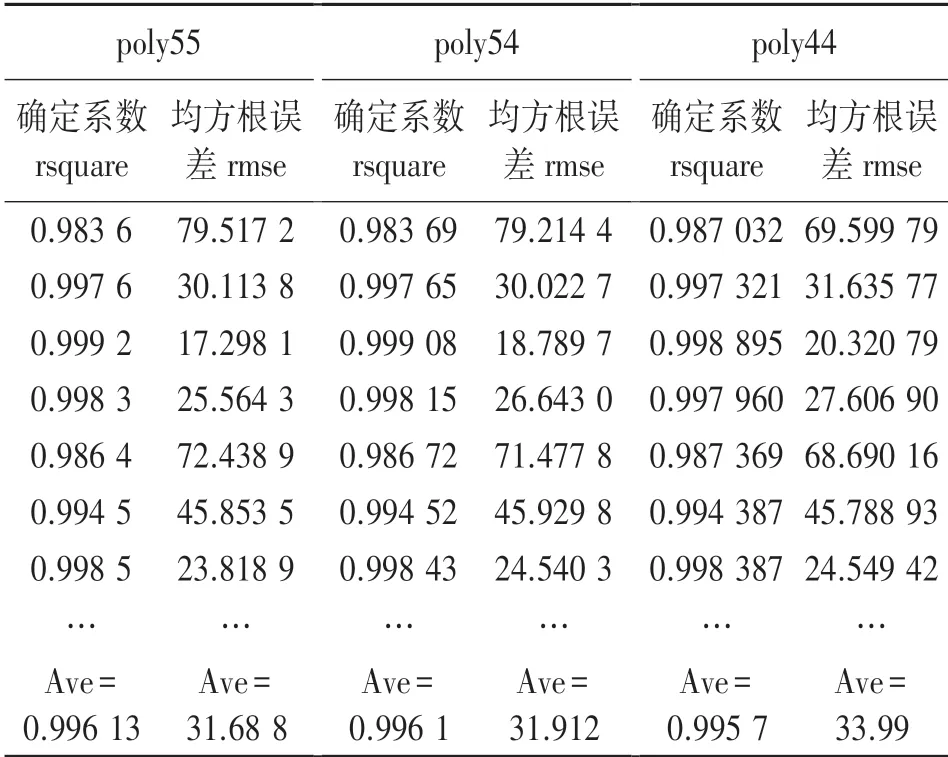
表4 确定系数与均方根误差对比表
表中最后一行为平均值。 随着系数的降低,确定系数平均值下降,均方根误差平均值增加,表明系数较高时拟合程度较好,但过高次多项式的拟合可能会产生过拟合和时间运行上的效率问题。MATLAB 最高的拟合次数为双5 次,即ploy55。 从实测效果上看,双5 次拟合并没有出现过拟合的状况。 在时间运行效率上,双5 次拟合速度也较快,因此选择ploy55 是较合理的。
3.3 与线性插值方案的对比分析
针对测得待标定传感器6 个数据点,即3 个箱内温度(5 ℃,20 ℃,35 ℃),2 个CO2浓度点(试验采用了400×10-6和2 000×10-6)时所对应的节点输出AD 值,本节评估线性插值法该较为简单直观的基准方案的性能,线性插值法生成三个不同温度下的浓度相对应于AD 值的变化直线(见图4),以此为基础,使用线性插值法拟合出其他温度时的变化直线。 图4 中三条实线为6 个数据点所生成的直线,从下到上分别对5 ℃,20 ℃,35 ℃时的浓度相对应于AD 值的关系。 两条虚线为使用线性插值法所得的5 ℃,25 ℃时的变化关系。 利用线性插值法所得拟合结果,计算出每个测试传感器的均方根误差,最后计算出平均的均方根误差为338.07。
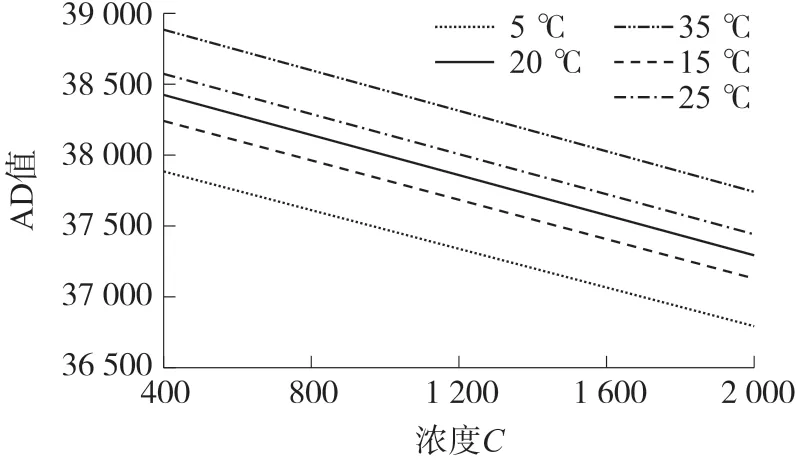
图4 线性插值拟合结果
从计算结果可以看出,采用曲面拟合的标定明显好于直接利用6 个点进行线性标定的结果。 由此可见,采用快速曲面拟合相较于线性插值的标定结果更为精确,在实际测量中可以获得更好的测量精度。
3.4 算法的主要特点及效果
基于曲面拟合快速标定算法的特点及效果主要有以下几点:①对一个新生产的待标定的传感器节点,只需针对3 个温度,测量每个温度下2 个CO2浓度点所对应的节点输出电压,共得到6 个数据点;标定的效率高,成本低。 ②算法具有较高的精度。 由于在曲面拟合的时候采用了大量的数据,使得这个曲面非常可靠,对于新测量的AD 值和腔内温度T,都能得到准确的浓度值。 ③通过采用标准气体校准的方式大大提高了红外气体传感器的准确性和一致性。
5 总结
针对NDIR 单通道CO2传感器提出了基于曲面拟合的快速标定算法。 首先通过对温度、电压、浓度(T,U,C)数据的采集,进行数据分析,得到N个CO2气体传感器特征拟合曲面,将这些曲面作为候选曲面;对新的待标定的CO2传感器,通过测定6个数据点,代入上述的候选曲面中,挑选出均方差最小的那个拟合曲面,作为该节点的CO2浓度估计模型,从而可以快速对CO2传感器进行标定。 试验结果表明该算法有较高的准确性,按照5%+50×10-6的精度来看,标定合格率高达99%。 另外,利用不同拟合次数拟合时的浓度估算误差结果表明,较高阶曲面拟合标定算法的计算精度高于较低阶的标定算法。 最后,将该曲面拟合算法与作为基准的通过6 个点作线性插值法进行了比较,曲面拟合算法具有较高的优越性。
