基于自适应事件触发和量化的时滞系统分布式滤波*

乔伟豪朱凤增彭 力

(1.江南大学物联网工程学院，物联网应用技术教育部工程中心，江苏 无锡214122；2.无锡太湖学院物联网工程学院，江苏省物联网应用技术重点建设实验室，江苏 无锡214064)

近年来，随着无线传感器网络(WSN)在环境监测，工业自动化，智能交通等多个领域的广泛应用，基于WSN 的分布式滤波问题受到越来越多学者的关注和研究[1-3]。 WSN 由多个传感器节点组成，在分布式滤波网络中，每个滤波器节点对应一个传感器节点，每个滤波器节点根据固定互连拓扑结构使用自身测量值及其邻居节点测量值来估计系统状态。 通过部分滤波器间的数据通信产生全局估计。与传统的集中式滤波相比，分布式滤波在传感器故障和传输约束方面具有更高的鲁棒性。 即使两个滤波器之间存在由于滤波器或传感器节点故障等原因导致的数据失效，依然可以从其他邻居节点获取信息，并且对系统的估计不会严重失真。

在关于分布式滤波问题的研究中，l2-l∞滤波方法针对系统模型中存在的不确定性及外部噪声等问题有很好的滤波效果[4-6]。 但分布式滤波在提高鲁棒性的同时也带来了能耗和通信资源开销增大的问题。 在某些无线网络中，需要尽可能的降低功耗和节约通信资源。 因此，事件触发机制是一个非常好的解决办法。 通过某种触发条件判断滤波器节点是否传递自身估计信息给邻居节点，能够有效降低信息传输频率，降低网络通讯负担。 由于这一优势，事件触发机制引起越来越多学者的关注，文献[7]提出了一种新型的事件触发方案来确定是否传输数据。 文献[8]提出了一个基于事件触发机制的时滞系统H∞滤波模型，文献[9]提出了一种多传感器网络的事件触发方案。 以上文献研究的事件触发阈值都是预设常数，事件触发阈值和通信网络数据传输速率相关，阈值固定导致事件触发机制无法根据系统变化动态改变数据传输速率，会造成通信资源浪费。 因此针对事件触发阈值的动态优化是非常具有研究意义的问题。 文献[10]研究了网络系统自适应事件触发机制下H∞滤波，提出了一种自适应触发机制来节约网络资源。 文献[11]研究了离散系统自适应事件触发机制下H∞跟踪控制。 文献[12]提出了一种改进的自适应事件触发机制设计方法。以上文献探讨了自适应事件触发的方案，但针对离散系统自适应事件触发机制下分布式滤波问题的研究不够丰富，并且设计的事件触发条件没有考虑邻居节点信息。 因此研究一种针对离散系统具有自适应阈值参数的自适应事件触发机制具有十分重要的意义，以便在解决滤波问题的同时保持令人满意的资源利用效率。

在WSN 中，由于传感器的测量精度有限且测量信号通过带宽有限的网络进行传输，因此，测量信号在传输前通常需要进行量化处理，但量化作用会导致量化误差的产生，对控制系统稳定性和性能产生影响，因此量化作用对控制系统的影响是一个值得研究的问题。 文献[13]提出了一种传感器信号量化模型。 文献[14]研究了带有量化的采样数据系统的H∞滤波。 此外，控制系统中时滞问题也普遍存在[15-16]，尽管由于5G 网络的兴起，网络传输的时滞问题得到一定程度上的解决，但是系统由于自身信息内部传输和外部干扰等因素依旧存在滞后现象，因此时滞系统稳定性问题仍具有重要意义。

本文研究了一类自适应事件触发机制下的离散时滞系统的分布式量化滤波问题，考虑了一种新型的分布式事件触发机制，触发条件通过滤波器自身估计值和最新传输数据以及邻居节点最新传输数据共同决定。 提出一种自适应事件触发参数动态调节方案，在保证滤波器性能前提下节约网络通信资源。考虑量化和时滞问题对系稳定性的影响。 设计了离散时滞系统满足性能指标的分布式量化滤波器，并利用LMI 方法，给出滤波器满足均方指数稳定并且满足给定性能的充分条件。

1 问题的描述

考虑一个具有n个节点的传感器网络，拓扑结构由有向图G＝(V，E，A)来表示，其中V＝{1，2，…，n}为节点集，为边界集，A＝[aij]n×n(aij≥0)为邻接矩阵。 如果有向图G存在一条从节点j到节点i的边界，那么有序对(i，j)∈E，并且aij＞0，并称节点j为节点i的一个相邻节点。 此外我们假定，对于所有的i∈V，aii＝1。 因此(i，i)可以认为是一条附加的边界。 节点i的所有相邻节点并加上本身，所构成的集合称为节点i的相邻节点集，记为Ni＝{j∈V:(i，j)∈E}。G的Laplacian 矩 阵 为W＝A-L，其 中L＝diag{li}且

考虑如下具有时变时滞的离散系统:

式中:x(k)∈Rl为状态向量；ω(k)∈Rp是外部扰动，属于l2[0，∞)；z(k)∈Rm为待估计信号，τ(k)代表时变时滞，且满足d1≤τ(k)≤d2；

传感器节点i(0＜i＜n)的模型如下:

式中:yi(k)∈Rq是传感器节点i的测量值，v(k)∈Rj是外部扰动，属于l2[0，∞)，系统矩阵A，Ad，B，M，Ci，Di都是已知的实矩阵。

考虑对数量化器f(·)，测量信号经过量化处理，有¯yi(k)＝f[yi(k)]，量化器f(·)是对称的，也即f[-yi(k)]＝-f[yi(k)]，对数量化器定义为:

定义Δf∈[-δδ]，通过文献[13]中的处理方法，f(·)可表示为f[yi(k)]＝(1＋Δf)yi(k)，故滤波器实际输入可表示为:

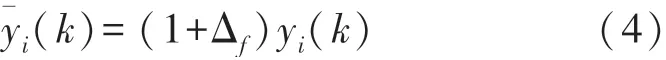
数据量化采用对数量化器，针对量化函数f(v)＝v可以将量化误差界定在[(1-δf)v(1＋δf)v]内[13]。

自适应事件触发方案如图1 所示，传感器节点i测量数据yi(k)，数据经过量化器量化后传输给滤波器节点i。 网络中每个滤波器节点从量化器和邻居滤波器节点获取数据。 滤波器节点中包含存储器，存储邻居滤波器节点传输的最新估计值，当新数据传输过来时，会丢弃旧有数据。 每个滤波器节点都通过事件触发条件判断最新估计数据是否向外传输。

图1 自适应事件触发系统框图

基于上述自适应事件触发设计方案，定义传感器节点i的自适应事件触发条件如下:

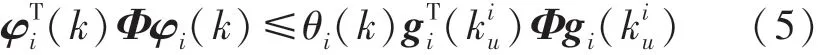
式中:Φ＞0 表示待设计的事件触发矩阵，k表示当前采样时刻，表示传感器节点i在当前时刻之前最新的事件触发传输时刻，u为事件触发时刻。 分布式自适应事件触发条件由滤波器节点自身最新传输的数据和邻居节点最新传输数据共同决定。

其中，φi(k)和gi()分别为:

自适应事件触发阈值参数θi(k)由以下自适应规则确定:

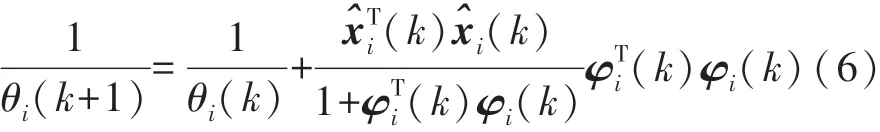
初始条件为θi(0)＞0。 自适应事件触发机制的事件触发参数θi(k)是根据式(6)的条件从θi(0)递减变化的。 滤波器事件触发参数的变化条件由最新发送值和当前估计值的误差大小决定。θi(k)的值越小事件触发越敏感。 参考文献[12]中针对连续系统设计的参数变化条件。

基于以上分析，针对传感器节点i设计的滤波器结构为:

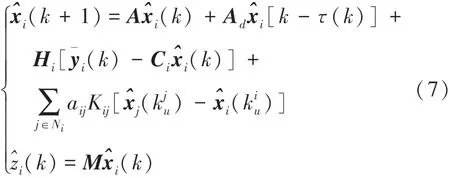
式中:(k)表示滤波器i对系统的状态估计，(k)是对信号z(k)的估计，Hi，Kij是需要确定的传感器节点i的滤波器参数。

令

ei(k)＝则节点i的触发采样数据可表示为:

为了方便表述，考虑网络中存在n个滤波器节点，定义k时刻误差估计向量时刻估计值和事件触发最新传输数据误差输出误差估计向量，事件触发参数初始值向量

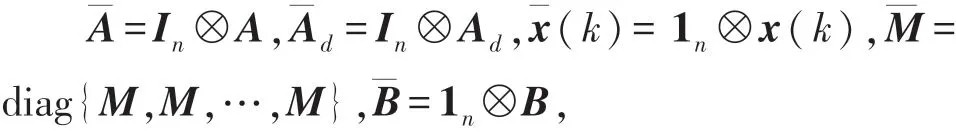
式中:张量符号⊗代表克罗内克积。

显然，如果j∉Ni，则是稀疏矩阵，可以表示为

定义:

根据式(1)和式(7)，增广滤波误差系统为:

式中:

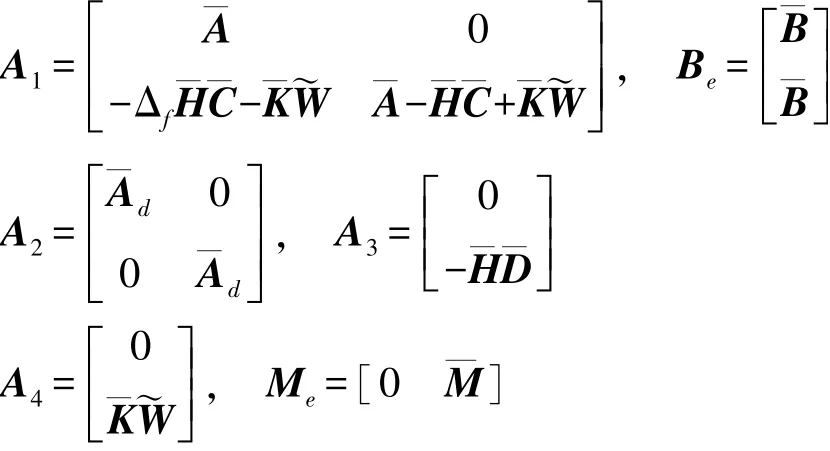
本文的目标是设计形式如(7)的滤波器，使得:①在外部扰动ω(k)＝0 的情况下，增广的滤波误差系统是均方稳定的。 ②在零初始条件下，滤波误差系统式(10)具有l2-l∞性能，即:

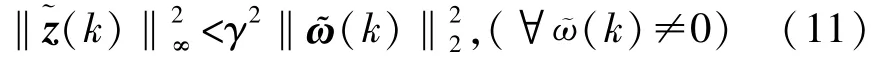
式中:

引理1[17]V(k)＝ηT(k)Pη(k)为Lyapunov 函数，如果存在实数λ≥0，μ＞0，υ＞0 和0＜ψ＜1 使得:

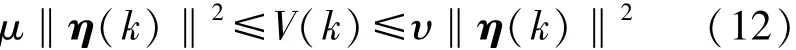
和

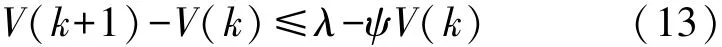
那么有

引理2[18]令Q＝diag{Q1，Q2，Q3，…，Qn}，其中Qi∈Rp×p(1≤i≤n)是可逆矩阵，若W∈Rnp×nq，X＝QW则有W∈Wp×q⇔X∈Wp×q。

引理3[18]如果存在一个对称矩阵P＞0 使得ATPA-P＜0，那么存在一个对称矩阵P和矩阵G使得:

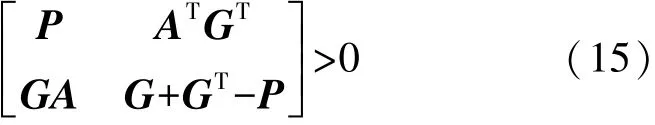
2 l2-l∞滤波分析

本节中，先给出使得滤波误差系统式(10)均方指数稳定并且具有l2-l∞性能的充分条件。

定理1给定γ＞0，如果存在正定矩阵P，S和矩阵，使得

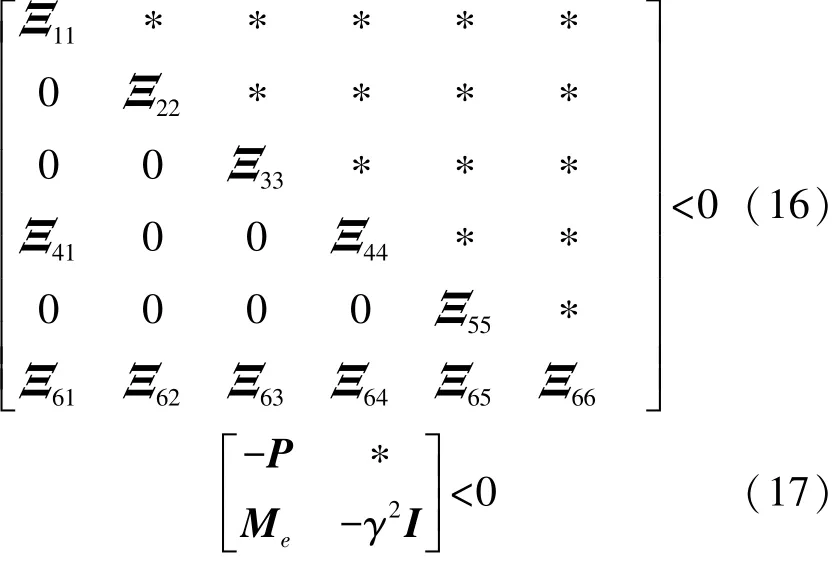
成立，那么滤波误差系统式(10)是均方指数稳定的，并且具有给定的l2-l∞性能。式中:

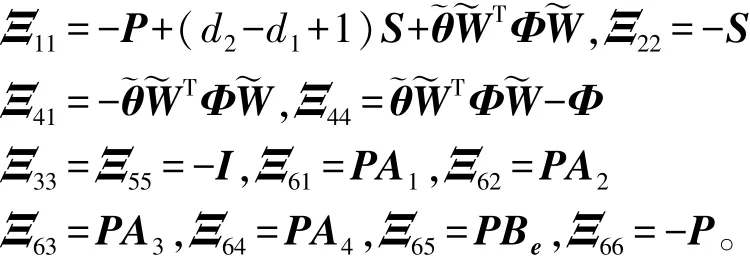
证首先要证明系统式(10)是均方稳定的，此时ω(k)＝0，v(k)＝0。

取Lyapunov 函数:

式中:P＞0，S＞0，则

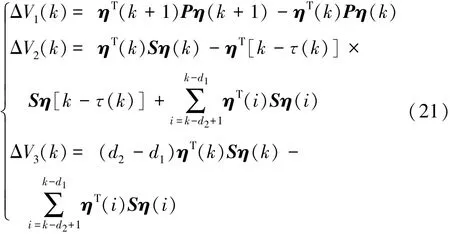
那么

式中:

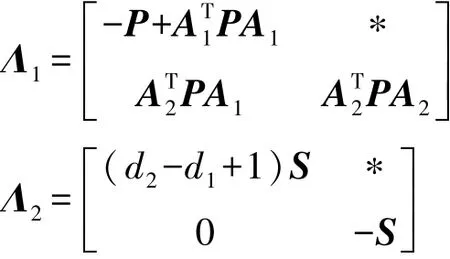
由Schur 补引理，式(16)隐含Λ1＋Λ2＜0，因此有:

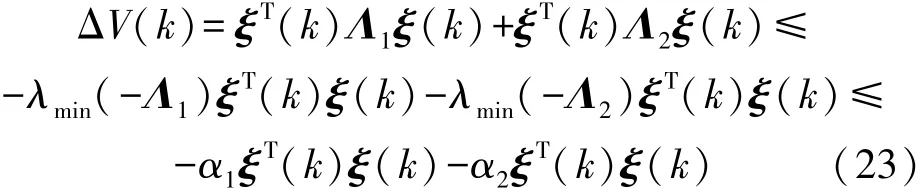
式中:0＜α1＜λmin(-Λ1)，0＜α2＜λmin(-Λ2)。

存在α1，α2同时也满足0＜α1＜λmin(P)，0＜α2＜λmin(S)那么

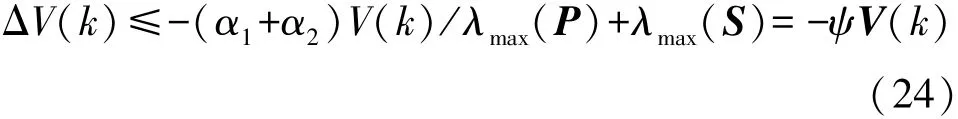
不难看出0＜ψ＜1。

那么由引理1，可以得到:

即系统式(10)是均方指数稳定的。

定义性能函数为:

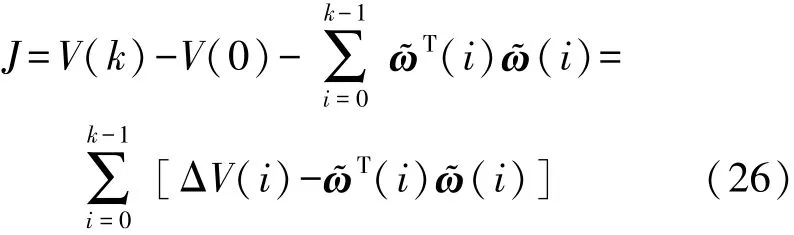
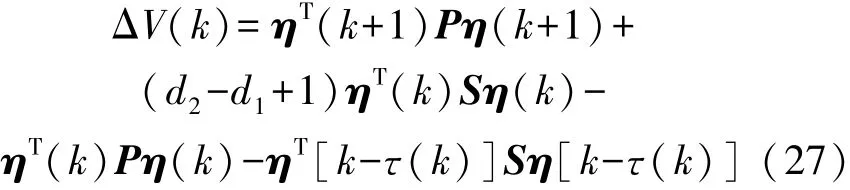
由式(5)可得:

考虑事件触发需要满足式(28)，自适应事件触发阈值参数θi(k)由式(6)所示自适应规则确定。所以θi(k)是单调递减的，当θi(k)为θi(0)时，事件触发频率最低，系统趋向于稳定。

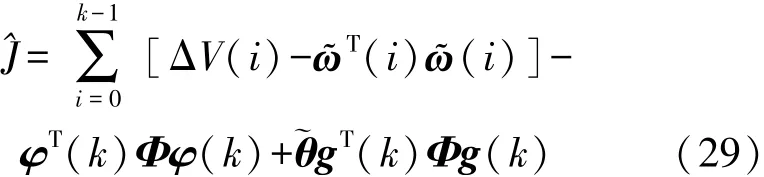
滤波器定义性能函数J的时候需要考虑事件触发条件(28)，故性能函数需要定义为式(29)的形式保证滤波器在事件触发情况下系统稳定。

令

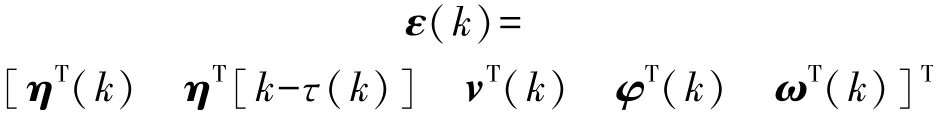
考虑式(28)和式(29)可得:

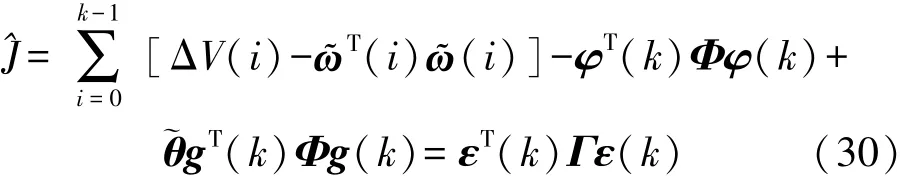
式中:

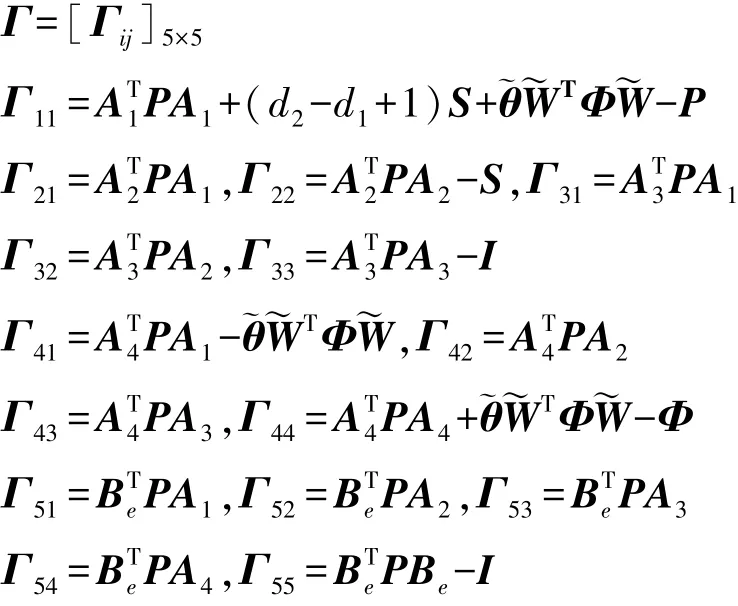
由Schur 补引理可知，式(30)和式(16)是等价的，所以即J＜0，所以

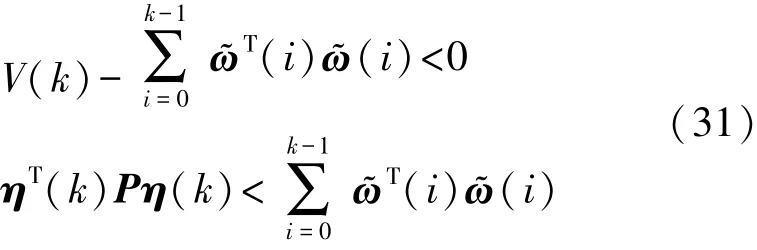
所以k＞0 时，有

由式(31)显然有

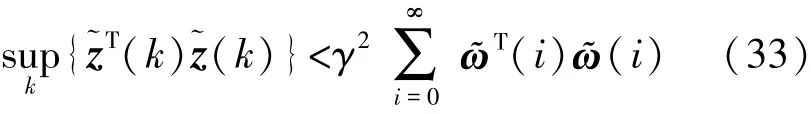
即:

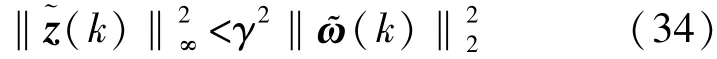
3 l2-l∞滤波器设计

在本节中利用上一节的定理给出滤波器的具体设计方法。

定理2给定γ＞0，如果存在正定矩阵对称阵P，S，矩阵使得式(35)和式(36)成立:

式中:

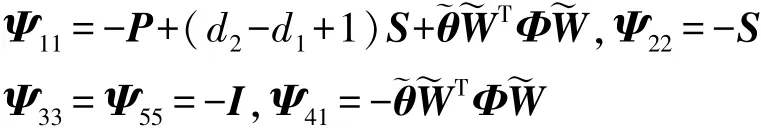
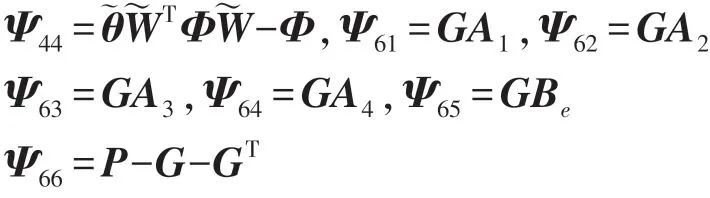
系统式(10)是均方指数稳定的且具有给定的l2-l∞性能。

证 将文中定义的变量代入式(16)，根据引理3定义的等价矩阵可证得式(35)和式(16)是等价的，证毕。

定理3给定γ＞0，由引理2 可得，如果存在正定矩阵对称阵P，S，矩阵V1，V2，V3，，使得式(37)和式(38)成立:

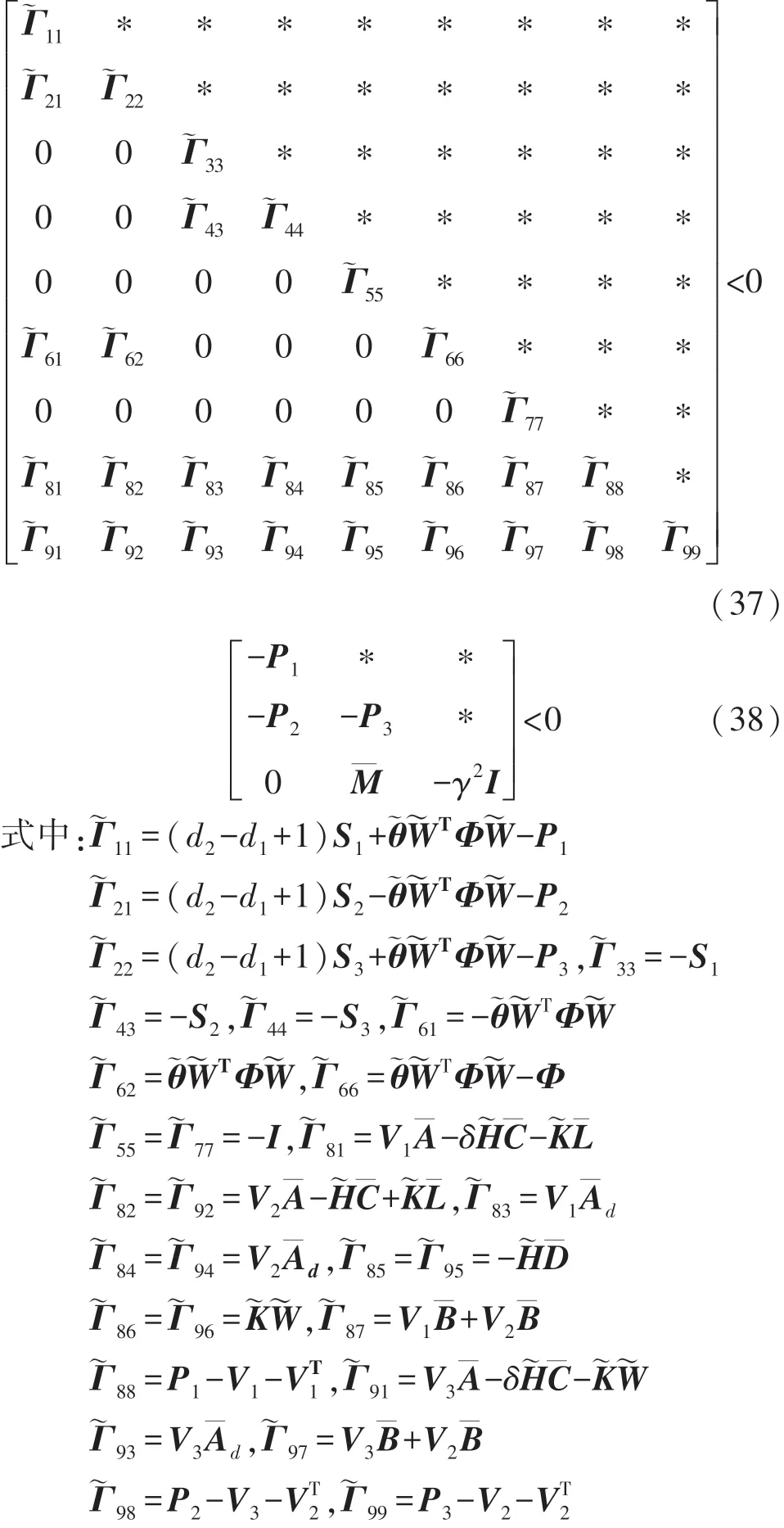
那么系统式(10)是均方指数稳定并且具有给定的l2-l∞性能。

证构造矩阵P和S为

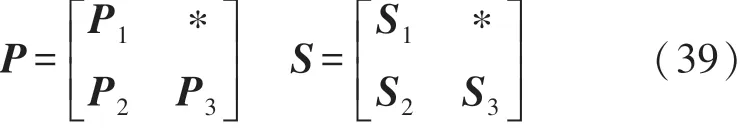
采用文献[10]所提出的变量替换法，即构造矩阵

将式(39)及式(40)代入式(35)可得式(37)，那么可取滤波器参数为根据文献[13]中方法可将Δf替换为δ，同时，由引理2 可知，¯H和¯K满足式(9)的约束，证毕。

4 数学仿真

论文研究了基于自适应事件触发的时滞系统分布式滤波问题，下面通过数据仿真验证算法的有效性。

假定分布式滤波器数量为4 个，即，分布式滤波器的拓扑结构为:

考虑离散系统参数如下:

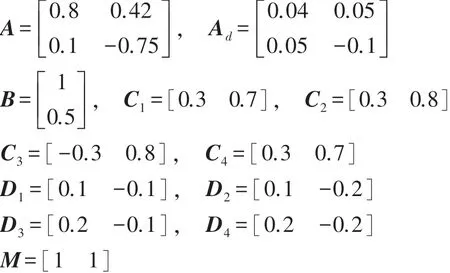
选取时变时滞τ(k)的参数d2＝2，d1＝1，自适应事件触发参数初始值θ1(0)＝0.6，θ2(0)＝0.5，θ3(0)＝0.4，θ4(0)＝0.3，量化密度p ＝0.666 7。

利用MATLAB 的LMI 工具箱可以求得最优γ＝2.658 9。 相应仿真结果如图2～图5 所示。

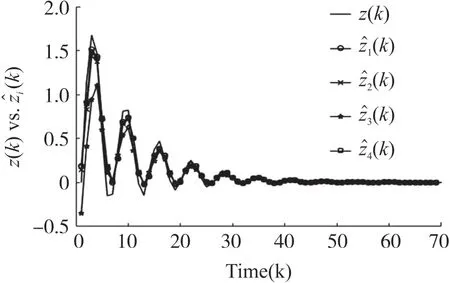
图2 系统实际输出和滤波器估计输出

图2 是系统实际输出和滤波器估计的比较图，图3 是滤波器事件触发频率图，图4 是自适应事件触发参数变化图。 通过上述仿真实例可以看出自适应事件触发方案在系统实际输出和估计误差较大时减小事件触发参数，增大事件触发频率，降低滤波器的估计误差。 系统趋于稳定情况，事件触发参数变化较小，减小事件触发频率，节约通信资源。 故自适应触发方案能够根据系统误差情况动态调节事件触发频率。

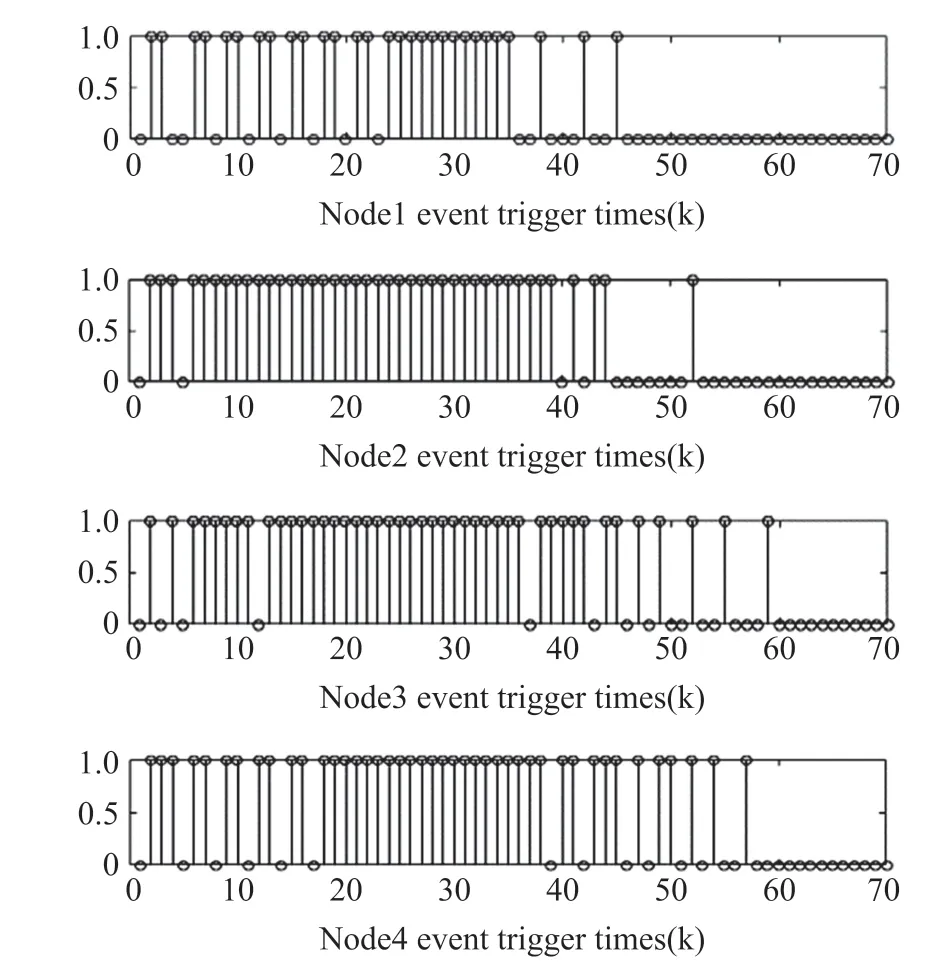
图3 各滤波器触发时刻

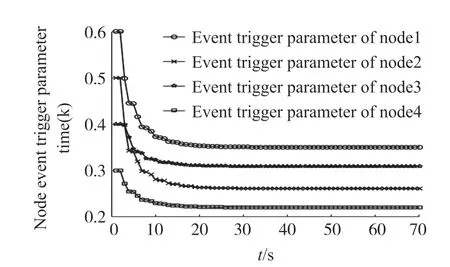
图4 事件触发阈值参数变化图

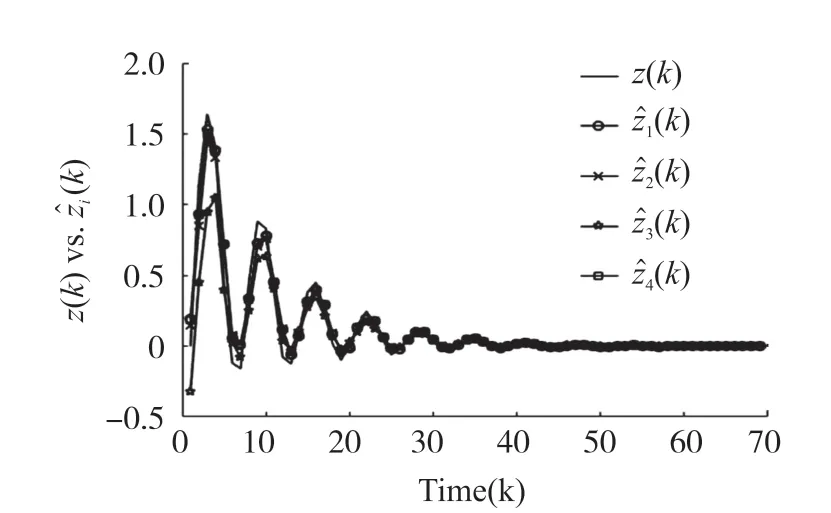
图5 无事件触发系统实际输出和滤波器估计输出

通过图2 和图5 比较可以看出，增加了事件触发机制的滤波器对系统的估计和没有事件触发机制下滤波器对系统的估计性能差距较小，但是事件触发机制能够节约较多的通信资源，故本文设计的事件触发机制能够在保证滤波性能的前提下节约较多的通信资源。 本文设计的自适应事件触发方案和文献[19]中的事件触发方案相比较可以看出，文献[19]中采用固定增加减少一定数值的自适应触发参数变化方案。 本文设计的自适应事件触发方案能够根据自身估计误差以及邻居节点最新触发值之间的误差动态调节事件触发参数，参数变化粒度更细，能够更为准确地调节事件触发频率，达到节约通信资源的目的。

5 结论

本文研究了基于自适应事件触发带有数据量化的时滞系统分布式滤波，讨论了自适应事件触发的设计问题。 设计了离散系统自适应事件触发方案，通过滤波器最新发送时刻估计值和当前时刻估计值的误差动态修改事件触发参数，使系统能够在保证滤波器性能前提下减少数据发送次数节约网络通信资源。系统中考虑了传感器精度和网络带宽有限带来的数据量化问题和系统内部存在的时滞问题。 在滤波器设计方面，利用李雅普诺夫稳定性理论和线性矩阵不等式方法，给出了分布式滤波器的满足l2-l∞性能指标的判据和滤波器参数的设计方法，最后通过数字仿真验证了设计方法真实有效。