基于均匀网格多层次B样条的CTA图像的运动向量场插值算法及加速实现

高强 ，鲍园，赵俊

1 上海交通大学 生物医学工程学院，上海市，200240

2 上海联影医疗科技有限公司，上海市，201807

0 引言

冠心病是心血管疾病中发病率、死亡率最高的，据统计在西方国家每年约有30%的人死于该疾病，并且我国也处于不断上升的趋势[1]。冠心病的早期诊断具有重要价值[1-2]。冠状动脉CT血管造影（computed tomography angiography，CTA）具有成本低、无创、准确性和敏感性高等特点，是继数字减影血管造影（digital subtraction angiography,DSA）之后监测和诊断心脏疾病的一种安全、可靠的方法[1]。CTA系统能成为检测心脏疾病的有效方法，得益于高速的球管旋转、宽大的探测器以及双源扫描等方式，减少了心脏的扫描时间，例如当今超高端的CT，可在0.28 s内完成360o的旋转[3]，从而提高了系统时间分辨率，提升了图像质量。但是每次扫描重建的图像，还可能会因心脏跳动频率比CT探测器采集频率高而产生运动伪影。

非刚性图像配准方法是解决上述问题的方法之一[4]，它主要包括心脏冠状动脉的特征点提取，生成运动向量场以及图像的灰度映射三部分[5]。其中，在生成运动向量场方面，样条插值方法可解决心脏冠状动脉运动自由度高、不确定性高等问题，是消除心脏冠状动脉伪影的主流方法[6～8]。薄板样条、（thin plate spline，TPS）插值方法是运动向量场插值方法的一种选择[8]，通过此方法可以找到通过所有控制点的最短路径，从而模拟心脏冠脉的运动轨迹，但是TPS属于全局性的配准方法，任意一个控制点发生变化都会对全局产生影响，配准精度并不是太高[6]。在执行效率方面，该方法运行时间过长，无法达到实时处理的要求。心脏冠状动脉运动是由心脏跳动与呼吸共同作用的结果，因此运动自由度比较高，需要对运动的局部性加以考虑。传统的B样条插值方法虽然在改变控制点时只会影响局部邻域，能够解决局部性变形的问题，但是随着物体模型变形程度的增加，其运动向量场配准的精度和执行速度也会下降。

我们提出了一种基于均匀网格多层次B样条的CTA图像的运动向量场插值方法，此方法可以从多尺度角度来控制网格的变化，一方面它从较稀疏的网格着手，能够模拟全局的弹性形变；另一方面它能够在上一层次的基础之上，逐渐步入较细的网格层次，由于控制点之间的间距变小，可以模拟局部的变形，从而提高配准精度。另外，利用分割矩阵的数学方法，可将插值时大量造成冗余计算的共享节点进行过滤，不仅兼顾了原有算法的配准精度，同时也提高了算法的执行效率。

1 方法

1.1 特征点集插值函数的构建方法

本研究提出的多层次B样条算法[9]是一种多分辨率多尺度的插值方法，它允许从离散的特征点集中拟合出三维自由形变的曲面。令三自变量目标控制点集：

P属于三维运动向量场V={(x,y,z,d)|0≤x＜m,0≤y＜n,0≤z＜l}内部。为了逼近P，构建一个均匀的三-三次B样条函数作为P的插值函数。令A是覆盖V区域大小为(m+3)×(n+3)×(l+3)的三维空间，Aijk网格是A空间网格中的某一控制点，那么P的插值函数为：

其中0≤t＜1。

曲面的逼近问题是确定运动向量场中的所有控制点的值A，根据式（2）可知函数值f(x,y,z)与数据点(x,y,z)邻域内的64个控制点相关，并且按照LEE等[9]提出的最小二乘法的思想来保证待求的V中每个控制点Aabc都在A范围内，最终通过以下方式计算出所有的控制点：

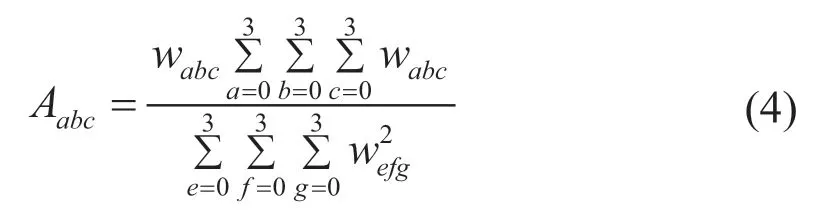
其中wabc=Ba(s)Bb(t)Bc(u)，wefg=Be(s)Bf(t)Bg(u)

1.2 运动向量场迭代插值过程

包含于空间网格A中的V可从多个尺度逐层插值，并可产生一系列插值函数fk，而它们的和就是逼近目标的插值函数，计算式为：

最稀疏的网格是由参考图像特征点与目标图像特征点的差计算得到的，并且可利用此网格的格点得到比较粗略的近似插值函数。后续细化后的控制格点可以进一步逼近和消除残差。当经过数次迭代得到目标尺寸的网格时，插值即可完成，参见图1的插值过程。

参考网格V代表运动向量场的初始位置，形变网格相当于运动向量场的位移量。起初网格比较稀疏，格点间的距离较大。经过每次迭代插值维度成倍增加，格点间距离成倍缩小，并且使用每次迭代生成的向量场（即参考网格与形变网格之和）通过式（2）得到的结果与目标匹配点的差作为下一次迭代的输入，这样反复N次迭代，当达到目标大小时结束。

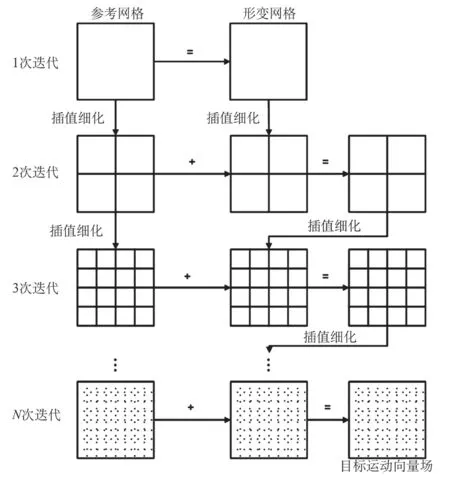
图1 MBS插值流程图Fig.1 Flow chart of MBS interpolation

1.3 分割矩阵插值方法

本研究采用了一种分割矩阵的数学方法，它允许对基于均匀网格的B样条生成冠状动脉的运动向量场进行迭代插值。TPS的插值方法忽视了冠状动脉的有效取值范围，对整个三维空间中所有坐标点进行全局插值，而本研究的方法可以只对提取的感兴趣局部区域进行插值。

其基本方法是将原有的B样条曲线分成左右两条曲线段，B样条矩阵[10]如下：

其中k=0,1,…,n-3且0≤t＜1，M为B样条基函数系数。假设一个B样条曲线P(t)是由控制点{P0,P1,P2,P3}构成的，我们将曲线二元细分，产生两条曲线PL(t)和PR(t)，并将原有t的[0,1)的取值范围划分为[0,0.5)和[0.5,1)。然后对这两条曲线段进行一系列的变换，最终得到基于控制点{P0,P1,P2,P3}插值点的表达式：

通过（7），我们可以知道PL(t)和PR(t)中存在被重复插值的点，即。这些重复点可以从任意一个曲线段中选取，最终可得到插值点公式：

1.4 插值算法优化方法

过滤掉分割矩阵插值方法中产生的重复的插值点是提高算法执行速度的关键。根据算法中的插值方法可以将待插值点的位置通过左右相邻的两个或者三个控制点通过式（8）计算得到，这样可以不用考虑控制点的空间维度只需将控制点集P按照一维的排列方式表示并额外复制3组相同的点集，统一定义为P1、P2、P3以及P4，其中点集中的每个元素以D来表示，而、'以及'是待插值的点集（见图2）。

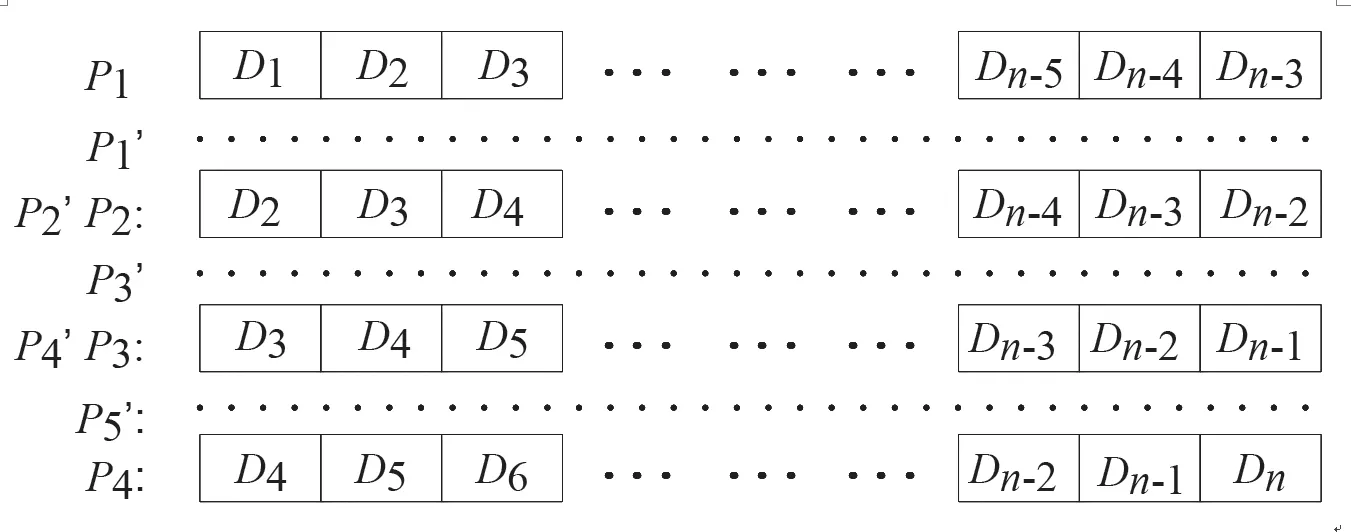
图2 待插值控制网格数据布局Fig.2 Layout of control grid data to be interpolated

每组点集按照同一点集中点与点之间的相邻关系进行纵向排列，这样可以对数据进行很好的并行处理，对于4组控制点集只需考虑彼此间对应位置即可。但是存在一个问题，那就是会出现大量插值点被重复运算导致计算资源的浪费（如图2中的第一列P2和P3中的D2和D3以及第二列P1和P2中的D2和D3），这主要是和分割矩阵算法特点有关。为了解决此问题，不妨先只对进行插值，当完成了当前维度的运算之后，再对以及做相同维度数据间隔长度的插值。根据三维空间的几何关系可知X方向插值数据间隔为1，Y方向插值数据间隔为X方向元素个数，Z方向插值数据间隔为XY平面的元素个数。通过上述方法得到如下结果：

（1）优化前总操作次数=31×插值数据长度，其中31次操作包括：12次读取操作、7次加法运算、7次乘法操作以及5次写入操作（以上操作次数可根据式（8）计算得到）；

（2）优化后总操作次数=31×插值数据长度－18×插值数据长度/数据重复周期，其中数据重复周期=维度长度×数据间隔。

因为维度长度和数据间隔只和当前插值数据的维度有关且相对不变，由此可见插值数据长度越大，提升性能就会越明显。

2 实验与结果

2.1 测试数据与环境

利用上海联影医疗科技有限公司320排CT拍摄的两套患者心脏的CTA数据对本研究提出的心脏冠状动脉运动向量场三维插值算法进行实验测试。本研究所使用的算法均在同一台工作电脑上实现，具体配置见表1。

表1 实验环境清单Tab.1 Experiment environment list

每套数据都包含一份CT重建后的投影数据，数据层厚为0.5 mm以及相关的从投影数据中提取并处理后的一套心脏冠状动脉特征点坐标数据。测试数据是通过心电图探测到心脏舒张期的信号后触发CT扫描并进行滤波反投影变换后得到的，其中表2、表3和表4中出现的Phase1、Phase2、Phase3和Phase4分别表示CT每旋转一定角度，通过上述方式所得到的数据。

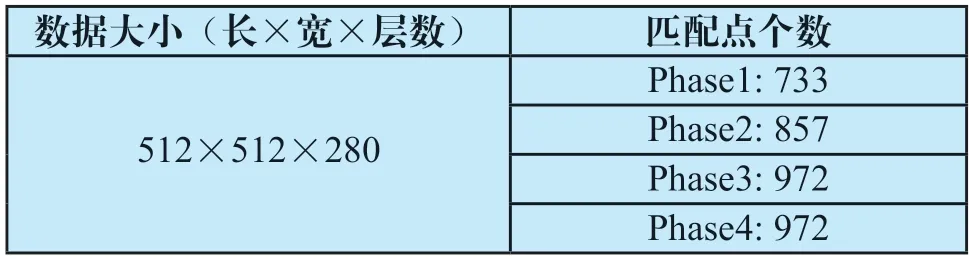
表2 原始数据信息Tab.2 Original data information

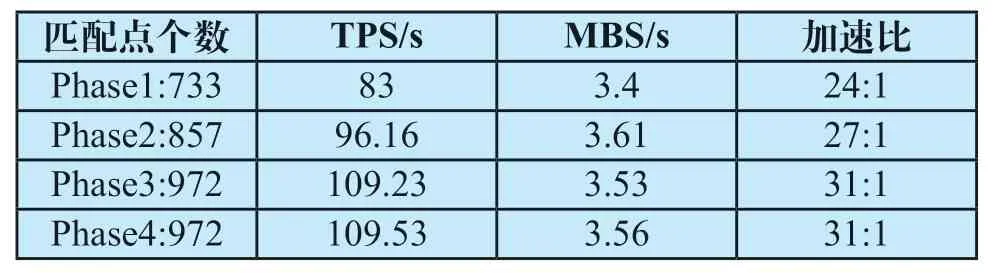
表3 TPS与MBS执行时间对比Tab.3 Time comparison between TPS and MBS

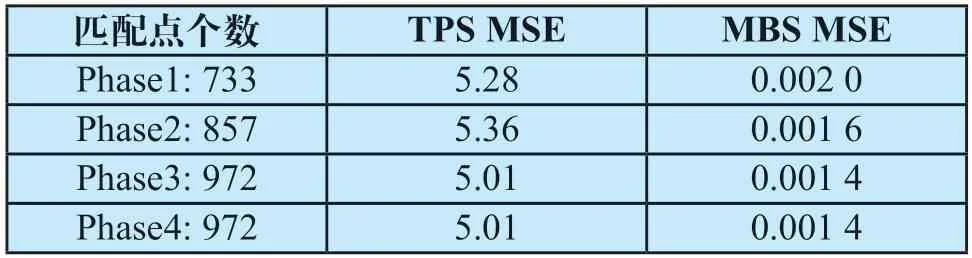
表4 TPS和MBS配准误差对比Tab.4 MSE Comparison between TPS and MBS

2.2 实验结果与讨论

本实验主要是对insight toolkit（ITK）提供的TPS算法与本研究提出的MBS算法在执行速度、均方误差（mean square error，MSE）以及校准后图像效果三方面进行对比。

（1）从执行速度来看，通过计算机性能计数器对两个算法的执行时间进行记录得到表3的结果，从中可以发现TPS随着匹配点的增加其执行时间呈上升趋势。而MBS算法的执行时间变化不大，不受匹配点个数的影响，并且在执行速度上明显高于TPS算法。主要原因是MBS的执行时间只和目标维度的大小以及迭代次数有关，即无论匹配点数是多少，都只需6次迭代从大小为16×16×12稀疏网格插值到516×516×284高密度网格。

（2）从配准精度来看，随着匹配点的个数增多，两种算法的配准精度都有所提高。薄板样条插值TPS配准精度一般，这很可能和它的全局配准性质有很大的关系，它不能像B样条一样进行局部性的微调。而MBS插值配准效果已经达到了小于1个像素的程度，针对匹配点集中Phase3匹配点的6次迭代的配准结果（见图 3），MBS首次迭代就已经达到了小于1个像素的精度并且每次迭代其精度都能够进一步提升。而TPS算法是通过线性方程组求解，在目标运动向量场的维度下进行插值得到的结果[11]，无法像MBS那样通过迭代在多个尺度上进行累积插值。因此，MBS算法在空间局部性调整控制点以及多尺度样条细化方面均具有优势。

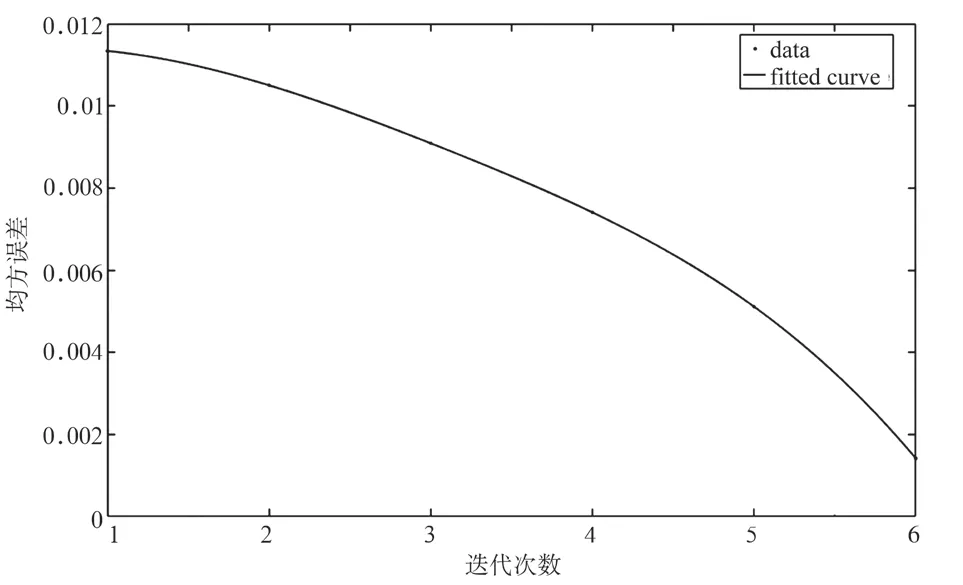
图3 MBS方法的迭代次数与配准精度关系图Fig.3 Relationship between iteration times and accuracy of MBS

（3）从处理后的图像效果来看（见图4），基于TPS插值的CTA图像中冠状动脉部分没有特别明显的处理效果，并且在图像整体上都有比较明显的拉伸，甚至在心室部位带来一定的伪影，这主要是因为TPS插值算法是在516×516×284整个图像空间坐标上进行插值的；而MBS插值算法不仅消除了校准图像中冠状动脉部位的拖尾，而且没有像TPS算法那样对整幅图像造成扭曲。并且通过图 5和图 6的运动向量场剖面图也可以看到TPS的运动向量场整体上都处于扭曲的状态，而MBS只有局部发生扭曲，其它部分没有明显的变化。

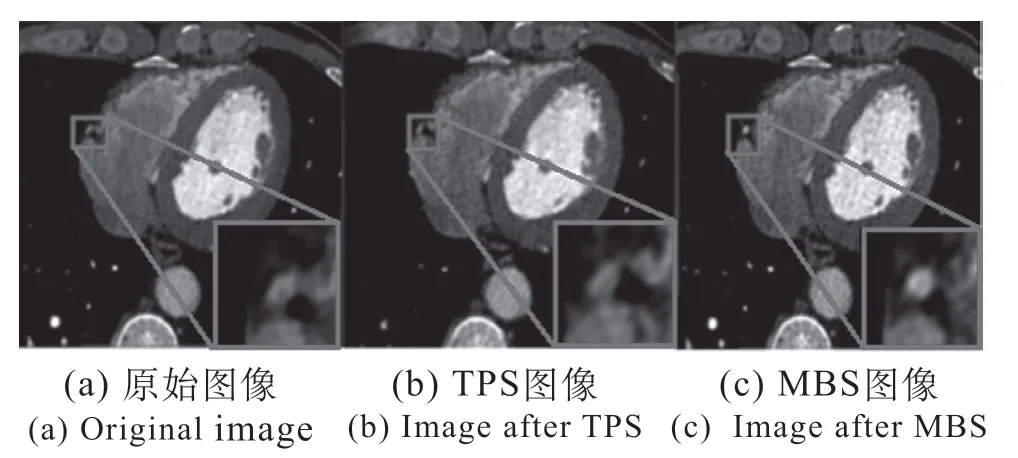
图4 图像对比图Fig.4 Image comparison result

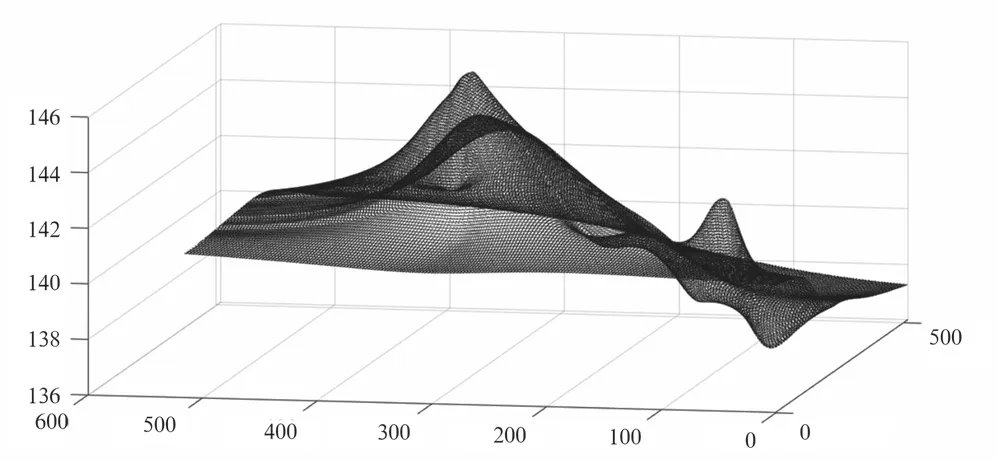
图5 TPS运动向量场剖面图Fig.5 Profile of motion vector field for TPS

图6 MBS运动向量场剖面图Fig.6 Profile of motion vector field for MBS

3 结论

本研究提出了一种基于均匀网格多层次B样条CTA图像的运动向量场快速插值方法，利用B样条函数本身的空间局部性以及多尺度迭代的插值方式使运动向量场能够产生较理想的形变，在配准误差方面达到了远小于1个像素的水平。另外，本方法采用分割矩阵的方式，将三维数据按照一维的方式进行插值，并利用插值点数值周期性重复，有效地过滤了重复的数据，极大地提高了算法的计算速度。实验证明，本方法对CTA图像去伪影有较好的效果，有较高的临床应用价值。

此外，为了快速得到高质量去伪影的CTA图像，需要将CT从多个角度采集到的数据进行处理，这个时候需要使用提出的方法以并行的方式对生成的匹配点集进行插值，这涉及到多线程开发的方法，未来可在GPU上开发此算法，进一步提高诊断效率和有效性。