基于最优系统能效的配电网规划方法
2021-04-08谢伟王哲斐蔡秋烨翁若方
谢伟,王哲斐,蔡秋烨,翁若方
(1.国网上海市电力公司青浦供电公司,上海 201700;2.上海四量电子科技有限公司,上海 201400;3.国网上海市电力公司嘉定供电公司,上海 201800;4.国网上海市电力公司,上海 200050)
0 引言
随着经济不断发展,节能减排的重要性越来越高。在用电量大幅增长的今天,电力系统成为提高能效的入手点之一,而配电网作为直接与用户侧接触的部分,其不合理的规划会造成显著的能效损失,导致大量额外能源消耗[1—3]。因此,对配电网进行合理的优化规划,对提高系统能效、电网运行的经济性和可靠性都有着重大意义[4—5]。
在传统的配电网规划中,其规划目标大都与经济性有关。例如,文献[6]中给出的配电网模型主要以建设费用最小为优化目标;文献[7]中的规划模型以配电网运行费用最小为规划目标;文献[8]中的规划模型考虑了配网网损,但也是归算成经济性指标进行规划。在当今的电网发展模式中,单纯追求经济性已经不再适用,更多的是要考虑节能减排。在已有的以提升电能传输效率为目标的配电网规划中,大都是关注配网网损的大小,例如文献[9]中给出的配网规划模型直接以减小配网网损为目标;文献[10]中的规划模型考虑了多种能效因素,但最终还是归算为对配网网损进行规划;文献[11]重点分析了分布式电源的接入对于配电网网损的影响。这些规划模型均难以全面反映整个配网的能效情况。
文中从配网系统能效入手,提出了基于最优系统能效的配电网规划方法。系统能效即在完成相同电力供应的情况下,所付出的能源最少。考虑到煤炭在中国的能源占比非常高,所以文中提出的配电网规划模型选取煤耗作为入手点,从一个相对宏观的角度对配电网进行规划,能够较为全面地考虑网损、分布式电源规划等能效因素。
在规划模型优化求解中,文中使用粒子群(particle swarm optimization,PSO)算法[12—15]的改进算法——惯性权重的粒子群算法(PSO-w)作为求解算法,其具有收敛快、寻优稳定的特点。制定了辐射网形态修正策略,保证了寻优结果的合理性。最后,选用IEEE 33节点算例进行模型和算法验证,并考虑了分布式电源的规划。计算结果表明,文中算法在收敛速度及寻优稳定性方面均有较高水平,规划结果稳定且合理,能够有效提升配网系统的能效。
1 基于最优系统能效的配电网规划模型
1.1 规划模型函数推导
文中提出的基于最优系统能效的配电网规划模型使用节点煤耗进行能效量化。节点煤耗的定义为:电力系统在用电侧每消耗单位电量的电能,发电侧以最节能的方式来满足负荷需求所消耗的标准煤的量[16](单位电能即1 kW·h,煤炭单位为g)。节点煤耗rn的表达式为:
(1)
式中:PLi为负荷的增量;Δfk(PGk)为第k台发电机以出力PGk运行所增加的煤耗量;NG为发电机总数。
配电网是一个辐射状的网络,一般情况下,功率流向是从变电站节点开始,顺着辐射状的网络流向网络末端的负荷,所以整个配电网的电能消耗可以用变电站节点流过的电能来表征。可以推知,变电站节点的节点煤耗即整个配电网的节点煤耗,且这个节点煤耗与配电网本身是没有关系的,因为配电网消耗一定的电量,然后这些电量需要消耗多少煤由上级的输电、发电部分决定。
文中模型是一个配电网规划模型,所以只考虑配电网的部分。因此,可以假设上级输电、发电部分情况不变,即配电网变电站节点的节点煤耗是不变的。根据式(1)可以得出,在节点煤耗不变的情况下,若想降低配电网煤耗,只需减小配电网消耗的功率即可,这是文中模型的关键。
流经配网的电能除了供给负荷外,在传输的过程中也会有电能损失。另外,文中模型考虑了分布式电源的存在,分布式电源作为一个电源,可以等效为降低了负荷。因此,配电网消耗功率为:
P∑=∑PL+∑PΔ-∑Pdg
(2)
式中:P∑为配电网向上级电网取用电能的总和;∑PL为配电网中的总网损;∑PΔ为配电网中的总负荷;∑Pdg为配电网中分布式电源的总出力。
综上推导,得到基于最优系统能效的配电网规划模型目标函数:
(3)
1.2 规划模型约束条件
(1) 辐射网约束。配电网必须是一个辐射状的、连通的网络。通常使用罚函数的方式来对此进行表达,即规划结果一旦不符合辐射状、连通性的要求,目标函数的值就会非常大,相当于否决了这个结果[17]。在计算过程中,并没有通过罚函数的方式,而是一旦检测出配电网规划结果不符合要求,就在计算结果的基础上进行改进,或者直接删除此次计算结果,其效果与罚函数相同[18]。
(2) 配电网中分布式电源总量的约束。如果配电网中接入了过多的分布式电源,会使电网的电压不稳定,从而影响配电网中的电能质量。因此对配电网中分布式电源的总量加以约束,表达式为:
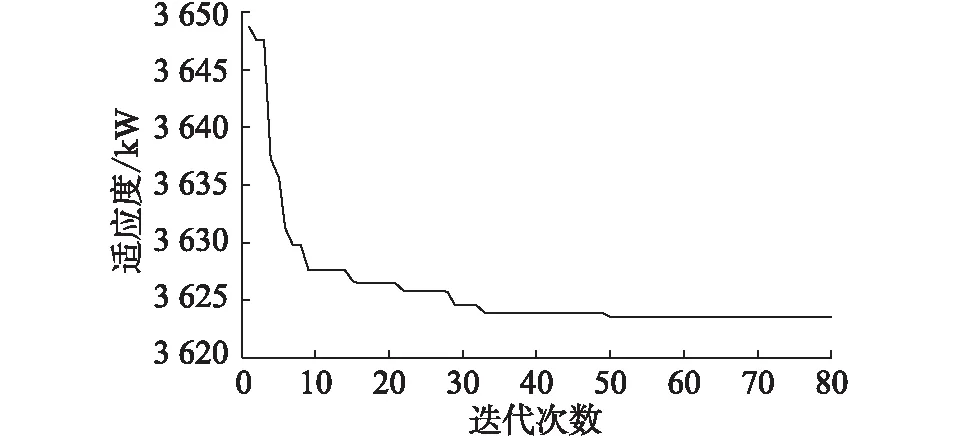
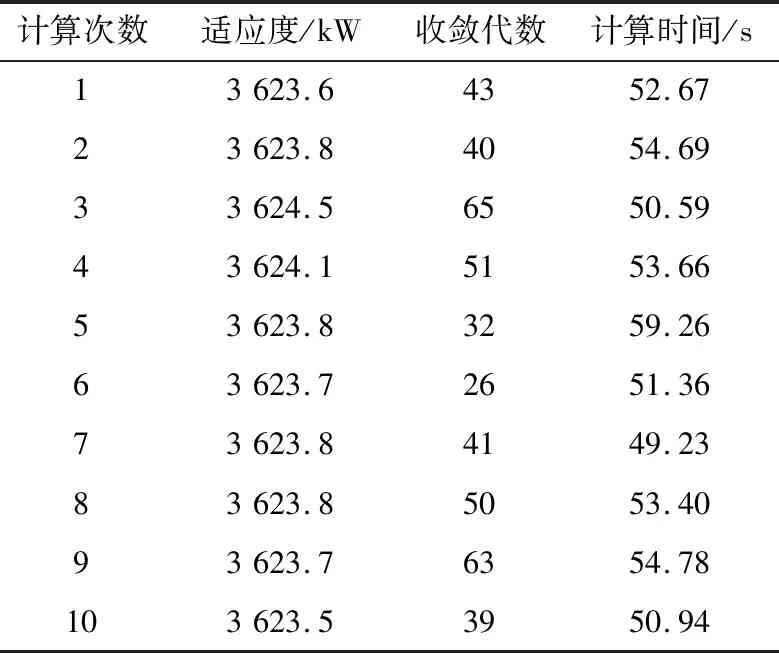
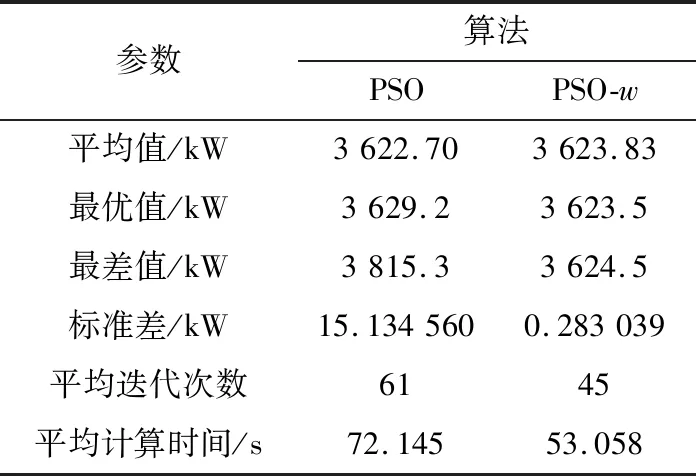
S∑DG (4) 式中:S∑DG为配电网汇总分布式电源的总量;SL为配电网中允许接入分布式电源总量的上限。 (3) 各节点分布式电源安装容量的约束。由于分布式电源大都不接受电力系统调度部门调度,所以如果某一节点接入的分布式电源容量过大,就容易造成事故。例如,形成反向潮流,导致配电网继电保护系统误动作。因此,需要对各节点分布式电源安装容量加以约束,其表达式为: SDGi (5) 式中:SDGi为节点i所接入的分布式电源的总量;Simax为节点i所能够接入的分布式电源容量的上限。 文中使用PSO-w算法进行模型求解。PSO-w在基本PSO算法的基础上加入了惯性权值w,其迭代公式为: vid(t+1)=wvid(t)+c1R[Pi(t)- (6) xid(t+1)=xid(t)+vid(t+1) (7) 式中:xi= (xi1,xi2,…,xid)为粒子在空间里面的坐标,i为第i个粒子,一共d个变量来表示d维坐标;vi= (vi1,vi2,…,vid)为粒子的速度,表示每一次的迭代过程中粒子所移动的距离;Pi为每一个粒子自身所到达的使结果最优的位置;G为全局极值;t为迭代的次数;c1,c2为加速系数;w为权重系数;R为随机数[19—20]。 w对PSO算法主要有以下方面的影响。当w取值变大时,粒子的移动速度也就相应增大,这样可以增大粒子的搜索空间,有利于发现新的更优解,但是也容易因为移动速度过快而错过最优解;当w取值变小时,粒子的移动速度也就相应减小,这样可以使粒子在搜索最优解时更为精细,即提高了粒子的局部搜索能力,但是这样容易造成局部最优。为了均衡以上因素,提出对w值做线性递减处理的方法,其计算公式为: (8) 式中:wmax,wmin分别为w的初始值与终止值;I为目前所迭代次数;Imax为提前设定好的最大迭代次数。 w可以扩大迭代初期的搜索步长,能够在搜索范围内进行较为广泛的搜索,然后慢慢缩小搜索的步长,使搜索变得精细化。这样既可以防止陷入局部最优,也可以避免错过全局最优解。 基础的PSO算法是针对连续函数设计的,其中的变量都是连续变量,但是有很多问题都是整数的问题,尤其是文中的网架规划。关于网架建设或者不建设,只有2种可能,所以实际上是一个“0-1”问题,因此采用离散二进制PSO算法[21—22]。 在离散二进制PSO算法中,所有的位置变量xid都只可以取0或1。速度变量不需要这样取值,而是可以转化为一个类似概率的问题:如果速度较快,那么位置偏向于取1,反之则偏向于取0。为了表达这种原理,使用模糊函数Sigmoid(x),其具体表达式为: (9) 当随机数R小于函数值时,则位置分量为1,反之则为0。 在配电网网架规划的结果中,需要对非辐射网络结果进行修正。检测配电网是否为辐射网的方法如下:以配电网的变电站节点作为根节点,然后搜索与变电站节点相链接的子节点,作为下轮搜索的根节点,以此类推。在搜索过程中,从图论的观点看,如果发现某个节点的入度不为1,那么该规划结果就不是辐射状网络,需要进行改进。 改进策略分为以下几类。 (1) 网络中存在回路情况。如图1所示,支路[5]、支路[6]以及支路[7] 3条支路构成了一个回路,这是不允许的,修改的方法为断开回路中1条造价较高且阻抗也较高的支路。 图1 网络中有回路情况Fig.1 The situation that has a loop (2) 孤点情况。如图2所示,节点5与网络中其他节点均无连接,这样的情况就是孤点情况。改进的方法为:从这个节点开始,向其上级节点进行搜索,然后比较这些节点与其上级节点之间支路的造价情况以及阻抗情况,按照低造价、低阻抗的选择标准,选择1条最优的支路把这个孤点连接到网络之中。 图2 网络中有孤点情况Fig.2 The situation that has isolated points (3) 孤链情况。如图3所示,支路[6]与网络其他节点都没有连接,这样的支路就是孤链。改进的方法为:首先要找出与这条孤链上的所有节点,搜索这些节点的上级节点,然后比较这些节点与其上级节点之间支路的造价、阻抗情况,按照低造价、低阻抗的选择标准选择1条最优的支路,把这个孤链连接到网络之中。 图3 网络中有孤链情况Fig.3 The situation that has a solitary chain (4) 孤环网情况。如图4所示,支路[5]、支路[6]以及支路[7] 3条支路形成了一个环网,且与网络中其他节点均无连接,这样的环网就叫做孤环网。改进的方法为:首先使用孤链的处理方法,把孤环网连接到配电网网络之中,然后以高造价、高阻抗的选择标准,把环网中的1条支路断开。 图4 网络中有孤环网情况Fig.4 The situation that has a lone ring 选用IEEE 33节点算例[23—24]来进行计算和分析。此系统是一个有着37条待选线路的待建配电网,电压等级设定为12.66 kV,整个配电网有功负荷总和为3 715.0 kW,无功负荷的总和为 2 300 kvar。其规划前的结构如图5所示,其中,1节点作为配电网的变电站节点,其他节点都是负荷节点,均是分布式电源可以安装的位置。 图5 33节点待规划配电网网络结构Fig.5 33-bus distribution network structure to be planned 设置分布式电源总安装容量的最大值为 200 kV·A,单台分布式电源的容量设定为50 kV·A。PSO算法的参数中,加速系数c1,c2取2,惯性权值wmax,wmin分别取1.2,0.8,最大迭代次数设置为80次,种群规模(粒子数)设置为40。 3.2.1 配网规划分析 通过PSO算法对算例进行求解,得到规划结果。由于算例中是37条待选线路,根据配电网辐射性、连通性的要求,必须选择其中的32条线路投建,因此有5条线路不投建。对于分布式电源规划,每台分布式电源所对应的号码就是分布式电源所投建的节点号码。配电网规划结果如表1所示。 表1 配电网规划结果Table 1 Distribution network planning results 由表1的规划结果可以看出,网架规划部分结果是非常稳定的,可以确定5条不投建支路号分别是 7,9,14,28,32。由此可以得到网架规划结果,如图6所示。 图6 网架规划结果Fig.6 Grid planning results 由表1可得到以下结论。第一,在算例中设置了分布式电源总容量为200 kV·A,单台分布式电源容量为50 kV·A,而所有的规划结果都是投入了4台分布式电源,所以每次的规划都是尽可能地增加分布式电源的投入。第二,虽然分布式电源的选址结果略有不稳定,但是几乎都分布在16,17,18,31,32,33这几个节点上面。从图6的网架规划结果可以看出,分布式电源都是分布在配电网网络末端,这样的规划结果是非常合理的,因为分布式电源规划在网络末端可以最大限度地减小系统网损,从而减小配电网从上级电网取用的总功率。 3.2.2 配电网规划效果 适应度收敛过程如图7所示,可以看出,在接入分布式电源的前提下,在寻优过程中,配电网的向上级电网取用电功率从3 650 kW下降到3 625 kW,说明在确定分布式电源接入容量的情况下,优化算法是有效的。 图7 适应度收敛过程Fig.7 Fitness convergence process 但是由于这里的电功率绝大多数是负荷功率,而分布式电源最大接入量仅占不到6%,所以仅总电功率下降并不能够有效反应算法的优化作用。考虑配电网优化对网损的影响,配电网网损的变化趋势如图8所示。可以看出,配电网网损在优化后下降了约15%~20%,算法优化效果显著。 图8 配电网网损变化曲线Fig.8 Curve of distribution network loss 使用文中所述的PSO-w算法以及离散二进制PSO算法,按照上述参数取值,对33节点算例进行10次计算,计算结果如表2所示。 表2 计算结果Table 2 Calculation results 对上述计算结果进行数据统计处理,并加入普通PSO算法的计算结果作为对比,结果见表3。 表3 计算结果数据统计Table 3 Calculation result data statistics 由表2和表3可得到以下结论:(1) PSO-w算法稳定性是较好的,因为10次独立计算的适应度值都非常接近,说明优化结果基本一致。PSO-w算法的最优值与最差值之间仅差了不到万分之三,并且标准差也降到了0.28,体现了算法的稳定性。(2) PSO-w算法的效率高,运行速度较快,从统计结果来看,平均迭代次数为45次,最大迭代次数为65次,最少为26次,收敛速度较快,平均计算时间小于1 min,运行速度较好。(3) PSO-w算法在结果稳定性、收敛速度以及计算速度几个方面均明显优于普通PSO算法。 文中从系统能效入手,提出基于最优系统能效的配电网规划方法。该方法以节点煤耗为入手点,较为全面地考虑了配网网损、分布式电源出力、位置等能效因素。算例验证表明,文中算法可以有效提升配网系统能效,收敛快且稳定性高。配电网规划结果合理,验证了文中配电网规划模型和求解算法的有效性,为配电网规划提供了一个可行方案,具有一定的借鉴意义。2 基于PSO-w算法的优化求解方法
2.1 PSO-w算法
xid(t)]+c2R[G(t)-xid(t)]2.2 离散二进制PSO算法
2.3 辐射网形态修正策略




3 算例分析
3.1 参数设置
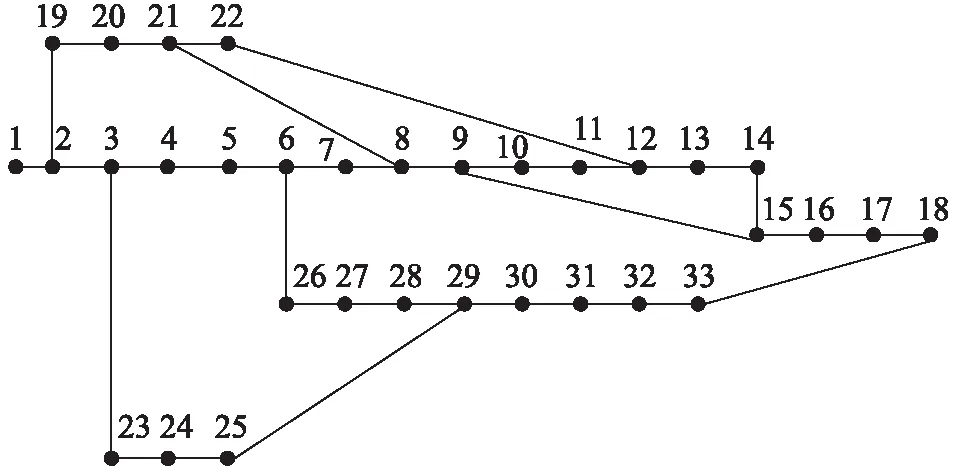
3.2 配电网规划分析



3.3 算法性能分析
4 结语
