晶闸管电子负荷在孤网频率振荡抑制中的应用

陈辉，韩连山，李成博，刘伟航

(南京南瑞继保电气有限公司,江苏 南京 211102)

0 引言

电力系统在正常运行时，电网中的发电功率与用电功率相等，电网的频率保持稳定[1]。发电机具备一定的调节能力，当负荷功率发生变化时，发电机可以通过调速系统调整发电功率，维持功率平衡，保持频率稳定[2]。然而，处于孤岛运行的电网的发电机装机规模有限、旋转备用较小[3]，其调节能力有限[4]。当因故障跳闸、大型冲击性负荷退出等导致大功率负荷突然消失，发电机调节能力不足时，电网频率快速升高，发电机超速保护、高周切机、低频减载交替动作，严重时甚至会造成黑网事件[5]。这种现象在2～4台机组的孤网系统中尤为突出，孤网系统中发电机和负荷的数量少，功率调节性手段也相对较少，因此出现甩负荷时更容易引起事故扩大[6]。

为应对电力系统突然甩负荷造成的频率异常，解决方案有改造发电机机网协调系统、配置稳定控制系统、配置高周切机、增加低频减载保护以及采用蓄电池储能系统等。其中，机网协调系统需要对原发电机进行改造，提高发电机的调节能力，但仍需发电机在正常运行期间留有一定的旋转备用[7]。稳定控制系统、高周切机以及低频减载系统是电力系统安全稳定运行三道防线的概念[8]。这些策略通过切除部分发电机、部分负荷甚至部分电网的方式维持系统功率平衡，但在孤网系统以及微电网系统中，由于发电机、负荷颗粒度加大，难以通过二、三道防线匹配发电-负荷功率，电网仍面临一定失稳风险。储能系统作为新兴的电力系统调节手段在资源配置优化和系统稳定方面具有一定的效果，但蓄电池造价昂贵、寿命短、充放电次数有限、维护工作量大，因此储能在孤网中作为调节性电源应用时具有一定局限性[9]。电子负荷装置可应用于厂矿企业电网，在优化大型负荷投退策略、补偿功率缺额、平衡三相有功以及配合机组黑启动等方面具有显著成效[10—11]。

文中提出采用基于晶闸管控制的电子负荷装置解决电力系统由于甩负荷而造成的失稳问题。介绍了电子负荷的基本原理和控制策略，并针对企业电网频率振荡的问题，进行了针对性分析。结果表明，电子负荷能够快速平滑地调节功率，在电网一次调频、频率阻尼抑制方面效果显著。

1 电子负荷结构与原理

常规电子负荷系统采用机械开关分组投切的方式实现，如图1(a)所示。其中，ui，ia分别为电子负荷电压、电流，R为电阻。常规电子负荷虽然价格相对低廉，但存在机械开关响应速度慢、分合闸操作周期长、开关故障率高等缺点。文中采用反并联的晶闸管阀组替代传统的机械式开关，通过调节晶闸管的触发角实现负荷功率调整。

在大功率电力电子产品中，应用最多、最成熟的电力电子器件是晶闸管和绝缘栅双极型晶体管(insulated gate bipolar transistor，IGBT)。其中晶闸管的典型应用是高压直流输电换流阀以及静止无功补偿器等，而IGBT的典型应用是柔性直流输电换流阀以及直流断路器等。相比而言，IGBT造价昂贵、控制复杂且故障率高。电子负荷采用晶闸管控制，在性能和工程应用上更具性价比[12]。

在工程实际应用中，为了减小晶闸管导通时的电流变化率、限制晶闸管端短路引起的短路电流，需要在回路中串联电感L，如图1(b)所示。

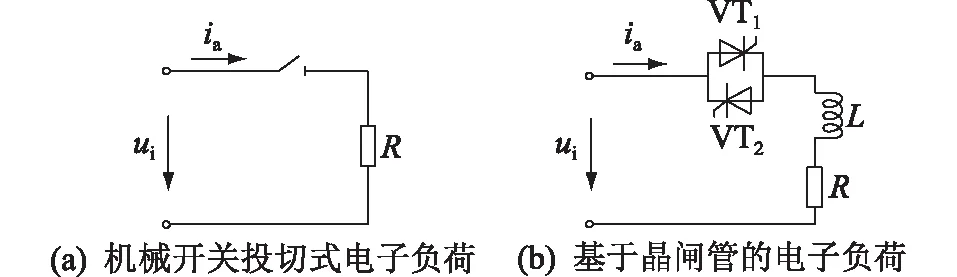
图1 电子负荷装置原理Fig.1 Principle of the electronic load device

晶闸管阀组的设计借鉴了静止无功补偿器中晶闸管及其阻尼回路的设计[13—14]，晶闸管触发和监视电路采用高压自取能方式。电子负荷工作时的电压和电流关系如图2所示。其中，α为晶闸管触发角；θ为晶闸管导通角；ug1，ug2分别为VT1，VT2的触发脉冲。电子负荷根据系统控制需求生成功率指令，通过闭环调节α满足控制需求。

图2 电子负荷晶闸管控制逻辑Fig.2 Thyristor control logic of electronic load

假设系统电压有效值为U，则触发角为α时，装置电压、电流为[9]：

(1)

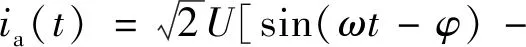
(2)

其中：

(3)

φ=arctan(ωL/R)

(4)

则装置电流有效值为：

(5)

其中，α，φ，θ满足：

(6)

可见，随着α的变化，电子负荷的电流不同，其运行功率也随之改变。运行功率为：

(7)

不同α下的运行功率点对应关系如图3所示。

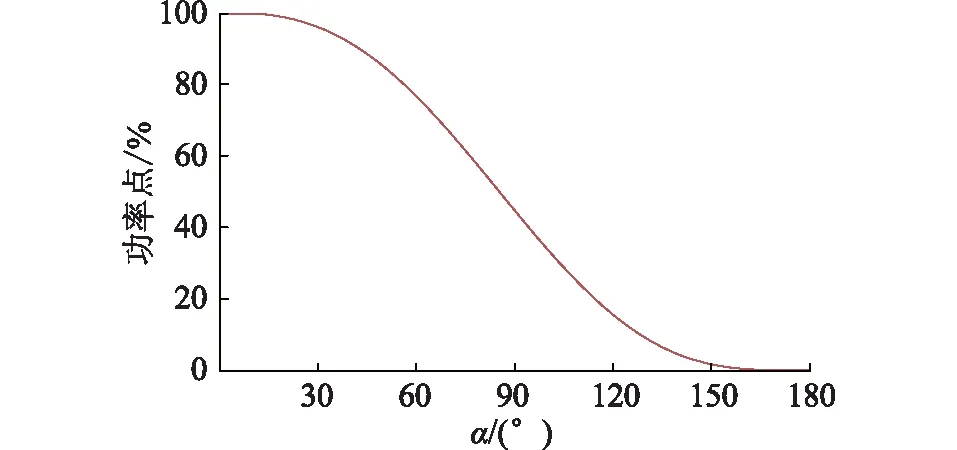
图3 α与功率运行点对应关系Fig.3 Correspondence between α and power operating point

用晶闸管代替常规的机械式开关，可以将负荷的响应时间从数秒级减少至数十毫秒级，控制精度从数兆瓦提升2～3个数量级至千瓦级。因此采用电子负荷可以实现诸多常规负荷无法实现的功能。需要说明的是，电子负荷作为一种调节性负荷或紧急备用负荷，在正常情况下不运行，因此一般不承担生产任务。

电子负荷由于采用晶闸管相控的工作原理，工作时其电流呈断续状态，会产生一定的谐波和感性无功，可通过配置一定数量的滤波器实现谐波滤除和寄生感性无功补偿。

2 电子负荷控制策略

2.1 整体控制策略

电子负荷装置的主要控制手段是控制α，最终通过改变功率运行点实现冲击负荷补偿、频率振荡抑制等高级功能[10]。电子负荷装置的整体控制如图4所示，包含5级模块，分别为功率差额、比例积分(proportional integral,PI)、限幅、α换算及阀控模块。

图4 整体控制策略Fig.4 Overall control strategy

其中，核心控制部分采用经典的PI控制，该环节把输入的功率差值Δp经过PI运算，输出给限幅环节。α换算的作用是把输入的功率指令折算为晶闸管的α。由图3可知，对于每个确定的p有且仅对应一个α。然而p和α呈非线性关系，无法采用解析法得到指定p下的α，因此采用多项式数值拟合的方式代替，即：

α=a0+a1p+a2p2+a3p3+a4p4+a5p5

(8)

多项式的项数越多，拟合的曲线越精确，多项式的系数a0～a5取决于整体功率的大小。阀控部分的功能是把计算出来的α通过光电转换等环节最终作用在阀组上，该环节实际上是一个延时环节，用于模拟实际硬件设备的信号延迟。

2.2 功率差额环节

图4中功率输入指令Pref，负荷平衡系统的实际有功功率Pact以及频率阻尼辅助控制输入指令Pfreq构成了功率差额环节。不同应用场景下，电子负荷系统有不同的控制模式，不同控制模式下Pref的选择如图5所示。手动功率模式时，Pref由运行人员通过人机界面直接给定；功率跟踪模式时，Pref为功率跟踪点在一段时间内的平均功率;稳控协调模式时，Pref通过与稳控通信获取。需要注意的是，模式切换时，Pref的切换缓慢平滑，避免给系统带来冲击。

图5 不同控制模式下Pref的选择Fig.5 The choice of Pref in different control modes

2.3 频率阻尼抑制环节

频率阻尼控制一般作为控制器的辅助功能,通过在主控制回路上叠加一个控制信号实现阻尼抑制[15—16]。图4中Pfreq的生成方式见图6。

图6 频率阻尼抑制框图Fig.6 Block diagram of frequency damping suppression

图6共由6级环节组成，分别为频率差值、低通滤波、2级超前滞后、矫正以及最终的限幅。其中，频率差值环节根据输入的频率值fact，设定的频率上限fmax和设定的频率下限fmin得到，表达式为[17]：

(9)

电力系统正常运行时，允许频率在一定范围内波动，此时发电机自身的调节能力可以满足稳定调节的要求，因此在此期间电子负荷系统不参与调节；当频率越过限定范围时，电子负荷系统参与调节。

滤波环节和超前滞后环节用于对输入的频率差值信号进行移相处理。通过调整移相角度实现频率振荡阻尼控制。Kfreq为矫正环节系数，即单位频率偏差下对应电子负荷装置的功率矫正值。限幅环节限定频率辅助环节输入到主逻辑回路的功率幅值。

在相同的工况下，频率限定范围的大小、矫正系数的大小以及超前滞后的相位调节都会影响频率阻尼效果，具体参数设定应根据实际系统需求确定。

3 案例分析

广西某电解铝企业为解决生产过程中突然丢负荷而引起的频率振荡问题，新建了一套60 MW电子负荷系统。根据该企业电网的模型，基于实时数字仿真系统(real time digital simulation system,RTDS)搭建一仅有2台发电机的小型孤网系统，分析电子负荷在甩负荷过程中频率振荡抑制效果。每台发电机的装机容量为132 MV·A，功率因数为0.85，配置4组固定负荷，负荷总容量为250 MV·A，其中有约100 MW的不稳定负荷。RTDS试验模型如图7所示。

图7 RTDS试验模型Fig.7 RTDS test model

α为150°，90°，25°时，电子负荷装置的电流如图8所示。由图8可知，α越小，对应的电流越大，相应的运行功率也越大。

图8 不同α下的iaFig.8 ia at different α

研究不同参数下，电子负荷系统的频率抑制对电网频率的影响，在运行过程中突然切除100 MW负荷，形成电网频率扰动进行研究。案例1为未投入电子负荷，案例2～案例7具体参数如表1所示。

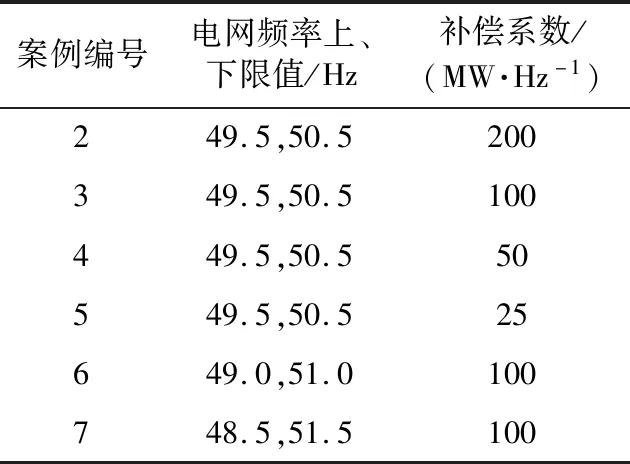
表1 电子负荷频率振荡抑制功能参数Table 1 Frequency oscillation suppression function parameter of electronic load

图9对比了投入电子负荷前后(分别对应案例1、案例2)电网频率、电子负荷输出功率的变化情况。由仿真结果可知，未配置电子负荷时，由于电网负荷丢失过大，超出发电机的调节能力，导致电网频率开始振荡，且振荡幅度有增大趋势，最终可能使电网频率崩溃、电网解列或直接黑网。而投入电子负荷后，电网频率振荡得以抑制，并最终将电网频率稳定在一个新的状态，防止了电网频率崩溃。

图9 电子负荷投入前后对比Fig.9 Comparison before and after electronic load is input

当电子负荷的补偿系数不同时，对电网频率振荡抑制的效果也有所区别，对比如图10所示。在频率振荡抑制的速度方面，较大的补偿系数可以更快速地抑制频率波动；在稳态功率方面，补偿系数越大，最终新平衡状态电子负荷输出的稳态功率也越大。由于电子负荷系统以消耗电网功率实现功角稳定，较大的补偿系数会对电网带来较大的能源浪费。在实际工程中，应根据不稳定负荷的大小、频率振荡抑制的时间要求等具体确定补偿系数。

图10 不同补偿系数下频率振荡抑制效果对比Fig.10 Comparison of frequency oscillation suppres-sion effect under different compensation coefficients

电网频率的上、下限值会对电子负荷的效果产生影响，图11为不同频率限值条件下电子负荷的动作曲线。

图11 不同频率限值下频率振荡抑制效果对比Fig.11 Comparison of oscillation suppression effect under different frequency limits

由图11可知，电网频率上、下限差值越小，电子负荷的响应越积极。一次调频实际上是有差调节，当系统的实际频率超出范围后，电子负荷才会以差值为基准进行反向调节，因此频率限值越宽，相同频率波动下频差越小，电子负荷的响应越慢。对于企业电网而言，频率限值的设定只需满足正常生产要求即可。

4 结语

文中从结构、原理、控制策略及仿真分析方面对电子负荷装置进行了研究。首先建立了基于晶闸管的电子负荷装置的数学模型，分析了采用晶闸管作为控制元件实现功率连续调节的可行性；然后给出了电子负荷装置的控制策略及其在频率振荡抑制方面的控制模型；最后根据实际工程需求，在RTDS 平台上分析了不同装置及电网参数下电子负荷的实际应用效果。文中工作为电子负荷的工程应用奠定了理论基础。