利用“主线”破解立体几何中的垂直问题
2021-04-08罗红
罗 红
(云南省蒙自市第一高级中学 661199)
立体几何在高考中是必考内容,垂直的证明与应用是考题中的热点,对于学生而言,都希望在高考中这道大题能得满分,但是有很大一部分学生不但不能得到满意的分数,还容易陷在此题中耗费过多时间,尤其是遇到证明线线垂直、线面垂直和面面垂直时,有的学生看似在证明,其实不得其法,思路混乱入不了门,完成不了证明.
在立体几何垂直的证明中,无论是线线垂直、线面垂直还是面面垂直,归根结底是要证明线面垂直,下面给大家介绍一种方法:“一主线,多垂直”.所谓“一主线”指的就是到底要用哪条线来证明它与另一个面垂直;“多垂直”指的是我们在图形中能找到的垂直,两者合二为一就能快速解决问题.
一、高中数学几何中常见的几种垂直
二、线面垂直
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.

例1如图1,已知PA⊥BC,AB是⊙O的直径,C是⊙O上不同于A,B的任意一点,过点A作AE⊥PC于点E.
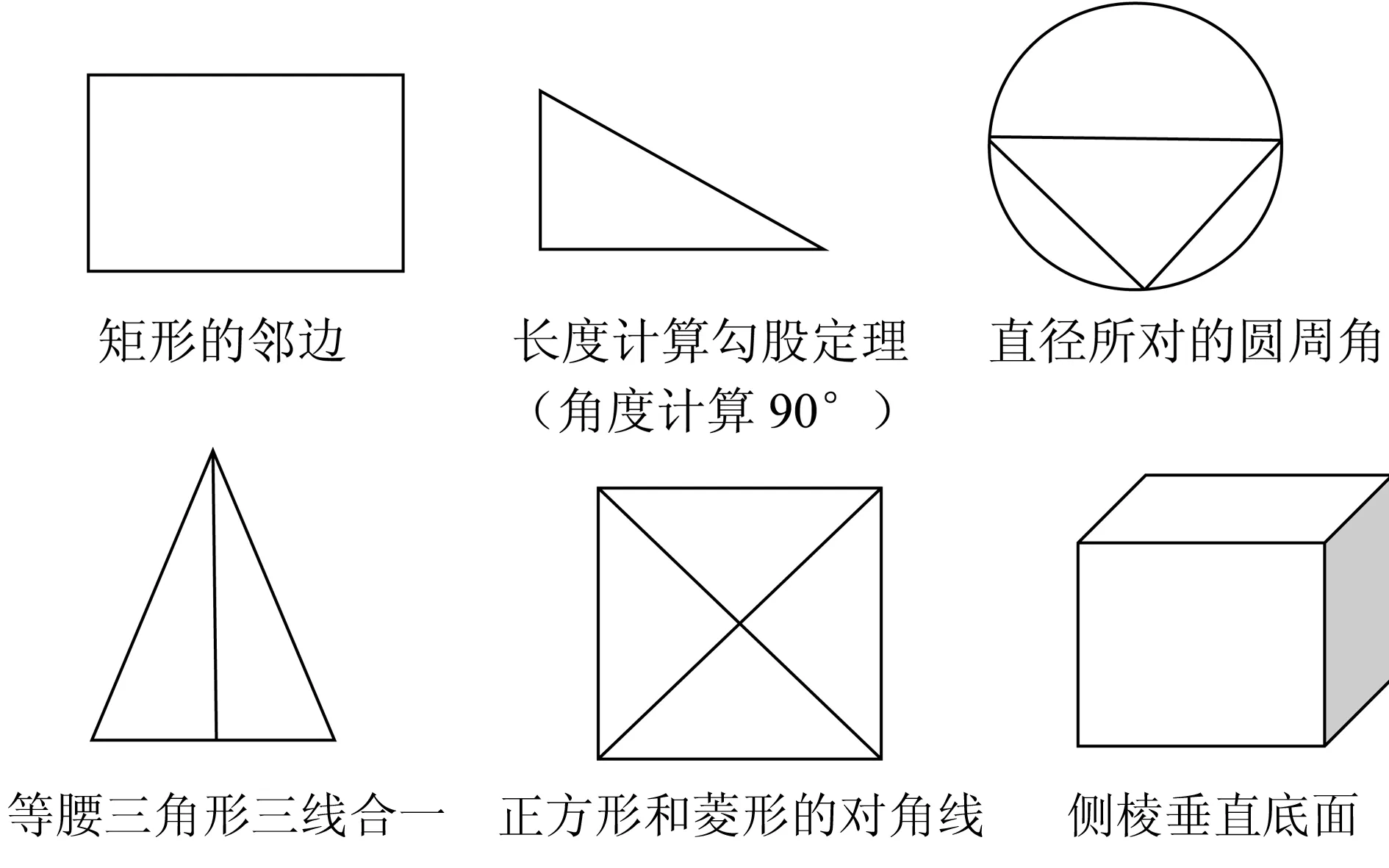
求证:AE⊥平面PBC.
分析要证AE⊥平面PBC,只需要证明AE垂直平面PBC中的两条相交直线即可,题目中已有一条AE⊥PC,另一条要去找垂直多的地方,观察图形,发现底面有一个直径所对的圆周角,左边还有题设给的垂直PA⊥BC没有用,整体“重心”在左方和下方,所以考虑应该找AE⊥BC.
证明因为AB是⊙O的直径,所以BC⊥AC.
因为PA⊥BC,PA∩AC=A,所以BC⊥平面PAC.
因为AE⊂平面PAC,所以BC⊥AE.
因为AE⊥PC且PC∩BC=C,所以AE⊥平面PBC.

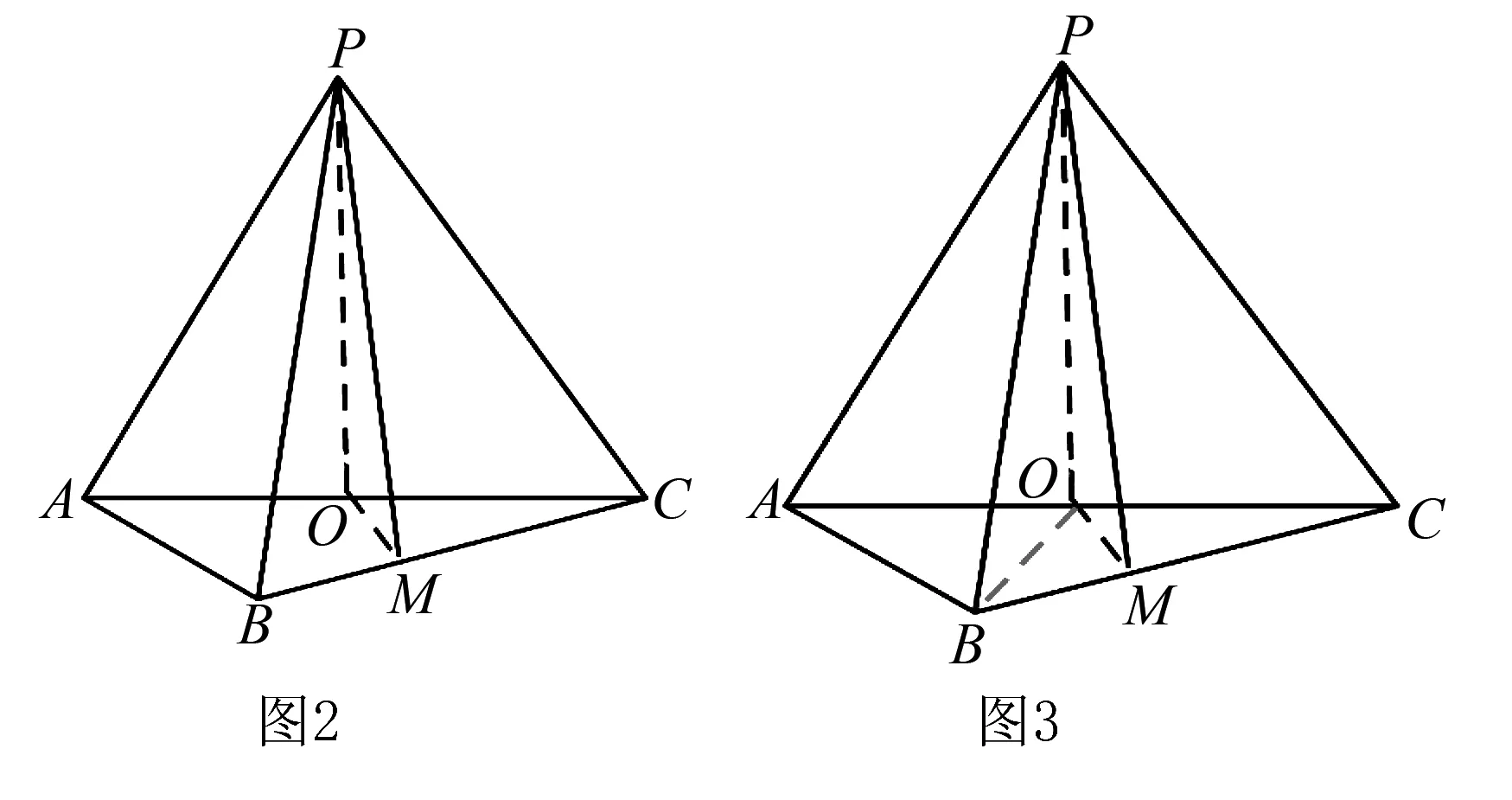
(1)证明:PO⊥ 平面ABC;
(2)若点M在棱BC上,且MC=2MB,求点C到平面POM的距离.
分析第(1)问的证明题目中没有给现成的垂直,但是给了很多的线段长度,这种类型的题要注意数据,看有没有等腰三角形三线合一,有没有满足勾股定理的逆定理,从而得出直角.通过观察,我们发现PA=PC,O为AC的中点,所以有PO⊥AC,要证明PO⊥平面ABC,还差一条线,从图上看底面ABC中还剩下AB,BC,PO与AB,PO与BC是异面直线,显然不是这两条,所以我们要重新找一条能够和PO构成一个平面,又能充分利用已知数据,自然联想连接OB,容易证得OP2+OB2=PB2,从而得出PO⊥AB.
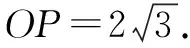
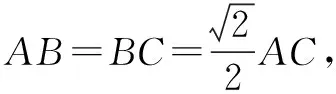
由OP2+OB2=PB2,知OP⊥OB.
由OP⊥OB,OP⊥AC,知PO⊥平面ABC.
三、线线垂直
如果一条直线垂直于一个平面, 那么这条直线与此平面内的任意一条直线都垂直.
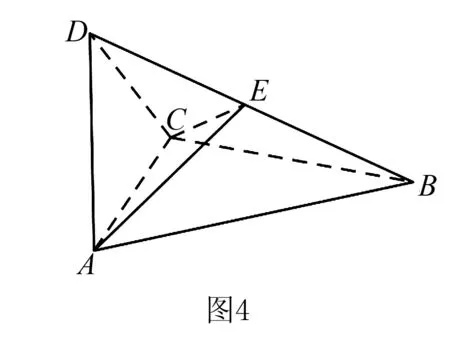
例3(2017年全国Ⅲ卷文数19题)如图4,四面体ABCD中,△ABC是正三角形,AD=CD.
证明:AC⊥BD.
分析要证明线线垂直多用线面垂直,需要找出一条线和一个面,所以要区分到底哪条线是主线,哪条线要放在平面内,在做题之前可用不同颜色标明两条线.下面来看两条线谁的垂直会多一些,因为△ABC是正三角形,AD=CD,出现了等腰三角形和等边三角形,很自然地联想“三线合一”,所以取AC的中点O,连接DO,BO,这样就构成了一个平面,而且还有两个垂直,如图5,所以AC是主线,BD要放在平面内.
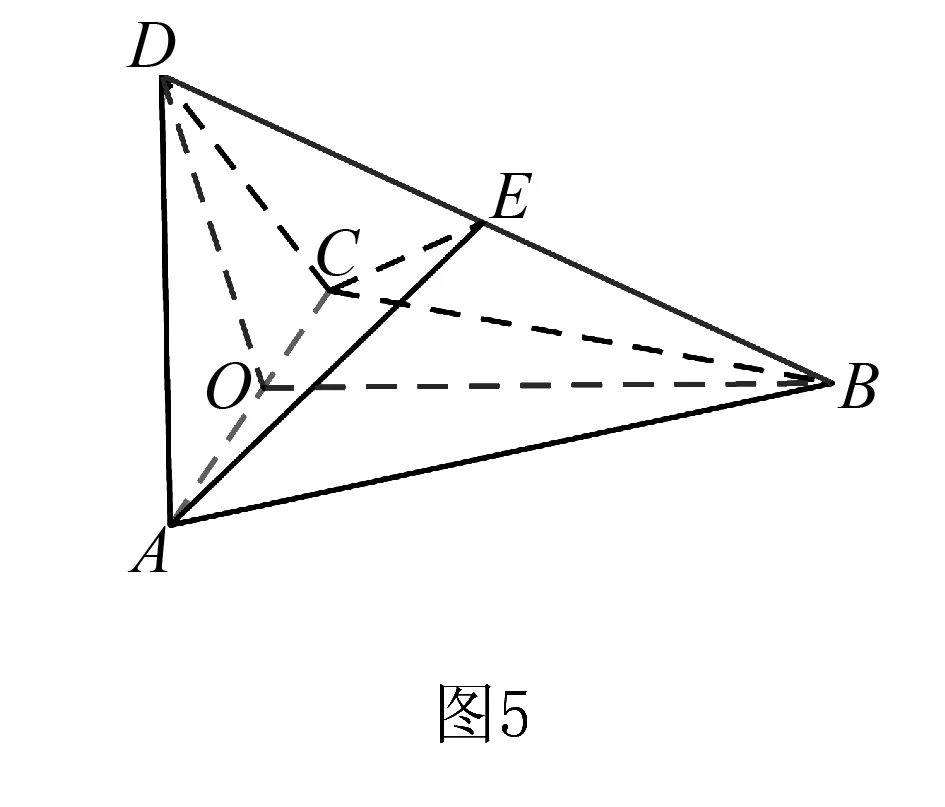
证明取AC的中点O,连接DO,BO.
因为AD=CD,
所以DO⊥AC.
又由于△ABC是正三角形,所以BO⊥AC.
又DO∩BO=O,从而AC⊥平面BOD,故AC⊥BD.
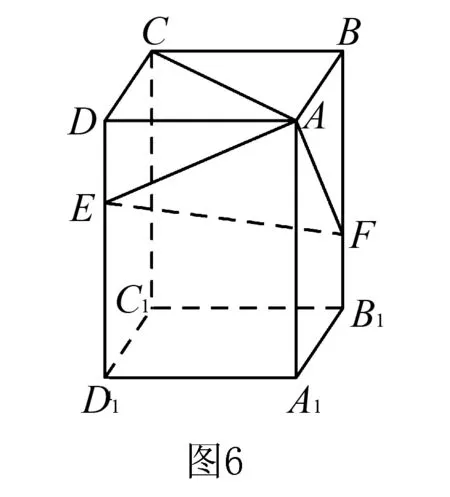
例4(2020年全国Ⅲ卷文数)如图6,在长方体ABCD-A1B1C1D1中,点E,F分别在棱DD1,BB1上,且2DE=ED1,BF=2FB1.
证明:当AB=BC时,EF⊥AC.
分析AC是长方体上底面的一条对角线,因为AB=BC,所以上底面是正方形,两条对角线互相垂直,显然AC和EF比较,AC能找到的垂直更多,所以AC是主线,要把EF放在一个平面内,至此,主线与平面已区分开来,只需构造平面即可.
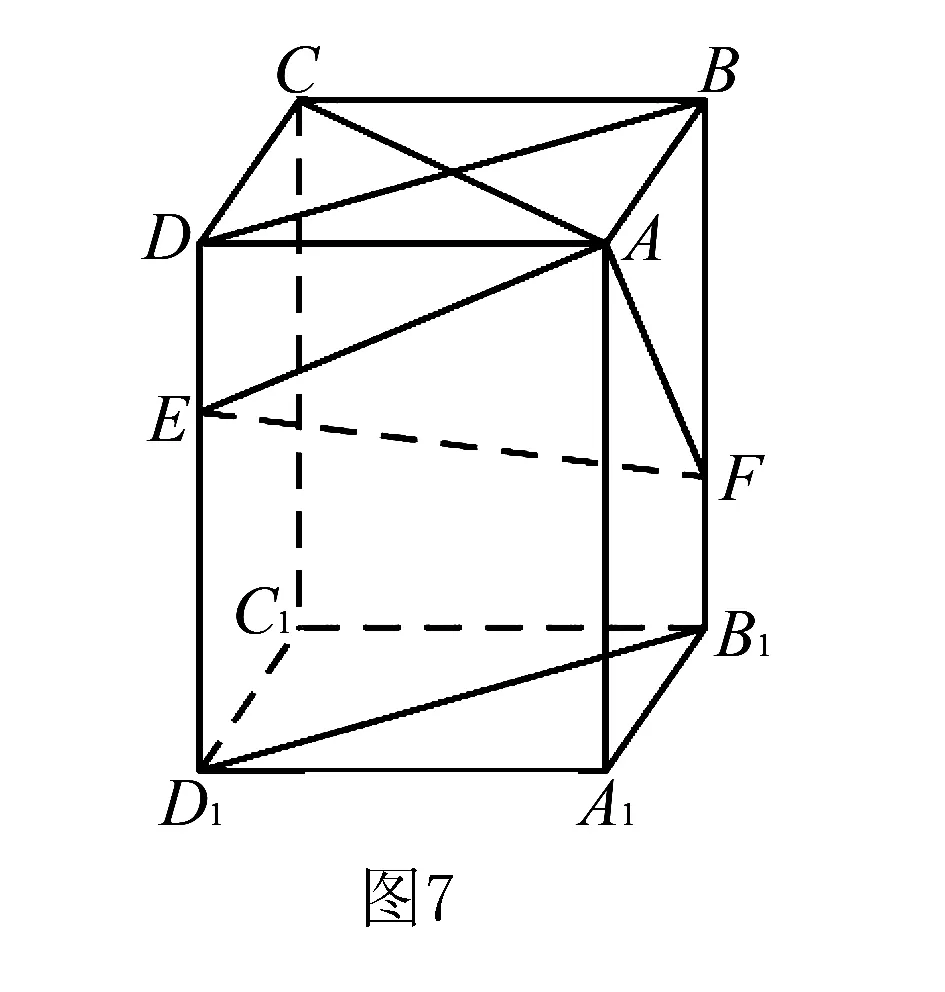
证明如图7,连接BD,B1D1.因为AB=BC,所以四边形ABCD为正方形,故AC⊥BD.又因为BB1⊥平面ABCD,于是AC⊥BB1.所以AC⊥平面BB1D1D.
由于EF⊂平面BB1D1D,所以EF⊥AC.
四、面面垂直
一个平面过另一个平面的垂线,则这两个平面垂直.


证明:平面AMD⊥平面BMC.

证明由题设知,平面CMD⊥平面ABCD,交线为CD.
因为BC⊥CD,BC⊂平面ABCD,所以BC⊥平面CMD,故BC⊥DM.

又BC∩CM=C,所以DM⊥平面BMC.
而DM⊂平面AMD,故平面AMD⊥平面BMC.
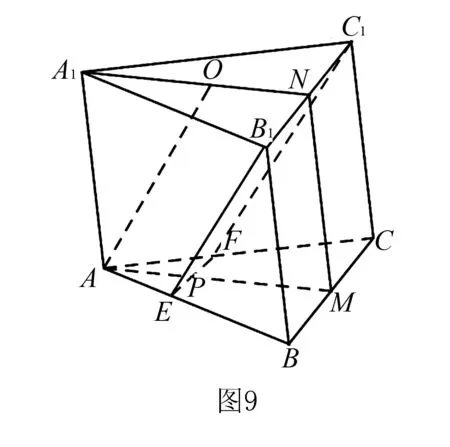
例6(2020年全国Ⅱ卷文数)如图9,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点.过B1C1和P的平面交AB于点E,交AC于点F.
证明:AA1∥MN,且平面AA1MN⊥平面EB1C1F.
分析先将需要证明垂直的两个平面用不同颜色勾勒出来,再去看题目中的条件,很快能够发现B1C1的垂直最多,所以B1C1是主线.
证明因为M,N分别为BC,B1C1的中点,
所以MN∥CC1.
又由已知得AA1∥CC1,故AA1∥MN.
因为△A1B1C1是正三角形,所以B1C1⊥A1N.
又B1C1⊥MN,故B1C1⊥平面AA1MN.
又因为B1C1⊂平面EB1C1F,
所以平面AA1MN⊥平面EB1C1F.
例7(2017年全国Ⅰ卷文数)如图10,在四棱锥P-ABCD中,AB//CD,且∠BAP=∠CDP=90°.
证明:平面PAB⊥平面PAD.
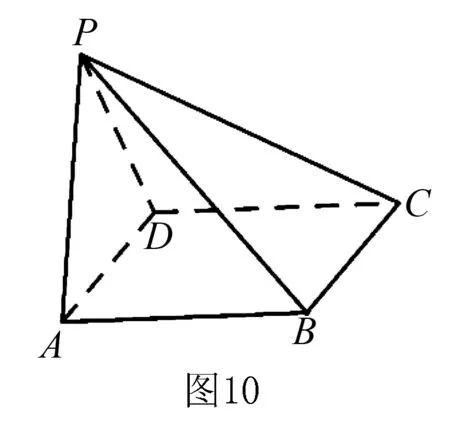
分析先将需要证明垂直的两个平面用不同颜色勾勒出来,我们发现有一条线是公共的,那么这条线一定不会是主线,剩下4条线有明显垂直的就是AB,所以AB是主线.
证明由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD.
从而AB⊥平面PAD.
又AB⊂平面PAB,所以平面PAB⊥平面PAD.
通过以上例题我们不难看出,立体几何中的垂直证明关键在于找到那条“主线”,而主线的寻找往往依赖于题目中的条件,主线一般会在垂直多的地方,大部分在底面、侧面里,很少是体的对角线(看上去是悬空的线),证明面面垂直时,两个面的公共线不会是主线,所以找出题目中的信息很关键,哪里有垂直,哪里的垂直多,整个题目的条件偏向于哪里,哪里就是这道题的“重心”,我们只需要依着这样的规律,就能够快速地破解这类题,做题时思路就会很清晰,也就能够起到事半功倍的效果!
