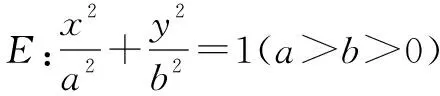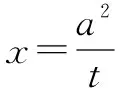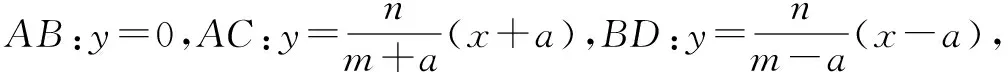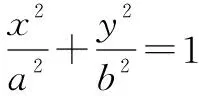对2020年高考新课标全国Ⅰ卷理科第20题的探究

李 宁 贺航飞

(海南省海南中学 571158)

一、真题再现

(1)求E的方程；

(2)证明：直线CD过定点.

二、解法探究

①

整理，得x1y2+3y2-3x2y1+9y1=0.

②

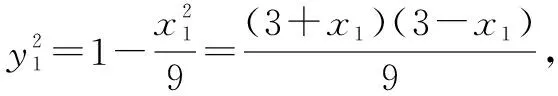
整理,得x2y1+3y1-3x1y2+9y2=0.

③

②-③，得0=6(y2-y1)+4(x2y1-x1y2).

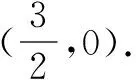
解法2 直线CD不与y轴垂直，设其方程为x=my+t，代入x2+9y2=9，

整理，得(m2+9)y2+2mty+t2-9=0.

设C(x1,y1),D(x2,y2)，则

将韦达定理的内容代入上式，得

评注这里y1和y2是不对称的，不能借助韦达定理直接消去y1,y2. 通过适当变形，消去y1，保留y2. 最后看似消元无望，提取公因式后“豁然开朗”，能够整体消元.

整理，得(9+n2)x2+6n2x+9n2-81=0.

因为-3与x1是以上二次方程的两根，

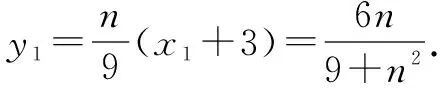
整理，得(1+n2)x2-6n2x+9n2-9=0.

因为3与x2是以上二次方程的两根，

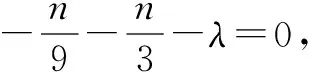
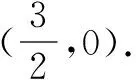
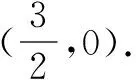
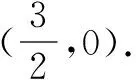
评注这里借助曲线系方程，计算量比前面的解法要小得多. 在解题时，可以将曲线系方程中的各项系数都写出来，然后和椭圆方程对照得到若干关于各个参数的方程，选取对解题有利的方程来化简.

三、问题推广

该考题的第(2)问的背景为圆锥曲线的极点、极线理论，下面将问题推广到一般情形.