大比例尺土壤保持服务制图分级方法研究
2021-04-08张丹红王效科黄斌斌
张丹红,王效科,*,张 路,黄斌斌
1 中国科学院生态环境研究中心,城市与区域生态国家重点实验室, 北京 100085 2 中国科学院大学, 北京 100049
保护和提升生态系统服务是构建生态安全保障体系的重要内容。随着生态系统服务评估方法的深入,开源生态系统服务空间数据不断增加,对区域生态系统保护规划发挥了积极作用(http://www.ecosystem.csdb.cn)。生态保护规划决策不仅要考虑生态保护指标的空间分布,也要为社会经济发展预留一定空间,以此防止生态保护与经济发展冲突加剧,通常采取生态要素空间模拟和专家决策相结合的方法进行生态保护规划和决策。因此,如何科学、直观地呈现生态服务的空间重要性分布将对决策起到至关重要的作用。通过生态系统服务数据空间分布特征可视化直观展示,决策者可直接判读生态系统服务高值区和低值区及其空间位置,确保生态服务价值最高的区域可以被纳入保护范围。但由于受到地貌、气候、土壤、植被、区位和人类活动多种因素影响,生态系统服务空间分布比较破碎。Rebecka曾报道,66%生态系统服务制图单元是基于0.01 km2或更小的粒度[1],如何既能够反映大范围生态系统服务趋势和规律,又保证具有很高的制图精度,充分显示各区域服务强度值的差异,这是生态系统服务制图综合过程中面临的最大挑战。
生态系统服务空间模拟结果通常是由各栅格中的连续数值表示的,难以直接用于空间保护规划,通过科学的制图分级将栅格数据综合成不同的级别,每一级分别用特定颜色展示,有助于实现空间数据可视化和信息获取的简化[2- 4],反映出原有数据的关键分布信息,有效支持规划决策。目前生态系统服务分布图编制时,主要采用的分级方法有自然断点法[5- 8],分位数法[9]和累积比例法[10-11]等,但在如何选择分级方法以及分级效果对比方面仍有不足。
分级方法是获取数据分布信息和决定制图质量的关键因素[12]。缺少科学依据的生态服务分级方法极大限制了生态服务要素在区域生态保护规划中的应用。为此,国内外学者对分级方法质量评价进行了大量研究。从Jenks[13]早期提出级内误差最小化来测量分级精度,分级方法质量评价逐渐朝多指标评价方向发展。目前常用的分级方法质量评价指标包括数理统计指标和空间指标。数理统计指标如分级精度[13-17]、信息熵[18-19]和相对信息熵Hrel[20]等。空间指标如地理面积不均等程度指标[21-22]、空间自相关性指标[21- 24]等。但不同分级方法下,综合统计指标和空间指标的多指标分级效果评价研究较少,目前分级质量评价中所用指标不统一,指标各有优劣。如分级质量评价中分级精度指标众多,党安荣分析了不同分级精度模型后认为陆效忠[16]提出的分级精度指标体系所考虑的因素及公式参数最完善[25],可以对分级精度进行更精确的评价。本文选取陆效忠4种分级精度指标中参数最完善的相对平均偏差分级精度指标,该指标排除了分级后各级数量累积误差和值域范围较大对误差计算的影响,更适用于数据量较大,值域范围较大的土壤保持服务强度数据分级精度评价。Armstrong 等采用了空间自相关系数指标评价分级方法[22,24]的空间自相关性,计算分级后的空间自相关性Morans′I,认为Morans′I越大,则分级效果越好。但郭庆胜提出分级后的 Morans′I不一定越大越好,而应该与原始数据的空间自相关性保持一致[22],但未提出衡量空间自相关一致性的方法,所以,本研究建立空间自相关一致性指标评价分级方法反映原始数据的空间自相关性的程度。本研究对众多的分级评价指标进行筛选、综合和改进后构建适合土壤保持服务强度数据特征的分级效果评价指标,以我国6个典型县区的土壤保持服务强度数据库为基础,采用5种分级方法编制1:25万服务分布图,根据各分级方法分级质量的比较研究,建立了生态系统服务制图分级方法的优选方法,以期为大比例尺相关生态系统服务制图提供选择分级方法的理论依据和方法。
1 研究方法
1.1 研究区域与数据来源
本研究采用土壤保持强度(t hm-2a-1)数据表示土壤保持服务功能,由修正的通用土壤流失方程[17]计算,时间为2015年,空间分辨率为90m。为体现全国土壤保持强度的空间分布差异,选取中国不同区位的6个县区为研究区。分别为北京市延庆区(面积约1994 km2,土壤保持强度值域为0—1246 t hm-2a-1)、吉林市的丰满区(面积约为10601 km2,土壤保持强度值域为0—1872 t hm-2a-1)、云南省县级市安宁市(面积约为1301 km2,土壤保持强度值域为0—2522 t hm-2a-1)、杭州市辖区富阳区(面积约为1821 km2,土壤保持强度值域为0—4744 t hm-2a-1)、隶属甘肃省临夏回族自治州的永靖县(面积约为1864 km2,土壤保持强度值域为0—1578 t hm-2a-1)、隶属乌鲁木齐市的天山区(面积约为245 km2,土壤保持强度值域为0—118 t hm-2a-1)。
1.2 制图分级方法
本研究选择等差分级法、自然断点法、几何间隔法、分位数法和累积比例法等5种分级方法对土壤保持强度进行分级,5种分级方法原理见表1,结合制图尺度、分级科学性和可读性,分级数设置为5级。
1.3 分级目标及定量指标
根据制图分级理论,分级应满足分级精度和信息量要求,结合土壤保持强度数据特征,构建的制图分级目标和定量指标如表2所示:
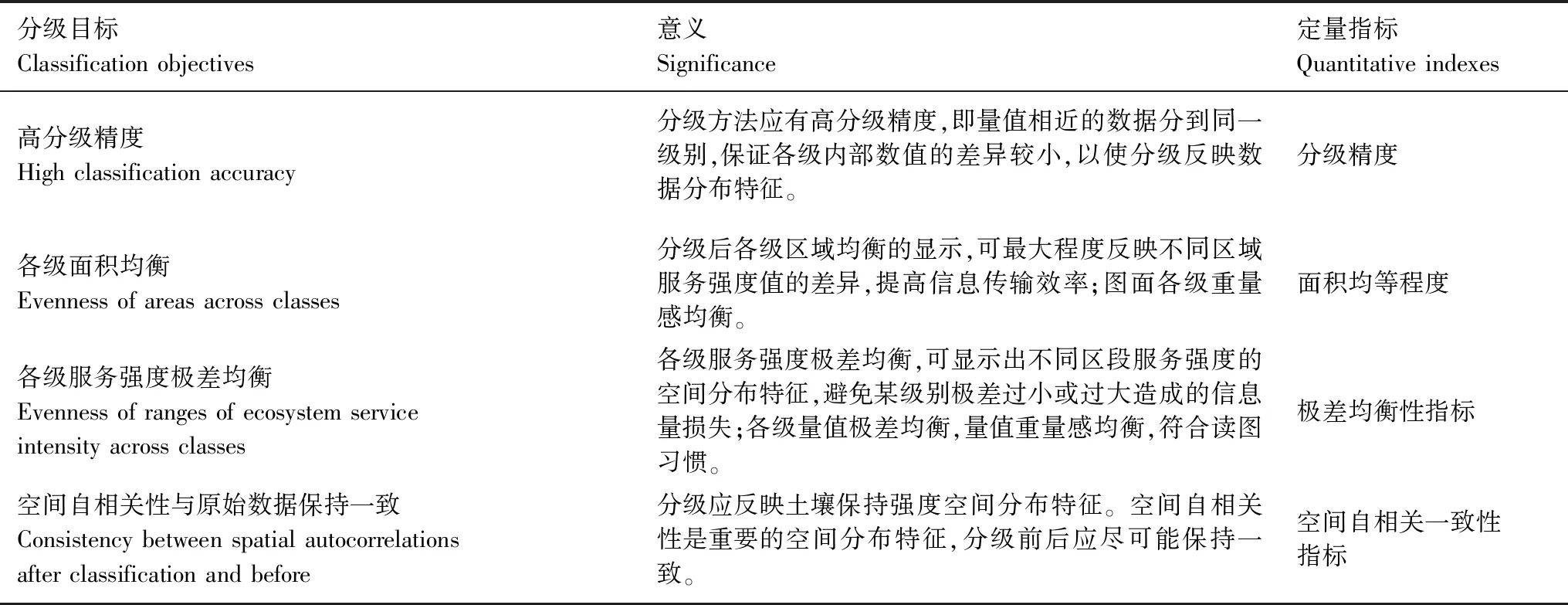
表2 分级目标及定量指标
1.4 分级方法评价指标
(1)分级精度AC(Accuracy of classification)
AC用平均相对偏差表示,即各级内平均相对变异之和与平均总相对变异之比。AC指标值越大,则分级误差越小,分级精度越高[16]。公式如下:
(1)
(2)面积均等程度(Areal equality)
AE指标描述分级面积均等程度,基于信息熵理论和制图视觉重量感,分级后各级面积越相等,分级质量越好。制图信息理论认为,分级后各级面积越均等,确定一个栅格级别归属的不肯定程度越大,所需要的信息量越大[19- 20],分级效果越好,常用相对信息熵Hrel[20]比较当分级数确定情况下,各分级方法的分级信息量大小,即分级面积不均衡程度。同时,各级面积越均等,各级视觉重量感越均衡,分级效果越好[14,21-22],常用GEA[21-22]描述各级面积的不均衡性,将其变形后得GEAS描述各级面积的均等程度。将Hrel和GEAS组合构建AE,公式如下:
(2)
(3)
(4)
式中,k为分级数,P为各级内部栅格数与总数栅格数比值。i为各级序号。Aj、A别为第j级和总栅格数,A1,……,Ak按升序排列。Hrel、GEAS分别为相对信息熵[20]和面积均等程度,取值范围在0和1之间,分级后,各级面积越均等越接近1。
(3)极差均衡性指标EVR(Equality of value ranges of classes)
该指标描述分级后各级服务强度极差的均等程度。对于数值连续且分布不均衡的土壤保持强度数据,追求分级面积均衡可能导致各级服务强度极差差异较大。而分级后各级的服务强度极差重量感均衡,符合读图者的习惯。且从信息量角度,量值几乎相近的栅格数据划分为不同的级别造成级别信息冗余,而同一级别服务强度值范围很大则量值信息过度综合,造成信息量损失。因此,本文通过基于视觉重量感的不均等程度指标GEA[21-22]和基于信息论的相对信息熵指标Hrel变形为视觉重量感均衡程度指标GEASIE和HrelIE组合构建极差均衡性指标EVR,将各级服务强度极差带入公式计算极差的均衡性。公式如下:
(5)
(6)
(7)
式中,EVR指标阈值在0和1之间, 各级服务强度极差越均等指标值越大。k为分级数,ρj、σ分别为第j级和服务总极差。i为各级的序号。Pi为i级极差与总极差的比值。
(4)空间自相关一致性指标SACC(Spatial autocorrelation consistency)
该指标描述分级后空间自相关格局与原始数据空间自相关性格局的接近程度。公式如下:
(8)
(9)
(10)
(11)
式中,q为分级方法代号,Morans′I理论范围为[-1,1],Morans′Iraw为原始数据的空间自相关性,Morans′Iq为分级后级别土壤保持强度平均值代替该级别栅格数值计算的空间自相关性。zi是栅格i的数值与总体均值的偏差,wi,j为空间权重。Morans′I指数由ArcGIS 10.5 Spatial Autocorrelation(Morans′I)工具计算,权重为默认值,原理如公式(9)—(11)。
根据分级原则,综合分级质量评价需满足分级精度最大化、各级面积均衡、各级服务强度极差均衡及空间自相关特征不变等要求。为了排除各指标敏感性对综合评价值的影响,将各指标中心化、标准化后计算综合评价值。公式如下:
(12)
(13)
(14)
式中,n为指标个数,本研究n=4。I,i分别为指标评价值和代号,CIi、SCIi分别为中心化及中心化并标准化后的指标评价值,SCIi为负值表示所有分级方法中该分级方法的i指标评价值处于平均水平以下。分级方法的综合评价值用IAV(Integrated assessment value)表示,表示为该种分级方法中心化并标准化后的各指标之和。
本研究使用ArcGIS 10.5相应分级模块实现6个县市土壤保持强度数据集4种分级方法(几何间隔法、自然断点法、等差法及分位数法)的分级;使用EXCEL表格和ArcGIS 10.5实现6个县市土壤保持强度数据集累积比例法分级:用ArcGIS 10.5导出各县市的服务强度及频数的属性表,用EXCEL打开,按服务强度的从大到小顺序排序,将各栅格服务强度累加,计算累加值占总值的比例,找出累积比例25%,50%,75%,90%对应的分级界限,在ArcGIS 10.5的分级模块中手动输入相应的分级界限值,实现各县区土壤保持强度累积比例法分级;用R语言计算各县区不同分级方法的评价结果:首先,用R语言读取各县区的土壤保持强度及频数的属性表,输入各分级方法分级界限值,通过编程好的R语言代码计算各分级方法的评价结果;用Excel软件对分级评价结果进行可视化制图。
2 结果分析
2.1 分级方法各级服务强度和面积占比比较
分级结果显示(图1),同一分级方法各级服务强度极差和各级面积占比在6个县区中有一定程度的相似特征。通过6个县区各级的服务强度极差占比的直观比较,等差法各级占比最均衡,各级约为20%;自然断点法次之,各级服务强度值极差占比范围为4.2%—51.7%;累积比例法各级变异相对较大,各级服务强度值极差占比范围为3.4%—78.8%;分位数法和几何间隔法变异最大,各级服务强度极差占比范围分别为0.59%—90.6%和0.39%—84.7%,第1级别服务强度的极差占比最小,分别仅占最大值的0.59%—4.1%和0.39%—3.9%。
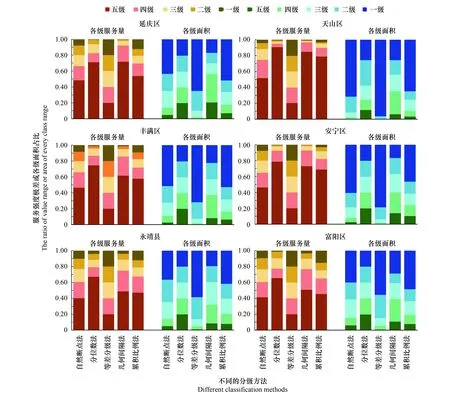
图1 6个县区各分级方法得到的各级土壤保持强度极差和面积占比Fig.1 Distribution of range ratio of soil retention service intensity and area ratio of every class using different classification methods in 6 counties
对于各级的面积占比的直观比较,大多数县区,分位数法各级面积最均衡。几何间隔法次之,各级面积占比范围为6.2%—28.8%;累积比例法各级面积占比变化相对较小,范围为3.1%—64.9%;自然断点法在多数县区各级面积占比变化较大,范围为0.29%—71.7%,从低级到高级递减,第5级别面积占比范围为0.29%—6.0%,都小于累积比例法第5级别面积占比,其中,天山区占比最小,仅为0.29%,其他县区大于2.5%;等差法各级面积分布变异最大,各级面积占比变化范围为0.003%—96.4%,低级到高级面积占比减少,第5级占比很小,范围为0.003%—0.8%,而第1级面积占比很大,范围为55.6%—94.6%,其中,天山区和安宁市第1级分别占了96%和80%的面积。
2.2 不同分级方法的各指标评价结果比较
通过中心化和标准化处理后,5种分级方法各指标评价值的均值为0(图2)。分级精度评价结果显示,6个县区等差法的AC值最高,范围为0.89—1.37,这说明等差分级法在5种分级方法种分级精度最好;累积比例法AC值大于均值,范围为0.25—0.81,自然断点法AC值接近或大于均值,范围为-0.01—0.75,除安宁市,其他县市AC值均低于累积比例法,这说明累积比例法和自然断点法分级精度较优,对于多数县区累积比例法分级精度优于自然断点法;几何间隔法和分位数法AC值明显低于均值,范围分别为-1.14— -0.64和-1.42— -0.81,这说明几何间隔法和分位数法相对于其他分级方法分级精度明显较差。
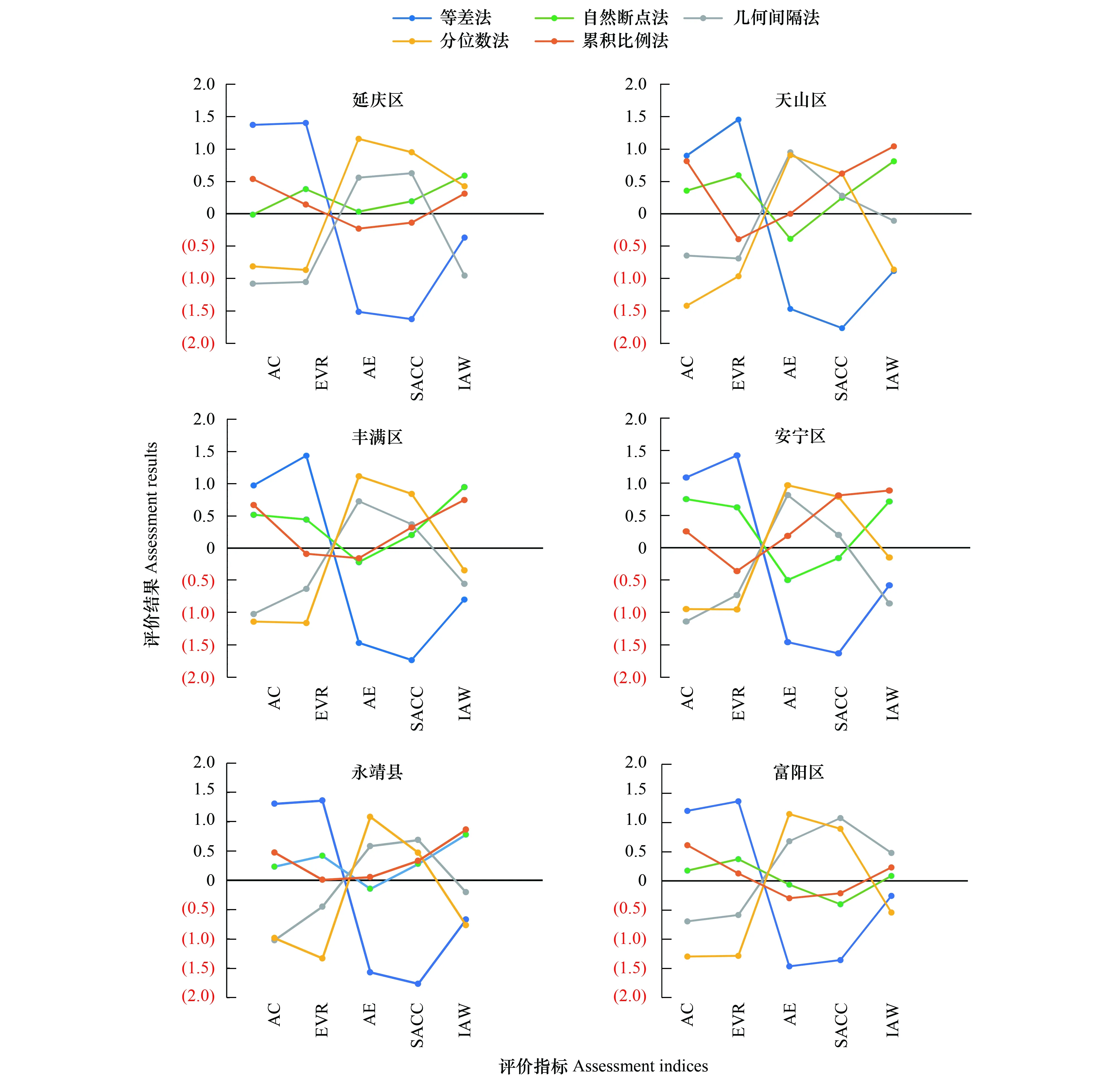
图2 6个县区分级方法评价结果Fig.2 Evaluation results of classification methods of soil retention services of 6 countiesAC, 分级精度 Accuracy of classification methods; EVR, 极差均衡性指标Equality of value ranges of classes; AE, 各级面积均衡性 Areal equality; SACC, 空间自相关一致性 Spatial autocorrelation consistency; IAV, AC、AE 、EVR、SACC的综合评价值 Integrated assessment value
极差均衡性评价结果显示(图2),6个县区等差法各级服务强度极差最均衡,EVR值高于其他分级方法,范围为1.36—1.45;自然断点法次之,范围为0.37—0.62,大于均值,说明自然断点法各级服务强度极差较均衡;累积比例法接近均值,为-0.39—0.14,说明累积比例法各级服务强度极差均衡性一般;几何间隔法和分位数法EVR值明显小于均值,分别为-1.06— -0.45 和-1.33— -0.87,除延庆区,分位数法EVR值都低于几何间隔法,说明几何间隔法和分位数法各级服务强度极差不均衡,对于大多数县市,分位数法不均衡程度更高。
面积均衡性评价结果显示,分位数法AE值范围为0.90—1.12,几何间隔法AE为0.55—0.95,除天山区几何间隔法AE值接近于分位数法,其他县市都低于分位数法,说明对于大多数县区分位数法分级面积最均衡,几何间隔法次之;累积比例法和自然断点法的AE值接近于均值,分别为-0.30—0.18和-0.50—0.03,面积均衡性一般;等差法AE值-1.57—-1.46,明显低于均值,体现出等差法分级各级面积十分不均衡。
空间自相关一致性评价结果显示,分位数法和几何间隔法SACC值范围分别为0.47—0.95,和0.20—1.08,明显大于均值,除永靖县和富阳区外,其他县区分位数法SACC值大于几何间隔法,说明对于大多数县区分位数法分级与原数据的空间自相关格局最接近,几何间隔法次之;累积比例法SACC值范围-0.21—0.80,大于或接近于均值,说明累积比例法分级可反映原数据的空间自相关格局;自然断点法SACC均接近于均值,范围为-0.40—0.27,与原数据的空间自相关接近程度一般;等差法SACC值为-1.76— -1.36,明显低于均值,说明等差分级法分级对原数据空间自相关格局改变较大。
2.3 各分级方法综合评价结果比较
由图2进一步分析,对于各县区不同分级方法的综合评价值,水平轴代表5种分级方法综合评级值的均值。6个县区中,延庆区自然断点法IAV值最高,为0.60,分位数法次之,IAV值为0.42,累积比例法IAV值为0.31,与分位数法接近,而等差分级法和几何间隔法IAV值小于均值,说明延庆区自然断点法综合制图效果最优,分位数法和累积比例法综合制图效果较优,而等差法和几何间隔法综合制图效果较差;天山区累积比例法IAV值最高,为1.34,自然断点法次之,为0.81,几何间隔法、分位数法、等差法低于均值,分别为-0.11,-0.86和-0.88,说明天山区累积比例法综合制图效果最好,自然断点法综合制图效果较优, 几何间隔法综合制图效果较差,而分位数法和等差分级法综合制图效果最差;对于丰满区,自然断点法IAV值最高,为0.95,累积比例法次之,为0.75,分位数法、几何间隔法和等差分级法IAV值均小于均值,分别为-0.34,-0.55和-0.80,对于丰满区自然断点法综合制图效果最优,累积比例法综合制图效果较优,分位数法、几何间隔法、等差法综合分级质量较差;对于安宁市,累积比例法IAV值最高,为0.88,综合制图效果最优,自然断点法IAV值为0.71,综合制图效果较优,其他分级方法IAV值都小于均值,综合制图效果较差;对于永靖县,累积比例法和自然断点法IAV值分别为0.86和0.78,两者接近,说明累积比例法和自然断点法综合制图效果都较好,累积比例法略优于自然断点法,其他分级法IAV值小于均值,综合制图效果较差;富阳区几何间隔法IAV值最高,为0.48,累积比例法和自然断点法IAV值分别为0.23和0.08,等差分级法和分位数法IAV值小于均值,说明富阳区几何间隔法综合制图效果最优,累积比例法和自然断点法综合制图效果较好,累积比例法略优于自然断点法,等差分级法和分位数分级法综合制图效果较差。
3 结论与讨论
3.1 讨论
从分级方法各级服务强度极差和面积占比分布来看(图1),等差法能够直观的反映出6个县区土壤保持服务分布有相似的特征,即空间分布不均衡,低值区所占面积较大,低于最大服务强度20%的强度值占了大于50%的面积,高值区所占面积较小,高于最大服务强度80%的强度值覆盖面积小于0.8%,6个县区中天山区分布最不均衡,安宁区次之。
由于各县区相似的土壤保持服务分布特征,每种分级方法的各指标和综合评价结果在6个县市显示出相似的特征。在5种分级方法中,累积比例法和自然断点法综合评价值都较高,且各指标评价结果较优,综合制图效果较好;分位数法和几何间隔法分级后各级面积分布较均衡,分级后的空间自相关性与原始数据较一致,说明图面各级呈现聚集分布特征,清晰可辨,但两种分级方法分级精度较低,极差不均衡,这影响了大多数县区的综合制图效果;等差分级法虽然有较高的分级精度,各级服务强度极差分布均衡,但各级面积不均衡,低级区占据了较大的图面面积,高级区所占面积极小,几乎不能辨识,分级也不能反映原有数据的空间自相关分布格局,综合制图效果较差,不适合空间分布不均衡的土壤保持强度数据集的分级。
不同县市的土壤保持服务分布也有差异性,每种分级方法的各指标和综合评价结果也有一定程度的变化。几何间隔法和分位数法综合评价值在6个县区中的波动较大,延庆区分位数法综合分级效果接近于最优,富阳区几何间隔法综合分级效果最优,在这两个县市分位数法或几何间隔法分级后的面积均衡性和空间自相关一致性较其他分级方法有明显的优势,分级精度和各级服务强度极差一致性评价值虽然较低,但对综合制图效果未造成较大影响,其他县区两种分级方法综合评价值较差,尤其是服务强度分布不均衡的天山区,分位数法各级极差分别为1,2,3,5,107 t hm-2a-1,几何间隔法各级极差分别为1,1,2,14,100 t hm-2a-1,可见两种分级方法低级区极差间隔极小,几乎没有差别的服务强度值划分到不同的等级,而高级区服务强度变化范围较大,却用相同的级别表示,图面整体服务强度信息损失较大,同时分级图较大程度偏离了原有数据分布特征;自然断点法在土壤保持强度数据集不均衡程度较大的天山区和安宁市,分级后各级面积不均衡程度也较大,最高级区面积较小,制图呈现出较破碎化的特征;累积比例法在6个县区综合评价值始终为最优或接近于最优,结合图1,累积比例法各级面积和各级服务强度极差占比没有过小的情况,最高级面积占比均大于自然断点法,说明分级图高级区聚集程度高于自然断点法,破碎化程度相对较小。可见,在5种分级方法中累积比例法适用性最广,能较好的适用于6个县市土壤保持强度数据集的分级。
本研究的多指标综合评价结果能够较可靠的反映出不同分级方法的相对优劣,有助于筛选出不同数据集对应的最优分级方法。对于综合评价值接近的分级方法,由于各指标分级质量的优劣不同,综合制图效果也有差异,可进一步综合分级结果(图1)和各指标评价结果(图2)筛选出理想的分级方法:若注重分级后各级的聚集程度和面积均衡,则考虑几何间隔法和分位数法,若注重更高的分级精度和各级服务强度极差均衡,则考虑自然断点法和累积比例法,同时追求最高级破碎程度小、易于辨识,则累积比例法优于自然断点法。
从各分级方法评价结果发现,在6个县区中累积比例法综合评价值最优或者接近最优,相较于其他分级方法适用性最广,在各县区都呈现理想的制图效果。这说明本研究设置的累积比例较适用于各县市土壤保持强度数据集分级。累积比例法分级,在反映出土壤保持强度分布特征的同时,各级累积量相对固定,可比性较强,较适合于多县区的比较制图。
进一步用累积比例法对各县区土壤保持强度进行分级制图(图3),图面效果显示,6个县区累积比例法所分各级都能清晰显示在图面上,各级代表的服务强度也有明显的差异,分级图信息量丰富,较符合实际的刻画出土壤保持服务的空间分布特征,综合制图效果较好。
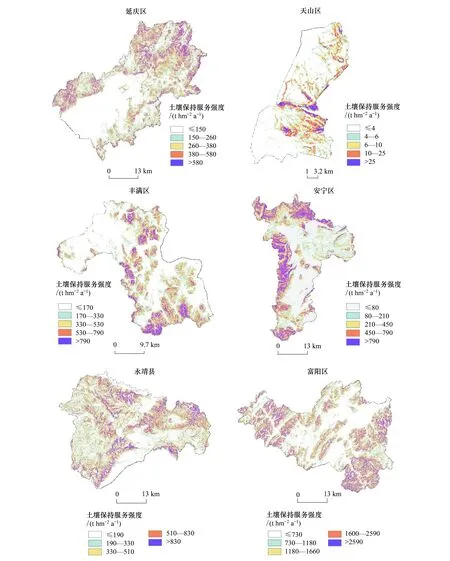
图3 6个县土壤保持强度分级制图Fig.3 Mapping intensity of soil retention services in 6 counties using excellent classification methods
由于受到5种备选分级方法的限制,评价结果筛选出的分级方法不是绝对最优, WebGIS[26-28]等网络制图和参与式[29]制图的发展,在本研究的理论方法基础上开发交互式分级评价工具[30],嵌入到制图软件中[18,31],可方便制图者参考分级评价结果改动分级界限,进一步评价择优,不断探索更优的分级方案。同时,随着计算机计算能力不断提高,算法研究不断进步,将评价指标写入算法通过不断迭代,计算出最优分级界限逐渐成为可能[21],这将是今后进一步研究的方向。
3.2 结论
结合制图学理论,根据土壤保持服务数据统计分布特征和空间分布特征,除了考虑分级精度,各级面积均衡程度,还设置了极差均衡性、空间自相关一致性指标,对土壤保持服务数据常用的5种分级方法做评价分析,得出以下结论:
(1)对于分布在我国不同地方的6个县区,土壤保持服务分布差异较大,但呈现相似的分布特征,即空间分布不均衡,高值区面积较小,低值区面积较大,低于最大服务强度20%的强度值占了大于50%的区域面积。
(2)本文选择的4个制图效果评价指标,从不同侧面反映了生态系统服务的空间分布规律和制图工作要求,综合评价结果能反映出各县区不同分级方法综合分级质量的优劣程度。
(3)综合评价结果显示,不同县市的最优分级方法有差异,其中,延庆区、丰满区最优分级方法为自然断点法,永靖县、天山区、安宁市最优分级方法为累积比例法,富阳区最优分级方法为几何间隔法。累积比例法综合制图效果在6个县市最优或接近于最优,且各指标评价值较优,对不同数据集的适用性最好。
(4)本研究提供的分级方法质量评价的理论和方法,可为大比例尺生态系统服务栅格数据制图工作者提供科学选择分级方法的参考,提高制图的效率,也可作为自动化选择分级方法的参考。
致谢:饶恩明老师提供部分测量数据,特此致谢。
