气体性质类计算题的解题策略

山东 张岩松 韩在峰

2016年之前，山东物理高考题采用的是山东卷。2016年-2019年山东物理高考题采用的是课标全国卷Ⅰ，试题形式是理综卷。选修3-3热学部分属于选修知识，考两道题，第一道题是选择题，分值是5分；第二道题是计算题，分值是10分，这道计算题每年均考查气体的性质。以玻璃管液柱模型和气缸活塞模型为主。

从2020年开始，山东省高考物理题再次回归使用山东卷，原选修3-3中的热学知识、选修3-4中机械波和光学知识以及选修3-5中原子、原子核知识都变成了必考知识。而且山东高考题每年的第15题(7分)，考查内容均为选修3-3中气体的性质或考查选修3-4中机械波和光学知识，为固定的二选一情况。今年考查了气体的性质，背景为中医拔罐，实际上属于“玻璃管液柱”模型，“罐”相当于玻璃管，“皮肤”相当于液柱。下面以近几年的高考题为例，具体对此类问题进行分析和解答，并总结、归纳出常用的解题方法和策略。

一、玻璃管液柱模型

【例1】[2020年全国卷Ⅲ第33题(2)]

(2)(10分)如图1所示，两侧粗细均匀、横截面积相等、高度均为H=18 cm的U型管，左管上端封闭，右管上端开口。右管中有高h0=4 cm的水银柱，水银柱上表面离管口的距离l=12 cm。管底水平段的体积可忽略。环境温度为T1=283 K。大气压强p0=76 cm Hg。

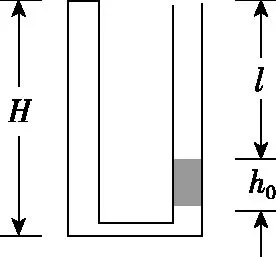
图1

(ⅰ)现从右侧端口缓慢注入水银(与原水银柱之间无气隙)，恰好使水银柱下端到达右管底部。此时水银柱的高度为多少？

(ⅱ)再将左管中密封气体缓慢加热，使水银柱上表面恰与右管口平齐，此时密封气体的温度为多少？

【解析】(ⅰ)设玻璃管的截面积均为S，以封闭的气体为研究对象。

令开始的平衡状态为状态1，设右管水银柱下方的气体长度为h1。

由图2可以看出h1=H-l-h0=2 cm

故V1=(H+h1)S=(18+2)S=20S

p1=p0+h0=76+4=80 cm Hg

令水银柱下端恰好到达右管底部时为平衡状态2，设此时水银柱的高度为h。

则V2=HS=18S

p2=p0+h=76+hcm Hg

因为T2=T1=283 K，根据玻意耳定律可知

p1V1=p2V2

故80×20S=(76+h)×18S

解得h=12.9 cm

故此时水银柱的高度为12.9 cm。

(ⅱ)令水银柱上表面恰与右管口平齐时为平衡状态3，设此时气体的温度为T3。

此时的体积V3=(2H-h)S=23.1S。

由平衡状态2到平衡状态3，经历的是等压过程。而

T2=T1=283 K

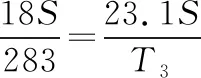
解得T3=363 K。

说明：也可以利用状态1和状态3，根据理想气体的状态方程列式求解。

【小结】玻璃管液柱模型的解题策略：

玻璃管液柱模型是考查气体性质试题中常遇到的题型，玻璃管形状无论是直管还是U型管，还是其他形状的玻璃管，玻璃管放置无论是水平放置、竖直放置，还是其他角度放置，玻璃管无论是固定，还是存在着转动的情况、涉及的气体无论是一段气体还是两段气体，解题思路都是相同的，可以说是万变不离其宗，都是先选取某段气体为研究对象，然后再设法求解在各个平衡状态之下的三个状态参量，最后利用气态方程或者气体实验三定律列方程求解。其中气体的三个状态参量中求压强是关键，而压强的计算往往涉及研究对象的选取和受力分析，此部分常与力学知识相结合。因此将热学问题力学化是解决此类问题的突破口和切入点。

另外，在求解各个平衡状态下的体积和压强时，有时画出草图，会快速寻找到各个平衡状态下气体体积和压强关联。再者，有时还要特别注意抓关键词、临界状态、水银是否流出等。

二、气缸活塞模型

【例2】[2018年全国卷Ⅱ第33题(2)]

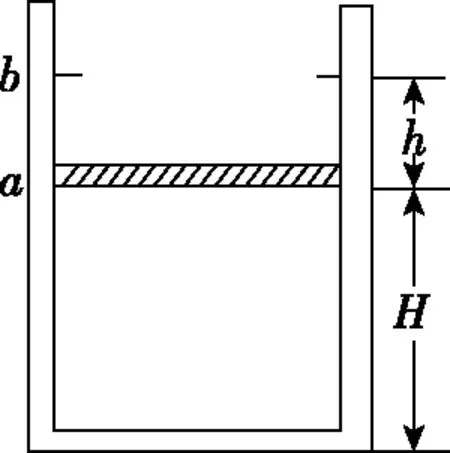
图2

(2)(10分)如图2所示，一竖直放置的气缸上端开口，气缸壁内有卡口a和b，a、b间距为h，a距缸底的高度为H；活塞只能在a、b间移动，其下方密封有一定质量的理想气体。已知活塞质量为m，面积为S，厚度可忽略；活塞和汽缸壁均绝热，不计他们之间的摩擦。开始时活塞处于静止状态，上、下方气体压强均为p0，温度均为T0。现用电热丝缓慢加热气缸中的气体，直至活塞刚好到达b处。求此时气缸内气体的温度以及在此过程中气体对外所做的功。重力加速度大小为g。

【试题分析】(1)由于活塞处于平衡状态，所以可以利用此平衡状态，列平衡方程，求封闭气体的压强。这是将热学问题力学化。

(2)本题的关键是找到不同状态下的气体状态参量，再利用气体实验三定律求解。

(3)通过关键词，挖掘隐含条件：

①“缓慢加热”表示活塞始终处于平衡状态；

②活塞在卡口1处刚要开始运动时，此时，活塞与卡口之间无相互作用力；

③“活塞刚好到达b处”说明活塞与b卡口处无弹力作用。

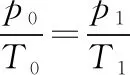
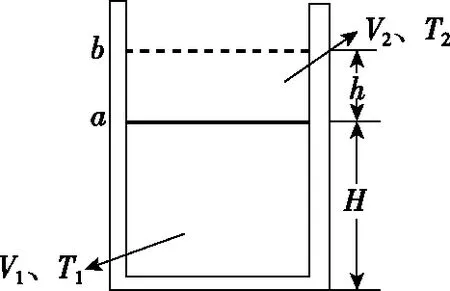
图3

因为活塞刚要开始运动，因此活塞与卡口之间无相互作用力，根据力的平衡条件有p1S=p0S+mg

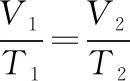
式中V1=SH

V2=S(H+h)

从开始加热到活塞到达b处的过程中，气缸中的气体对外做的功为W=(p0S+mg)h

故W=(p0S+mg)h

气缸活塞模型的解题策略：

气体经历了三个不同的状态，分别找出这三个状态下的各个状态参量是解题的关键。

状态1：初始状态

体积V0=SH；压强p0；温度T0

状态2：活塞在卡口a处，刚要开始运动时

体积V1=SH；压强设为p1；温度设为T1

其中选活塞为研究对象，p1可根据二力平衡求得。

从状态1到状态2，为等容变化，由查理定律可求出T1

状态3：活塞刚好到达b处

体积V2=S(H+h)；压强p2=p1；温度设为T2

从状态2到状态3，为等压变化，由盖—吕萨克定律求出T2，气缸中的气体对外做的功，由功的定义式求出。

【小结】本题属于单缸、一段气体的问题，一般的解题策略是：首先，选取研究对象，研究对象就是这段气体；然后找出各个状态下的三个状态参量；最后，根据气体实验三定律或气态方程去分别列方程求解。其中，求压强是关键，求压强需要选活塞或气缸为研究对象，根据二力平衡或者牛顿第二定律求解，将热学问题力学化。

三、练习题：2020年山东卷第15题

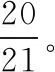
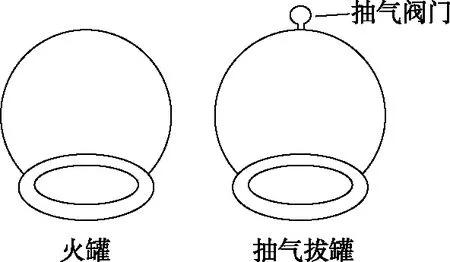
图4

【试题分析】研究对象是拔罐(玻璃罐)内的气体，涉及的拔罐过程有两个，一个是使用火罐，另一个是抽气拔罐。

涉及的气体平衡状态有三个(设大气压强为p0、玻璃罐的容积是V0)：

状态1：火罐和抽气拔罐之前的状态

p1=p0；T1=450 K；V1=V0

状态2：火罐降温至300 K时的状态

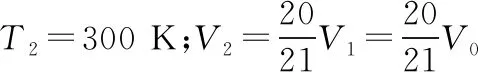
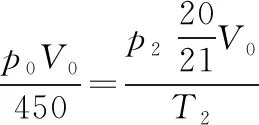
解得p2=0.7p0

状态3：抽气拔罐结束时的状态

因为抽气后罐内气压与火罐降温后的内部气压相同，所以p3=p2=0.7p0

因为忽略抽气过程中气体温度的变化，所以T3=T1=450 K。

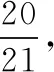
状态1和状态3联立，因为温度不变，根据玻意耳定律可知p1V1=p3V3

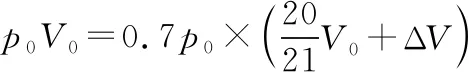
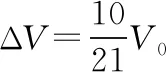
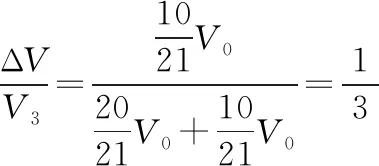
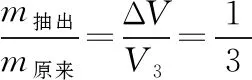
【解析策略】1.明确三个平衡状态下的三个状态参量是解题的前提。首先，利用状态1和状态2，由于三个状态参量都发生了变化，所以，需要根据理想气体的状态方程去求p2(特别注意p3=p2)。然后利用状态1和状态3，因为温度不变，所以根据玻意耳定律列方程，求出抽出的气体体积ΔV，其余问题便迎刃而解。

2.抽气拔罐的过程是个变质量问题，这是本题的难点所在。需要将变质量转化为恒质量。那么，怎样转化呢？假设被抽出的气体被一个无形的袋子装着，保持和被抽出罐内的气体温度和压强一样。这样，就把变质量的问题转化成了恒质量问题，再利用玻意耳定律求解即可。

四、对气体性质计算题解题方法的归纳和总结

1.涉及的主要知识点

理想气体的实验三定律；理想气体的状态方程；受力分析；牛顿第二定律；共点力平衡等知识。

2.解题的一般步骤

(1)明确研究对象

研究对象有两个，一个是力学研究对象，活塞或者是气缸，以活塞或者是气缸为研究对象，目的是求压强；另一个是热学研究对象，被封闭的气体，以气体为研究对象，目的是求题目所要求的未知量。

(2)分析物理过程

以活塞或者是气缸为研究对象，根据力学平衡知识，或者牛顿第二定律，求出其在各个状态下的压强，为利用气体实验定律做好铺垫。

以气体为研究对象，然后设法去寻找它在各个平衡状态下的三个状态参量，即体积、温度和压强。

(3)列方程求解

将各个状态下的三个状态参量分别带入气态方程或者是气体实验三定律，列方程求解即可。

3.解题的难点

压强的计算是难点，求压强往往会变成力学问题，涉及研究对象的选取和受力分析，因此，把“热学问题力学化”是解这类试题永恒不变的主题。也就是说，这类试题的本质是力学平衡问题。

五、高三第二轮气体性质内容复习的建议

对于山东的考生，每年的高考题第15题(7分)考气体性质计算题的概率是百分之五十；而对于全国卷的考生，每年的第33题第(2)问(10分)，无一例外的要考气体性质的计算题。这部分试题难度不大，方法也比较单一，只要经过适当的练习，并注意总结方法，得满分比较容易，它比力学题和电学题要简单得多。所以，同学们复习过程中对这部分知识一定要给予足够的重视，平时要注意玻璃管液柱类模型题和气缸活塞类模型题的训练，抓住规律，高效复习。