极值问题的分析方法及注意事项

安徽 邵 永 王法远

在《课程标准》中虽然对极值问题没有明确说明，但高考试题中却频繁出现，且难度较大，这类问题是指在物体运动的过程中，随着条件连续渐变越过临界位置时或条件连续渐变达到临界值时，会使得某物理量达到最大或最小的现象，所以这类问题与临界问题是两类问题，但往往又互为条件。在实际教学中，笔者发现学生分析此类问题时方法单一并且易混淆临界问题与极值问题，缺少必要的分析和讨论，因而失分较多。下面通过对极值问题的一题多解和数学极值与物理临界对极值问题的影响分析，突出数学知识在物理中的应用，培养学生思维的严谨性、深刻性，提高学生的理性思维能力和分析问题解决问题的能力。

一、极值问题的一题多解

【例1】如图1所示，在粗糙水平台阶上静止放置一质量m=0.5 kg的小物块，它与水平台阶表面间的动摩擦因数μ=0.5，且与台阶边缘O点的距离s=5 m。在台阶右侧固定了一个以O点为圆心的圆弧形挡板，以O点为原点建立平面直角坐标系，挡板上边缘P点的坐标为(1.6 m，0.8 m)。现用FT=5 N的水平恒力拉动小物块，一段时间后撤去拉力，小物块最终水平抛出并击中挡板(g=10 m/s2)。

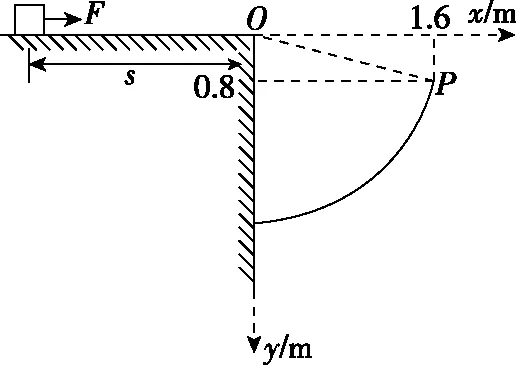
图1

(1)若小物块恰能击中挡板的上边缘P点，求拉力F作用的距离；

(2)改变拉力F作用的时间，小物块可击中挡板的不同位置，求小物块击中挡板时动能的最小值(结果可保留根式)。

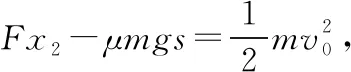
(2)解法一 不等式法

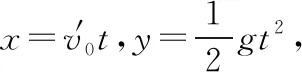
解法二 Δ判别式法

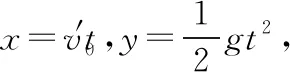
解法三 不等式法

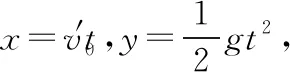
解法四 配方法

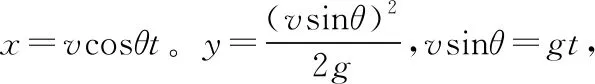
【点拨】物理中的极值问题往往出现“恰好”“最大”“至少”等词语，且有一定的变化条件，在变化的过程中使得某些物理量达到最大或最小，具有情景隐蔽、过程复杂的特点。分析此类问题需要构建模型，用数学语言描述实际运动过程，得到所求物理量的数学解析式，进而进行分析讨论。从上面的分析可以看出，在利用数学知识求解时，设的物理量不同、消去的量不同，讨论的方法就不同，讨论时的繁简程度也就不同，掌握多种分析方法有利于优化讨论过程，提高得分率。常用的方法有不等式法、Δ判别式法、配方法、三角函数法、求导法等。

二、数学极值问题

【例2】如图2所示，质量为M=1.92 m的支架(包含底座)上有一水平细轴，轴上套着一根长为L的刚性轻质细线，绳的另一端拴一质量为m的小球(可视为质点)。使小球在竖直面内绕细轴做圆周运动，小球做圆周运动过程中支架始终不会离开地面，忽略一切阻力，重力加速度为g。求在最低点小球允许获得的最大速度。

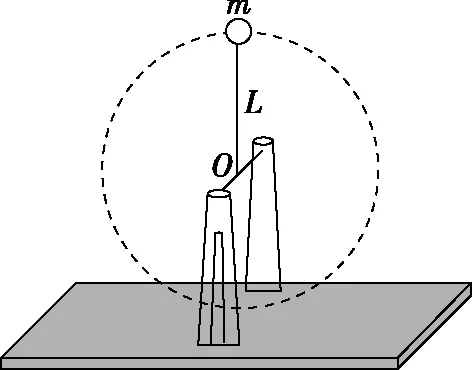
图2

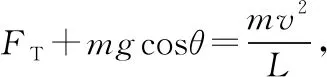
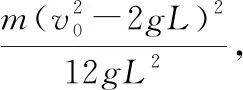
三、物理临界问题

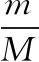
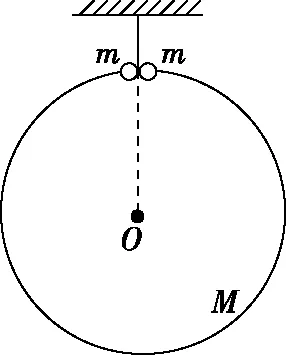
图3

【解析】设当小环与大圆环圆心的连线与竖直方向的夹角为θ时，小环与大圆环间的弹力是FN，要使大圆环有竖直上升的趋势，则小环对大圆环的弹力必须背离圆心(即斜向上)，从而大圆环对小环的弹力必须指向圆心。

对每个小环分析可知

解得FN=mg(2-3cosθ) ①

对大圆环2FNcosθ=Mg②

联立①②得2mg(2-3cosθ)cosθ=Mg③

整理得6mcos2θ-4mcosθ+M=0

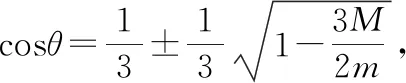
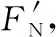
【小结】极值问题一般都具有情景复杂、条件隐蔽的特点。分析此类问题不仅需要很强的建模能力和数学计算能力，还应该注意是否发生质的变化以及是否能满足极值所对应的条件，此类问题能很好体现数学知识在物理中的应用，培养学生思维的严谨性、深刻性，提高学生的理性思维能力和分析问题解决问题的能力。