一个含扩散项的抗病毒药物治疗模型的动态分歧
2021-04-08王会超
李 良, 王会超
(1.四川大学数学学院, 成都 610064; 2.许昌学院数学与统计学院, 许昌 461000)
1 引 言
本文所研究的具有扩散项抗病毒治疗模型[1-7]是在文献[1]中的基础模型后添加扩散项后得到的.原模型只考虑了均匀分布情形,添加了扩散项的模型则更贴近实际.模型的定义如下:
(1)
其中u1表示未感染细胞数,u2表示感染细胞数,u3表示游离病毒数,未感染细胞以常熟率μ生成,以速率γu1死亡,βu1u3表示未感染细胞与游离病毒接触之后变成感染细胞的速率,δu2表示感染细胞裂解死亡的速率,αu3表示游离病毒被清除的速率,Δu表示扩散率,ν表示感染细胞回复至未感染细胞的比率,θu2表示感染细胞裂解后产生病毒速率.抗病毒药物主要以干扰素和一拉米夫啶为代表,其中1-ε表示治疗效果(0<ε<1),1-λ表示核苷类药物阻碍从DNA到CCCDNA循环转移的效率.此外,Neumann边界条件表示细胞和病毒与外界没有进行交换.这里我们只考虑x∈Ω=[0,l]和t>0的情形.
2 预备知识
针对非线性演化方程的抽象形式[2]
(2)
其中λ为参数,我们假设Lλ:H1→H为一个全连续算子,且为扇形算子,H1和H都为Hilbert空间(H1→H紧稠), 并假设Lλ的特征值{βj(λ)∈C|j=1,2,…}满足条件
(3)
由线性全连续场的谱理论可知,H1和H有分解
其中
算子Lλ有分解
另外,非线性项算子G(u,λ)在u=0处可展开成如下形式:
(4)
其中n≥2是一个整数,且Gn(u,λ)是一个n重线性算子.空间Hσ的定义参见文献[3].
定理2.1[3]假设条件(3)成立,且G(u,λ)有形如(4)式的一阶Taylor展开式.那么在λ0附近中心函数Φ(x,λ)可表示为如下形式:
O(|Reβ(λ)|‖x‖k)+o(‖x‖k),
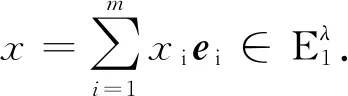
另外,文中需要用到的Morse指数理论可参见文献[3].
3 方程处理
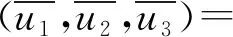
(5)
我们将方程(5)化成形如方程(2)的形式.为此,首先建立空间如下:
H={(u1,u2,u3)∈L2(Ω,R3)}.
令Lλ=A+Bλ,其中
易知,Lλ:H1→H是全连续算子,并且为扇形算子,G(·,λ):H1→H满足条件(4).程化为
现在我们来算方程(5)的特征根和特征向量.
首先,求拉普拉斯算子的特征值.由
可得

其中

易知
且在λ0附近有
再根据线性全连续场谱理论得到
其中
因此,任意u∈H1均可表达为下列形式:
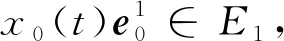
4 结 论
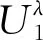
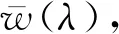
其中
式中涉及的一些量的定义可参见文献[3].
证明 令u∈H1.那么

P1ut=P1Lλu+P1G(u,λ),
P2ut=P2Lλu+P2G(u,λ),
及
化简可得分歧方程为
(6)
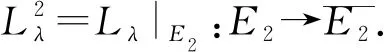
再令
则
其中
因此,
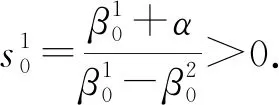
其中
这里0<|λ-λ0|<ε.因此方程(7)的稳态解为
从而方程(5)的分歧解为
进而方程(1)的分歧解为
o(|λ-λ0|).
结论(iii)得证.

当λ0<λ<λ0+ε时,若x0(0)<0,则x0(t)<0,从而
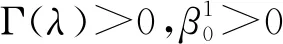
这就证明了方程(1)在区域x0(0)<0是不连续跃迁的.
同样方法可以证明
这就证明了方程(1)在区域x0(0)>0里是连续跃迁的.结论(i)得证.证毕.
注易求得方程(7)的解为
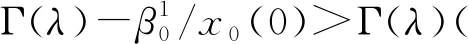



5 数值算例

当λ=0.45时,
从图1可见,Neumann边界条件下的解(u1,u2,u3) →(0.4,0,0),与理论得出的结论一致.
再令λ=0.55,理论得出的奇点分歧解为(u1,u2,u3)→(0.33,0.44,0.41).

图1 λ=0.45时模型(1)的平衡解Fig.1 The equilibrium solutions of Model (1) when λ=0.45
图2表明,方程解(u1,u2,u3)→(0.36,0.17,0.38),此时理论解与数值解误差较小.

图2 λ=0.55时模型(1)的分歧解Fig.2 The birfurcation solutions of Model (1) when λ=0.55
