基于改进多层核超限学习机的模拟电路故障诊断

朱敏， 许爱强， 许晴， 李睿峰

(1.91576部队， 浙江 宁波 315020； 2.海军航空大学， 山东 烟台 264001；3.92228部队， 北京 100010)

0 引言

模拟电路高度集成于现代电子系统并广泛运用于自动控制、通信、供电系统等军用、民用领域。统计数据表明，占比不到20%的模拟部分却集中了整个电子系统中超过80%的故障[1]。因此，模拟电路故障诊断一直是故障诊断领域的热点问题[2]。尽管近几十年来该问题得到持续而广泛的研究，但这些研究多停留于某一环节的理论而未见整套的实际应用方案，事实上该项技术仍远未达到实际应用的水平，其主要障碍除了电路所固有的非线性、组件的冗余性、测试点不足、测量中的不确定性[3-4]外，还在于对于复杂模拟电路所存在的较大规模的高质量故障样本以及高效诊断模型的匮乏[4]。

近年来，基于数据驱动的方法引起了国内外学者的广泛关注，其研究成果主要反映在故障特征提取和分类器设计两个方面[4-6]。当前，模拟电路的故障特征主要分为两大类：第一大类为传统人工提取的特征，包括3种：一是基于电路节点的电压响应(这种方法通常考虑测试性，涉及对测试节点进行优选[5-6])；二是从时频响应曲线中抽取特征(包括峰值增益及其相应的频率和相位[7]，3 dB截止频率[8]等)；三是基于信号处理理论(除最流行的小波特征[9]外，还包括包络特征[10]、高阶统计量特征[11]等)。第二大类特征则来源于由深度神经网络从模拟信号或时频响应曲线中提取的抽象特征[12-14]。分类器方面，近年来基于核的机器学习方法得到了最广泛的关注，其中最典型的方法包括支持向量机(SVM)[15]、核超限学习机(KELM)[16]、相关向量机(RVM)[17]等，核函数及其参数的选取对该类方法的性能有着巨大影响。

人为提取的特征往往需要专业的领域知识，且这种特征与分类器的适配性难以得到保证；受益于深度神经网络对特征和分类器的联合学习能力，深度神经网络自动提取的抽象特征往往效果极佳，但却存在固有缺陷：1)在预训练以及微调阶段需要利用样本反复迭代，学习速度相当缓慢，对工程应用提出了更高的硬件要求；2)具有大量自由参数，其调节缺乏理论指导，因此结果具有偶然性。为提高深度神经网络的训练效率，最近，文献[18-19]将超限学习机(ELM)的思想和深度学习相结合，提出一种多层超限学习机(ML-ELM)，保留了深度学习优势的同时还大大降低了训练时间，但是由于每层ELM的固有特性，结果的随机性仍然存在。文献[20]提出了分层超限学习机(H-ELM)，其主要贡献在于将ML-ELM中的表示学习和分类分成了两个独立阶段。文献[21]则将ML-ELM的最后一层替换为KELM，进一步提升了分类精度并将之应用于航空发动机部件的故障诊断，然而该方法不仅依然需要人为调整每个隐层的节点数量，还需要额外调整核参数及正则化参数，并且这种不彻底的核化方式也没有从根本上改变结果的随机性。

针对现有的模拟电路故障特征提取方法人工依赖程度较高、现有的面向复杂模拟电路的故障诊断方法自动化程度低、实用性差的问题，本文将深度学习与KELM相结合，提出一种基于多层单纯形优化核超限学习机(ML-SOKELM)的故障诊断方法。首先，以文献[4，22]于2018年提出的仿真诊断模型及开发的相应软件为基础获取较大规模的高质量故障样本，再从样本数据出发初步选取故障特征；其次，将ML-ELM的每一层(包括自动编码器层和分类器层)均进行核化，提出了多层核超限学习机(ML-KELM)的概念，彻底避开了传统深度学习中所固有的网络结构(每层神经元数量及初始权重，不包括层数)调整问题，针对由此新产生的少量核参数的设置问题，引入Nelder-Mead单纯形法，对各层核参数进行联合优化；最后，将初选后的故障特征输入训练好的模型，逐层提取特征并获取诊断结果。以国际上最常见的故障诊断基准电路(Sallen-Key带通滤波电路和Biquad低通滤波电路)[17]为例，验证了所提方法相较于其他算法在理论上的优势，并进一步搭建工程中常见的串联稳压电路，通过实测数据验证了所提方法的实用性。

1 多层单纯形优化核超限学习机

1.1 核超限学习机

(1)

式中：‖·‖F表示矩阵的Frobenius范数；‖·‖2表示向量的2范数；β=[β1,β2,…,βL]T是模型输出权重向量，L为隐层层数；h(xi)=[h1(xi),…,hL(xi)]表示隐层神经元对输入样本xi的映射向量，hk(·)表示第k个隐层神经元的激活函数；ξi=[ξi1,ξi2,…,ξim]T表示对应于第i个训练样本的输出误差向量；yi=[yi1,yi2,…,yim]T表示对应于第i个训练样本的理想输出向量；c是正则化参数，并且c∈R+. 基于Karush-Kuhn-Tucker优化条件求解(1)式的优化问题，可得输出权重为

β=H†Y=HT(c-1I+HHT)-1Y，

(2)

式中：Y=[y1,y2,…,yn]T是输入样本对应的目标值向量；H是输入样本的映射矩阵；I是单位矩阵。应用Mercer条件定义核矩阵Ω=HHT，Ω(i,j)=h(xi)·h(xj)T=k(xi，xj)，j=1,2,…,n,可得ELM的核化形式:

f(x)=h(x)HT(c-1I+HHT)-1Y=
[k(x,x1),…,k(x,xn)](c-1I+Ω)-1Y.

(3)

令fp(x)表示第p个输出节点的输出值，则有f(x)=[f1(x),f2(x),…,fm(x)]. 对于给定的测试样本x，其输出类别判定为

(4)

1.2 多层超限学习机

借鉴深度学习的思想，ML-ELM[18-19]由多个ELM自动编码器(ELM-AE)堆叠而成，每个ELM-AE的结构如图1所示。

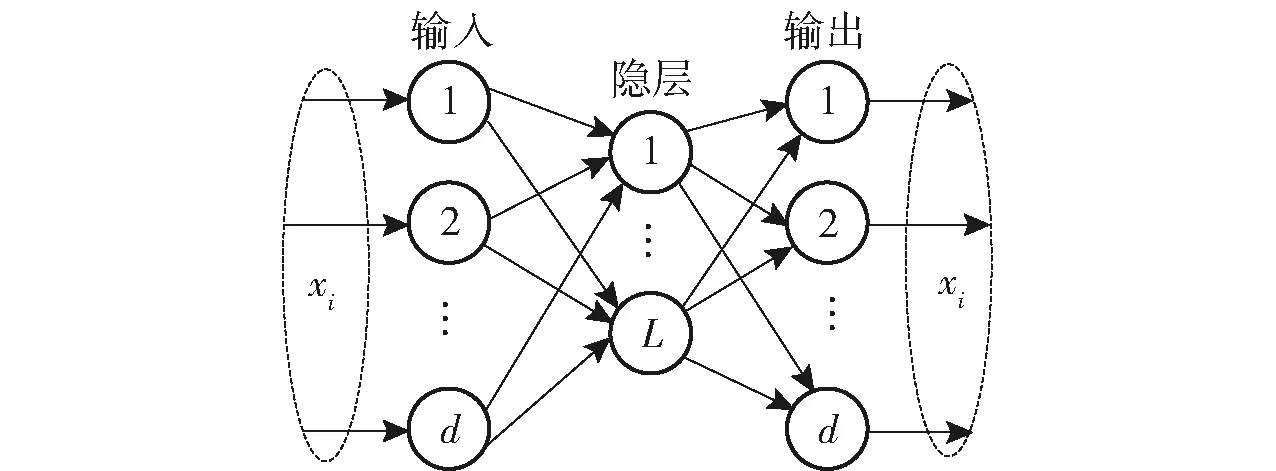
图1 第i个ELM-AE结构Fig.1 Architecture of the ith ELM-AE

H(i)Γ(i)=X(i).

(5)

ML-ELM使用ELM-AE逐层训练时，第i隐层和第i+1隐层的关系为

H(i+1)=g(H(i)(Γ(i))T).

(6)

1.3 多层核超限学习机

在ML-ELM中应用核技巧，本文选用径向基核函数(RBF)将输入矩阵X(i)通过核函数映射到核矩阵Ω(i)，即

Ω(i)=K(X(i),σ(i)),

(7)

式中：K表示与核函数k(·，·)相对应的核矩阵；σ(i)表示其核参数。

(8)

此时，(5)式和(6)式分别改写成：

(9)

(10)

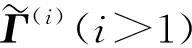
表1 ML-KELM流程

1.4 基于Nelder-Mead单纯形法的核优化

不同核函数的性能表现差别很大，且核函数的构造及相应核参数选取至今没有完善的理论依据[23]。Nelder-Mead单纯形法作为一种解决无约束优化问题的有效方法，因其简单、快速、易实现的特点广泛应用于工程优化计算中[24]。本文将各层核参数向量v=[σ1,σ2,…,σL]视为待优化变量，将L层ML-KELM的训练视为无约束优化问题，运用Nelder-Mead单纯形法搜索其最优值，由此形成ML-SOKELM，具体流程如表2所示。借鉴文献[25]中的核参数设置方法，各层的初始核参数σi设置为各层输入X(i)的平均欧式距离；最大迭代次数MT设为100；为防止过拟合，目标函数f(V)=|ηe(V)-ηt(V)|，其中，ηe(V)为期望的训练误差，ηt(V)为其实际训练误差，V={v1,v2,…,vL+1}。

表2 ML-SOKELM流程

2 模拟电路故障诊断的实施框架

本文使用文献[4，22]提出的仿真诊断模型(SDM)作为模拟电路大规模故障诊断的应用框架，如图2所示。

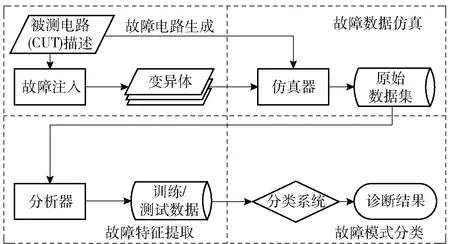
图2 SDM应用框架Fig.2 Application framework of SDM

2.1 故障电路生成

在此阶段，给定CUT描述，变异生成过程根据用户配置产生规定数量的变异体，即向CUT中注入故障并得到相应的电路故障版本。本文涉及的主要变异操作如表3所示。表3中：PCH为软故障变异算子，元件的参数负向偏差(PCH-)和参数正向偏差(PCH+)分别服从均匀分布U(0.1Θ，Θ-2ε)和U(Θ+2ε,2Θ)，ε、Θ分别表示元件的容差值、标称值；ROP、LRB、GRB和NSP为硬故障变异算子；ROP、NSP接入的阻值服从均匀分布U(100 kΩ，1 MΩ)；LRB、GRB接入的阻值服从均匀分布U(10 Ω，1 kΩ)。

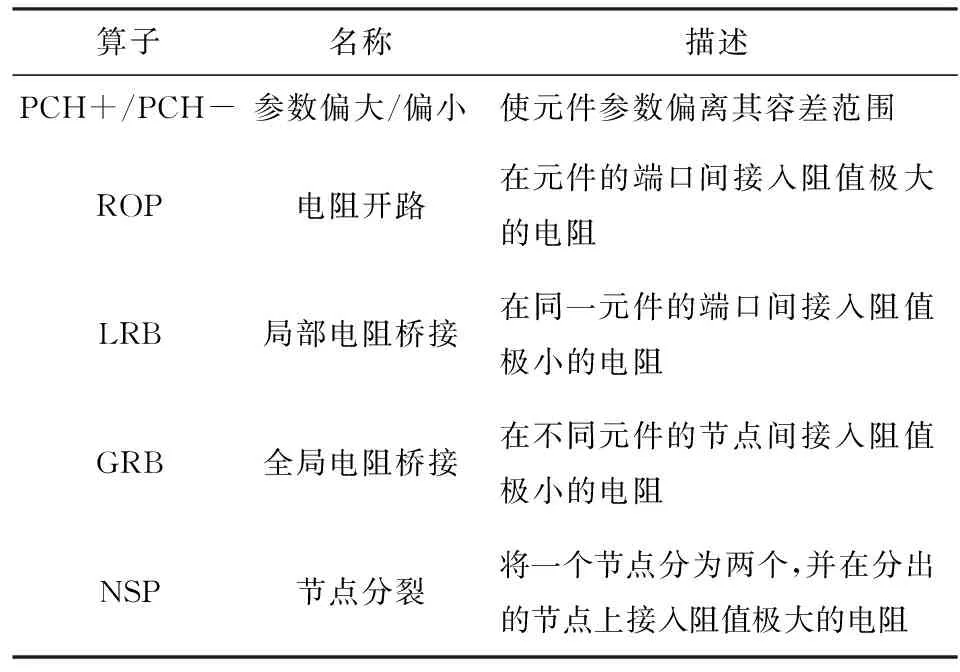
表3 变异算子

2.2 故障数据仿真

将由上一个阶段产生的变异体描述与测试集T中的测试描述信息组合在一起，输入基于Pspice内核的仿真器，从仿真输出文件中解析得到响应信号数据。鉴于元件参数存在一定的容差，假设每个元件参数服从均值为标称值Θ，标准差为σ=tΘ/3的高斯分布，本文中相对容差t设为10%，随后进行Monte Carlo仿真得到各类CUT的仿真数据。

2.3 故障特征提取

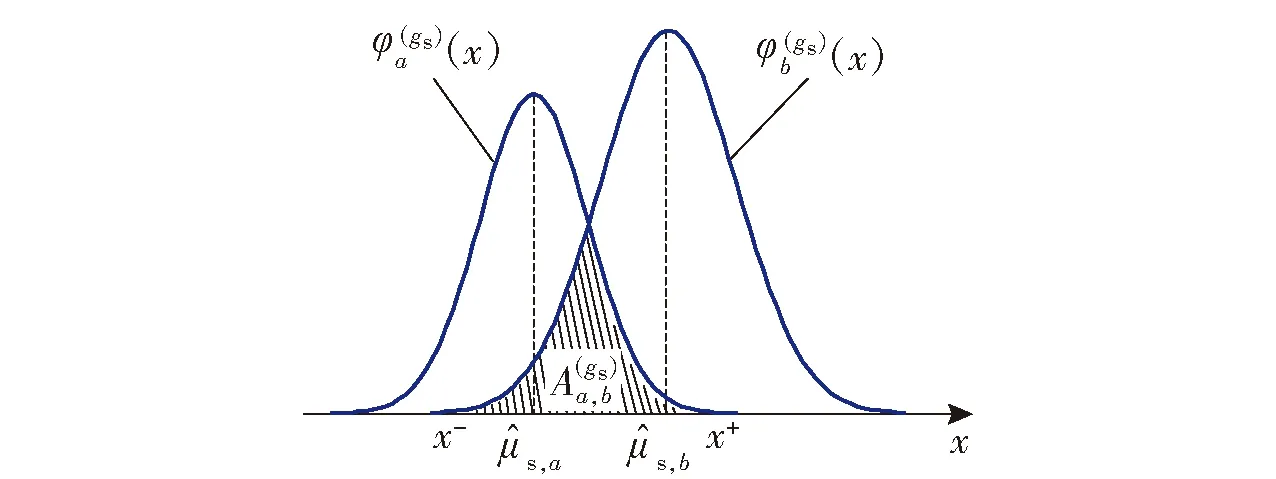
图3 模糊度示意图Fig.3 Schematic diagram of ambiguity

2.4 故障模式分类与评价

首先，根据2.3节特征选择结果从频率响应曲线中提取故障特征形成训练和测试数据集；其次，根据表2流程完成训练；最后，将测试数据集输入训练好的模型进行故障模式分类。借鉴装备测试性中的概念，使用以下指标进行诊断性能的评价：

1) 漏警率(MAR)=发生的漏警数/故障样本总数；

2) 虚警率(FAR)=发生的虚警数/正常样本总数；

3) 故障检测率(FDR)=检测到的故障样本数/故障样本总数；

4) 故障隔离率(FIR)=正确隔离的故障样本数/检测到的故障样本数；

5) 分类正确率(Accuracy)=分类正确的样本数/样本总数。

3 仿真实验

为证明所提方法的有效性，将基于核方法的算法、基于深度学习的算法以及ML-ELM[19]作为比较算法。其中：基于核方法的算法采用最流行的KELM、SVM及Psorakis等[26]提出的多分类相关向量机(MRVM)；基于深度学习的方法则采用最常见的堆叠自编码器(SAE)、深度置信网络(DBN)及结合了深度学习与ELM优势的ML-ELM. 实验中，SVM采用一对一(OAO)法进行多分类，构建的每个SVM的核参数均设为“auto”(意味着对SVM采用启发式方法确定核参数，Matlab 2014a软件中引进的fitcsvm函数可实现该过程)；所有核方法的核函数均采用高斯核，正则化参数与核参数(OAO-SVM与ML-SOKELM除外)通过网格搜索法均从集合[10-6,10-2,…,106]中得到；实验发现，深度学习算法对于模拟电路故障数据在两个隐层时性能较好，为方便比较，本文所有基于深度学习的算法均采用两个隐层的结构。实验电脑配置为：Inter Core i7-4770 CPU，3.4 GHz主频和8 GB RAM.

3.1 Sallen-Key带通滤波电路

首先采用Sallen-Key带通滤波电路来详细分析ML-SOKELM的诊断性能，该电路结构如图4所示。图4中：R1、R2、R3、R4、R5表示电阻；C1、C2表示电容；Vin为激励输入端；GND为接地端；OUT为输出端。注入的14类软故障详见表4，其他非故障元件相对容差设为10%。

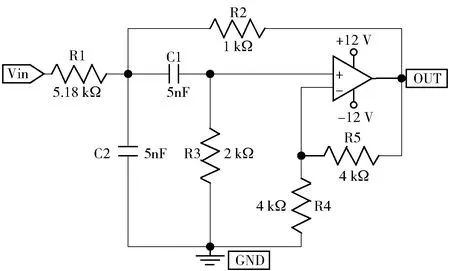
图4 Sallen-Key带通滤波电路Fig.4 Sallen-Key band-pass filter circuit

对CUT的每种故障模式产生200个变异体，将从[0 Hz,100 kHz]频率区间等间隔离散化得到的1 001个激励信号输入到仿真器，得到由3 000个故障样本构成、特征数为1 001的原始数据集。将其按故障类别均分，得到样本数均为1 500的训练集和测试集。借鉴文献[16]的频点(激励)选取方法获取特征集为FT*=[0.001 kHz,9.31 kHz,16.12 kHz,16.82 kHz,17.02 kHz,17.42 kHz,17.62 kHz,18.22 kHz,18.32 kHz,19.32 kHz,20.42 kHz,20.82 kHz,21.92 kHz,23.02 kHz,27.73 kHz,30.13 kHz,30.23 kHz,33.33 kHz,33.43 kHz,70.87 kHz,71.37 kHz]。实验中，ML-SOKELM由两个KELM-AE和一个KELM堆叠而成，将FT*对应的数据集输入各个分类器中，诊断结果的混淆矩阵如图5所示。图5中，模式1～模式15分别对应F0～F14.

表4 Sallen-Key带通滤波电路故障描述

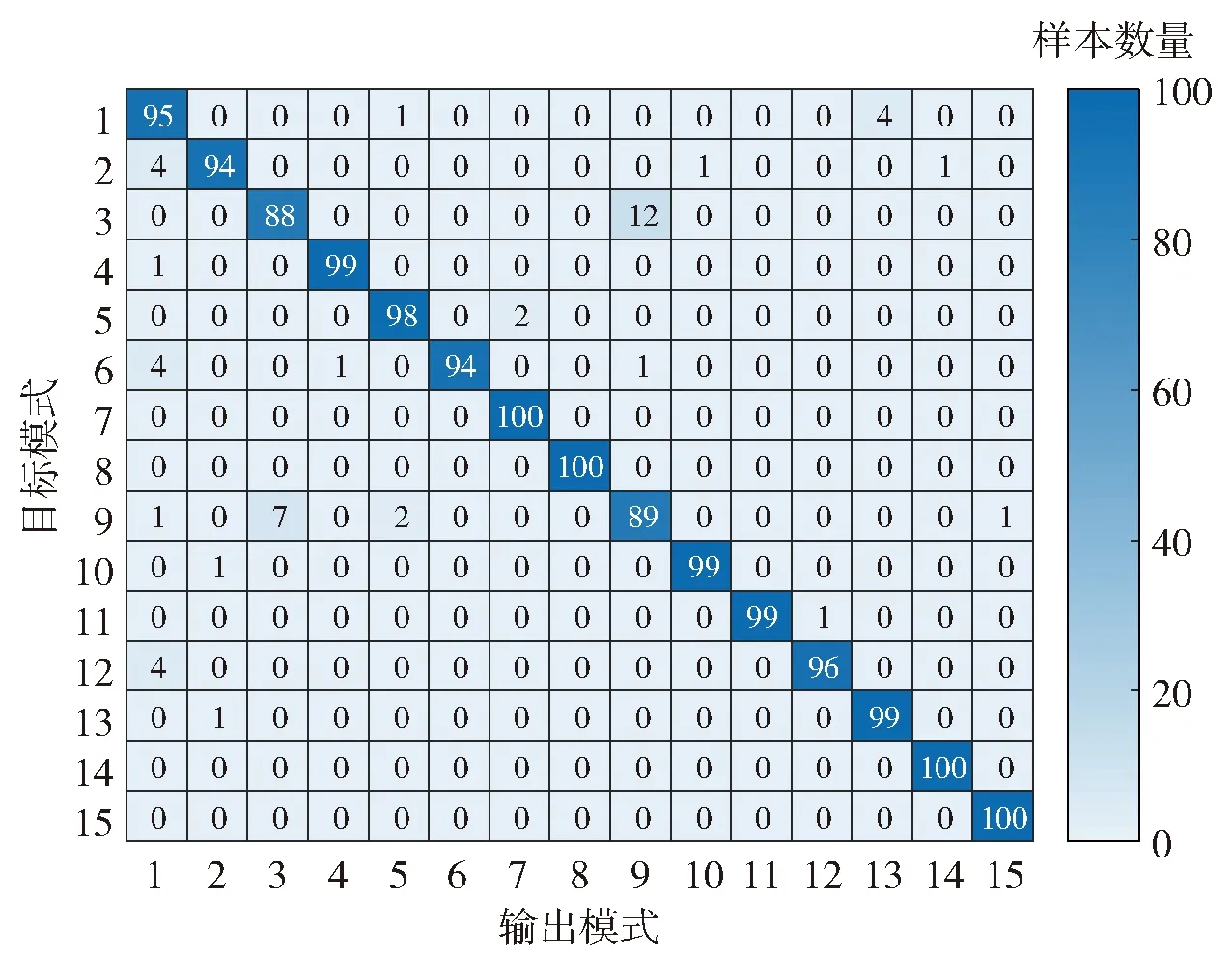
图5 ML-SOKELM的诊断结果Fig.5 Diagnosed results of ML-SOKELM

由图5可知，每种故障模式的诊断准确率依次是95%、94%、88%、99%、96%、96%、100%、100%、85%、97%、100%、98%、95%、99%和100%。其中：诊断准确最低的是F2，仅为88%；F6，F7，F13和F14则达到了100%。从整体上看，ML-SOKELM对本案例中的各类故障模式具有较好的区分能力。

ML-SOKELM与3种常用的核学习算法性能比较结果如表5所示。由表5可知，4种算法除时间花费外，各性能指标差距并不显著。这是因为Sallen-Key带通滤波电路结构相对简单，各故障模式的特征表现相对明显，易于区分。对算法性能进行如下细致分析，以证明其潜力。

表5 与基于核方法算法的诊断性能比较

1) 在诊断准确率上，ML-SOKELM要高于其他3种算法，KELM则是其中表现最差的。

2) ML-SOKELM的FAR和FIR都优于其他3种算法，MAR也仅次于OAO-SVM(高0.07%)，FDR比KELM高0.13%，比OAO-SVM和MRVM分别低0.07%和0.2%，说明所提算法在有效抑制漏警、虚警的同时，还具备较高的故障检测率和隔离率。

3) 时间花费上，KELM显然具备最明显的优势。除KELM之外，在训练阶段，ML-SOKELM由于涉及基于单纯形法的核参数优化过程，训练时间较OAO-SVM略长，但仍然要远远短于MRVM；在测试阶段，ML-SOKELM时效性最佳，OAO-SVM则因为需要对每个二分类SVM进行预测并进行投票统计，时效性最差。

所提算法与两种常见的深度学习算法(SAE、DBN)以及ML-ELM的性能比较如表6所示。为公平比较，SAE、DBN和ML-ELM激活函数均为Sigmoid函数，每层均设定80个节点(通过实验，这样的取值可取得较好效果)。每层RBM及AE预训练次数均为100，第2阶段微调训练次数设为3 000次，批训练(Mini batch)大小设为100. 由表6看到如下内容：

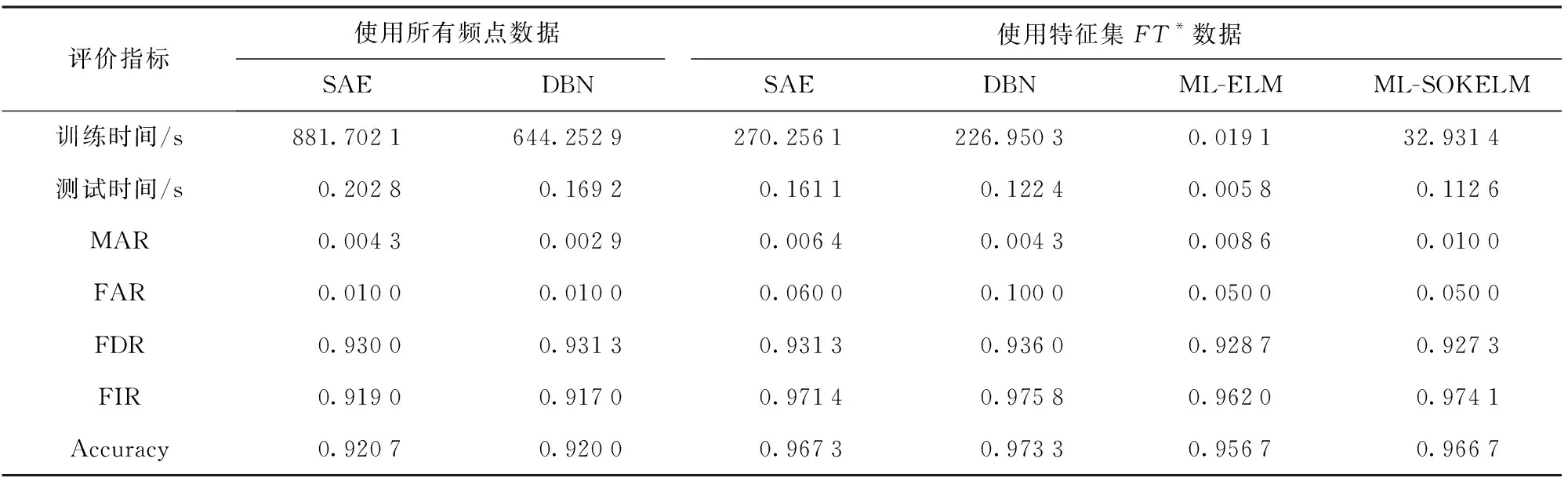
表6 与深度学习相关算法的诊断性能比较

1) 在时间花费方面，ML-ELM和ML-SOKELM均无需对网络进行微调，因此训练时间相对SAE和DBN大幅度缩短，核参数的优化过程则导致ML-SOKELM比ML-ELM耗时略多。

图6 Biquad低通滤波电路结构图Fig.6 Structure chart of Biquad low-pass filter circuit

2) 诊断精度方面，原始数据集经过激励(频点)选取前后，SAE和DBN在原来92.07%和92.00%基础上分别提升了4.66%和5.33%. 一方面说明SAE和DBN的深度结构确实具备在原始幅频曲线基础上直接提取抽象特征的能力；另一方面也证明了特征(激励)初步选取方法可以让抽象特征的提取更为高效。在特征集FT*对应的数据集上进行训练和测试，ML-SOKELM的诊断准确率高于ML-ELM但略低于SAE和DBN，4种算法在其余包括MAR、FAR、FDR和FIR在内的各个指标上并无明显差距。考虑到训练时效性的巨大差距以及对人的主观经验的依赖程度，综合来看，ML-SOKELM明显比其他算法更具实用性。

3.2 Biquad低通滤波电路

为更多地覆盖实际面临的问题，本节对较大规模、同时包含软硬故障的电路进行诊断，以Biquad低通滤波电路为例做进一步的研究，该电路结构如图6所示。图6中：U1、U2、U3表示集成运算放大器；IN表示输入端；n1、n2、n3、n4、n5表示连接节点；1、2、3、4、5表示关键元器件的管脚。注入的29类具有代表性的软硬故障详见表7.

表7 Biquad低通滤波电路故障描述

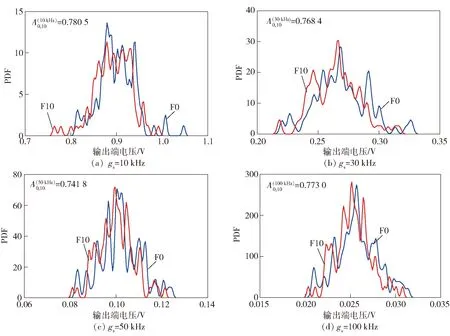
图8 4个频点上F0和F10的模糊度值Fig.8 Ambiguity values of F0 and F10 at four feature points

对CUT的每种故障模式产生100个变异体。以频率为1 Hz～200 kHz(等间隔划分为1 001个频点)的扫频信号作为激励，采集输出端的响应信号作为原始数据，得到由3 000个故障样本构成、每个样本1 001维特征的原始数据集。将其按故障类别均分，得到样本数均为1 500的训练集和测试集。

3.2.1 故障特性分析

对于故障规模较大的复杂电路，某些故障模式的频率响应曲线过于相似，以至于难以精确诊断。以故障F10和正常模式F0为例，其频率响应曲线如图7所示，在频点10 kHz、30 kHz、50 kHz以及100 kHz上对应的概率密度曲线及其模糊度值如图8所示。显然，F10在所有频点上均无法与F0进行区分。由此引出响应曲线簇模糊组的概念。

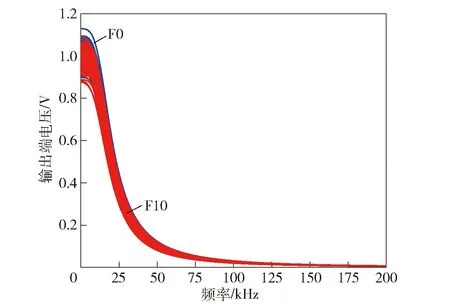
图7 F0和F10的频率响应曲线Fig.7 Response curves of F0 and F10

图9给出了无故障状态F0所对应的AG和不同阈值下所有故障状态的AG. 图9中，δ所在圆的内部所有故障互为AG. 显然，δ=1时不存在AG，随着δ变小，越来越多的故障落入同一AG. 实际诊断时，诊断结果与实际故障在同一AG中，就认为诊断正确。

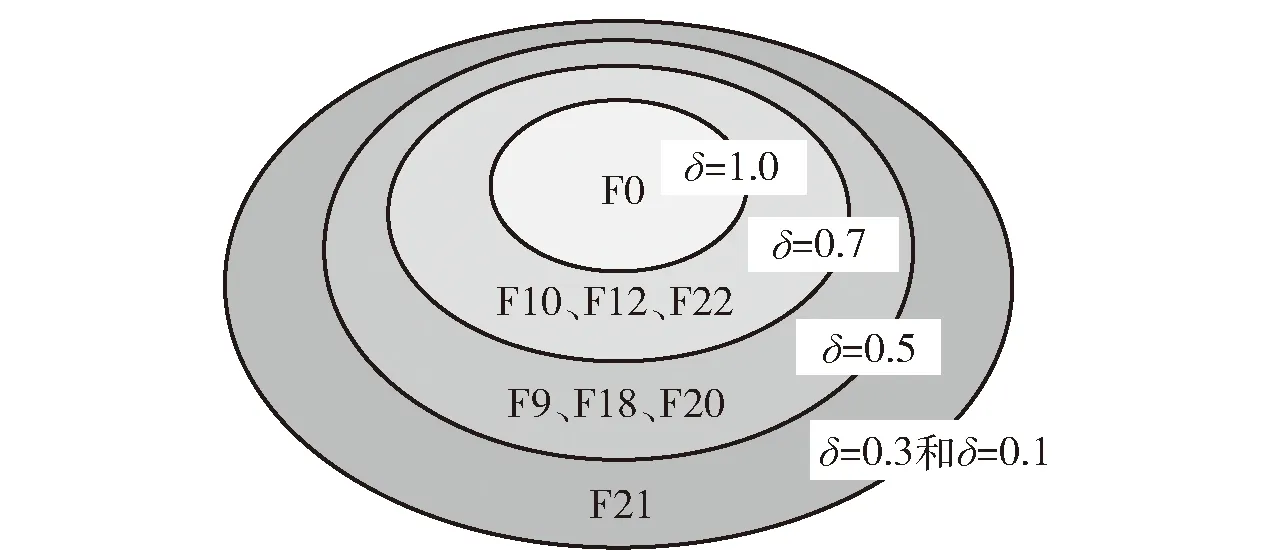
图9 不同δ下F0所在的AGFig.9 Ambiguity group of F0 under different δ

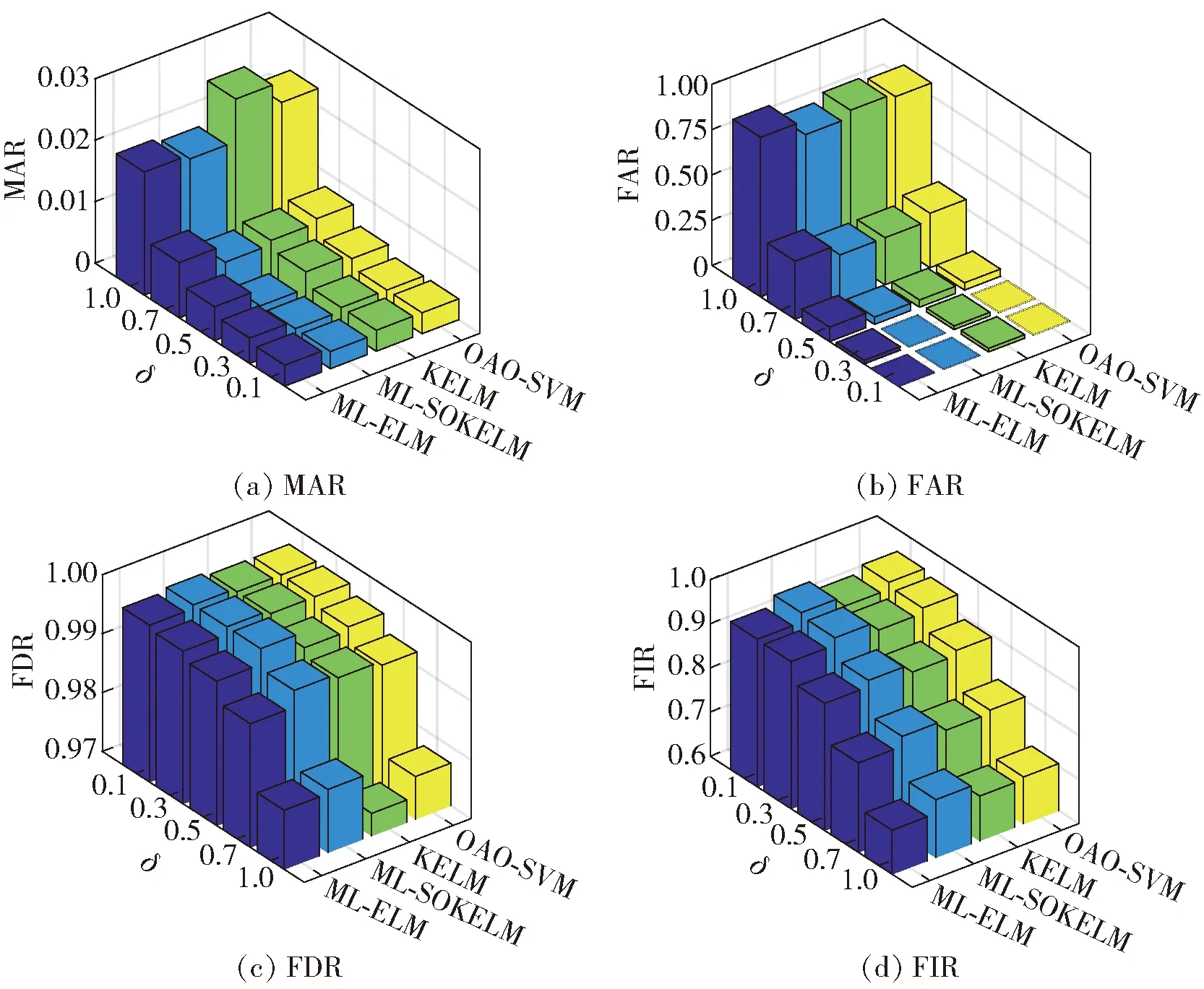
图10 Biquad低通滤波电路诊断结果Fig.10 Diagnosed results of Biquad low-pass filter circuit

3.2.2 诊断结果分析

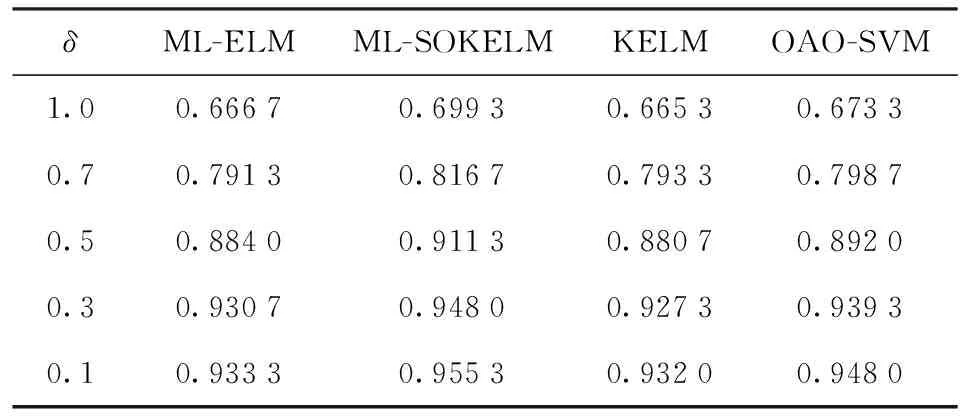
表8 Biquad低通滤波电路诊断准确率比较

由表8和图10可以看到如下内容：

1) 当δ=1时(不考虑AG)，每种方法的诊断准确率均处于最低水平，ML-ELM、ML-SOKELM、KELM和OAO-SVM的FAR甚至分别高达0.88、0.8、0.84和0.82. 这是由于多种元件的故障表现(频率响应曲线)过于接近(例如图7中的F0和F10)，任何分类器都难以将之区分。与表5对比，表9中ML-SOKELM的诊断准确率比其他算法有了更明显的提升，这说明对故障模式不易区分的诊断对象，ML-SOKELM有着更强的分类能力。

2) 随着δ的降低，原本难以区分的故障模式形成AG(如图9所示)，4种算法的诊断准确率、FDR和FIR均随之上升，MAR与FAR则随之降低。

3)在不同δ下，ML-SOKELM均具有最高的诊断正确率、最低的MAR，FDR、FIR和FAR方面也接近或超过其他算法的最优水平。当δ=0.3时，其诊断正确率已高达0.947 3，甚至超过δ=0.1时ML-KELM和OAO-SVM的诊断正确率。

为研究多层结构对诊断精度的影响，分别将ML-SOKELM的层数设为0～6(层数等于KELM-AE个数，0层时退化为KELM)，图11展示了不同模糊度阈值下测试精度随层数的变化关系。

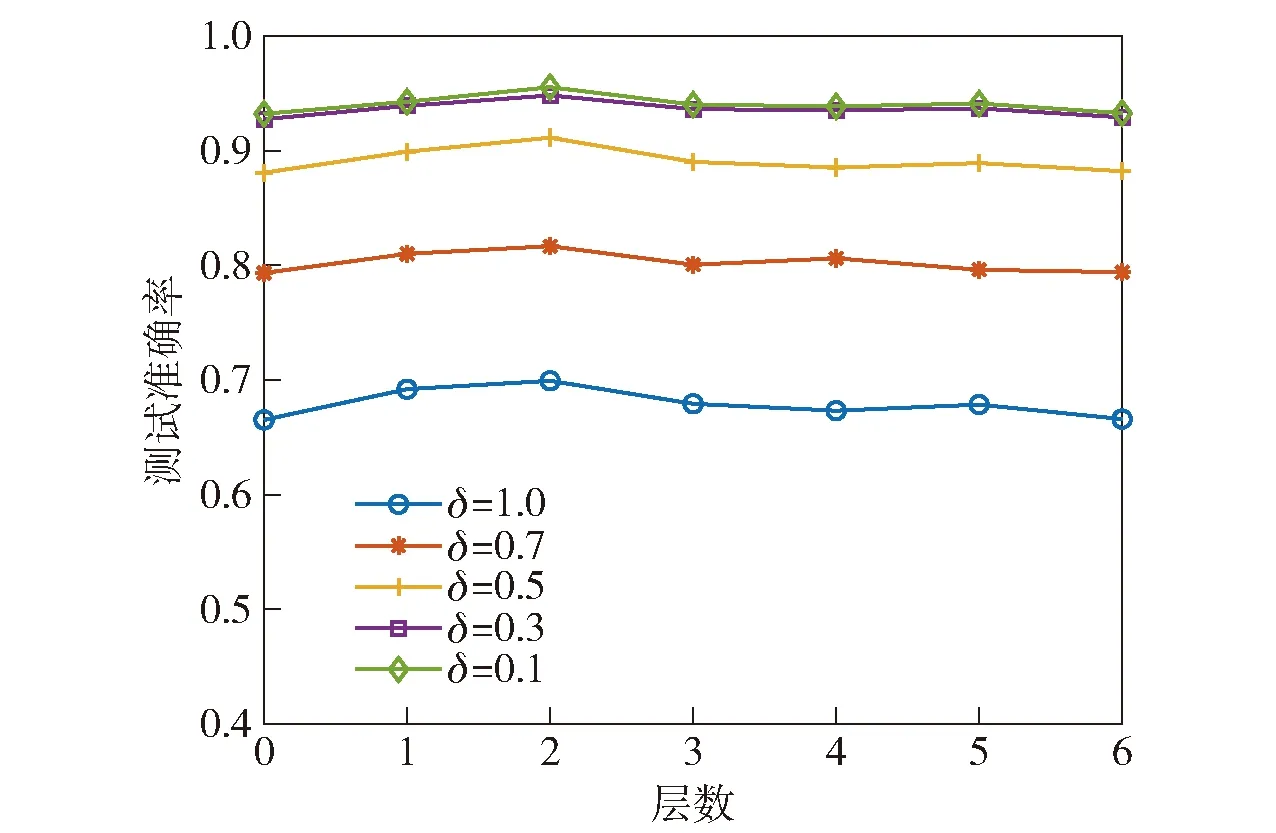
图11 诊断精度随层数的变化关系Fig.11 Variation of diagnostic accuracy with number of layers

显然，ML-SOKELM提取的抽象特征的优异程度不会随着层数的增多而一直增加，对于本文的电

路数据，第2层的抽象特征是最优的，在其基础上进行分类，可以获取最高的诊断精度，随着层数的继续增加，提取的抽象特征反而开始变差，诊断精度出现下降。一种可能的解释是随着层数的增加，模型的复杂度逐渐上升，与训练数据匹配度开始降低，由此产生了不同程度的过拟合问题；从另一方面看，测试准确率的下降并不明显，这说明ML-SOKELM对层数的变化并不敏感，因此，实际应用中简单选择一个较小的层数即可。

从图11还可以看到，当δ减小到一定程度，随着δ的继续减小，诊断精度的提升相当有限。结合图10的结果，建议δ在区间[0.3,0.5]之间取值，因为在这样的区间内，既能得到相对较高的诊断正确率、FDR和FIR，同时还可保持较低的MAR和FAR，又不至于存在太多AG.

3.3 串联稳压电路

本节以实际应用中常见的串联稳压电路为例，通过注入实际故障给出本文方法的实施细节并分析其实用性。该电路结构如图12所示，实物图如图13所示。图12中：Q1、Q2、Q3、Q4表示三极管；D1、D2、D3、D4、D5表示二极管；V1为正弦波信号；RL为负载电阻。该电路共包含20个可更换单元(元器件)，考虑每个元器件的局部硬故障(LRB和ROP)、电容和电阻的软故障(PCH+和PCH-)，共有56个目标硬故障(不包括正常状态)和22个目标软故障。另外，考虑到R3阻值很小，变异配置中不考虑其桥接故障及软故障，最终得到55个目标硬故障和20个目标软故障。

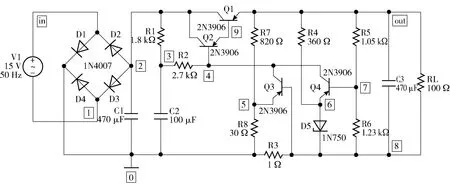
图12 串联稳压电路Fig.12 Serial regulator circuit

图13 串联稳压电路实物图Fig.13 Real serial regulator circuit

基于文献[4]开发的仿真诊断模型及其软件,对CUT的每种目标故障(包含正常情况共计76种)产生100个变异体，并施加幅度为15 V、频率为50 Hz的正弦波信号，分别采集测点1, 2, …, 9, out处稳态响应的最大值和最小值作为初始特征(共20维)，形成训练样本集。

1) 借鉴文献[16]的特征选取方法初步选择特征集，得到来自7个测点的8维特征，即测点1上的最大值和最小值，测点2、3、5、7上的最大值和测点4、9上的最小值。

2) 基于8维特征，对训练样本集中构成AG的

故障进行分析并建立诊断模型。以δ取0.4为例，得到C3开路、Q3的基极、集电极和射极开路4个故障难以与正常状态区分，R2的软故障(PCH+和PCH-)以及C3的软故障(PCH+和PCH-)都难以区分，故将其忽略；依据表2流程完成ML-SOKELM诊断模型的建立。

3) 利用程控电容箱和可变电阻进行软故障的物理注入，以直接断开或用导线短接方式进行硬故障的物理注入；用示波器对上述7个测点上电压的最大或最小值进行测量，将测量值矢量标准化后输入上一步建立的诊断模型；最终得到软故障和硬故障的诊断结果，分别如表9和表10所示，其中，受限于实验的硬件条件(实际上也不可能对实际的硬件电路枚举所有软故障)，各软故障的参数取值仅取一例(容差值取0.1倍的标称值，参数值在软故障参数均匀分布的中心取值)来进行分析。

表9 注入软故障的诊断结果

表10 注入硬故障的诊断结果

考虑到实际物理电路中，非故障元件的参数值是确定的，对同一种注入故障仅能得到一组故障数据，此时，2.4节的部分评价指标将失效。为此，本实验以输出节点的输出值占所有节点输出值之和的比例来近似各个故障的判别概率(如表9和表10的故障结果列所示)。由表9(对于最高判别概率低于60%的，展示了概率最高的前2名)可知：一方面，所有的故障模式都能被准确诊断(对于C3↑和C3↓，由于均属于同一个AG，可以认为诊断正确)，这是因为，在软故障情况下，电路仿真结果与真实实验结果高度一致，故障样本的高质量使得训练的模型尽可能的准确；另一方面，注意到诊断准确概率普遍不高(70%左右)，甚至有部分故障模式的诊断概率极为相近(如表9中加粗部分所示)，一种合理的解释是软故障在客观上距离正常情况较近，故障特征表现并不明显，区分度确实不高。

由表10(该表为每个元器件都展示了一种故障模式，并且已展示所有的判别错误情况，如加粗部分所示)可知，除R3开路、R4短路和Q2集电极开路3个故障，大多数注入故障都能被正确诊断，实际诊断正确率高达94.6%(53/56)。其中：R4短路和Q2集电极开路时，诊断准确概率实际仍处于较高水平(分别是39.9%和40.5%)，接近于第1名(分别是42.5%和42.1%)，诊断发生偏差的可能解释是在仿真诊断模型中，需要用极大的电阻或极小的电阻来近似开路或短路这样的硬故障，这就造成故障仿真样本不能很好地体现实测情况，由此导致最终构建的分类模型出现了偏差；在R3开路情况下，其故障诊断准确概率则远低于第1名(92.8%)，其主要原因可能还要叠加实际使用的仪器精度影响(测量误差增大了实测值与仿真结果的不一致性，在诊断对测量精度较为敏感的故障时造成诊断准确率的快速降低)；对于53种诊断正确的情况，其判别概率至少高于第2名40%，绝大多数甚至达到90%以上，这说明本文算法对于硬故障的诊断具有很高的可靠性。事实上，故障仿真与实际的差异以及测量误差的存在都是难以避免的，再考虑到本文方法极低的人工依赖性以及较高的诊断正确率(94.6%)，有理由认为所提故障诊断方法达到了较高的实用水平。

表9和表10展示了每个注入故障在所提算法下的诊断结果及其可靠程度，为了从整体上验证所提算法在实际电路中的性能优势，下面仍以实用性较高的ML-ELM、KELM、OAO-SVM作为对比算法，在给出不同AG阈值下各方法对实测数据的诊断准确率，如表11所示。

表11 串联稳压电路诊断准确率比较

由表11可以看到，表11的诊断结果与表8是一致的，随着δ的减小，各算法在实际电路中的诊断准确率都在提升。尤其是所提算法，在各个δ取值下，诊断正确率均不同程度地高于其他算法，并且在δ取0.3时就已经达到了最高的诊断正确率，甚至高于其他算法在δ取0.1时的结果，这又一次从整体诊断准确性的角度说明了所提算法的优势。

4 结论

结合深度学习与KELM的优势，本文提出一种基于ML-SOKELM的模拟电路故障诊断方法，相比已有方法，其主要优势在于：

1) 借助最新的SDM测试性框架，考虑了非故障元件的参数容差，完成了从高质量的故障样本获取到特征自动提取到样本分类的一整套诊断方案，并且全程几乎不依赖任何先验知识，具有极强的实用性。

2) 与深度学习算法(包括ML-ELM)相比，ML-SOKELM不需要依赖主观经验来调整网络结构；训练过程中不需要更新权重和偏置，只需维护统一的转换矩阵，大大减少了内存占用。Sallen-Key带通滤波电路的实验结果表明，与SAE和DBN相比，在诊断精度相似情况下，训练时间分别缩短了87.8%和85.5%，测试时间分别缩短了30.1%和8.7%。

3) 与常用的核学习算法相比，ML-SOKELM通过将KELM-AE堆叠形成深度网络结构，能够将数据逐层重新组合，自动提取出更高级的抽象特征。Biquad低通滤波电路的实验结果表明，在不同δ下，均具备最高的诊断准确率，以δ取0.4为例，与KELM和OAO-SVM相比，诊断准确率分别提高了3.47%和2.16%。

为了进一步提升所提方法的实用性，下一步研究方向包括：

1) 本文在单故障假设下应用1阶变异算子来分析电路中的故障。尽管概率很小，但复杂电路中确实存在多故障的可能，尤其是由一个故障引发的其他连带故障，未来可以考虑电路的高阶变异生成。

2) 串联稳压电路的实际实验结果一方面证明了所提方法的准确性和实用性，另一方面也应看到仿真结果与实测结果在硬故障条件下确实存在差异，未来可以用一种仿真与实测相结合的方法，以实物系统的实测数据来辅助构造样本集，这需要研究相关的技术和设备实现高度自动化的故障物理注入。

参考文献(References)

[1] ZHANG C L, HE Y G, YUAN L F, et al. Analog circuit incipi-ent fault diagnosis method using DBN based features extraction[J]. IEEE Access, 2018, 6(5): 23053-23064.

[2] BINU D, KARIYAPPA B S. RideNN: a new rider optimization algorithm-based neural network for fault diagnosis in analog circuits[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(1):2-26.

[3] BINU D, KARIYAPPA B S. A survey on fault diagnosis of analog circuits: Taxonomy and state of the art[J]. AEU-International Journal of Electronics and Communications, 2017, 73:68-83.

[4] TANG X F, XU A Q, LI R F, et al. Simulation-based diagnostic model for automatic testability analysis of analog circuits[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2018,37(7): 1483-1493.

[5] LUO H， LU W, WANG Y R, et al. A new test point selection method for analog continuous parameter fault[J]. Journal of Electronic Testing: Theory & Applications, 2017, 33(3):339-352.

[6] TANG X F, XU A Q, NIU S C. KKCV-GA-based method for optimal analog test point selection[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(1):24-32.

[7] KUMAR A， SINGH A P. Fuzzy classifier for fault diagnosis in analog electronic circuits[J]. ISA Transactions, 2013, 52(6):816-824.

[9] 袁莉芬, 孙业胜, 何怡刚, 等. 基于小波包优选的模拟电路故障特征提取方法[J]. 电工技术学报, 2018, 33(1):158-165.

YUAN L F, SUN Y S, HE Y G, et al. Fault feature extraction method for analog circuit based on preferred wavelet packet [J]. Transactions of China Electrotechnical Society, 2018, 33(1): 158-165. (in Chinese)

[10] LIU Z B, LIU T M, HAN J W, et al. Signal model-based fault coding for diagnostics and prognostics of analog electronic circuits[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1):605-614.

[11] XIE T， HE Y G. Fault diagnosis of analog circuit based on high-order cumulants and information fusion[J]. Journal of Electronic Testing: Theory & Applications, 2014, 30(5):505-514.

[12] YANG H H, MENG C, WANG C. Data-driven feature extraction for analog circuit fault diagnosis using 1-D convolutional neural network [J]. IEEE Access, 2020, 8(1): 18305-18315.

[13] LIU Z B, JIA Z, VONG C M, et al. Capturing high-discriminative fault features for electronics-rich analog system via deep learning[J]. IEEE Transactions on Industrial Informatics, 2017, 13(3):1213-1226.

[14] XU G W, LIU M, JIANG Z F, et al. Online fault diagnosis method based on transfer convolutional neural networks[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(2):509-520.

[15] 廖剑, 史贤俊, 周绍磊, 等. 基于局部图嵌入加权罚SVM的模拟电路故障诊断方法[J]. 电工技术学报, 2016, 31(4): 28-35.

LIAO J, SHI X J, ZHOU S L, et al. Analog circuit fault diagnosis based on local graph embedding weighted-penalty SVM[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 28-35. (in Chinese)

[16] 张伟, 刘星, 许爱强, 等. lp范数约束的模拟电路3层多核故障诊断模型[J]. 兵工学报, 2018, 39(7):1352-1363.

ZHANG W, LIU X, XU A Q, et al. Three-layer multiple kernel fault diagnosis model with lp-norm constraint for analog circuit[J]. Acta Armamentarii, 2018, 39(7):1352-1363. (in Chinese)

[17] 高明哲,许爱强,唐小峰, 等.基于多核多分类相关向量机的模拟电路故障诊断方法[J].自动化学报,2019,45(2):434-444.

GAO M Z, XU A Q, TANG X F, et al. Analog circuit diagnostic method based on multi-kernel learning multiclass relevance vector machine[J]. Acta Automatica Sinica, 2019，45(2):434-444. (in Chinese)

[18] LIYANAARACHCHI L C K, ZHOU H M, HUANG G B. Representational learning with ELMs for big data[J]. IEEE Intelligent Systems,2013,28(6): 31-34.

[19] KASUN L C， YANG Y， HUANG G B， et al. Dimension reduction with extreme learning machine[J]. IEEE Transactions on Image Processing, 2016, 25(8):3906-3918.

[20] TANG J X, DENG C W, HUANG G B. Extreme learning machine for multilayer perception[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016,27(4):809-821.

[21] 逄珊, 杨欣毅, 张勇, 等. 应用深度核极限学习机的航空发动机部件故障诊断[J]. 推进技术, 2017,38(11): 2613-2621.

PANG S, YANG X Y, ZHANG Y， et al. Application of deep kernel extreme learning machinein aero engine components fault diagnosis[J]. Journal of Propulsion Technology, 2017,38(11): 2613-2621. (in Chinese)

[22] TANG X F, XU A Q. Practical analog circuit diagnosis based on fault features with minimum ambiguities[J]. Journal of Electro-nic Testing, 2016, 32(1):83-95.

[23] CHEN X, WANG W, CAO W, et al. Gaussian-kernel-based adaptive critic design using two-phase value iteration[J]. Information Sciences, 2019, 482(6): 139-155.

[24] LAGARIAS J C, REEDS J A, WRIGHT M H, et al. Convergence properties of the Nelder-Mead simplex method in low dimensions[J]. SIAM Journal on Optimization: A Publication of the Society for Industrial & Applied Mathematics, 2006, 9(1):112-147.

[25] IOSIFIDIS A, TEFAS A, PITAS I. Graph embedded extreme learning machine[J]. IEEE Transactions on Cybernetics, 2016,46(1):311-324.

[26] PSORAKIS I， DAMOULAS T, GIROLAMI M A. Multiclass relevance vector machines: sparsity and accuracy[J]. IEEE Tran-sactions on Neural Networks, 2010, 21(10):1588-1598.