井下瞬变电磁探测信号基线漂移校正方法

党 博，王咪咪，杨 玲，李 丹，党瑞荣

（西安石油大学 陕西省油气井测控技术重点实验室，陕西 西安 710065）

0 引 言

瞬变电磁（Transient Electromagnetic，TEM）技术已广泛应用于井下资源勘探、水文地质调查和环境监测领域[1-4]。在井下探测过程中，为了提高探测性能，通常会选择高导磁材料作为探头，进而增强接收线圈的灵敏度[5-7]。然而，测井过程中温度的变化会严重影响高导磁材料的磁导率，使测试曲线的基线产生漂移，从而影响数据反演解释的精度。为了消除基线漂移现象，需要对测试曲线进行温度补偿。传统的温度补偿方法是在仪器探头附近增加温度传感器，利用温度传感器监测井下温度变化，通过对不同温度下的接收信号进行刻度，实现瞬变电磁信号的温度补偿，进而消除曲线中的基线漂移现象[8]。该方法利用井温对测试数据进行刻度，获取不同探测深度的感应电动势，但刻度过程会引入一定的误差，且当探头数较多时，进行温度补偿所需的数据量过大，往往难以实现。此外，曲线拟合法[9]、小波变换法[10]、形态学滤波法[11]等也常被用来校正曲线的基线漂移。其中，曲线拟合法实时性高、准确性好，但算法中拟合点的提取比较困难；小波变换法和形态学滤波法滤除基线漂移后低频成分损失非常大，而测试信号的低频分量中通常也会包含丰富的套管损伤等信息，基线漂移与这些损伤信息的频谱非常接近，在使用这些方法消除基线漂移时，对体现井下介质信息的有用成分会造成一定的损失。

针对以上问题，本文提出了基于经验模态分解（Empirical Mode Decomposition，EMD）的瞬变电磁信号基线漂移校正方法。基于瞬变电磁井下探测模型，分析井下温度变化对高导磁材料磁导率的影响，结合信号的频谱特性，对含有基线漂移的本征模态函数（Intrinsic Modal Function，IMF）进行滤波处理，并利用滤波后的信号重构真实的测试信号。现场实测数据处理结果表明，所提出方法可有效校正温度变化引起的瞬变电磁信号基线漂移现象，提高瞬变电磁测井数据反演解释的精度。

1 瞬变电磁井下探测模型

建立瞬变电磁测井模型，如图1 所示。

图1 井下瞬变电磁探测模型

该模型为同轴圆柱状，共有4 层。其中，1～3 层介质分别为铁芯、空气、套管，第四层为最外层地层，第j层介质所对应的电性参数和半径分别为（εj，σj，μj）和rj，其中，ε为介电常数，σ为电导率，μ为磁导率，r为半径。在该测井系统中，为了提高信号的功率，发射线圈和接收线圈共同绕制在铁芯上，铁芯通常采用高导磁材料。假设绕制在铁芯外侧的接收线圈和发射线圈的匝数分别为NR和NT，线圈半径足够小，则有源区域只包含第一层和第二层，无源区域包含其他介质层。

根据麦克斯韦方程组，引入矢量A和变量x，λ，则非齐次和齐次亥姆霍兹方程为：

式中：k2=μ0εω2-iμ0σω，ω为角频率。令x2=λ2-k2，结合矢量磁势与场量关系式以及复宗量贝塞尔函数的微分性质，则接收线圈的时域感应电动势可以写为[12]：

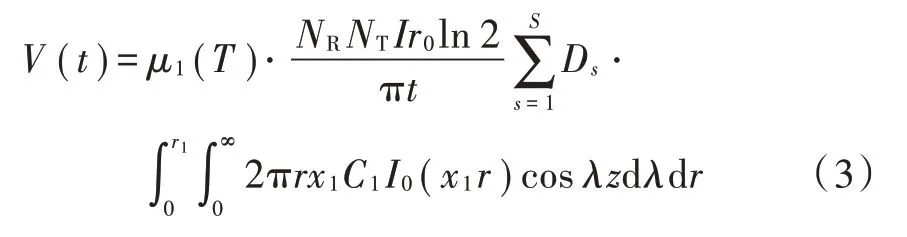
式中：T为井底温度；I为发射电流；I0(xr)为第一类0 阶复宗量贝塞尔函数；z为发射线圈与接收线圈之间的距离；C1为第一层（铁芯）介质的反射系数，可根据电场强度、磁场强度以及边界条件获得；D和s分别为G-S 逆变换的滤波系数和点数。

根据接收线圈的感应电动势可对井下介质的信息进行识别，当温度发生变化时，磁芯的磁导率会相应地发生变化，而其他参数受温度的影响较小，可忽略不计。实际测井过程中，温度会随着深度的增加而升高，从而导致接收线圈的感应电动势出现失真。为了校正井底温度变化对测井信号带来的影响，对高导磁材料的温度特性进行研究。

2 井温对高导磁材料磁导率的影响

在井下探测过程中，井温会随着探测深度的增加而发生变化，一般来说，深度每增加1 000 m，井下温度会增加30 ℃左右，且这一过程并不是线性的，不同地质条件下的温度梯度也不相同。此时，温度的变化会影响高导磁材料的磁导率和饱和磁感应强度，进而影响仪器的井下探测性能。

高导磁材料通常会产生磁滞现象，通过磁场对其反复磁化的过程中，磁感应强度的变化总是落后于磁场强度的变化。为了分析温度对饱和磁感应强度的影响，以软磁铁氧体材料[13]（Mn-Zn 铁氧体）为例，其在25 ℃与100 ℃下的磁滞回线如图2 所示。

由图2 可知，当温度T=25 ℃时，铁氧体的磁感应饱和强度为500 mT；当温度T=100 ℃时，饱和磁感应强度为410 mT。也就是说，铁氧体的饱和磁感应强度是温度的函数，随着井下探测仪器的下放，井温不断升高，磁芯更容易达到磁饱和状态。这种饱和状态的差异会对瞬变电磁发射产生较大的影响，导致不同温度下的发射信号强度不同。此外，井下温度的变化也会影响软磁铁氧体材料的初始磁导率。初始磁导率是磁性材料的磁导率μ（单位为H/m）在磁性曲线始端的极限值，即：

式中：μ0为真空磁导率；H为交流磁场强度，单位为A/m；B为交流磁通密度，单位为T。

图2 Mn-Zn 铁氧体的磁滞回线

以HP 系列高磁导率铁氧体材料为例，其初始磁导率的温度特性曲线如图3 所示。

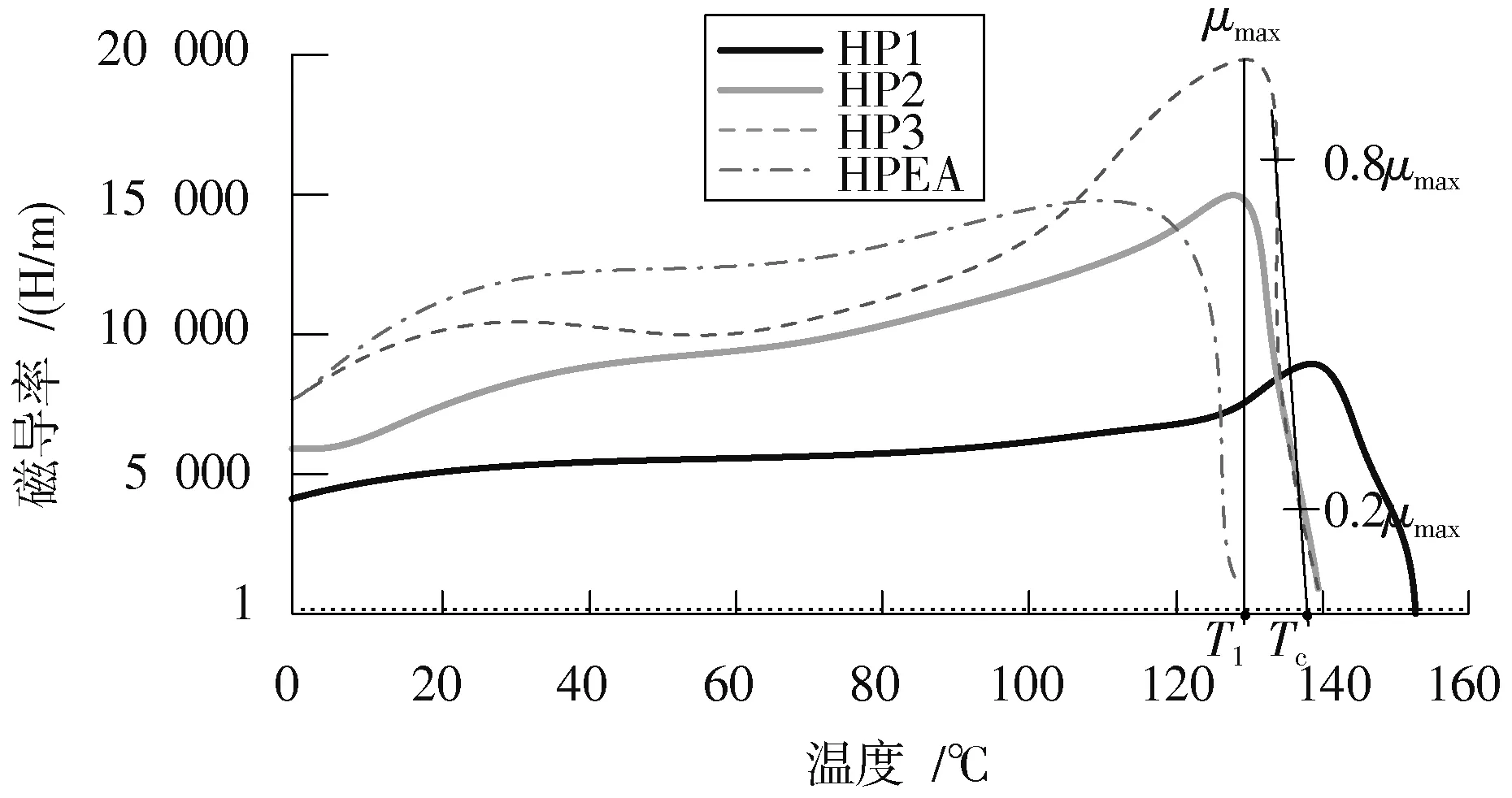
图3 HP 系列高磁导率铁氧体材料初始磁导率温度特性曲线

由图3 可知，铁氧体材料的初始磁导率随温度不规律变化，是温度的复杂函数，不同材料的μ-T特性也不相同。随着温度的升高，铁氧体的初始磁导率达到一个峰值μmax，对应的温度为T1，当温度高于T1时，初始磁导率值急速下降至1 左右。0.8μmax和0.2μmax连线与μ=1的交叉点对应的温度，即为居里温度Tc。正是由于探头磁导率随井下温度的改变不规则变化，即便是相同的被测介质，温度的变化也会使接收线圈感应电动势发生改变，从而造成测井曲线的基线漂移，极大程度上影响了数据的反演解释精度。因此，测井曲线的基线漂移校正对提高井下探测性能具有重要意义。

3 基于EMD 的瞬变电磁信号基线漂移校正算法

井下温度的变化会引起测试曲线的基线漂移，严重影响探测性能。由于瞬变电磁井下探测信号具有非平稳信号的特性，因此，采用EMD 算法[14-15]测试曲线的基线进行校正。对接收线圈感应电动势进行分解，找出所有的局部极大值点和局部极小值点，用三次样条函数连接所有局部极大值点和局部极小值点分别作为上包络线U(t)和下包络线L(t)，上下包络线应包含所有数据，且上下包络线的均值可表示为：

接收响应与上下包络线均值的差为：

如果g1(t)是IMF，则g1(t)是第一个分量，如果g1(t)不是IMF，就将g1(t)看作原始信号处理，再对g1(t)进行EMD 分解，得到g11(t)=g1(t)-m11(t)，m11(t)为g1(t)上下包络线的均值，反复筛选l次，如果g1l(t)满足IMF 的条件，g1l(t) 就称为IMF，就有g1l(t)=g1(l-1)(t)-m1l(t)，c1(t)=g1l(t)是原始信号的第一个IMF成分，也代表V(t)最高频率的分量。

从V(t)中分离c1(t)，得到：

将e1(t)视为原始信号，重复上述过程，可得到信号V(t)的第二个IMF 成分c2(t)，以此类推，当eN(t)是单调函数或是一个极小常量时，就无法再提取IMF，停止分解过程。假设分解次数为N，则接收线圈所接收的感应电动势可表示为：

式中：残差eN(t)是感应电动势曲线V(t)的集中趋势，一定程度上可以反映V(t)的基线。IMFs(c1(t),c2(t),…,cN(t),eN(t))分别包含接收线圈感应电动势从高到低不同频率段的成分，高频分量通常表现为噪声，低频部分残余分量体现了信号的缓变趋势。

在井下探测过程中，温度变化非常缓慢，产生的基线漂移通常属于低频信号。残差项eN(t)虽然可被当作最高阶的IMF，但是它不能完全表示基线漂移信号，因为基线漂移信号中含有多个极值和零点，也就是说，基线漂移现象不仅出现在残差项，其余高阶IMF 分量中也会出现。因此，只要去除含有基线漂移信号的IMF，对剩余IMF 分量重构后即可消除基线漂移现象。然而，直接去除含有基线漂移的IMF 分量会造成信号的失真，因为高阶IMF 中也会包含部分低频分量。采用低通滤波器组对含有基线漂移信号的高阶IMF 分量进行处理。

对井下瞬变电磁响应进行采样，采样总点数为M，假定各IMF 分量均值的阈值为δ，δ无限接近0，将n从1取到N，若：

则从分量IMFn(t)～IMFN(t)的均值均偏离零值，即都包含基线漂移的信息，且随着IMF 分量阶数的升高，包含的基线漂移信息越来越多。将低通滤波器组的响应函数分别标记为hq(t)，q=1，2，…，Q，其中，Q=N-n。从残差项eN(t)开始，倒序通过低通滤波器组，则输出信号为：

式中“*”为卷积运算。从原始信号中剔除包含基线漂移信息的IMF 分量，则可重构真实的井下探测信号：

对接收线圈感应电动势进行基线漂移校正后，可还原真实井下探测信号，有效提高数据反演解释的精度。

4 实验与结果

为验证瞬变电磁测井信号基线漂移校正方法的有效性，以临盘xx 井的探伤数据为例，用所提出方法对原始测试曲线进行处理。实验所用仪器的参数如表1所示。

以800～900 m 井段的瞬变电磁测试信号为例，固定采样时间，原始测试曲线如图4所示。

分析图4 可以看出，测试曲线中的接箍信息比较明显，且在830 m 附近可以观测出接收感应电动势明显减小，即壁厚减薄。但是，随着探测深度的增加，测试曲线的基线出现了漂移现象，且包含套损信息的测试段同样会受基线漂移的影响。

在对测试信号进行反演解释时，温度漂移将会导致反演解释壁厚产生严重失真。为了对该井段测试曲线的基线进行漂移校正，对原始测试曲线进行经验模态分解，分解后的各层IMF 如图5 所示。

由图5 可以看出，该原始测试曲线经过经验模态分解后可分为7 层IMF，且频率由高到低，其中，高频分量多包含噪声，低频分量体现测试信号的缓变趋势。为了更好地校正曲线的基线漂移现象，需要对低频IMF进行滤波。本文设定阈值δ=0.001，将图5中IMF1～IMF7的均值与阈值进行比较后，IMF5～IMF7 均包含有基线漂移信息，利用低通滤波器组对其进行处理，处理结果如图6 所示。

表1 瞬变电磁探伤仪现场实验参数

图4 原始测试曲线

图5 原始测试曲线经验模态分解

图6 基线漂移校正后曲线与原始测试曲线对比图

分析图6 可以看出，采用本文所述方法对瞬变电磁测试曲线进行校正后，曲线的基线不存在弯曲现象，且保留了接箍信息和套管损伤信息，可有效提高后期数据处理和反演解释精度。需要说明的是，本文采用的基线漂移基准值为800～900 m 范围内的电动势平均值，在实际测井中，应以井口初始值作为基准值，以保证瞬变电磁解释的有效性。

5 结 论

本文通过建立瞬变电磁井下探测模型，对温度变化引起的高导磁材料的初始磁导率变化进行了分析，并提出基于EMD 的井下瞬变电磁探测信号基线漂移校正方法，结合瞬变电磁信号的频谱特征，对包含基线漂移信号的低频分量进行滤波，最后重构包含真实探测信息的测试信号。实验结果表明，本文提出的方法可实现瞬变电磁测井曲线的基线漂移校正，有效提高了井下瞬变电磁探测信号的反演解释精度。