多传感器信息融合中的状态估计

摘 要：多传感器信息融合技术，是指通过对多传感器系统所获取的大量信息进行分层次、多级别的融合处理，协调拥有多个信号源的复杂应用系统中传感器相互之间的工作，能够得出更加准确、更加完善的结论，也被称为多源数据融合技术。而多传感器信息融合估计，通过利用多个传感器对同一目标进行观测，基于特定的最优融合准则将测量所得数据进行滤波处理，可以得到更精确、更可靠的融合估计结果，其精度要比单一传感器或局部估计精度高，是多传感器信息融合技术的重要组成部分。本文通过一个仿真实例分析比较了集中式融合与分布式融合对导航参数状态估计的效果，说明了状态估计在多源信息融合系统中具有重要的理论与实际应用价值。

關键词：多传感器信息融合;状态估计;联邦滤波器

状态估计融合是最优估计理论与信息融合理论的有机结合，主要研究在估计系统状态变量的过程中，如何从带有随机误差的多个观测数据中提取出有用的信息，最优的估计某些状态变量，是主要针对信息融合系统中的状态估计问题。大部分多传感器信息融合系统，特别是多传感器多目标跟踪系统在进行估计融合之前要进行数据关联，以决定来自不同传感器的那些数据是属于同一个目标的同一类信息。尽管同源信息与异源信息的特征之间存在不同，但是仍能可以实现信息融合，使得所采集到的信息准确，确保信息的有效性[1]。针对多传感器系统中未知的随机噪声和不相关噪声，可以通过设计自校正信息融合滤波器，将基于相关方法得到的噪声协方差带入到融合最优滤波器中。

1 发展现状

在1973年，美国防部基于声纳信号处理系统提出了数据融合的概念，并应用于当时的军事系统中，到了20世纪80年代初期由于传感器及计算机技术的发展推动了信息融合技术迅速发展，西方国家成功研制了多种实用的军事融合系统。进入21世纪以来，国外对信息融合技术的研究投入更多，各国相继在军用和民用领域成立了信息融合技术实验室。我国对信息融合领域的研究起步较晚，始于20世纪80年代，近年来也取得了丰富的理论成果和实际应用效果。

状态估计融合理论是多传感器信息融合的一个重要分支，目前主要集中在研究多传感器信息融合的卡尔曼滤波算法，卡尔曼滤波算法是由Kalman在20世纪60年代提出的。状态估计融合包括集中式滤波结构、分布式滤波结构和混合式滤波结构三种结构[2]。集中式滤波可实现全局最优估计，精度高，但是其须计算高维矩阵的逆，计算量大，且容错性能较差。而分布式滤波结构不仅可以减少计算量，还具备局部跟踪能力，而且可靠性高。1988年，Carlson提出联邦滤波器，它属于一种分布式滤波算法，在众多分布式滤波算法中最受重视，已被美国空军容错导航系统计划选为基本算法[3]。在传统的联邦滤波算法框架下，如果其中某个子系统发生故障，都会通过主滤波器的反馈校正而使得其他无故障的子系统局部滤波器受到影响，进而影响联邦滤波器的估计效果[4]。

卡尔曼滤波在工程实践中获得了广泛的应用，尤其在导航、制导与控制领域尤为重要。然而，卡尔曼滤波要求系统的数学模型和统计特性精确已知，对于实际系统而言，存在模型不准确、随机噪声不确定等问题，这将影响滤波性能，甚至引起滤波发散。针对实际系统中系统模型参数不准确或噪声方差阵未知的情形，提出了自适应滤波。与传统联邦卡尔曼滤波方法相比，自适应滤波算法能有效地降低观测值误差和数学模型不准确对系统的影响，显著提高了组合系统的精度和可靠性[5]。改进融合算法提高融合系统的性能、建立复杂网络下的融合准则和非线性滤波将是状态估计融合的主要研究方向。

2 状态估计融合结构

在多传感器组合系统中，由于系统的状态或者参数往往不能直接测量得到，而需要基于测量数据和其他先验知识来估计，并使估计误差的某个函数达到最小。多传感器信息融合结构分为集中式、分布式和混合式融合结构。集中式融合可以认为是观测量的融合，其融合结构估计结果通常是最优的，但是其计算效率是最低的。而分布式融合结构是状态向量之间的融合，在融合过程中会受到非相互独立系统的过程噪声的影响，其估计结果是次优的，但计算效率更高。

2.1 集中式融合

集中式融合是指将所有测量数据都集中到一个中心滤波器进行处理和融合，又称为量测融合。集中式融合结构不需要各传感器进行目标关联和目标跟踪，它的优点是融合中心可以利用所有传感器原始数据，在融合过程中没有任何信息损失，融合结果在理论上是最优的。但是他的缺点是需要传输链路带宽大，融合中心需要较大处理能力，实现较困难。

在多传感器信息融合系统中，假设有n个传感器进行独立测量，则系统状态方程可描述为：

集中式融合算法有三种实现形式：序贯滤波、并行滤波和数据压缩滤波。序贯处理是指当各观测分量之间没有观测误差的耦合关系时，将量测更新中对观测的集中处理分散对观测各分量组的顺序处理，可以在计算过程中将对高阶矩阵求逆的过程转化为对低阶矩阵的求逆，可以有效降低计算量。

并行处理将所有传感器量测集中形成一个高维观测向量，按新观测方程用卡尔曼滤波实现估计。则新的滤波器的观测方程中各参数为：

数据压缩滤波是为了提高融合中心的计算速度，将多个传感器的观测量根据特定的融合规则，输入到等效传感器，然后将等效传感器输出作为观测量进行滤波。压缩滤波可实现将高维观测数据降维成低维数据，与并行处理相比具有明显的计算优势。等效传感器的量测方程和量测为：

2.2 分布式融合

集中式融合结构虽然性能优异，但是其计算量较大，对融合中心的运算能力要求较高，而且容错率较差，如果系统中某一个传感器故障都会影响最终融合结果。分布式融合结构，是指在各个传感器进行目标关联跟踪后，对每个传感器分别进行预处理，给出局部估计，再送到融合中心进行全局融合，由于各传感器能形成各自局部的状态估计，又称状态向量融合。分布式融合只能做到局部最优而无法得到全局最优。联邦滤波器是一种分布式滤波器，特别适用于组合导航系统。它的容错性能好，滤波精度高，可以达到全局最优估计精度;而且具有局部滤波器的融合算法简单的优势[6]。多传感器信息融合的联邦滤波器可表示为：

2.3 混合式融合

混合式融合是指融合系统中同时存在两种融合结构，既有分布式的子滤波器，又有一部分观测量集中到一个处理其中进行处理与融合。

3 不同滤波结构对比仿真分析

3.1 仿真条件

为对比集中式滤波和分布式滤波在多传感器导航系统中的效果，考虑某目标做匀速直线运动，离散运动模型如下：

其中vi为测量噪声，服从高斯零均值分布，标准差分别为σv1=0.3m，σv2=0.7m，σv3=1m，传感器采样周期为0.1s，仿真时长500s。

3.2 仿真结果

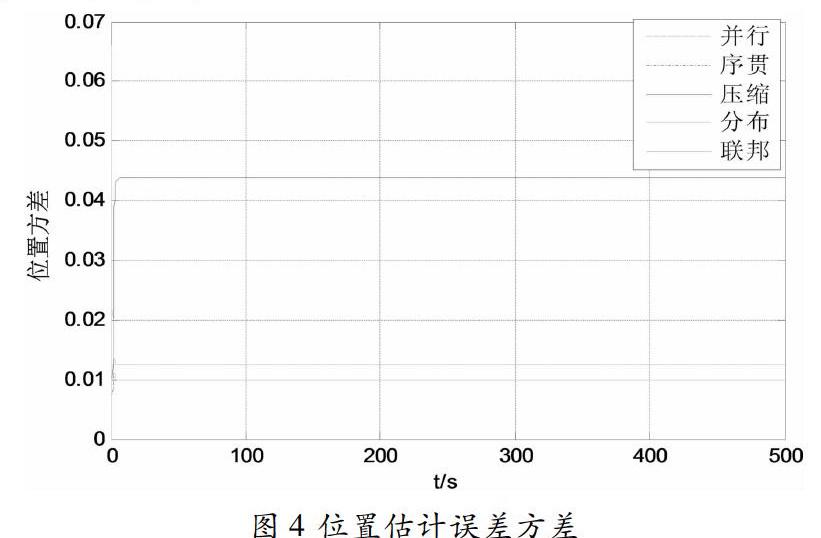
按照以上仿真条件，分别用集中滤波和分散滤波的方法对位置和速度状态量进行估计，得到下面的结果。

由对比结果可知，采用分布式估计方法得到的估计曲线收敛速度更快，超调量更小;并行和序贯两种集中滤波方法的估计结果基本重合，说明两种处理方式在估计效果上是一样的。由估计方差曲线可知数据压缩方法误差最大，因为数据压缩方法在处理过程中损失了部分观测量信息，导致误差变大;联邦滤波方法和分布式滤波方法估计误差方差较小，精度更高。

4 结语

与传统的单传感器系统所获得的信息集相比较，多传感器信息融合系统能够增加系统的抗干扰能力，增加系统的可持续性;减少了系统的模糊性，增加了系统的可信度。本文介绍了集中式和分布式两种多传感器信息融合的结构，并根据仿真算例对比分析了不同滤波结构在某导航系统中的状态估计效果。在多源信息融合时，由于数学模型的偏差和观测信息统计特性的粗差，自适应融合滤波可以处理含有系统模型和噪声统计特性不准确的多传感器信息融合系统状态估计问题，是多传感器信息融合领域的热点方向。

参考文献：

[1]苏振.智能交通控制平台的信息融合技术分析[J].科技风，2017（16）：60-61.

[2]李洋，赵鸣，徐梦瑶，等.多源信息融合技术研究综述[J].智能计算机与应用，2019，9（05）：186-189.

[3]韩强，李保国，陈克川.改进的量测一致性的联邦滤波器两级故障检测[J].导航与控制，2017（03）：61-65.

[4]劉建业，许建新，熊智，王融.区域导航无人机空中基准站的多源信息融合容错导航系统研究[J].导航与控制，2020，19（Z1）：111-118.

[5]段睿，张小红，朱锋.多源信息融合的组合导航自适应联邦滤波算法[J].系统工程与电子技术，2018，40（02）：267-272.

[6]殷德全，熊智，杨菁华，等.SINS/BD紧组合导航系统故障检测算法研究与实现[J].导航与控制，2018（04）：27-32.

作者简介：饶国像（1996— ），男，汉族，江西临川人，硕士研究生，研究方向为惯性导航系统及其应用。