“多维”多尺度重磁位场数据融合方法
2021-04-07刘福香王万银纪晓琳熊盛青
刘福香, 王万银, 纪晓琳, 熊盛青
1 长安大学重磁方法技术研究所, 长安大学地质工程与测绘学院, 长安大学西部矿产资源与地质工程教育部重点实验室, 西安 710054 2 中国自然资源航空物探遥感中心, 北京 100083 3 自然资源部航空地球物理与遥感地质重点实验室, 北京 100083
0 引言
重、磁勘探以其经济快速、绿色环保,覆盖范围广、横向分辨率高等特点在解决地质问题中得到了广泛应用.为了更好地解决某一地质问题,往往在不同时期采集了不同尺度(比例尺、精度)、不同“维度”(卫星、航空、地面、海洋及井中等)的重、磁位场数据.然而,由于存在观测精度和观测位置及数据基准等差异,同一研究区采集的位场数据存在着精度差异、高度差异及数据基准差异等问题.如何将这些不同精度、不同比例尺、不同“维度”和不同基准的重、磁位场数据融合成为统一基准、同一“维度”(后简写为维度)的位场数据就成为重、磁位场数据融合的核心问题之一.根据位场数据融合中数据观测比例尺和观测维度的差异,本文将位场数据融合分为单尺度和多尺度、单维和多维融合问题.单尺度指相同网格距、相同比例尺和相同精度的位场数据,多尺度指不同网格距、不同比例尺或不同精度的位场数据;单维指同一个连续观测面的位场数据,多维指不同高度连续观测面或间断观测面的位场数据.
单尺度重、磁位场数据具有相同的观测位置和观测精度,不同来源的单尺度位场数仅存在数据基准的差异,其融合主要考虑数据基准的统一;而多尺度数据由于存在观测精度或观测比例尺的差异,需要在单尺度数据基准统一的基础上考虑精度校正.
单尺度数据融合方法主要有加权平均和主成分分析法等加权类方法(薛重生等,1997;张丽莉等,2003),其在没有基准差异的单尺度数据融合中计算效果良好,若数据基准存在较大差异,不考虑背景差校正的加权融合则不满足位场数据融合要求.多尺度数据融合方法主要分为两大类,第一类是插值方法,不同精度的数据同时进行插值计算,主要方法有Kriging插值、加权最小曲率插值、Shepard插值、样条插值等(Beylkin and Cramer,2002;刘翔等,2016;刘善伟等,2018a;王虎彪等,2018;柯宝贵等,2018;支澳威和陈华根,2019),此类方法与单尺度数据中的加权计算方法思想类似,能够考虑不同精度数据的差异,但直接插值计算结果会受到多尺度数据基准差影响,不同精度数据边界处形成梯级带;第二类是由不同分辨率的图像融合方法延伸而来,包括基于小波变换(Ranchin and Wald,1993;Deighan and Watts,1997;郭达志和方涛,1997;Kuroishi and Keller,2005;汪海洪,2005;李双成等,2006;Douma and De Hoop,2007;Herrmann et al.,2008;吴健生和刘苗,2008;王海江,2012;杨扬,2013;毕奔腾等,2016;谭沛森,2018;刘善伟等,2018b;陈勐韬等,2020)和Curvelet变换(Candes and Donoho,2005;Nencinia et al.,2007;张恒磊和刘天佑,2011)的融合方法,这类方法将数据分解为不同频段的信息,通过对多来源数据频段的选择和重新组合完成数据背景差的校正和不同精度数据的融合,其在不同分辨率的图像融合中应用效果良好,但由于不同精度的位场数据都包含全段频率的信息,进行频率分解再组合的方法会损失部分高精度数据细节信息,不符合位场数据优选高精度数据的原则.
单维数据不存在观测位置差异,其融合按照上述分类直接考虑单尺度或多尺度融合方法,而多维数据则需在单尺度融合和多尺度融合的基础上再考虑观测空间位置的差异.在实际的数据处理工作中,有学者不考虑观测位置的差异,将多维数据当作单维数据进行处理,这不符合位场数据随空间高度位置变化的规律.
多维数据融合可以通过位场延拓方法实现维度统一后,再进行上述单尺度和多尺度数据的融合计算(吴招才等,2018;余春平,2019);而目前针对多维数据的融合方法主要分为统计法和解析法两大类.统计法主要有最小二乘配置法,利用多维数据建立协方差函数后进行系统偏差估计和精度估计,并在此基础上逐渐发展了一些迭代算法、正则化方法等(Tscherning and Rapp,1974;Forsberg,1987;杨元喜,1996;Tscherning et al.,1998;Strykowski and Forsberg,1998;Tziavos et al.,1998;Olesen et al.,2002;Kern et al.,2003;Huang et al.,2006;翟振和和孙中苗,2010;刘晓刚等,2012;黄谟涛等,2013b;潘宗鹏等,2013;孙文等,2016;王灼华等,2017;赵启龙,2017),该方法能够将不同观测面上的多种类型数据融合起来,但需以足够分辨率的观测数据为基础,且经验协方差函数的选取复杂、大型矩阵的求解过程使得该方法适用性和稳定性受到限制.许多学者致力于解析法的研究(Lehmann,1993;Sideris,1996;Li and Sideris,1997;宁津生等,1998;Kern et al.,2003;郝燕玲等,2007;Eicker,2008;Wittwer,2010;黄谟涛等,2013a,2015;王燚等,2015;吴怿昊等,2016;刘金钊等,2020),该方法在迭代中利用不同观测面上解析计算的位场数据残差修正观测数据或模型系数,引入分步平差、推估内插、迭代下延、点质量等技术,在大区域的重、磁力场计算中应用广泛,能够省去统计法中求解大型矩阵逆的问题,在迭代解析计算中完成多维多尺度位场数据的融合,但迭代中修正模型数据的方法无法全部保留高精度数据,且仍存在迭代稳定性的问题.
针对上述研究现状,本文提出了一套适用于多维多尺度重、磁位场数据融合的实用性方法;对数据维度、基准、尺度的差异,分别采用位场延拓、回归分析、精度加权平均等方法来解决高度不同、基准不同、精度不同或维度不同、尺度不同的重、磁位场数据融合问题,以期得到统一维度、基准及尺度的重、磁位场数据,为进一步处理、反演和解释奠定数据基础.
1 多维多尺度重、磁位场数据融合方法
为了解决多维多尺度位场数据融合问题,需研究尺度统一方法、基准差统一方法(单尺度、多尺度位场数据融合方法)和维度统一方法(多维单尺度位场数据融合方法).
单尺度数据融合方法,采用相关分析和回归分析校正基准差解决数据基准差异;多尺度数据融合方法,采用不同精度数据加权解决观测尺度和观测精度的差异;多维多尺度位场数据融合方法,在以上两类数据融合的基础上采用位场延拓方法解决观测维度的差异(图1).
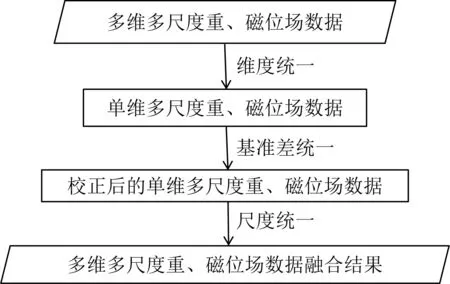
图1 多维多尺度重、磁位场数据融合计算流程示意图Fig.1 The schematic diagram of multi-dimension and multi-scale gravity and magnetic potential data fusion calculation process
1.1 维度统一方法
本文采用位场延拓实现多维多尺度重、磁位场数据融合中的维度统一.本次所使用的位场延拓方法以空间域积分-迭代法(徐世浙,2006)为基础算法,将不稳定的向下延拓问题转换为迭代的稳定向上延拓问题,每次迭代中向上延拓和偏差叠加更新过程是影响计算精度和效率的关键,这两步骤也影响维度统一过程的计算精度和效率,因此成为进行多维数据融合的基础.基于此,本文采用滑动窗口加曲面切片技术(刘芬和王万银,2019)提高计算效率,采用向上延拓滤波技术提高计算稳定性.
(1)位场向上延拓
空间域由原始点(ξ,η,ζ)延拓至计算点(x,y,z)的基本公式(曾华霖,2005)为:
U(x,y,z)=
(1)
以上解析积分在程序实现中使用的是数值积分的矩形积分公式,则(1)式变为:
(2)
其中,Δξ和Δη分别为x和y方向的点距,H(x,y,z,ξi,ηj,ζij)为核函数,其值如(3)式,
H(x,y,z,ξi,ηj,ζij)=
本文采用滑动窗口和曲面切片的向上延拓计算技术(刘芬,2019)提高计算效率.根据位场延拓计算式(式(1))看出,距离越远的场源对计算点产生的异常影响越小.因此根据延拓高度在计算点一定窗口范围内计算,一般选择20倍的延拓高度以上,且小于剖面长度的一半(刘芬等,2019),可在保证精度的前提下减少计算量.
对于延拓高度相同的点(图2中P点和Q点),在相同的窗口大小内,其核函数矩阵是相等的;平面到平面延拓(图2由ΓA到ΓS),可以计算得到窗口内核函数矩阵,然后直接代入式(2)完成每个计算点的延拓.
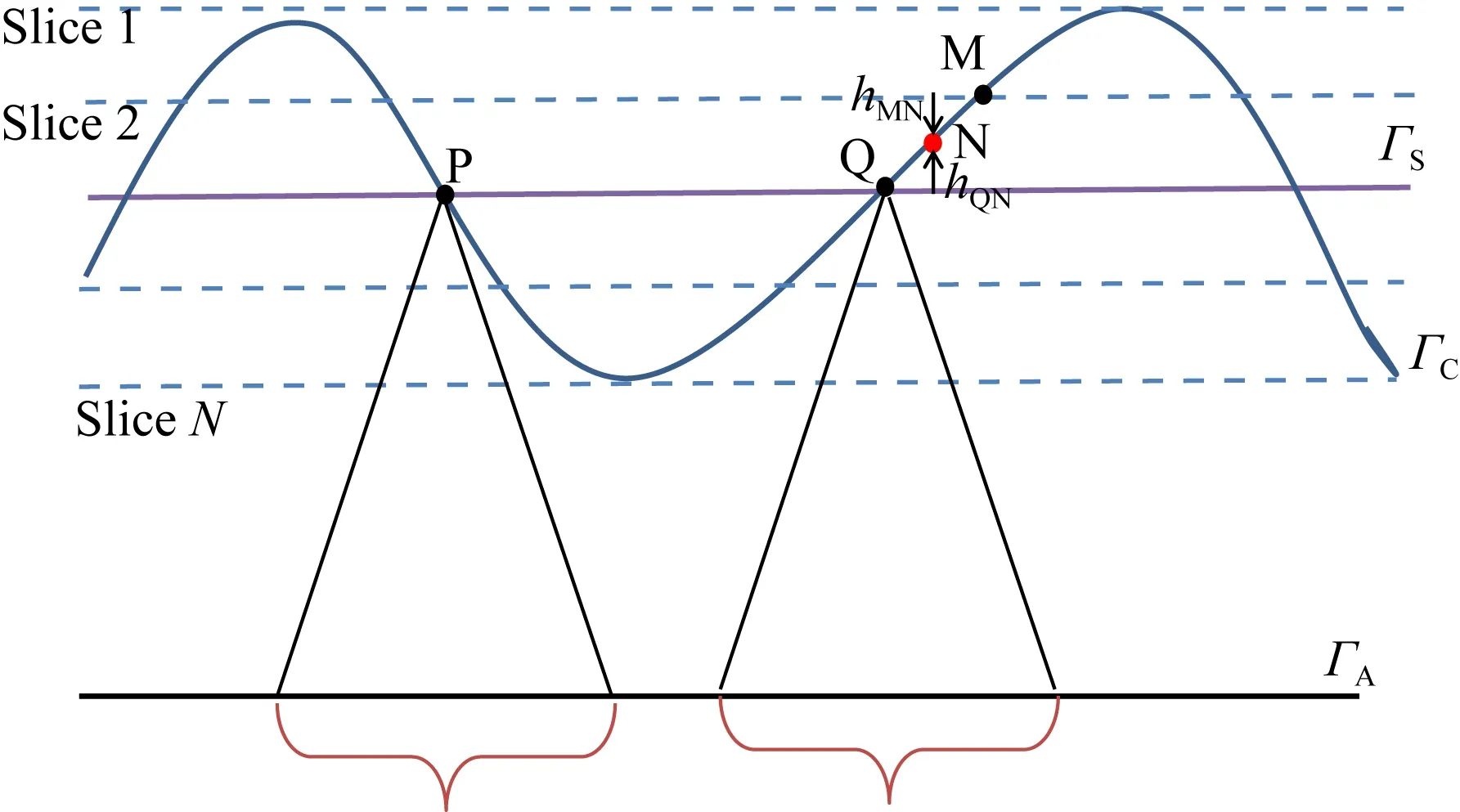
图2 向上延拓中滑动窗口和曲面切片示意图Fig.2 The schematic diagram of sliding window and surface slice in upward continuation
若延拓面为曲面(图2中ΓC),用一组平面切片Slice将其切割后,采用平面的滑动窗口核函数计算方法,首先计算得到每个切片高度上的固定窗口内的核函数矩阵,落在切片上的计算点(Q点和M点)直接代入,分布在切片之间的计算点(N点)的位场值UN则采用反距离加权插值得到,其加权公式(刘芬,2019)为:
(4)
其中,UM、UQ分别为M点和Q点的位场值,hMN、hQN为N点分别与M点、Q点在垂直方向的距离.
由此,通过在空间域向上延拓计算中加入滑动窗口和曲面切片技术可在保证精度的前提下大大减少计算量,提高多维重、磁位场数据融合计算的效率.
设计理论模型检验向上延拓计算方法技术的正确性和有效性.场源由五个直立六面体组成,空间位置和物性参数(表1)及其水平展布位置(图3a)已知;模型基础观测曲面高度起伏为-1000~-2500 m(观测曲面一,z坐标向下为正,图3b),观测平面为z=0 m,x方向坐标范围0~26000 m,y方向坐标范围0~26000 m,两个方向网格间距都为100 m,在观测曲面一和z=0 m平面上正演计算得到重力异常和磁力异常(图3c、d、e、f).
本次测试z=0 m平面数据向上延拓至观测曲面一(-1000~-2500 m)的计算精度和效率.分别进行无窗口的全区域延拓计算、加滑动窗口的延拓计算以及滑动窗口结合曲面切片的延拓计算,分别统计了延拓计算至观测曲面一的重力异常(图4a、b、c)和磁力异常(图4d、e、f)与理论重、磁力异常(图3c、d)的均方根误差、相对均方根误差以及计算时间(表2,配置Intel(R) Core(i5) CPU 2.80 GHz,内存12.0 G的计算机).由表2可以看出延拓计算的重、磁力异常与理论值的偏差都较小,滑动窗口和曲面切片的计算技术能够保证延拓计算的精度;无窗口的全区域的延拓计算耗时最长,加滑动窗口的延拓计算耗时次之,滑动窗口结合曲面切片的延拓计算耗时最短,验证了本次采用的滑动窗口结合曲面切片计算技术能够提高计算效率.这为迭代法向下延拓的多维重、磁位场数据融合中维度统一处理奠定了计算基础.

表1 理论模型体空间位置坐标及物性参数Table 1 The space position coordinates and physical property parameters of theoretical models

表2 理论模型向上延拓计算误差统计表Table 2 The error table of upward continuation calculation of theoretical models
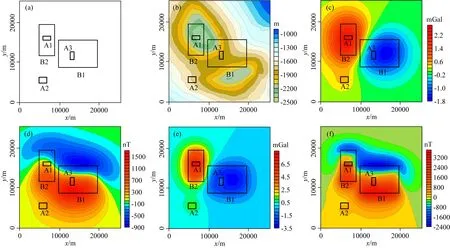
图3 理论模型平面位置、观测面一起伏及重、磁力异常等值线图(a) 理论模型空间位置平面图; (b) 观测曲面一高程等值线图; (c) 模型体在观测曲面一上引起的重力异常等值线图; (d) 模型体在观测曲面一上引起的磁力异常等值线图; (e) 模型体在z=0 m平面上引起的重力异常等值线图; (f) 模型体在z=0 m平面上引起的磁力异常等值线图.图中黑色框线表示五个模型体的边界位置.Fig.3 The plane position of theoretical models, observation surface One and its gravity and magnetic anomaly contour maps(a) The plane position of theoretical models; (b) The contour map of observation surface One elevation; (c) The contour map of gravity anomaly caused by the models on the observation surface One; (d) The contour map of magnetic anomaly caused by the models on the observation surface One; (e) The contour map of gravity anomaly caused by the models on the z=0 m plane; (f) The contour map of magnetic anomaly caused by the models on the z=0 m plane. The black solid lines represent the edge location of the five models.

图5 积分-迭代法向下延拓示意图Fig.5 The schematic diagram of integral-iterative method for downward continuation
(2)位场向下延拓
本文采用积分-迭代法(徐世浙,2006),将向下延拓转换为迭代法的向上延拓.如图5所示,将观测面ΓB上的位场值UB(x,y,z)向下延拓至ΓA主要进行以下几个步骤:



(5)

(6)
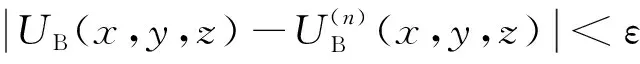

ΔU(n)′B(x′,y′,z′)=

(7)
其中滤波器H就是向上延拓的核函数(式(3));相应地,迭代中的校正更新公式(式(6))变为:


图6 观测曲面二地形起伏Fig.6 The contour map of observation surface Two elevation
采用理论模型测试向下延拓方法技术的准确性和精度.观测曲面二与观测曲面一坐标范围一致,z坐标在观测曲面一的基础上抬升3000 m(z坐标从-3000 m到-4500 m变化,图6),在其正演的重、磁力异常(图7a、b)基础上加入各自数据幅值5%的随机噪声,即重力异常数据噪声均值为0 mGal、幅值为-0.049~0.055 mGal,磁力异常数据噪声均值为0 nT、幅值为-27.488~27.888 nT,利用加噪后的数据(图7c、d)向下延拓至不同的平面(z=0 m、z=-1000 m、z=-2000 m、z=-3000 m),得到的向下延拓结果(图8),计算的均方根误差和相对均方根误差见表3.由图8可以看出,向下延拓计算结果符合位场值随空间变化的规律,随着观测面高度与模型体距离的增加,重、磁力异常的幅值减小.由表3可以看出,原始数据存在噪声时,进行低通滤波处理后向下延拓计算效果良好,各个延拓结果的计算误差小;且随着延拓距离的增加,向下延拓计算精度逐渐降低,这与位场随空间变化规律相符合.

图7 理论模型观测曲面二重、磁力异常等值线图(a) 重力异常; (b) 磁力异常; (c) 加噪声后的重力异常; (d) 加噪声后的磁力异常.Fig.7 The contour maps of gravity and magnetic anomaly of theoretical models on the observation surface Two(a) The gravity anomaly; (b) The magnetic anomaly; (c) The gravity anomaly that added noise; (d) The magnetic anomaly that added noise.

图8 观测曲面二向下延拓计算重、磁力异常等值线图(a) z=0 m重力异常; (b) z=-1000 m重力异常; (c) z=-2000 m重力异常; (d) z=-3000 m重力异常; (e) z=0 m磁力异常; (f) z=-1000 m磁力异常; (g) z=-2000 m磁力异常; (h) z=-3000 m磁力异常.Fig.8 The contour map of downward continuation results from observation surface Two(a) The gravity anomaly on the z=0 m plane; (b) The gravity anomaly on the z=-1000 m plane; (c) The gravity anomaly on the z=-2000 m plane; (d) The gravity anomaly on the z=-3000 m plane; (e) The magnetic anomaly on the z=0 m plane; (f) The magnetic anomaly on the z=-1000 m plane; (g) The magnetic anomaly on the z=-2000 m plane; (h) The magnetic anomaly on the z=-3000 m plane.

表3 理论模型重、磁力异常向下延拓计算误差统计表Table 3 The error table of gravity or magnetic anomaly downward continuation calculation of theoretical models
同时,为检验上述位场延拓计算方法在多维重、磁位场数据融合中的应用效果,本文将向下延拓的计算结果(图8)分别与原始理论重、磁力异常进行融合(图9a、c),同时对比不进行位场延拓直接“融合”的结果(即将多维数据当作单维数据直接处理,图9b、d),并统计融合计算误差(表4).结果显示,在多维数据融合计算中,不考虑数据之间的维度差异直接进行“融合”是不正确,而本文采用的位场延拓方法可以有效统一不同数据的维度差异,计算误差小,是进行多维多尺度位场数据融合的维度统一的有效方法.
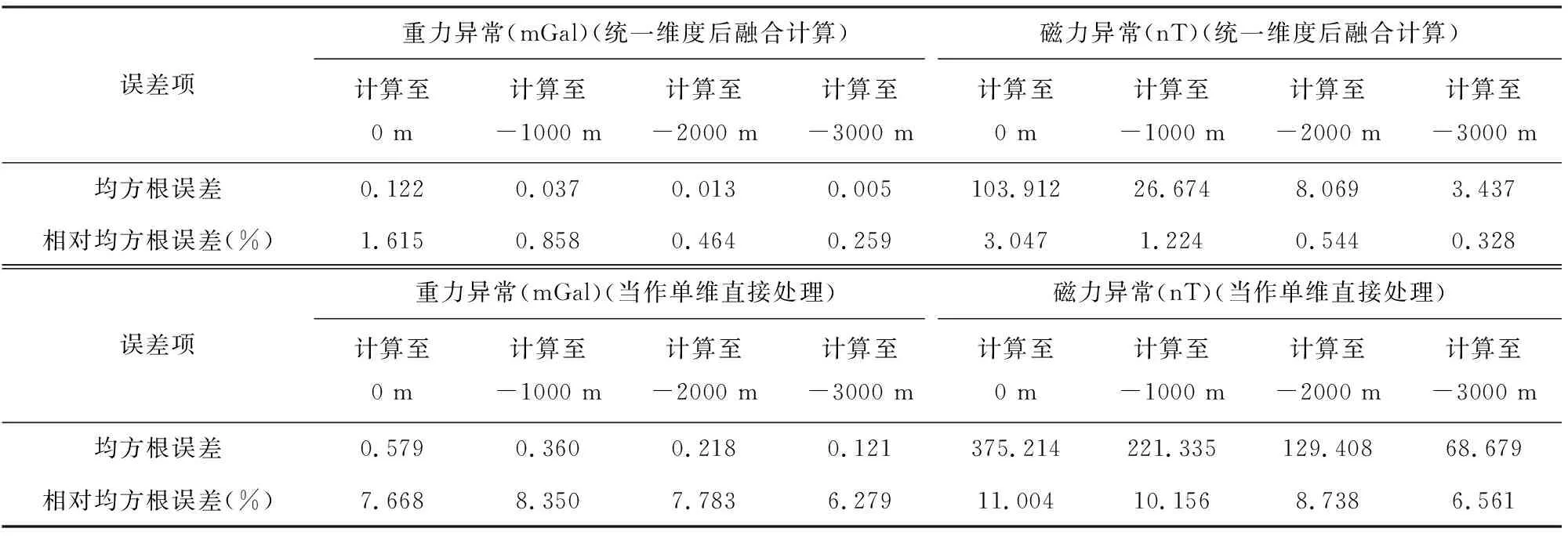
表4 理论模型多维重、磁力异常融合计算误差统计表Table 4 The error table of multi-dimension gravity or magnetic anomaly fusion of theoretical models
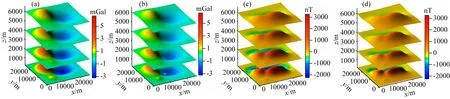
图9 多维数据融合计算重、磁力异常立体图(a) 多维重力异常进行维度统一后的融合结果; (b) 多维重力异常当作单维直接进行处理的计算结果; (c) 多维磁力异常进行维度统一后的融合结果; (d) 多维磁力异常当作单维直接进行处理的计算结果.Fig.9 The 3D surface map of multi-dimension gravity or magnetic anomalies fusion results(a) The fusion results of multi-dimension gravity anomalies after dimension unification; (b) The calculation results of multi-dimension gravity anomalies regarded as single-dimension data; (c) The fusion results of multi-dimension magnetic anomalies after dimension unification; (d) The calculation results of multi-dimension magnetic anomalies regarded as single-dimension data.
1.2 基准差统一方法
本文采用回归分析校正基准的方法技术解决单尺度数据和多尺度数据的基准差异问题.不同组数据间进行回归分析的前提是其存在显著性相关,故需对重叠区的多来源数据进行相关显著性检验.
在单尺度位场数据融合中,由于不存在精度或比例尺的差异,在理论上选取任一组数据作为基准数据都可,其余数据都向此基准数据校正;而对于存在精度或比例尺差异的多尺度数据,须选择精度最高或比例尺最大的一组数据作为校正的基准.
统计学领域中,相关分析是用来考查两组地位平等且无因果关系的变量相互变化的关联关系;回归分析是研究一个因变量与一个或多个自变量之间数量关系的统计方法.应用至位场数据融合中,相关分析中为两组重、磁位场数据,例如不同时期采集的同一地区的维度相同、尺度相同但存在数据基准差异的重力异常,记为gA、gB,采用Pearson相关计算公式,即(9)式,通过计算相关系数r判定两组数据之间的线性相关程度(Pearson,1895):

(9)
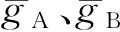
不同来源的重、磁位场数据存在的数据基准差主要源自观测中基点不同,因此在建立回归模型过程中考虑构建较简单的回归模型,如一元线性回归或一元二次回归即可拟合不同数据基准的差异.求解方法是在建立合适的回归模型条件下,以最小二乘法求解模型统计数,获得回归方程,从而依据其中一组作为基准的数据对其他位场数据进行校正.
例如,对于N元线性回归,简单回归模型表示为(Galton,1886):
gA=β0+β1gB+…+βNgB+ε,
(10)
模型中,gA是gB的函数部分加误差项,函数部分反映了数据gB与gA之间的变化对应关系,误差项ε为随机变量,反映了不同时期采集的位场数据gB和gA之间的线性关系之外的随机干扰,β0、β1、…、βN为回归模型的参数,由最小二乘估计得到.
(11)

(12)

根据这一基本原理,进行多组数据之间的一元线性回归分析的处理是选择一个回归的数据体gA(x,y),依次用其他数据gB(x,y),gC(x,y),…,gM-1(x,y)与其进行回归校正,并建立简单线性回归模型形式为:
(13)
即只用数据本身进行校正,得到每个数据体与选取的基准数据的回归系数后,进行相应的计算即完成了数据基准的回归分析校正.

图10 观测曲面三地形起伏Fig.10 The contour map of observation surface Three elevation
选取单尺度理论模型数据测试该回归分析方法在消除基准差中的正确性和有效性.理论模型场源几何参数与物性参数见表1,为模拟不同时期采集的存在数据基准差异的不同范围的单尺度重力、磁力异常数据,设计两个不同观测曲面(观测曲面一和观测曲面三),观测曲面三(图10)是在观测曲面一(图3b)的基础上存在空白区,两观测曲面的重复区占总范围的37%,设计观测面三原始观测异常(数据体2)和观测面一原始观测异常(数据体1)之间存在线性的基准差,其关系式如式(14)所示:
(14)
对两组重力异常(图11a、b)和磁力异常(图11c、d)进行回归分析的基准校正,分别得到校正后重力异常和磁力异常(图12a、b)和计算误差(图12c、d),可以看到其校正后重、磁力异常形态和变化趋势符合位场数据的特点,且形态和幅值均与理论重力异常(图3c)和磁力异常(图3d)吻合很好,计算误差小;重力异常校正计算的均方根误差小于2.008×10-4mGal,相对均方根误差为0.0079%,磁力异常校正计算的均方根误差小于0.135 nT,相对均方根误差为0.0087%,计算精度高,说明本次采用的回归分析能够对单尺度位场数据基准差进行很好的校正.
多尺度理论模型场源几何参数与物性参数见表1.为模拟多尺度数据特点,在观测曲面一的基础上,改变数据间隔为50 m并设置空白区形成观测曲面四(图13a),改变数据间隔为200 m形成观测曲面五(图13e),数据基准差关系式如式(14),同时加入不同大小的随机噪声模拟两者观测精度的差异,重力异常数据噪声均值为0 mGal、幅值为-0.028~0.027 mGal(图13b)和-0.048~0.045 mGal(图13c),磁力异常数据噪声均值为0 nT、幅值为-5.826~5.944 nT(图13f)和-11.861~12.982 nT(图13g);两组数据覆盖范围不同,存在数据重复区(数据重复区占总区域37%).
对重力异常、磁力异常分别进行回归分析校正得到原观测面上背景差校正后的重、磁力异常(图13d、h),可以看到其与理论重力异常(图3c)和磁力异常(图3d)的形态和幅值均吻合很好,基准校正的效果受观测比例尺和随机误差的影响小,重力异常计算的均方根误差为0.013 mGal、相对均方根误差为0.433%,磁力异常计算的均方根误差为3.336 nT、相对均方根误差为0.175%,计算精度较高.同时,进行了不同空白范围的测试,即保持观测面五的范围不变,观测面四范围占总区域比例为9.46%、25.00%、37.86%、47.92%、71.59%,并进行误差统计(表5),可以看出两组数据重叠区不同时,多尺度位场数据基准校正计算结果稳定性好,重叠区覆盖范围越广,校正计算精度越高.
1.3 尺度统一方法
尺度统一需考虑数据观测精度或比例尺的不同,在重叠区需根据精度或比例尺加权计算;为满足后期数据处理和解释的数据需求以及高精度数据的完全保留,需将多尺度数据统一至最高精度的位场数据尺度,本文采用最小曲率方法进行网格化(王万银和邱之云,2011).
重、磁位场数据是地下密度、磁性不均匀体的综合反映,高精度数据包含区域场信息和更丰富的细节信息,为在数据融合能保留高精度数据,在数据重叠区精度加权的原则为:高精度数据权重为1,低精度权重为0;若精度相同,则权重相同(即取平均值).需要注意的是,在进行位场延拓时,延拓的距离越大,计算的误差相应也越大,因此不同高度数据经位场延拓换算至同一个平面或曲面后可信度也有所差别,所以,多维单尺度数据重叠区也存在精度差异,需要加权处理.
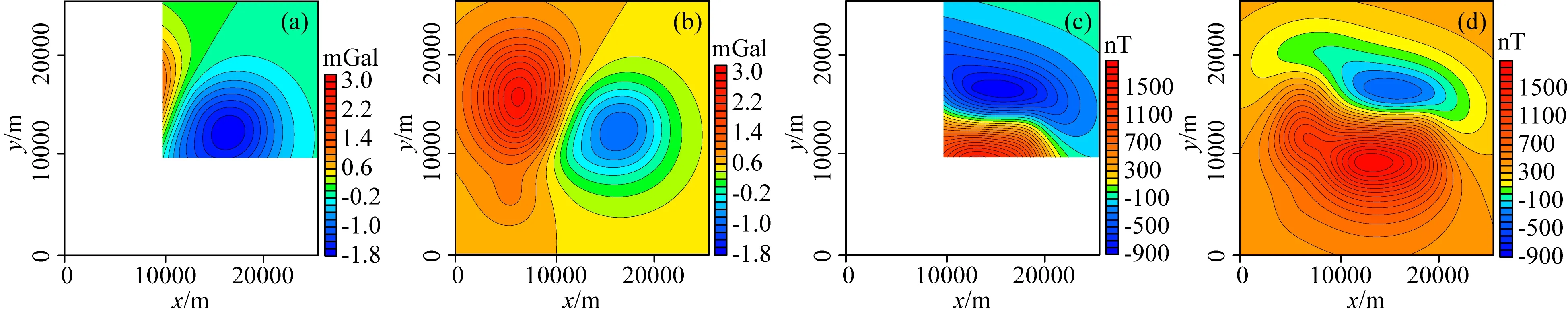
图11 单尺度原始重力、磁力数据等值线图(a) 重力异常一; (b) 重力异常二; (c) 磁力异常一; (d) 磁力异常二.白色区域为数据空白区.Fig.11 The contour map of original single-scale gravity and magnetic data(a) The first gravity anomaly; (b) The second gravity anomaly; (c) The first magnetic anomaly; (d) The second magnetic anomaly. The white areas indicate that there has no data in the areas.

图12 单尺度重力、磁力异常回归分析计算结果及误差等值线图(a) 重力异常回归分析结果; (b) 磁力异常回归分析结果; (c) 重力异常回归分析计算误差; (d) 磁力异常回归分析计算误差.Fig.12 The contour map of regression results of single-scale gravity and magnetic anomalies(a) The regression results of gravity anomalies; (b) The regression results of magnetic anomalies; (c) The error of regression results of gravity anomalies; (d) The error of regression results of magnetic anomalies.

图13 多尺度观测面、原始数据及回归分析结果等值线图(a) 观测面四; (b) 观测面四重力异常; (c) 观测面五重力异常; (d) 重力异常校正结果; (e) 观测面五; (f) 观测面四磁力异常; (g) 观测面五磁力异常; (h) 磁力异常校正结果.白色区域为数据空白区.Fig.13 The contour map of multi-scale observation surface, raw data and regression result(a) The observation surface Four; (b) The gravity anomaly on observation surface Four; (c) The gravity anomaly on observation surface Five; (d) The regression results of gravity anomalies; (e) The observation surface Five; (f) The magnetic anomaly on observation surface Four; (g) The magnetic anomaly on observation surface Five; (h) The regression results of magnetic anomalies. The white areas indicate that there has no data in the areas.

表5 理论模型多尺度重、磁力异常回归分析校正误差统计表Table 5 The error table of multi-scale gravity or magnetic anomaly regression of theoretical models
根据多尺度位场数据融合的方法原理,选取已经完成维度统一和基准差统一的单尺度数据(图12)和多尺度数据(图13d、h),进行单尺度和多尺度融合(图14).由图14可以看出,位场数据融合计算结果能够保留高精度、大比例尺数据的细节信息,同时对研究区内空白区进行了有效补充,不同数据接边位置光滑,没有梯级带和突跳.同时,为测试重叠区范围对多尺度数据融合结果的影响,设计不同重叠区模型测试并统计了融合计算结果的误差(表6),重叠区覆盖范围不同时,融合计算误差均很小,相对均方根误差均小于1%,计算稳定;且重叠区范围越广,融合精度越高.因此,本文提出的多尺度位场数据融合方法在数据重叠区范围不同时均可得到较好的融合计算结果.
最终设计多维多尺度理论模型测试其位场数据融合计算的正确性和有效性.场源参数如表1,设计3个不同高度、不同尺度、数据基准有差异的不同覆盖范围的观测面,观测面一(图3b),观测面六(在观测面一的基础上z坐标增大1000 m,z坐标范围为0~-1500 m,设置空白区),观测面七(在观测面一的基础上z坐标减小2000 m,z坐标范围为-3000~-4500 m;网格间距调整为200 m并设置空白区),以其理论重力异常(图15b)和磁力异常(图15c)进行融合测试.
采用本文的多维多尺度重、磁位场数据融合方法.首先将多维数据以维度统一方法计算至同一个观测面上变为单维数据,接着分别统一单维多尺度数据的基准差异和尺度差异,得到该观测面上的融合结果,利用位场延拓得到了z=0 m、z=-2000 m、z=-4000 m和z=-6000 m四个平面的重、磁力异常(图16).可以看到其融合结果与各个计算面的理论重、磁力异常均吻合较好,重、磁力异常等值线光滑、异常变化趋势一致;随着延拓高度的增加,异常形态变化趋于平缓,符合位场数据随高度变化的规律;融合计算结果与理论异常的误差统计表(表7)显示,其计算至不同高度平面结果均较稳定,计算精度较高,验证了该方法在多维多尺度重磁位场数据融合中的有效性.

图14 单尺度和多尺度重、磁位场数据融合结果等值线图(a) 单尺度重力异常融合结果; (b) 单尺度磁力异常融合结果; (c) 多尺度重力异常融合结果; (d) 多尺度磁力异常融合结果.Fig.14 The contour map of fusion result of single-scale and multi-scale gravity and magnetic anomalies(a) The fusion result of single-scale gravity anomalies; (b) The fusion result of single-scale magnetic anomalies; (c) The fusion result of multi-scale gravity anomalies; (d) The fusion result of multi-scale magnetic anomalies.

表6 理论模型多尺度重、磁力异常融合计算误差统计表Table 6 The error table of multi-scale gravity or magnetic anomaly fusion of theoretical models
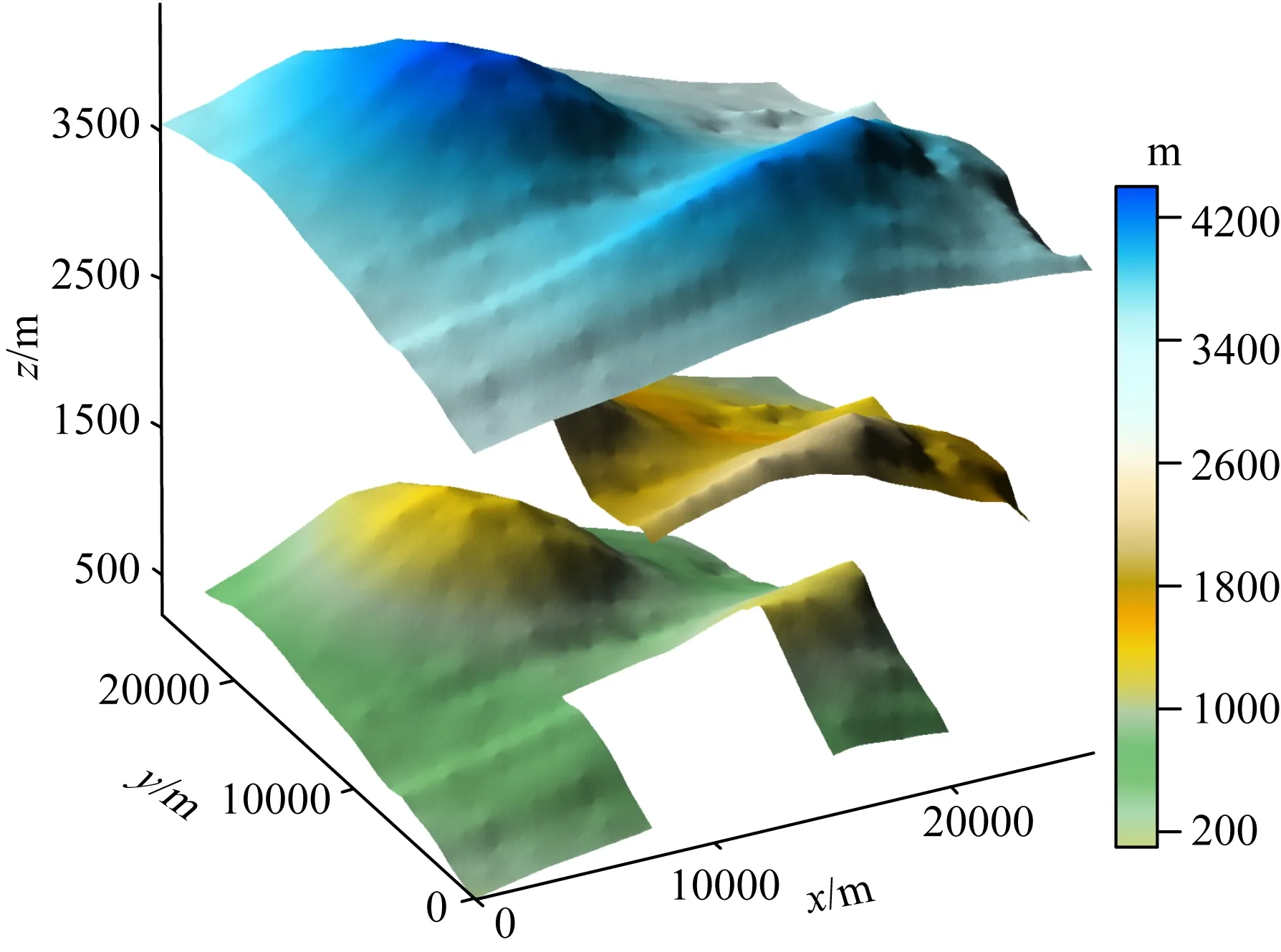
图15 多维多尺度原始观测面起伏Fig.15 The 3D surface map of original multi-dimension multi-scale observation surface
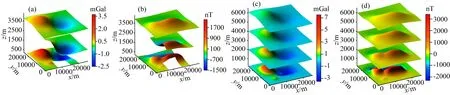
图16 多维多尺度重、磁异常及融合计算结果立体图(a) 观测面重力异常; (b) 观测面磁力异常; (c) 重力异常融合结果; (d) 磁力异常融合结果.Fig.16 The 3D surface map of multi-dimension multi-scale anomalies and fusion results of gravity and magnetic anomalies(a) The gravity anomalies on the observation surface; (b) The magnetic anomalies on the observation surface; (c) The fusion results of gravity anomalies; (d) The fusion results of magnetic anomalies.

表7 理论模型多维多尺度重、磁力异常融合误差统计表Table 7 The error table of multi-dimension multi-scale gravity or magnetic anomaly fusion of theoretical models
2 实际资料处理试验
为检验本文多维多尺度重、磁位场数据融合方法实用性,选取在中国某地航空和地面观测的不同比例尺重力异常数据进行多维多尺度位场数据融合试验.
2.1 单维多尺度重力数据融合试验
选取中国某地1∶50000地面实测重力异常(数据体一,图17b)和1∶200000地面实测重力异常数据(数据体二,图17c)检验单维多尺度重、磁位场数据融合方法的实用效果.两个不同比例尺的地面数据的观测面均为地形面(图17a),地形高度起伏变化范围是747~2623 m,两次重力观测得到了不同比例尺的数据体一(幅值-8~100 mGal)和数据体二(幅值-43~96 mGal),网格化后X和Y方向的网格间距都为150 m,其异常趋势和幅值变化在相同位置上大体一致,但1∶50000的数据反映更多细节信息,而1∶200000数据的变化趋势相对光滑.
利用单维多尺度重、磁位场数据融合方法将两组不同比例尺的重力数据进行融合,以高精度大比例尺数据为基准,将小比例尺数据进行数据基准差校正,相关系数为0.883,回归模型的斜率为0.996,截距(即数据基准差)为5.636 mGal;校正后的小比例尺数据与大比例尺数据进行偏差统计,其偏差平均值为0.017 mGal,均方根偏差为7.546 mGal,相对均方根偏差6.968%,其偏差较小能够保证校正后数据与高精度数据的一致性;之后进行数据融合得到单维多尺度重力数据融合结果(图17d),融合结果重力异常的形态和幅值(33~100 mGal)均与原观测面基本一致,保留了地面高精度的大比例尺数据(图17b)所包含的细节信息,同时用较低精度的小比例尺数据有效补充了高精度大比例尺数据的空白区,融合后的重力异常也符合位场的特点,验证了该融合方法在不同尺度实测重力异常的融合中的实用性.

图17 地形起伏、观测重力异常及融合重力异常等值线图(a) 地形起伏; (b) 数据体一1∶50000地面实测重力异常; (c) 数据体二1∶200000地面实测重力异常; (d) 单维多尺度融合重力异常;黑色点代表观测点.Fig.17 The contour map of topography, measured gravity anomaly and the fusion result(a) The topography; (b) The gravity anomaly measured on the ground at scale 1∶50000; (c) The gravity anomaly measured on the ground at scale 1∶200000; (d) The fusion result of single-dimension multi-scale gravity anomaly; The black points represent the location of the observation points.
2.2 多维多尺度重力数据融合试验
为检验多维多尺度重、磁位场数据融合方法的实用性,在地面不同比例尺重力异常的基础上增加1∶50000航空实测重力异常数据,航空观测面GPS高度为1638~2705 m(图18a),测线间隔为500 m,测点间隔为20 m,重力异常幅值为-43~96 mGal(图18b),X和Y方向的网格化尺寸为150 m,航空重力异常与地面重力异常变化趋势大体一致,但总体幅值较低;两者比较看出,地面数据显示更多细节信息,航空数据观测比例尺虽与地面1∶50000重力数据一致,但其观测精度低于地面1∶50000数据,航空数据主要在覆盖范围和工作效率上更具有优势.
采用本文多维多尺度重、磁位场数据融合方法对数据体一(1∶50000地面重力异常,图17b)、数据体二(1∶200000地面重力异常,图17c)和数据体三(1∶50000航空重力异常,图18b)三组航空和地面实测的不同精度重力异常数据进行融合试验.
数据体一和数据体三融合过程中,航空数据采用位场延拓计算至地面(维度统一)后进行基准差统一,与地面数据对比,其平均偏差小于10-5mGal,均方根偏差为7.379 mGal,相对均方根偏差为6.813%.可以看出,数据体三计算至地面后的精度略高于数据体二(相对均方根偏差为6.968%),但精度相差不大;数据融合重力异常如图19a所示,融合重力异常符合位场数据特征,形态和幅值均与原观测面基本一致,幅值范围为-44~124 mGal,保留了地面高精度数据(图17b)包含的细节信息,同时用效率高、覆盖范围广的航空重力数据有效地补充了地面重力数据的空白区,两者数据相接的位置趋势一致且光滑无梯级带.
根据上述两组数据融合的精度比较结果,该地区三组多维多尺度数据融合时,首先将计算至地面后精度相差不大的航空1∶50000和地面1∶200000重力异常数据融合,加权平均的权重为0.5,得到初步融合结果(图19b),再将其与精度最高的地面1∶50000重力数据进行多尺度融合,即为此三组多维多尺度数据融合重力异常(图19c).
数据体二和三的融合结果(图19c)已经结合了大范围的航空重力数据与小比例尺小范围地面数据的各自优势,经校正后异常形态趋势一致,最终融合结果(图19c)相对于初步融合结果又包含更多地面高精度细节信息;统计初步融合结果校正至地面高精度数据后的偏差,平均值小于10-5mGal,均方根偏差为6.556 mGal,相对均方根偏差为6.054%,由此看出三组数据整体融合的效果优于任意两组数据,同样验证了该思路和方法在多维多尺度位场数据融合中的有效性.
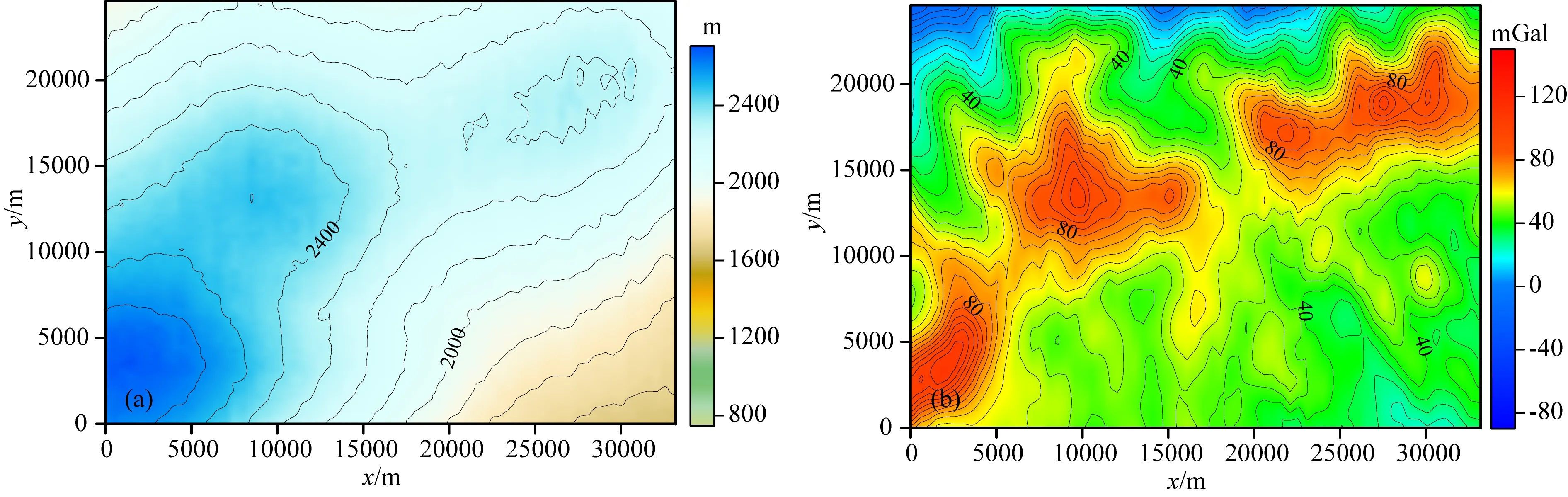
图18 航空观测GPS高度和实测重力异常等值线图(a) 观测面GPS高度; (b) 1∶50000实测航空重力异常.Fig.18 The contour map of observed surface GPS altitude and gravity anomaly measured by aviation(a) The GPS altitude of observation surface; (b) Measured gravity anomaly at scale 1∶50000 by aviation.

图19 多维多尺度融合重力异常等值线图(a) 航空1∶50000与地面1∶50000重力异常融合; (b) 航空1∶50000与地面1∶200000重力异常融合; (c) 航空1∶50000与地面1∶200000、地面1∶50000重力异常融合; (d) 航空1∶50000与地面1∶200000、地面1∶50000重力异常当作单维直接处理结果.Fig.19 The contour map of fusion results of multi-dimension multi-scale gravity anomaly(a) The fusion result of aviation 1∶50000 and ground 1∶50000 gravity anomaly; (b) The fusion result of aviation 1∶50000 and ground 1∶200000 gravity anomaly; (c) The fusion result of aviation 1∶50000, ground 1∶200000 and ground 1∶50000 gravity anomaly; (d) The processing result of aviation 1∶50000, ground 1∶200000 and ground 1∶50000 gravity anomaly regarded as single-dimension data.
另外,为了进一步验证和对比多维数据融合中维度统一的必要性和有效性,本文测试将多维数据当作单维数据不进行位场延拓直接“融合”(图19d),其结果显示在不同数据的接边处存在明显梯级带,且异常值的变化趋势无法达到有效一致,不符合位场变化规律,由此也验证不考虑观测位置高度变化而将多维数据当作单维数据直接“融合”的做法是错误的.本文多维多尺度重、磁位场数据融合方法原理及计算技术对于不同观测比例尺的地面和航空数据进行了有效融合,验证了该方法在实测地面和航空数据融合中的实用性.
3 结论与建议
本文研究了多维多尺度重、磁位场数据融合问题,采用改进的积分-迭代位场延拓方法实现维度统一,采用相关分析和回归分析实现数据基准统一,采用数据精度加权平均的方法实现尺度统一,解决了多维多尺度重、磁位场数据融合中维度、尺度和数据基准差异的问题,提出了一套适用于多维多尺度重、磁位场数据融合的方法.
理论模型测试和实测资料试验显示,该方法适用于航空、地面或海洋观测的重、磁位场数据融合,融合重、磁力异常能够作为后续位场数据处理、反演和解释的基础数据,具有良好的实用价值.本文提出的重、磁位场数据融合的思路也可推广至重、磁力异常各分量或张量数据的融合处理中.
致谢感谢论文评审专家提出的修改意见和编辑对论文的编辑、加工.
