基于深度学习的多STBC盲识别算法

于柯远, 张立民, 闫文君,*, 金 堃

(1.海军航空大学信息融合研究所, 山东 烟台 264001; 2.海军航空大学航空基础学院, 山东 烟台 264001)

0 引 言

通信信号盲识别技术是当今学术界和工程界研究的热点[1],无论是在军事通信领域还是在民用领域,都得到了广泛应用[2-3]。在非合作条件下,对空时分组码信号进行编码盲识别是侦察信号处理中急需解决的难点问题[4],对提升我军电子侦察能力具有重要意义,可以支撑我军对未来战场态势信息与空间态势的实时获取。

目前,有关空时分组码(space-time block code, STBC)类型盲识别的文献大多数都是传统算法,主要分为基于最大似然的方法[5-6]和基于特征参数识别的方法[7-15]。基于最大似然的算法具有较高的识别性能,但是需要预知噪声、调制方式等先验信息,计算复杂度过高。基于特征参数的识别算法不需要对信道进行预估,但对时延和频偏较为敏感且识别算法计算复杂度高,实时性较差,不利于工程化实现。文献[10]提出了一种基于高阶累积量的盲识别算法,但该算法仅能对空间复用(statial multiplexing,SM)码和AL码两种STBC进行识别。文献[13]提出了一种基于KS检测的STBC盲识别算法,但该算法在低信噪比(signal to noise ratio,SNR)条件下识别效果较差。文献[14]提出了一种四阶时延向量的STBC盲识别,通过判断接收信号在不同时延向量下的四阶累积量是否为0识别STBC的编码类型。文献[15]提出了一种基于四阶循环累积量的盲识别算法,通过检测循环频率的方法对STBC进行识别,但该算法的计算复杂度较高且只识别了4种STBC编码。文献[5-15]等传统算法需要人工设定特征值,区分相似度高的编码类型难度较大。

卷积神经网络(convolutional neural networks,CNN)包含卷积计算,是一种具有深度结构的前馈神经网络[16]。CNN仿造生物的视知觉机制构建,可以进行监督学习和非监督学习,并且能够通过多层网络的非线性变换,从输入数据中构造识别特征,避免了人工设计特征的复杂性。

近年来,CNN在调制信号识别、无线电信号检测等领域已取得一定进展[17-19]。文献[17]中提出了一种基于CNN的调制识别模型,该算法能够在低SNR时识别11种调制方式,且识别性能与传统方法的最佳性能相当。文献[18]中提出了一种基于CNN的信号波形识别模型,该模型通过对输入信号进行频域快速傅里叶变换(fast Fourier transform,FFT),将图像特征提取到基于Choi-Williams的时频分布CNN中,能够在高功率噪声下识别8种信号波形。目前,深度学习用于编码识别的论文较少,仅文献[19]提出了一种利用CNN对STBC编码类型的识别算法,但该算法是在时域上对信号进行识别,需要接收端同步,受到一定的条件限制,并且只能够识别出AL和SM两种编码方式。

本文提出了一种基于CNN的多STBC识别算法,是首次在频域上使用CNN实现编码类型识别的算法。针对CNN算法对AL和SM编码识别效果差的问题,对CNN算法进行改进,采用了自相关函数对数据在频域上进行预处理。与时域上的算法相比,不需要接收端同步,大大提高了算法的适用性。自相关CNN算法将待识别的STBC编码类型由4种扩充到了6种,尤其是可对3种相似度较高的STBC3码进行识别。

1 信号模型

1.1 发射信号模型

假设STBC系统具有Nt个发射天线,需要传输的信号序列为S=[s1,s2,…,sn],其中,每个序列中具有n个符号,且传输时隙为L,可表示为S=[Re(ST),Im(ST)]T发射端的信号矩阵矢量可表示为

C(S)=[A1S,A2S,…,ALS]

(1)

式中,Ai(0≤i≤L)表示发射端的STBC矩阵。

1.2 STBC的选取

STBC的正交设计方法较多,且大部分较复杂,目前文献中最多可识别4种STBC[10,12],分别是AL、SM、STBC3r=3/4,1和STBC4,本文将4种码扩充到6种,增加了两种相似度高的STBC3r=3/4,2和STBC3r=3/8码进行区分,这两种STBC3码也是实际系统中常用的编码方式[11]。

本文选取SM、AL、3种STBC3和STBC4等6种STBC作为研究对象,其编码方式如下。

SM码[20]是一组nt个符号通过nt个天线发射的STBC,码矩阵长度L=1:

C(S)=sj,j=1,2,…,NTx

(2)

AL码[20]是一组2个符号通过两根传输天线发射的STBC,码矩阵长度L=2:

(3)

STBC3r=3/4,1码[21]是一组3个符号通过3根传输天线发射的STBC,码矩阵长度L=4:

(4)

STBC3r=3/4,2码[22]是一组3个符号通过3根传输天线发射的STBC,码矩阵长度L=4:

(5)

STBC3r=3/8码[22]是一组4个符号通过3根传输天线发射的STBC,码矩阵长度L=8:

(6)

STBC4r=1/2码[21]是一组4个符号通过4根传输天线发射的STBC,码矩阵长度L=8:

(7)

复正交设计的最大码率可表示为R=N/T,如STBC3在T=4的符号周期内发送N=3个符号(x1,x2,x3),因此STBC3r=3/4,1的码率是r=3/4,同理STBC4的码率r=1/2。

1.3 接收信号模型

假定STBC系统具有Nr个接收天线,假设r(0)为第一个接收符号。在频率选择性信道中,接收符号可以表示为多个发射符号加权求和的形式,STBC信号在经历频率选择性衰落信道后,第k时刻接收到的符号可表示为

(8)

式中,path代表频率选择性衰落信道中存在的路径条数;xi是指第i个时刻的发射信号；hi(p)代表第p个路径的信道系数;w(k)代表信道中存在的高斯白噪声。

2 基于CNN网络的STBC识别算法

2.1 模型框架

针对多个神经网络进行训练后,本文采用的CNN由两个卷积层和两个全连接层组成。两个卷积层和第1层全连接层均采用修正线性单元(ReLU)作为激活函数,第2个全连接层采用SoftMax作为激活函数对6种STBC码进行分类。同时,卷积层和第1个全连接层根据一定的概率将部分神经网络单元暂时从网络中丢弃,以防止过拟合现象的产生,CNN架构如图1所示。输入层为预处理后的I/Q两路的2×128维度的数据,第1个卷积层卷积核大小为1×4,特征映射个数为256个。第2个卷积层卷积核大小为2×3,特征映射个数为80个。第1层全连接层由256个神经元构成,最后一个全连接层神经元个数为6个,对应6种STBC码类型。

图1 CNN架构

表1总结了模型中使用的网络参数,除了第2个全连接层使用SoftMax激活外,其他神经网络层都使用了ReLU激活函数。为了防止过拟合,使用了正则化处理,dropout比率为0.5。训练使用分类交叉熵损失函数和亚当求解器进行。

表1 CNN模型参数

2.2 网络实现

将预处理后的频域输入数据使用Keras中的Reshape函数处理,将2×128维度的编码数据转换为(None,1,2,128)的4D张量,依次代表(样本数、图像高度、图像宽度、图像通道数),作为卷积层的输入。经过两层卷积层的卷积后,输出为(None,80,1,131)的4D张量。在第1层全连接层将4D张量转换为(None,80,1,130)转换为2D张量(None, 256),传递到最后的全连接层中。

在卷积层中,卷积层的输入为X∈RA×B。第j个特征图的卷积网络激活输出[23]可以计算成

(9)

通过式(9)卷积层实现了特征图的卷积,得到了相应的输出特征。本文采用的非线性激活函数θ为ReLU,具体表达式为

ReLU(x)=max(0,x)

(10)

卷积层的输入通道数由输入4D张量的通道数决定。输出张量的通道数由卷积层的输出通道数决定。输出张量的高度和宽度计算公式为

(11)

式中,heightout代表卷积层输出张量的高度;heightin代表卷积层输入张量的宽度;heightkernel代表卷积核的高度;padding代表扫描方式,本文选择的是valid;stride代表卷积核个数;widthout代表输出张量的宽度;widthin和widthkernel分别代表卷积层输入张量的宽度与卷积核的宽度。

卷积层后,输入到第1层全连接层,每次训练随机删除50%的隐神经元,由于每次训练删除的神经元不同,使得每个神经元会尽可能发挥自己的作用,避免过拟合的出现。

二层全连接层采用的是softmax函数,其可以用于多分类过程,将多个神经元的输入,映射到(0,1)之间,每个映射可以看成输出概率,从而进行多分类。假设上一层的输出为{z1,z2,…,zn},softmax层运算公式为

(12)

式中,ki代表代表zi在预测结果中的概率。将输出概率转化为图像显示,就是混淆矩阵,能直观地反映各种编码方式的识别情况。

3 基于CNN算法识别及性能测试

3.1 数据预处理

数据预处理是将原始的输入数据——I/Q采样数据变换为另一种易于CNN进行特征识别的数据类型[24-26],从而充分发挥CNN在特征提取方面的优势,降低计算复杂度,提高对多种相似的STBC类型的识别能力。

对输入信号进行预处理的方式是直接将I/Q采样信号进行FFT处理。原始的I/Q采样信号包括无损信息,适用于作为CNN输入,而FFT是对有限长的I/Q采样数据的无损变换[27]。如:

(13)

式中,N为采样点数。本文中,不做特殊说明时,N=128。

与简单的原始I/Q输入相比,经FFT处理后的频域输入数据可以有效利用CNN在特征提取方面的优势,产生了更好的分类精度。将时域数据变换为频域数据,不需要接收端同步,更加有利于后续CNN的处理和信号识别。

3.2 性能测试与分析

本节对STBC识别的CNN算法性能进行仿真验证。STBC盲识别数据库利用Matlab生成。考虑实际接收信号存在的信道效应和噪声等多因素影响,样本通过Nakagami信道模型来仿真多径、衰落信道。该数据集共计1 000条数据,每条数据有128个符号,将包含SNR信息和6种STBC类型的标签添加在前两列,每条数据共有130个符号。数据集的大小大约是几百万。

实验运行在WIN7系统下,GPU支持CUDA的RTX 2080ti。网络搭建的深度学习库为Keras,后端在Tensorflow框架下,利用Python语言实现了本文模型算法,并进行模型训练与测试。

采用Nakagami-m信道(m=3),噪声为高斯白噪声,仿真采用正交相移键控(quadrature phase shift keying,QPSK)信号调制,SNR设置在-10 ～10 dB,并标记来评估在每个SNR条件下的性能。

本节对文中提出的CNN盲识别算法进行仿真实验,SNR范围为-10～10 dB,每个SNR下进行1 000次蒙特卡罗仿真。如图2所示,6种STBC类型信号随SNR变化的识别概率,在SNR=0 dB时,算法的识别概率稳定在85%左右。图3(a)～图3(e)依次为算法在-10 dB、-5 dB、0 dB、5 dB、10 dB的识别混淆矩阵,反映了6种STBC编码的识别情况。图3中纵坐标轴表示真实标签,横坐标轴表示预测标签。图3中坐标轴0～5依次代表SM,AL,STBC3r=3/4,1,STBC3r=3/4,2,STBC3r=3/8,STBC4 6种STBC方式。

图2 不同SNR下CNN算法性能

从图3中可以看出,CNN算法对于STBC3r=3/4,1,STBC3r=3/4,2,STBC3r=3/8,STBC4这4种编码类型的识别性很好,但是容易将AL、SM两种编码混淆。随着SNR的提升,算法性能的提高主要是对STBC3r=3/4,1,STBC3r=3/4,2,STBC3r=3/8。这3种STBC3编码的识别率逐渐提升,对于SM和AL两种编码的识别能力有所提高,但识别概率仍然较低。

图3 CNN算法在不同信噪比下的识别混淆矩阵

4 自相关CNN算法及性能仿真

4.1 自相关CNN算法

本文提出的CNN算法将STBC编码的识别类型扩充到6种,但存在对SM和AL两种编码识别效果差的问题,算法识别率只能达到85%。针对该问题,对所提出的CNN算法进行了改进。

文献[10]中采用自相关函数对编码矩阵进行处理,提取了信号特征作为分类的依据,自相关函数可增强信号的统计特性,而STBC具有码内相关特性,自相关函数处理后,可以增强STBC内特征向量的显著程度。借鉴该思路,对本文所提出的CNN算法进行改进,在预处理接收信号时,将原始的I/Q两路数据进行自相关函数处理,以提高编码矩阵的相关性,加强后续CNN对信号特征的提取能力。

接收信号的自相关函数定义为

y(k)=E[r(k)r(k)]

(14)

由式(2)可知,连续两个发射的SM信号由独立且分布相同的随机变量组成,自相关函数可表示为

ySM(k)=E(x0x1)=0

(15)

同样,对于AL信号,由式(3)可知,两个连续的时间周期之间存在相关性。因此,相关函数可表示为

(16)

对于AL信号,连续两个时间段内接收到的信号可以表示为

r(0)=h0x0+h1x1+n0

(17)

(18)

自相关函数y(k)可表示为

(19)

自相关函数的FFT可表示为

Y(k)=FFT[yAL(k)]

(20)

对于SM信号,连续两个时间段内接收到的信号可以表示为

r(0)=h0x0+h1x1+n0

(21)

r(1)=h0x3+h1x4+n1

(22)

自相关函数y(k)可表示为

ySM(k)=E[r(0)r(1)]=0

(23)

对自相关函数的FFT可表示为

Y(k)=FFT[ySM(k)]

(24)

由式(14)～式(24)可以看出AL信号与SM信号的区别,AL符号是部分相关的,而SM符号不是相关的。STBC3r=3/4,1,STBC3r=3/4,2,STBC3r=3/8,STBC4的推导过程同理可得,本文不再推导。

自相关CNN算法对输入信号进行预处理的方式是将I/Q采样信号进行自相关处理,再经过FFT后输入到CNN进行特征提取识别。

4.2 性能测试与分析

本节对文中自相关CNN算法进行仿真实验,SNR范围为-10～10 dB,每个SNR下进行1 000次蒙特卡罗仿真,仿真条件见第3.2节。

仿真 1算法性能分析

自相关CNN算法性能分析如图4所示,6种STBC编码类型信号随SNR变化的识别概率,直接对数据集进行FFT处理的CNN算法在SNR=0 dB时,算法的识别概率稳定在85%左右。而改进后的自相关函数预处理方法识别效果较好,在4 dB时,算法的识别概率能达到96%。

图5(a)～图5(e)依次为算法在-10 dB、-5 dB、0 dB、5 dB、10 dB的识别混淆矩阵,反映了6种STBC的识别情况。

从图5可以看出,自相关CNN算法的识别性能明显提升,尤其是对CNN算法中识别效果不佳的SM和AL两种编码的识别概率显著提高,在SNR=5 dB时,两种编码的识别概率为95%左右。

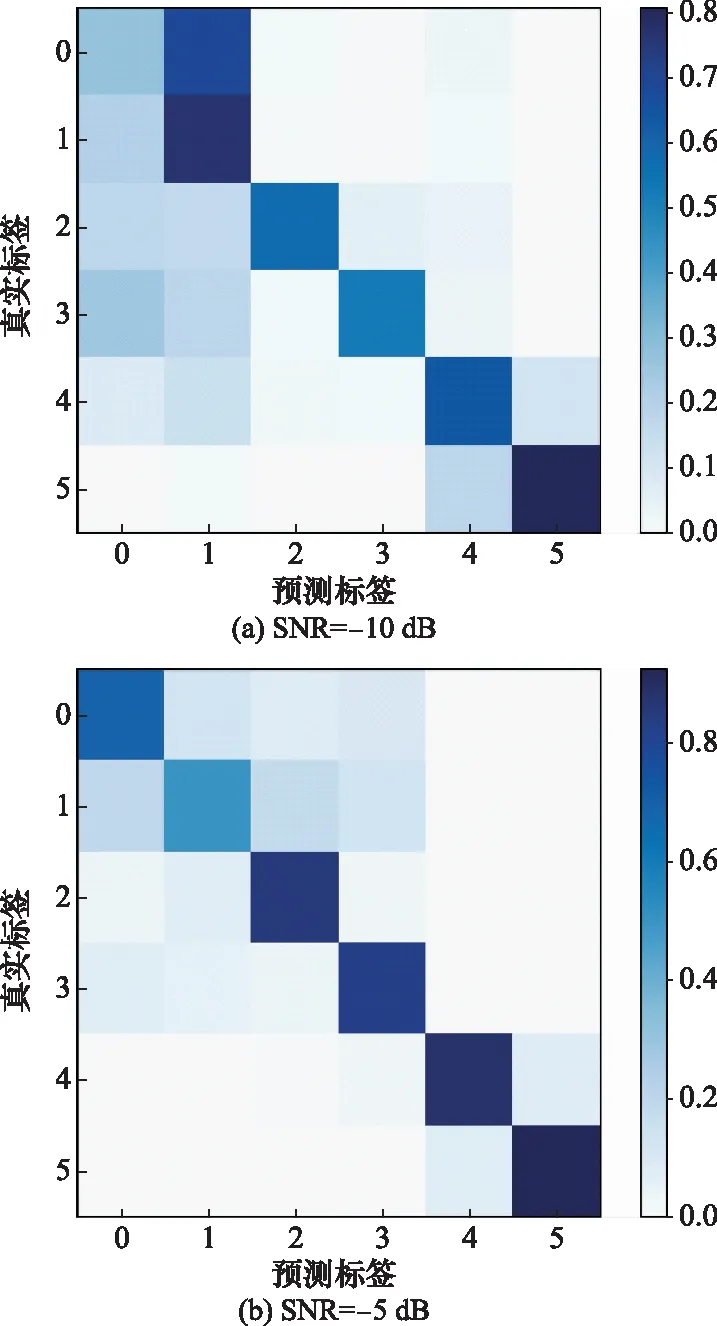
图5 自相关CNN算法在不同SNR下的识别混淆矩阵

仿真 2Nakagami信道m值对算法的影响

Nakagami信道m值对算法识别性能的影响如图6所示。观察可得,随着m值的减少算法的性能有所减弱,但对算法的识别性能影响不大。

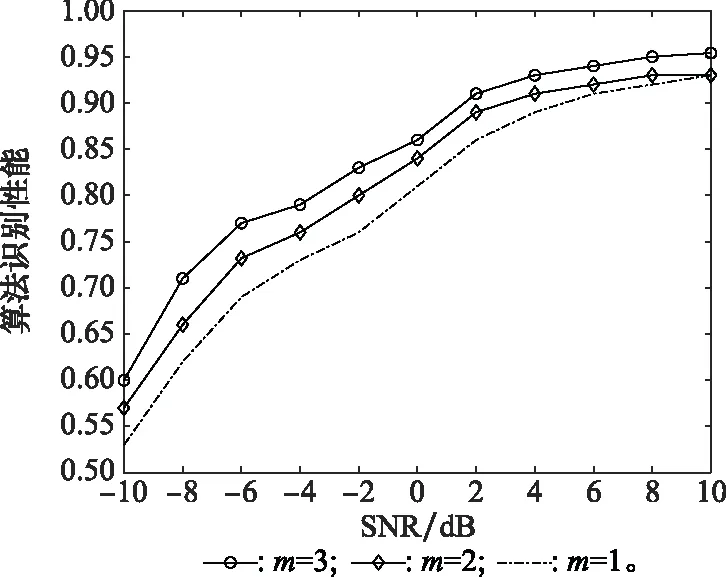
图6 Nakagami信道m值对算法的影响

仿真 3调制方式对算法的影响

调制方式与算法性能的关系如图7所示,采用BPSK、QPSK、8PSK、16QAM等4种常见的调制方式进行分析。

由图7观察可得,算法在BPSK下性能最好,识别率可以达到97%；QPSK的识别率最高为95%；8PSK的识别率有所下降,可以达到89%；而在16QAM时识别性能恶化,最高识别率仅为79%左右。

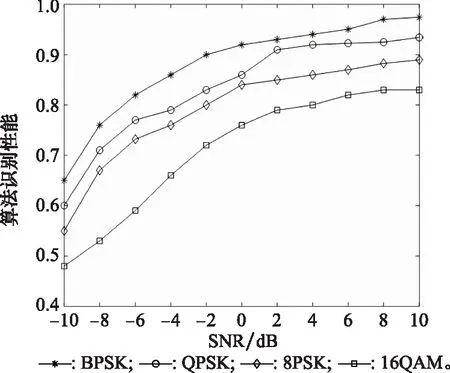
图7 调制方式对算法的影响

仿真 4采样点数N对算法的影响

采样点数N与算法性能的关系如图8所示。观察可知,采样点数N为128和64时,识别效果良好,相差不大。但当N为32时,算法的识别性能较差。这是由于采样点数N的增加可以提高频率分辨率,从而提升算法性能,但当N取值偏小时,识别数据量太小导致算法的识别性能不佳。

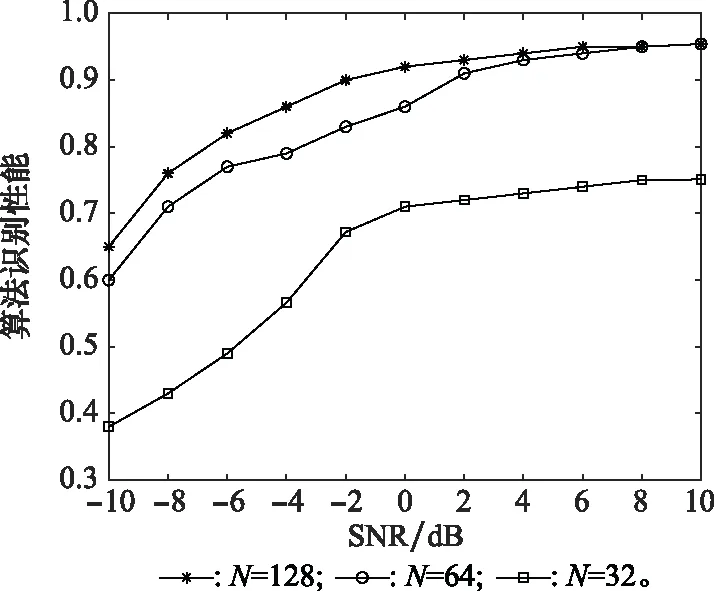
图8 采样点数N对算法的影响

4.3 网络训练分析

本文提出的CNN算法和自相关CNN算法网络在数据集下的训练与测试损失函数如图9所示。

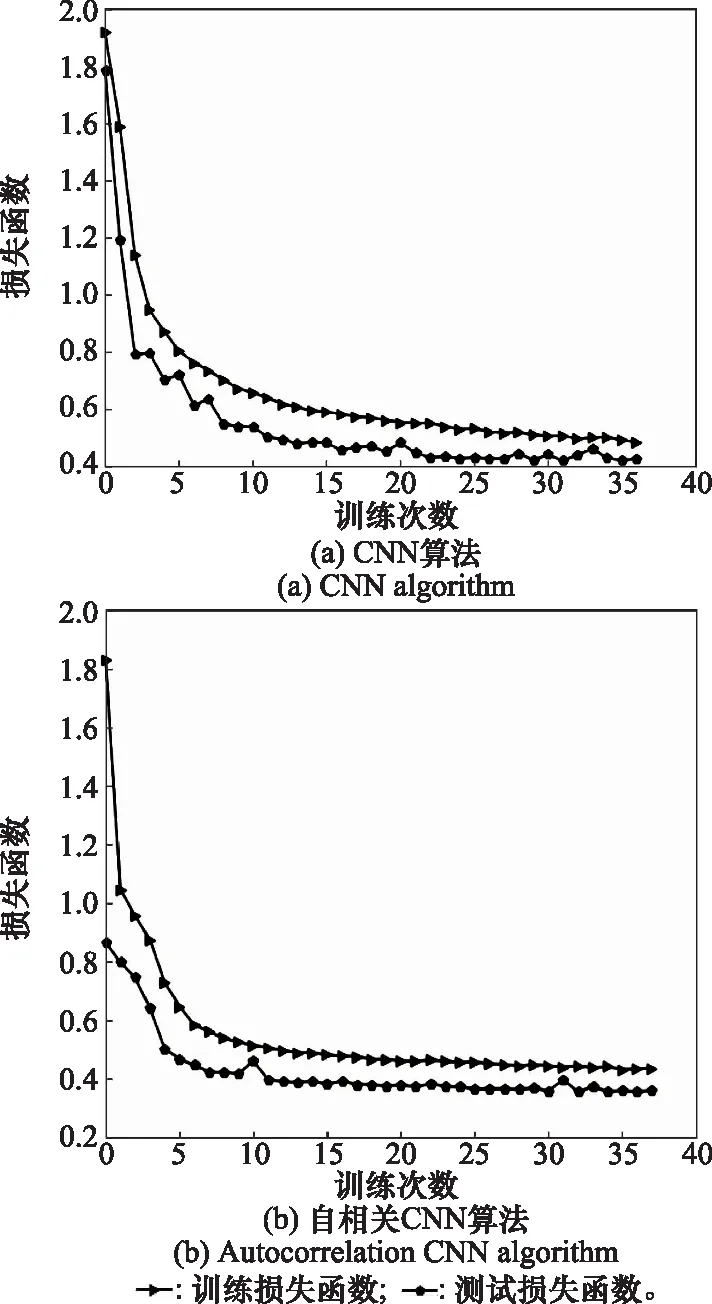
图9 训练次数与损失函数图

从图9中可以看出,CNN算法经过大约15次训练,网络的损失函数趋于稳定,没有出现明显的波动。说明本论文提出的CNN训练过程良好,收敛速度快,未出现过拟合或欠拟合的问题。而自相关CNN算法经过大约10次训练,网络的损失函数趋于稳定,收敛速度有所提升。

4.4 与传统基于特征识别算法比较

4种STBC算法的识别率和本文CNN算法及自相关CNN算法的比较如图10所示。CNN算法在低SNR下识别效果较差,主要是由于AL和SM的识别率低的不良影响。

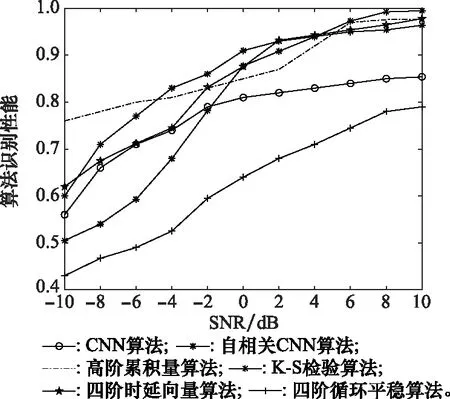
图10 算法性能比较

HOC算法、四阶时延向量算法、KS检验算法在SNR≈6 dB时,识别概率均能达到98%,而四阶循环平稳算法由于在该仿真条件下样本数量少,统计特性不明显,因此识别效果较差。

实时性分析如下:

从实际运行结果来看,自相关CNN算法训练速度约为3 s/epoch,每次识别耗时总长约为130 s,基本满足实时应用需求。

CNN算法和自相关CNN算法在5 dB时识别概率约为95%左右,识别性能比传统基于特征识别的算法要稍低一些,主要是由于CNN算法和自相关CNN算法能够对6种STBC码进行识别,尤其是可对于3种相似度高的STBC3码以及STBC4码进行识别,影响了其识别性能。CNN算法和自相关CNN算法通过建立CNN网络进行编码分类识别,减少了传统算法中人工设计特征值中存在的不足。

5 结 论

本文结合深度学习的优势,利用CNN提出了一种基于CNN多STBC编码类型的盲识别的算法,是首次在频域上使用CNN实现编码类型识别的算法,与时域上的算法相比,不需要接收端同步,大大提高了算法的适用性。仿真实验验证,基于CNN算法能够识别6种STBC编码,将目前能够识别的STBC编码类型从4种扩充到6种,尤其是能够识别3种相似度高的STBC3码,但本算法存在对AL码和SM识别概率较低的问题。针对AL和SM识别概率低的问题,将所提的CNN算法进行改进,对接收信号进行了自相关函数预处理,以提高CNN的特征提取能力,自相关CNN算法能有效对6种STBC编码类型进行识别,在4 dB时,识别概率能达到96%。

本文模型在识别过程中不需要利用大量样本数据得出相关参数,且复杂度较低,大大节省了识别时间,具有较好的工程应用价值。