面向系统性能最大化的装备经费结构SD优化
2021-04-07陈国卫周雨菁
陈国卫, 周雨菁, 任 蕾
(海军工程大学管理工程与装备经济系, 湖北 武汉 430033)
0 引 言
武器装备的发展受到很多条件的限制,其中最为关键的就是经费资源的约束[1-2]。优化与控制装备经费的结构尤其重要,这是解决较长一段时间内,装备经费供求紧张这一矛盾的根本办法[3-5]。系统动力学(system dynamics,SD)方法擅长把研究对象看成一个系统,强调从系统的结构入手,认为系统的行为模式与特性主要植根于其内部的动态结构和反馈机制,即遵从“结构决定行为”这一系统科学原理[6-9],这种按照系统论、基于对系统内部结构的透彻掌握而开展的分析,由于数据获取的层次较低、易于获取相对真实的费用数据,也由于通过系统的建模,能够正确地表达各费用及费用影响因素之间的相互关系,因而其结论相对而言更为可靠,在装备经费结构优化的研究中发挥了较好的作用。
魏汝祥等[10]采用SD方法绘制了装备维修费结构的因果关系图,给出了建立装备维修费结构动态分析方程式的程序,对装备维修费结构优化进行了理论分析。罗飞[11]、张栋[12]和张守玉等[13]采用SD方法建立了装备全寿命费用控制模型,通过数值仿真计算出了实现目标效能的时长,实现目标效能时需要多少经费,科研费、采购费、维修费等的总量分别为多少以及相互之间的比例。张怀强等利用SD方法分析了影响装备“三费”(科研费、购置费和维修费)比例的因素,并用因果关系图分析了“三费”与其影响因素之间相互影响的反馈机制和内在规律[14],建立了一种基于SD的装备经费结构优化模型[15]。陈国卫等[16-17]结合装备经费结构的层次性特点,从外部和内部两个方面分析了影响装备经费结构的主要因素,在此基础上建立了全寿命角度装备经费结构的因果关系图和各军兵种之间装备经费结构的因果关系图,提出采用SD方法和Vensim软件对装备经费结构进行动态分析,并给出了进行动态分析的主要步骤[18]。文献[19]提炼了武器装备系统寿命周期的6个阶段,总结了寿命周期4类系统费用,依据费用分解结构原理,建立了武器装备系统寿命周期费用分解图,构建了武器装备系统寿命周期费用优化模型,对寿命周期费用效能优化具有重要意义。此外,姜晓峰等[20]利用装备边际性能递减规律,分析了基于技术构成的装备经费结构优化。张涛等[21]运用微观经济学中的生产理论,通过静态和动态两个角度分析武器装备经费支出结构,最后从战略确认、增量优化与存量调整相结合以及加强武器装备经费运行管理等方面给出了战略驱动下的武器装备经费支出结构优化的对策。张怀强等[22]还分析了不同时期国家战略部署、科研发展情况及经济承受能力对装备经费分配的影响,基于博弈的方法,构建了装备科研费、购置费和维修费之间的比例关系优化模型。
综上所述,分析发现,关于装备经费结构优化的研究成果主要集中于寿命周期各阶段经费的分配和军兵种之间经费的分配,而围绕装备系统组成单元之间的费用分配问题、实现装备最优性能经费分配等方面的研究相对较少。比如装备的研制经费直接与装备战术技术性能指标的高低相关,对于既定的经费实施科学合理的分配,可以消除制约总体战术技术性能的短板,也可以避免对于总体战术技术性能无效的“长板”,因而对于提升装备经费的使用效益具有重要意义。
只要是在有限的费用条件下,在相互影响和制约的系统组成部分之间分配费用,就存在费用竞争和最优经费分配问题。包括在一个系统的各组成单元之间分配经费,在一个单元的多个指标之间分配经费,甚至在一个系统的各组成单元的多个性能指标之间分配经费等。文献[23]利用SD方法具有多领域的强大建模能力的特点,将系统热力学模型和系统优化计算模型融合在一起,初步对面向系统性能最大化的装备经费结构优化进行了分析,建立了面向系统性能最大化的动力系统费用结构优化因果关系图,初步分析了该费用结构优化系统内部的各种关系和反馈回路。该方法与用于军兵种经费结构等传统费用结构的分析研究方法之间最大不同之处是,系统与设备间不仅存在费用关系,还存在热力学模型的约束关系。对于某一装备系统,以系统总体的作战使用能力最大为目标,确定特定费用在该装备系统的各个组成设备之间的分配比例,即为该系统在设备层面的费用最优结构,这也是装备经费结构优化的主要内容之一[3,24-25]。
1 相关假设
一是假设某一简化的汽力装置,由两台锅炉、一台主机、一个给水泵和一个冷凝器组成[23]。由于对系统的推进功率尚不满意,因而决定再投入一笔经费对系统进行改进,优化的目标是在既定的经费下实现动力系统的推进功率最大化。
二是为了简化计算,假设主机功率仅取决于动力系统的锅炉、主机、给水泵、冷凝器等设备的性能。其中,锅炉的性能包括锅炉蒸发量、过热蒸汽压力和过热蒸汽温度;主机的性能包括最大功率和有效效率;给水泵的性能包括排量、扬程和效率;冷凝器的性能主要是冷凝器压力。
2 研究思路
众所周知,设备的一些性能是由研制和制造而产生、决定的。因此可以认为,对设备增加费用投入,就可以对设备进行改进,使设备的性能得到某一程度的提高,而由这些设备组成的系统的功率或效能也会有所提高。以上文假设确定的动力系统为例,对该动力系统增加费用投入,对系统进行改进,提高该系统的运行功率。这是因为,随着费用投入的增加,锅炉、主机、给水泵和冷凝器的各个性能就会得到某一程度的提高,从而使主机功率也得到提高,也即使动力系统的运行功率得到提高。但是,由于各个设备的性能对主机功率的影响不尽相同,而且有的性能与性能之间还存在一定的相互作用和相互影响,即系统运行时,性能之间必须相互匹配,所以在费用投入之时,应考虑该费用在各性能之间、各设备之间的投入比例,使有限的费用投入产生最大的系统功率增量。本文将在文献[23]的基础上,继续分析费用在各设备之间的投入比例问题,即对于一笔费用,以动力系统的功率最大为目标,确定该笔费用在锅炉、主机、给水泵和冷凝器之间的投入比例,也就是该笔费用分配的最优结构。
3 装备经费结构SD优化仿真模型构建
3.1 系统流程图
在文献[23]的基础上,依据SD原理和动力系统运行的基本原理[26],得到如图1所示的面向系统性能最大化的动力系统费用结构优化系统流程图。系统流程图一般由状态变量、速率变量、辅助变量、常量等要素组成[27]。在图1中,一共有13个状态变量、13个速率变量、13个辅助变量和11个常量,如表1所示。
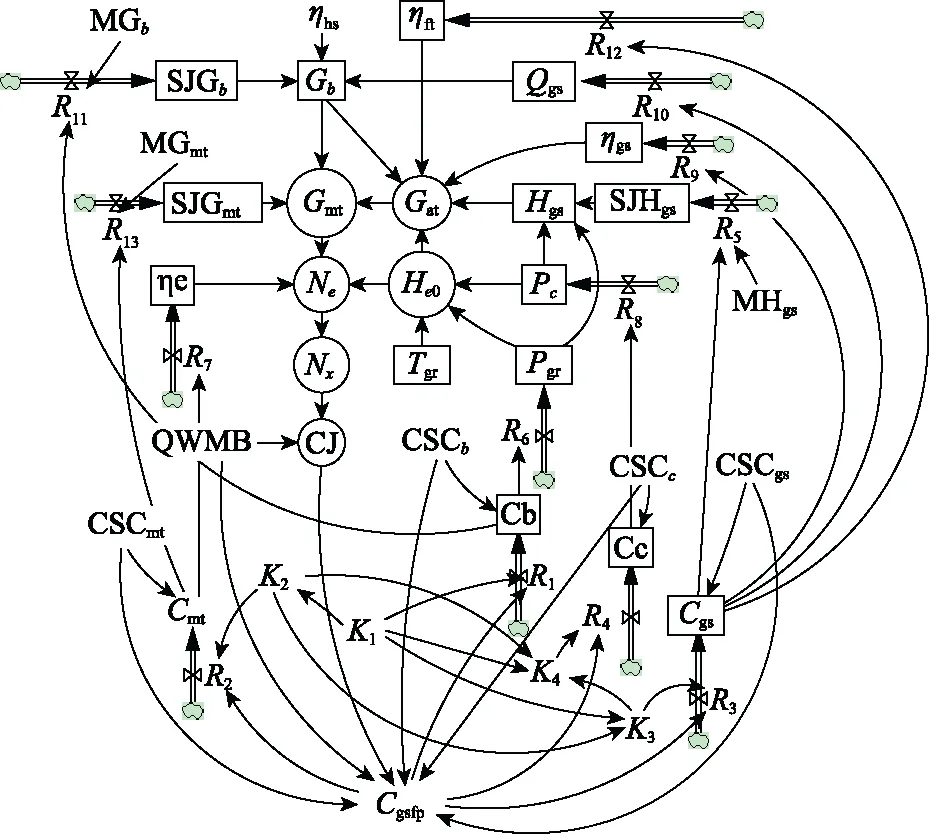
图1 面向性能最大化的动力系统费用结构优化系统流程图
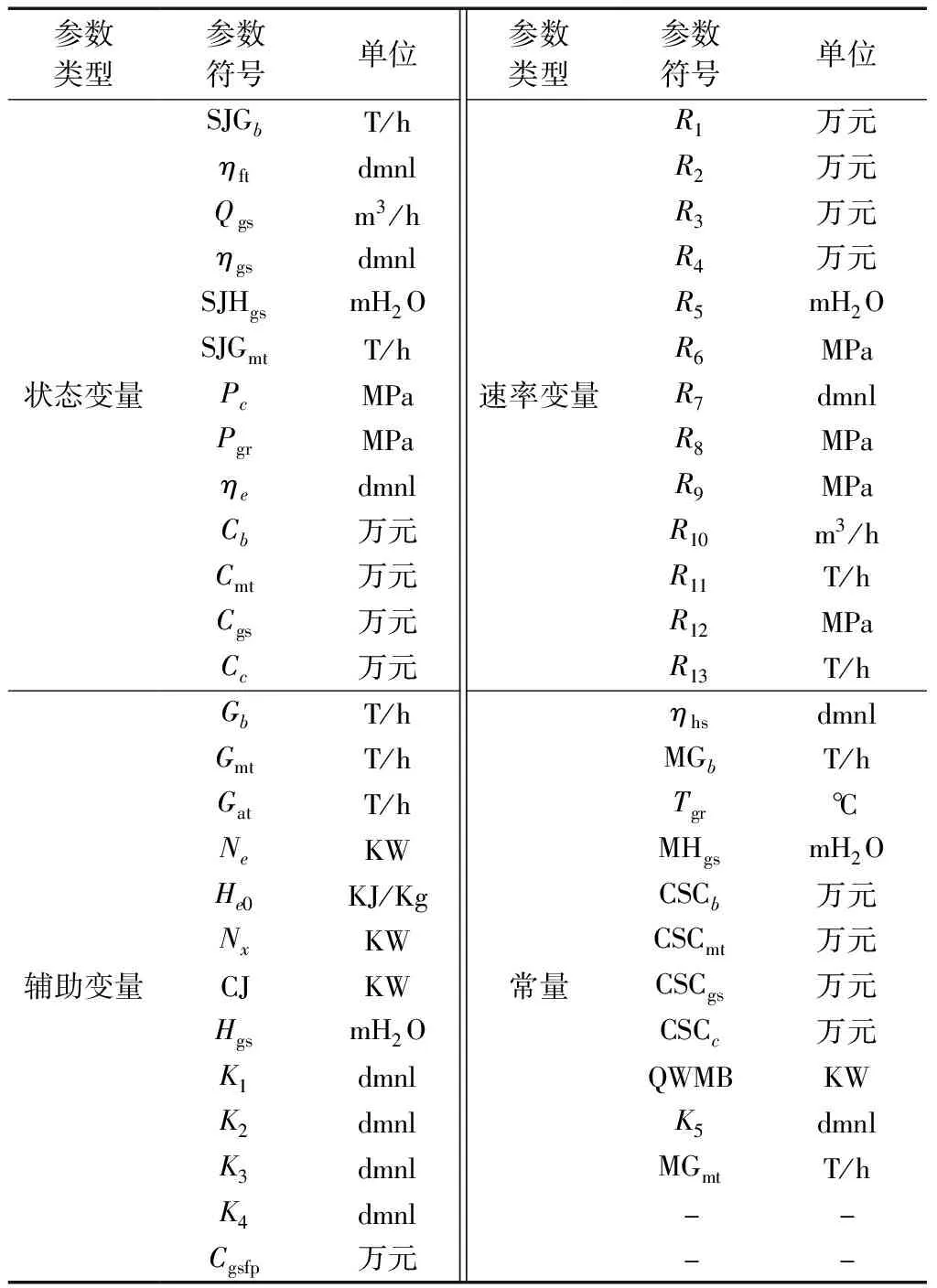
表1 面向性能最大化的动力系统费用结构优化模型参数
3.2 系统模型
根据图1中各种参数的关系、动力系统运行的基本原理以及SD的基本原理,构造面向系统性能最大化的动力系统费用结构优化的模型方程式为
Ne=GmtHe 0ηe
(1)
式中,Ne为主机功率;Gmt为主机耗汽量;He0为绝热焓降;ηe为主机效率。
Gmt=IF THEN ELSE
(Gb-Gat≤SJGmt,Gb-Gat,SJGmt)
(2)
式中,Gb为锅炉蒸发量;Gat为辅机耗汽量;SJGmt为设计产生的主机耗汽量。
SJGmt=INTEG(R13,0)
(3)
式中,R13为设计主机耗汽量变化速率。
R13=MGmt(1-e-Cmt)
(4)
式中,MGmt为主机极限耗汽量。
He0=f(Pgr,Tgr,Pc)
(5)
式中,Pgr为过热蒸汽压力;Tgr为过热蒸汽温度;Pc为冷凝器压力。由于本文研究所使用的SD仿真软件的建模解算能力有限,只能假设过热蒸汽温度随过热蒸汽压力线性变化,并同时假定终焓不变,使绝热焓降变为过热蒸汽压力的单一函数。由此并根据水及水蒸汽热力性质函数[28],对式(5)进行数值拟合,He0可进一步表示为
(6)
(7)
式中,Hgs为扬程;ηgs为给水泵效率;ηft为辅汽轮机效率。
Hgs=IF THEN ELSE
(Pgr-Pc≤SJHgs,Pgr-Pc,SJHgs)
(8)
式中,SJHgs为设计产生的扬程。
SJHgs=INTEG(R5,0)
(9)
式中,R5为设计扬程变化速率。
R5=MHgs(1-e-Cgs)
(10)
式中,MHgs为极限扬程。
ηft=INTEG(R12,α)
(11)
式中,R12为辅汽轮机效率变化速率;α为初始辅汽轮机效率。
(12)
Gb=IF THEN ELSE
(Qgs/Hhs≤SJGb,Qgs/Hhs,SJGb)
(13)
式中,Qgs为排量;Hhs为回水率;SJGb为设计产生的锅炉蒸发量。
SJGb=INTEG(R11,0)
(14)
式中,R11为锅炉设计蒸发量变化速率。
R11=MGb(1-e-Cb)
(15)
式中,MGb为锅炉的极限蒸发量。
Qgs=INTEG(R10,β)
(16)
式中,R10为排量变化速率;β为初始排量。
(17)
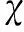
(18)
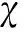
(19)
Pc=INTEG(R8,δ)
(20)
式中,R8为冷凝器压力变化速率;δ为初始冷凝器压力。
(21)
ηc=INTEG(R7,ε)
(22)
式中,R7为主机效率变化速率;ε为初始主机效率。
(23)
Tgr=INTEG(R6,φ)
(24)
式中,R6为过热蒸汽压力变化速率;φ为初始过热蒸汽压力。
(25)
式中,Cb为投给锅炉的费用。
Cb=INTEG(R1,CSCb)
(26)
式中,R1为投给锅炉费用的变化速率;CSCb为初始投给锅炉的费用。
R1=K1Cgsfp
(27)
式中,K1为改善费用分配时,投给锅炉的费用比例;Cgsfp为改善分配的费用。
(28)
R1~R13与费用之间的关系,是依据相应设备的研制费调研和统计结果,以及文献[29-30]中的数据进行拟合并经过脱秘处理而得到的。
CJ=QWMB-Nx
(29)
式中,CJ为差距;QWMB为期望目标;Nx为动力系统功率。
Nx=Ne
(30)
Cmt=INTEG(R2,CSCmt)
(31)
式中,Cmt为投给主机的费用;R2为投给主机费用的变化速率;CSCmt为初始投给主机的费用。
R2=K2Cgsfp
(32)
式中,K2为改善费用分配时,投给主机的费用比例。
(33)
Cgs=INTEG(R3,CSCgs)
(34)
式中,Cgs为投给给水泵的费用;R3为投给给水泵费用的变化速率;CSCgs为初始投给给水泵的费用。
R3=K3Cgsfp
(35)
式中,K3为改善费用分配时,投给给水泵的费用比例。
(36)
Cc=INTEG(R4,CSCc)
(37)
式中,Cc为投给冷凝器的费用;R4为投给冷凝器费用的变化速率;CSCc为初始投给冷凝器的费用。
R4=K4Cgsfp
(38)
式中,K4为改善费用分配时,投给冷凝器的费用比例。
(39)
K1=RANDOM UNIFORM
(0,1,{seed})-0.25
(40)
K2=(1-K1)RANDOM
UNIFORM(0,1,{seed})-0.25
(41)
K3=(1-K1-K2)RANDOM
UNIFORM(0,1,{seed})-0.25
(42)
K4=1-K1-K2-K3-0.25
(43)
式(40)~式(43)中,RANDOM UNIFORM({min}, {max}, {seed})为随机函数,该函数的作用是产生一个介于min值和max值之间的数值,这个数值是随机产生的,但是其分布依赖于种子的确定,这里取该函数默认的种子;每项最后均减去0.25,目的是使总费用保持不变。
Cgsfp=IF THEN ELSE[CJ≤0.1,0,
(44)
依据SD原理,设置本模型的反馈策略为:初始投入时,投给锅炉、主机、给水泵、冷凝器的费用相等,为总费用的1/4。设置动力系统费用结构优化模型反馈计算的控制器为“CJ”,如式(44)所示。
(1)当计算得到“CJ”大于0.1时,需要改善费用分配,继续缩小“CJ”。具体策略为:“CJ”引起改善费用分配,重新分配的费用Cgsfp可表示为
(45)
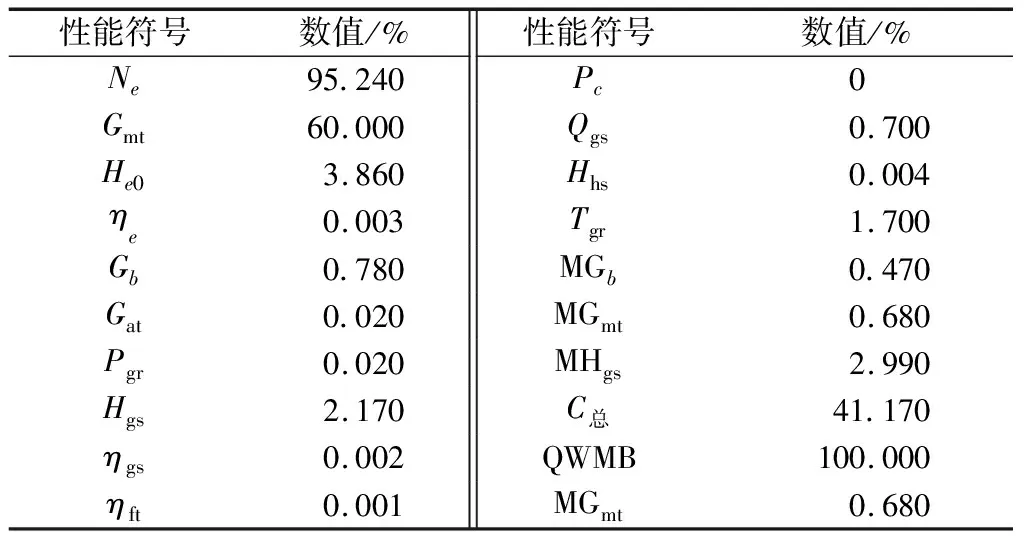
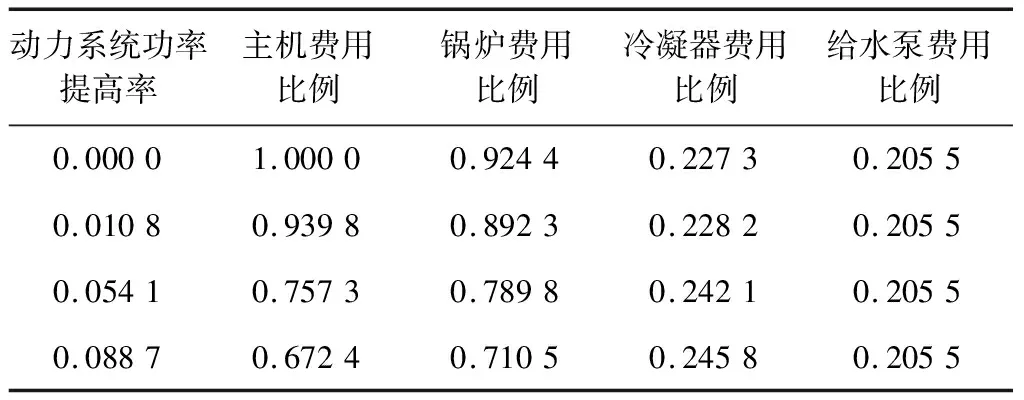
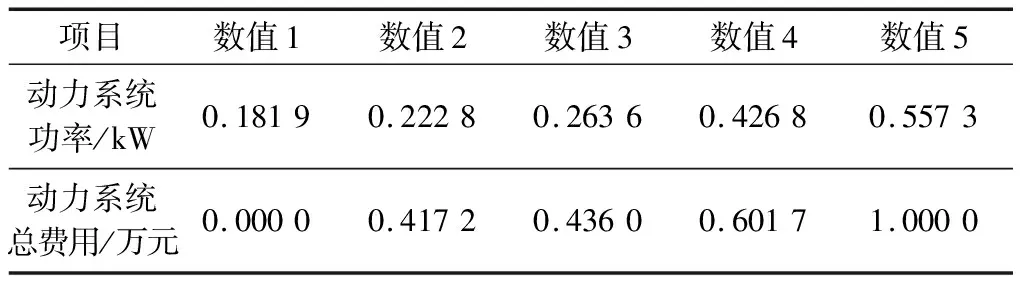
式中,CJ/QWMB为重新分配的费用占总费用的比例。0 (2)当计算得到“CJ”小于或等于0.1时,运算结束。 引用文献[31]中动力系统全工况运转时各性能参数的值作为本文动力系统正常运行时的性能初始值,并对数据进行归一化处理。这里采用0-1归一法,具体公式为 (46) 表2 性能参数初始值 仿真实验的主要目的是利用SD仿真模拟实际需求,根据模拟结果找到一些有价值的信息。在不同的仿真条件下,分析系统中状态变量和速率变量随时间的动态变化,研究系统参数确定条件下系统优化与稳定的时间,同时合理调整系统参数寻找系统变化规律,提出面向系统性能最大化的动力系统费用结构优化相应可行的政策建议。在表2初始性能参数的基础上进行仿真实验,在系统稳定时,得到仿真计算的数值结果,并根据式(46)进行归一化,可得表3~表6和图2~图5。 表3 动力系统功率对应的各个设备投入费用的增加量 表4 动力系统功率提高率对应的费用投入增加量在各个设备之间的分配比例 表5 动力系统功率对应的系统总费用 表6 动力系统功率提高的比例对应的设备费用投入增加的比例 图2 系统功率与设备费用投入增加量之间的关系 图3 系统功率提高率与费用投入增量在各设备之间的分配比例之间的关系 图4 系统功率与系统总费用之间的关系 图5 动力系统功率提高比例与各设备费用增加比例之间的关系 图2为动力系统功率与各设备投入费用的增加量之间的关系曲线,图3为系统功率提高率与费用投入增量在各设备之间的分配比例之间的关系曲线,表3为不同动力系统功率所对应的各设备投入费用的增加量,表4为动力系统功率提高率对应的费用投入增加量在各个设备之间的分配比例。 分析图2、图3、表3、表4可得:① 当系统的功率较小时,要提高系统功率,对应投入的各设备费用较少;而当系统功率达到一定程度后,再要提高相同比例的系统功率,对应投入的各设备费用就要大大增加,即要使系统功率稍微提高,就要投入大量的费用,如曲线在动力系统功率为0.85以后,上升趋势迅速增加;② 要提高系统功率,对应系统中各个设备的性能都要有所提高,即对系统中各个设备都要进行费用投入,且各个设备的性能要同时提高,性能提高以后,同时也要相互匹配,才能发挥出最大的系统功率;③ 当系统功率提高时,对应各设备投入的费用是不同的,这是因为不同的设备对费用的需求不同,即费用对设备性能的影响是不同的,有些设备要投入较多的费用,才能提升其性能,而有些设备性能提高所需要的费用较少;④ 当系统功率提高的比例不同时,对应的费用投入增加量在各个设备之间的分配比例也不同,这是因为不同的系统功率提高比例,对应的各设备性能的提高比例不同,设备各性能之间必须互相匹配,才能使性能得到完全利用,而不浪费多余的性能,使得系统的效能最大。 图4为动力系统功率与系统总费用之间的关系曲线,表5为动力系统功率所对应的系统总费用。 分析图4和表5可得:动力系统正常运转,产生预期的系统功率,则表明该系统已经达到标准设计要求,系统中各设备的性能也达到了标准。在此基础上,如果要通过提高设备的性能来提高系统功率,就需要投入较多的费用,如图4中动力系统功率0.2~0.25所对应的动力系统总费用,这是因为这一区间可能是该系统设计的瓶颈。在本例中,冷凝器压力的降低非常困难,是提高动力系统功率的一个瓶颈。如果突破了这一瓶颈,再要提高该系统的功率,只需投入相应的费用即可,如图4中动力系统功率0.25~0.50所对应的动力系统总费用。而到了系统功率的设计极限后,再要继续提高系统功率,就需要大量的费用投入,如图4中动力系统功率0.50之后所对应的动力系统总费用。 图5为动力系统功率提高比例与各设备费用增加比例之间的关系曲线,表6为动力系统功率提高的比例对应的设备费用投入增加的比例。 分析图5和表6可得:① 系统功率提高的比例越大,相应设备费用增加的比例也越大,这是因为系统功率提高越大,需要的费用越多,因此设备费用增加的比例也越大;② 系统功率提高的比例不同,对应的设备费用投入增加的比例不同,这是因为不同设备的性能对系统功率的影响也不相同,所以不同设备的性能提高的比例也不一样。 分析以上计算结果可知:① 如果要投入更多经费给动力系统中的各个设备,以提高系统功率,那么当该动力系统功率达到0.85时,此时投入的经费产生的效益最大,即该点为投入给主机、锅炉、冷凝器和给水泵费用的最优结构;② 如果总经费有限,那么当该系统的功率在0.25~0.50之间时,投入的总费用产生的效益就能趋于最大值,此后再投入的经费,产生的效益就会下降,导致投入总经费的效益也会下降;③ 如果要设计提高该系统的功率,应该考虑将费用重点投给冷凝器,因为降低冷凝器压力,是提高该系统功率的重难点。 使用文献[32-33]中的方法进行相对灵敏度分析。取锅炉蒸发量Gb为G(t),主机功率Ne为Y(t)。先对Y0(t)、Y1(t)、X0(t)和X1(t)进行式(46)的归一化处理;当X0(t)=0.022 5%时,Y0(t)=60.79%,然后对Ne进行灵敏度分析,分析结果如表7所示。可见,计算得到各参数的灵敏度都小于0.1,说明模型结构稳定性较好,仿真结果值得信赖。 表7 Ne的灵敏度分析结果 本文研究了设备的研制费用与设备性能之间的关系、设备的性能与动力系统的性能(推进功率)之间的关系,建立了各项费用与动力系统总体性能之间的关系模型,找到了费用在动力系统中各个设备之间分配的特殊规律,确定了功率既定情况下,动力系统费用的最小值以及在各个设备之间的最优分配结构。通过本文研究,在初步形成基于SD理论、面向系统性能最大化、在装备组成单元层面开展经费结构优化方法的同时,得到了许多有益的结论。 与其他装备经费结构优化与控制技术相比,一是本文采用的SD方法,充分利用了系统论的优势,强调从系统的结构入手开展分析,由于数据获取的层次较低,因而易于化解费用数据的获取难题;二是相比其他的装备经费结构优化研究工作,本文以蒸汽动力系统为例所开展的面向系统性能最大化的费用结构优化研究,更加直接地触及到费用结构优化的最低层,深层次地挖掘出了费用结构优化的原始起点,可以为更高层次的费用结构优化提供依据和参考。4 仿真实验与结果分析
4.1 仿真数据设置
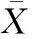
4.2 仿真结果分析

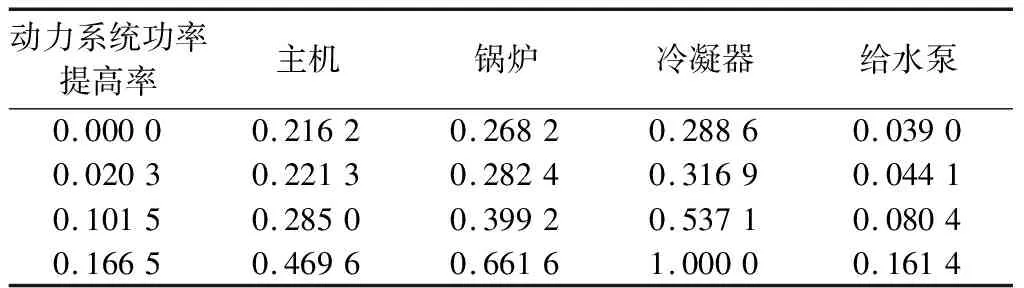
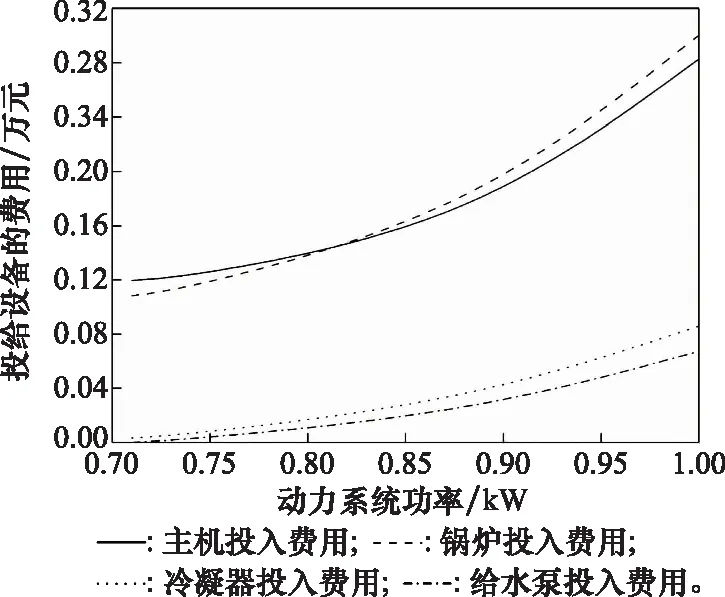
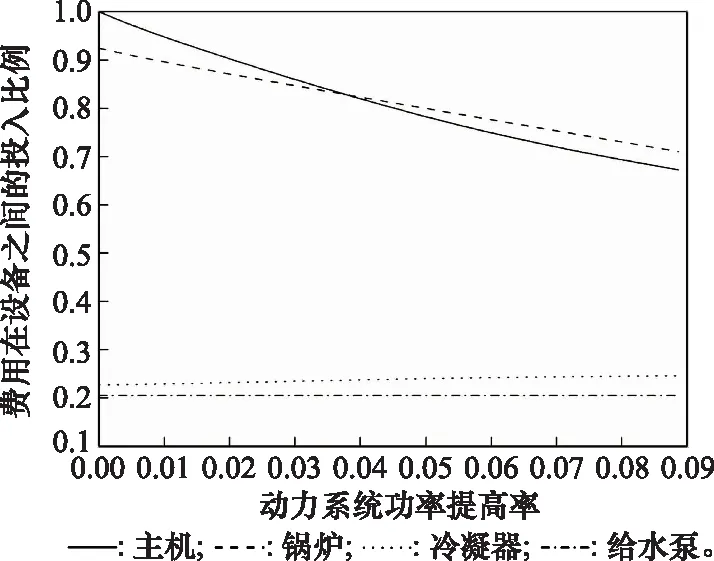
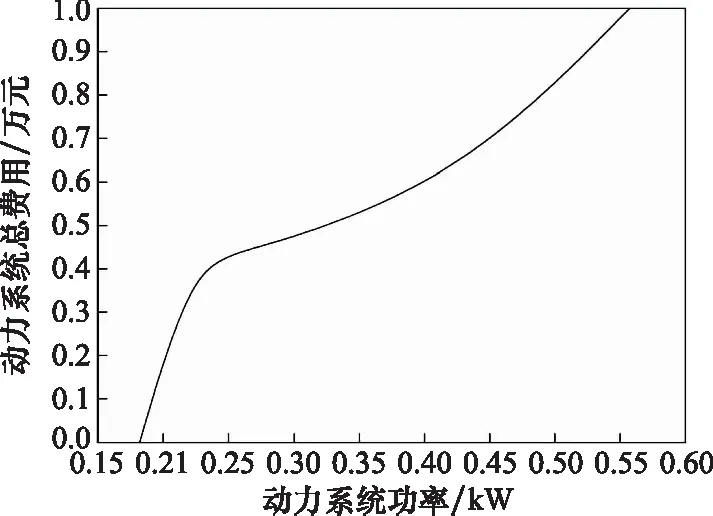

4.3 模型灵敏度分析

5 结 论
