改进差分进化算法求解武器目标分配问题

吴文海, 郭晓峰, 周思羽, 高 丽

(海军航空大学青岛校区航空仪电控制工程与指挥系, 山东 青岛 266041)

0 引 言

武器目标分配(weapon-target assignment, WTA)是指依据战术目标、武器性能、目标威胁等约束条件,结合实时战场态势信息,合理配置武器资源,确定最佳目标分配方案,以获得协同作战的最佳攻击效果,是典型的组合约束优化问题[1]。WTA作为协同作战中指挥决策的核心问题之一,吸引大量学者研究,具有重要的军事意义[2]。

WTA通常分为静态WTA(static WTA, SWTA)和动态WTA(dynamic WTA, DWTA)两类。SWTA将所有武器在单一阶段分配于目标;DWTA为多阶段决策问题,在不同阶段分配任务中,需考虑战场态势信息的变化,为后续决策提供依据[3]。WTA属于NP完全问题(non-deterministic polynomial complete, NPC)[4],求解WTA的计算量随维度增加呈指数增长,传统方法如目标规划[5]、博弈论框架[6]、启发式算法[7]、拉格朗日松弛法[8]等,能够实现对低维WTA问题求解,但难以对高维问题求解,全局寻优能力差,无法满足实际需求。智能算法以其寻优精度高、收敛速度快的特点被广泛应用于求解WTA问题。Zhou[9]等人提出一种离散粒子群优化算法,将遗传算法中均匀变异和交叉概念引入粒子群优化算法中求解SWTA问题;Sonuc[10]等人提出一种并行拟退火算法求解WTA问题;Chen[11]等人提出包括遗传算法和模因算法在内的进化决策算法求解DWTA问题;Li[12]等人将针对具体问题的种群初始化方法引入进化算法,改进选择操作机制,提高了求解SWTA问题的效率;Hu[13]等人提出基于精英策略的蚁群优化算法,改进路径选择、信息素更新等策略,对4种WTA模型进行求解。尽管上述方法在寻优精度方面有一定的改进,但收敛速度并不尽如人意,尤其面对高维问题,寻优精度和收敛速度仍有很大改进空间。

差分进化(differential evolution, DE)算法基于“贪婪竞争”的寻优策略,通过变异、交叉和选择操作实现种群进化,达到寻优目的[14],其控制参数少、寻优精度高、鲁棒性强、易于工程实现,被广泛应用于各领域优化问题[15]。近年来不少学者通过DE算法求解WTA问题,Deng[16]等人提出一种基于双种群的DE算法,分别采用浮点和序号对种群编码,进化过程中从浮点种群中生成相应的序列种群,实现求解SWTA问题;王少蕾[17]等人提出一种自适应DE算法求解WTA问题,利用混沌序列初始化种群,进化过程中变异、交叉因子随代数动态更新;Li[18]等人提出一种基于动态参数的变异策略,随DE算法进化过程推进,最优个体所占信息量不断增加。尽管上述方法对DE算法进行了改进,但进化过程中算法变异策略单一,个体邻域固定不变,静态邻域拓扑信息交换速率缓慢,无法平衡全局与局部搜索能力、减缓算法收敛速度,难以寻得全局最优;其次,进化过程中算法未能充分利用“精英”个体信息,寻优效率较低。

针对上述问题,为提高求解DWTA问题效率,本文提出一种基于随机邻域的自适应差分进化算法(random neighborhood adaptive differential algorithm, RNADE)。首先,RNADE为每一个体生成随机领域,领域中个体数量随进化过程动态更新,以平衡算法开发和探索能力。其次,引入基于历史进化信息的自适应参数策略,根据“精英”信息动态更新每代个体的变异因子和交叉因子。最后,基于小、中、大3种武器目标规模情境,与5种DE算法进行了18组对比实验。

1 DWTA问题描述

DWTA属于多阶段决策问题,其突出特点是在各阶段武器目标分配过程中,需实时考虑战场态势变化,适应动态求解环境,以获得全局最优攻击方案。“攻击-观察-攻击”是解决多阶段DWTA问题的常用策略,如图1所示。

图1 “攻击-观察-攻击”策略

“观察”指对战场态势进行分析,确定攻击目标及可用武器;“攻击”指求解武器与目标的分配结果,根据决策实施打击,“观察-攻击”的过程类似于SWTA问题[19],则DWTA可表示为

DWTA={SWTA(1),SWTA(2),…,SWTA(T)}

(1)

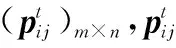
本文选取目标生存概率总期望值最小作为分配决策优化目标,则优化模型可表示为

minJ(X)=min{J(X(1)),J(X(2)),…,J(X(T))}

(2)

(3)

约束条件为

(4)

(5)

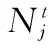
根据式(2)和式(3)可知,DWTA问题若想获得全局最优解,在每一阶段必须获得最优解,因此精确、高效地获得式(3)解是处理DWTA问题的关键。

2 改进差分进化算法

2.1 标准DE算法

DE算法是基于“贪婪竞争”的智能算法,通过变异、交叉、选择操作实现群进化。

(1)“DE/rand/1”

(6)

(2)“DE/best/1”

(7)

(8)

式中,Xmax和Xmin为搜索空间的上下界。

(9)

式中,jrand为控制参数；交叉因子CR∈(0,1)。

(10)

式中,f(·)为适应值。

2.2 随机邻域变异策略

本文提出一种基于随机邻域的变异策略,进化中为每代个体从当前种群随机挑选N个“邻居”,其中最优个体作为基向量,执行“DE/neighbor/1”操作,可表示为

(11)

式中,Xnbest为邻域中最优个体;Xr1,Xr2为除Xnbest外,邻域内随机挑选的个体。

邻域内个体数量N对DE搜索寻优能力具有重要的影响。N取较大值时,DE将具有较好的开发能力;相反,N取较小值时,DE将具有较好的探索能力。因此,合理地选择“邻居”数量N对平衡DE探索和开发能力,提高DE寻优性能起着重要的作用。本文提出一种自适应N值更新策略,随进化过程动态计算N值:

(12)

传统的DE仅采用固定的变异策略,减缓了算法收敛速度,甚至容易导致算法陷入局部最优[20],“DE/neighbor/1”策略充分利用邻域内“最优”和“随机”信息,加速信息交换速度,平衡全局探索和局部开发能力,避免在算法陷入局部最优的同时,提高种群多样性和算法收敛速度。

2.3 自适应参数策略

DE的控制参数对其寻优性能具有重要的影响,传统经验方法所确定的控制参数无法始终保持最优性[21]。因此,为了充分利用进化过程中的“精英”信息,本文采用基于历史进化信息存档的自适应参数更新策略[22]。

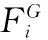
(13)

(14)

(16)

式中,meanWL(·)为权重莱默均值,可表示为

(17)

(18)

本策略充分利用“精英”信息保证控制参数最优性,同时采用柯西分布和正态分布提高随机性,保证种群多样性。

2.4 算法复杂度分析

3 基于RNADE的DWTA问题求解

3.1 DWTA问题决策流程

基于“攻击-观察-攻击”的DWTA决策流程如图2所示。

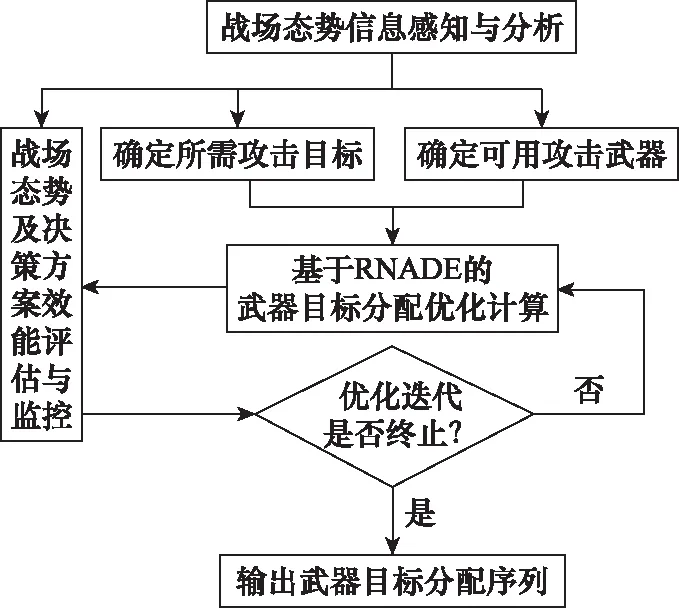
图2 DWAT问题决策流程

由图2可知,DWAT决策需根据战场态势分析结果确定当前阶段所需攻击目标及可用武器,将所确定的目标及武器输入RNADE执行优化迭代以获得武器目标分配决策,DWAT决策过程还需对分配结果及战场态势进行评估与监控,根据分配方案效果和战场态势信息,确定是否需要继续迭代求解。DWTA决策过程需动态更新所需攻击目标及可用武器,因此对算法寻优速度具有严苛要求,以满足武器目标分配决策的需求。

3.2 整数编码操作

WTA属于整数规划问题,编码方式需与其相适应,且满足对约束条件的表示。在m个可用武器和n个所需攻击目标情况下,每个个体Xi都是m维的整数,可表示为

Xi=(xi1,xi2,…,xim)

(19)

式中,xik∈[1,n],xik∈Z,xik为武器k所攻击的目标编号,具体编码操作如图3所示。

图3 整数编码

由图3可知,分配决策为

{W1T4,W2T1,W3T5,W4T2,W5T3,W6T1,W7T6}

则根据整数编码操作获得的个体向量为

X=[4,1,5,2,3,1,6]

3.3 RNADE流程框架

RNADE的伪代码如算法1所示。

算法1 RNADE的伪代码初始化:随机生成NP个体;设置k=1,MF和MCR中所有元素为0.5;while终止条件未达到do 重置SF=⌀,SCR=⌀; fori=1toNPdo根据式(13)和(14)生成FGi和CRGi;根据式(12)计算邻域个体数量NGi;为第i个体随机选择NGi个领域个体,选择最优个体为Xnbest;根据式(11)执行“DE/neighbor/1”生成变异个体VGi;根据式(9)执行交叉操作生成实验个体UGi;iff(UGi)H; endifendwhile输出:最优解x

RNADE的基本流程如图4所示。

图4 RNADE流程图

4 实验分析

4.1 实验参数设置

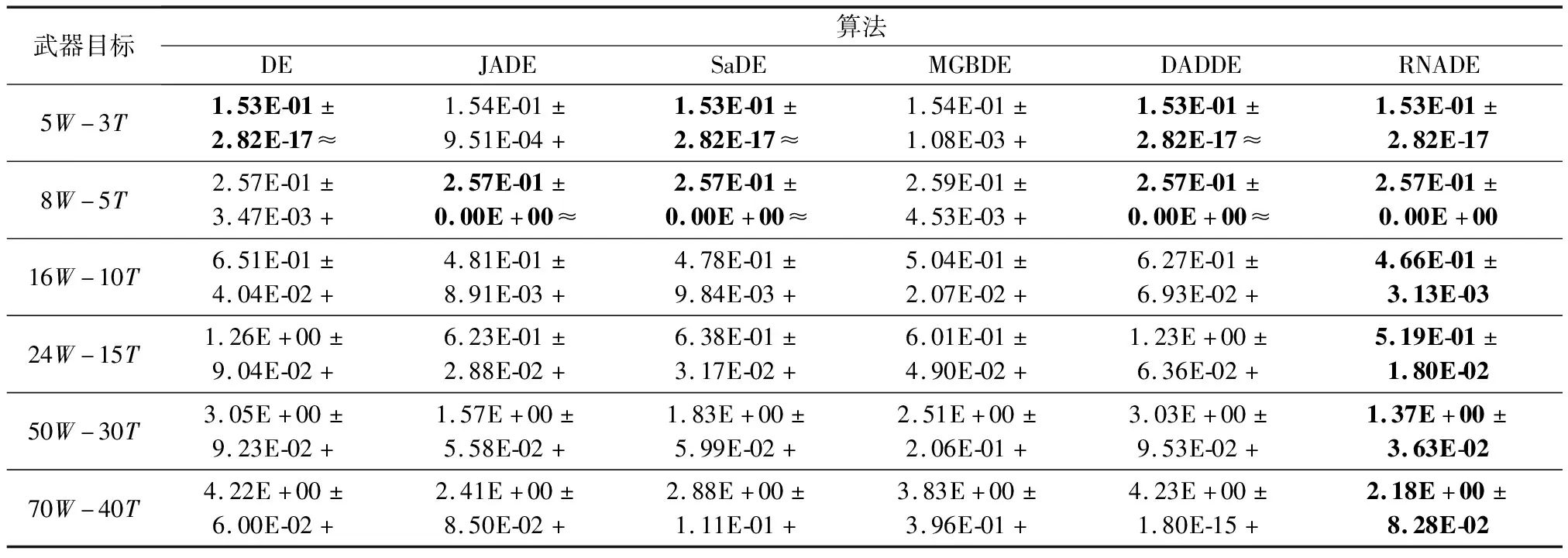
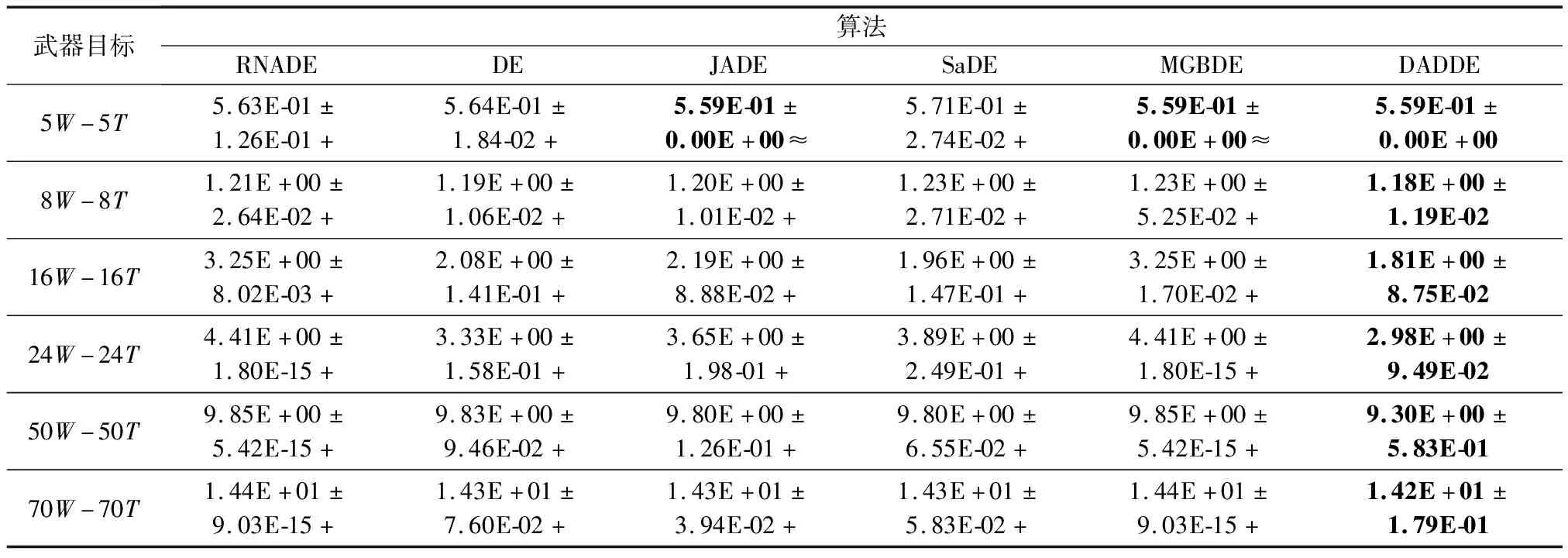
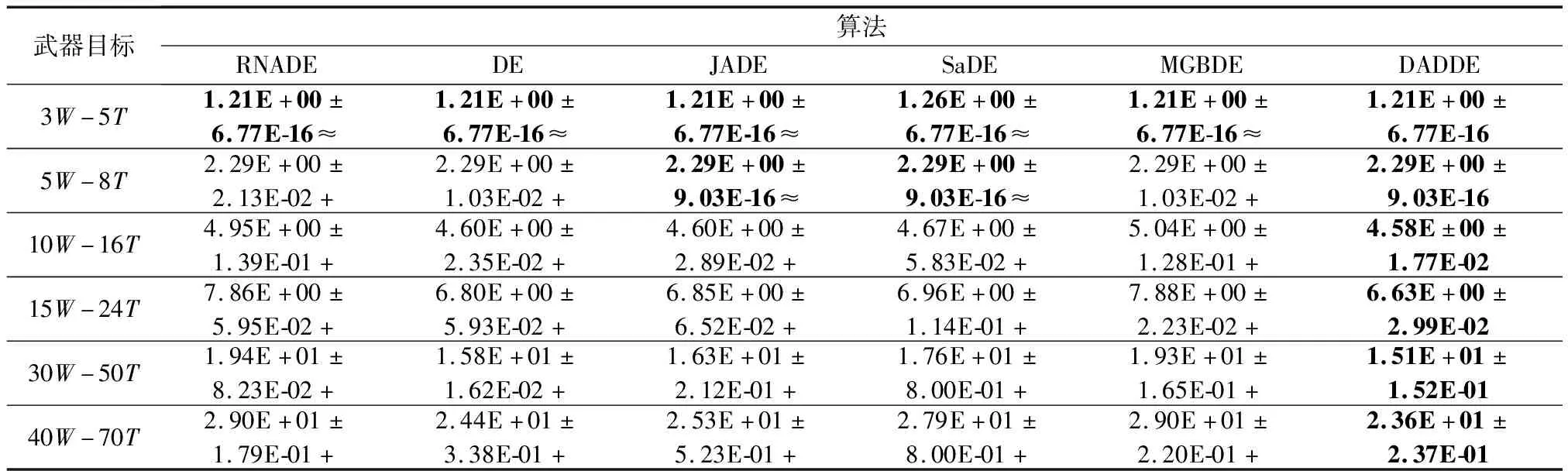
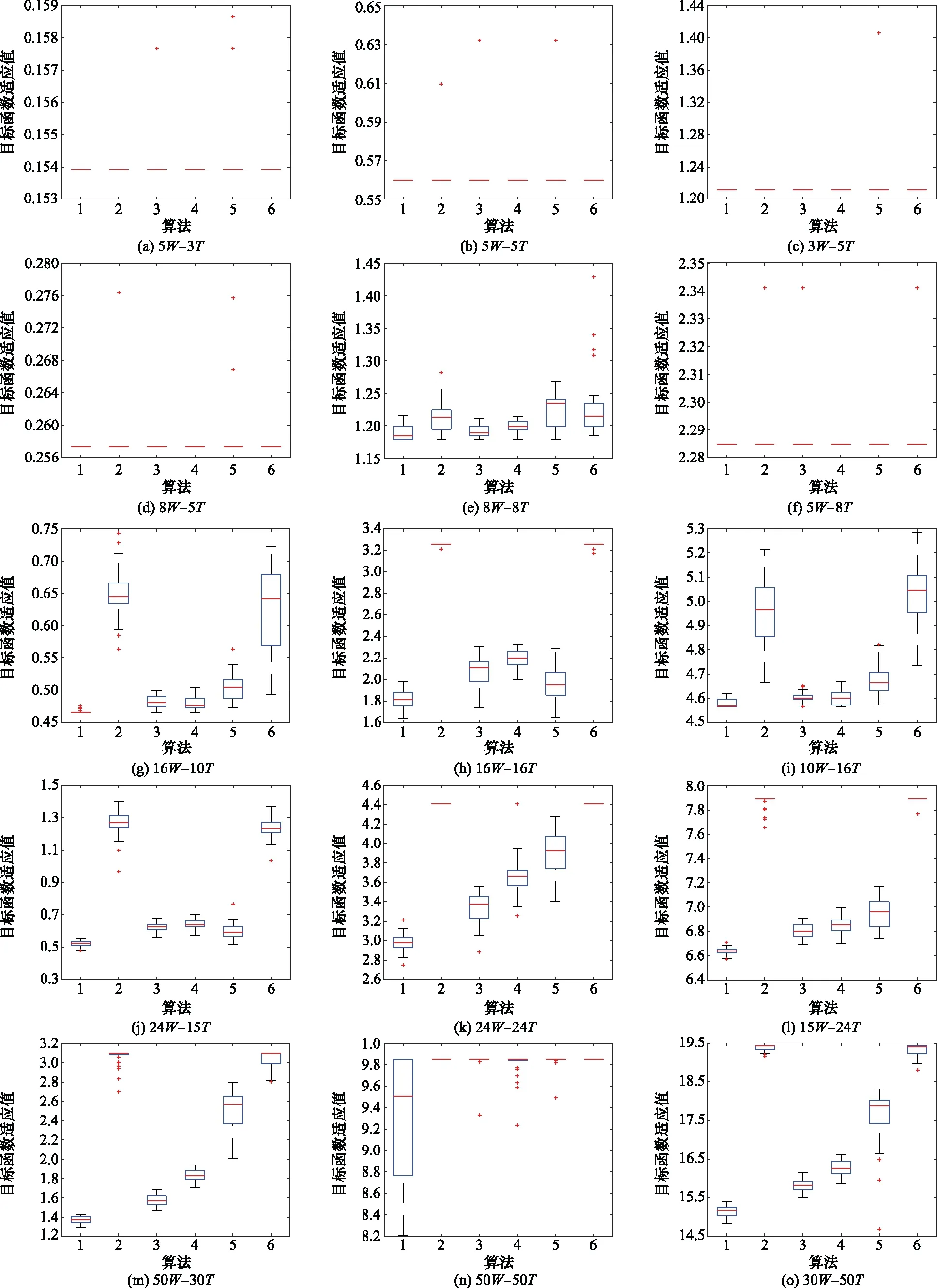
为了验证RNADE求解WTA问题的寻优性能,本文以空战为背景设置小、中、大3种规模的武器目标数量,其中武器数量可表示为战机携带导弹数量,目标可表示为敌机数量,则在小规模情况下可表示为单机或双机协同空战情境,中规模情况下可表示为具有4～6架战机的中队编队空战情境,大规模情况下可表示为“蜂群作战”模式下我方防空火力分配任务情境。实验分为武器数量大于目标数量(m>n)、武器数量等于目标数量(m=n)和武器数量小于目标数量(m

表1 测试分组设定

实验参数设置如下:武器i对目标j的毁伤概率pi j=0.4+ρ(0.95-0.4),目标j的威胁系数为vj=0.4+ρ(0.9-0.4);每组实验各算法独立运行30遍,最大函数评价次数max FES=2 000D,个体维度D=m。采用置信度为5%的威尔科克森秩和检验评估RNADE与其他算法之间显著性差异,“+/≈/-”分别表示RNADE优于/近似/劣于所对比算法。

4.2 RNADE与先进DE比较分析

为了验证RNADE处理DWAT问题的性能,将RNADE与标准DE[23]、JADE[24]、SaDE[25],MGBDE[26]以及DADDE[27]进行对比,各算法参数设置与原文献一致。

表2～表4分别为武器数量大于目标数量m>n、武器数量等于目标数量m=n及武器数量小于目标数量m

表2 实验结果(m>n)

表3 实验结果(m=n)

表4 实验结果(m

由表2～表4实验结果可知,RNADE在测试中寻优效果最好,18组测试中均获得最优值。根据威尔科克森秩和检验评估结果表明,标准DE、JADE、SaDE、MGBDE、DADDE分别仅有2、2、5、2、4组测试获得与RNADE近似的结果,其余测试结果均劣于RNADE。

分析表2～表4实验结果可以发现,5种算法获得与RNADE近似结果的测试均为小规模武器目标数量情况,中规模和大规模武器目标数量情况下5种算法寻优性能均明显劣于RNADE,尤其在大规模武器目标数量情况下;其次,相较于武器数量大于目标数量(m>n)和武器数量小于目标数量(m

为直观地评估RNADE寻优性能,图5给出了RNADE,标准DE、JADE、SaDE、MGBDE以及DADDE在18组测试中的收敛曲线。其中,横坐标FES表示为函数评价次数,即实验过程中调用式(3)对个体进行评价的次数,纵坐标为目标函数的适应值。

图5 各算法收敛曲线图

由图5可看出,RNADE的收敛曲线均快于其余5种算法,具有更快的寻优速度。尽管在小规模情况下其余5种算法的收敛速度并未明显劣于RNADE,但中规模及大规模情况下差距明显,如图5(h)、图5(l)、图5(n)、图5(q)。其次,从图5中可以看出,RNADE在武器数量等于目标数量m=n情况时,收敛速度远优于其余5种算法,武器目标规模越大,优势越明显。最后,图5还可以看出,除RNADE外其余5种算法均存在陷入局部最优,导致算法早熟现象,例如大规模武器数量等于目标数量(m=n)情况下。综合以上,说明RNADE出色的寻优速度和寻优精度。

采用取整操作会对算法处理小规模武器目标数量的WTA问题产生一定的影响,因为在武器目标数量较小的情况下,采取取整操作会使得原本寻优性能略差的算法在一定几率下也同样获得最优解。但是在中规模和大规模武器目标数量的WTA问题上,由于取整操作所带来的这种影响就变得非常小,根据表2～表4的结果和图5的收敛曲线可以看出,RNADE的寻优性能远优于其余算法,寻优精度和寻优速度均表现最好。这是因为随着维数的增加,武器与目标之间的分配方案急剧扩大,武器与目标之间的对应关系变得复杂,因此取整操作带来的影响将变的非常小,因取整操作而使得算法获得最优解的概率非常低。其次,在小规模武器目标情况下,我们依然可以看出RNADE收敛速度要优于其余算法,总体比较来看RNADE性能仍要胜于其余算法。

为了更直观地比较6种算法30次运行最优解的分布情况,分析各算法稳定性,图6给出了6种算法18组测试的盒图,算法1～算法6分别代表RNADE、标准DE、JADE、SaDE、MGBDE以及DADDE。

由图6可看出,在小规模武器目标数量情况下6种算法最优解分布情况集中,仅少数几组测试存在极端异常值情况,各算法稳定性相对较高;在中规模及大规模武器目标数量情况下,RNADE稳定性最好,尤其是在武器数量大于目标数量(m>n)和武器数量小于目标数量(m

图6 各算法盒图

仿真结果显示RNADE在30次实验中均收敛到相同的武器目标分配方案。由于中规模和大规模武器目标数量较大,在此仅列出小规模情况下寻优分配方案。

X5-3=(2,3,3,1,1)与之对应的分配决策为{W1T2,W2T3,W3T3,W4T1,W5T1};

X5-5=(2,1,3,4,5)与之对应的分配决策为{W1T2,W2T1,W3T3,W4T4,W5T5};

X3-5=(3,1,2)与之对应的分配决策为{W1T3,W2T1,W3T2};

X8-5=(2,3,2,4,1,4,3,5)与之对应的分配决策为{W1T2,W2T3,W3T2,W4T4,W5T1,W6T4,W7T3,W8T5};

X8-8=(5,8,4,2,3,6,1,7)与之对应的分配决策为{W1T5,W2T8,W3T4,W4T2,W3T1,W6T6,W7T1,W8T7};

X5-8=(4,8,1,3,5)与之对应的分配决策为{W1T4,W2T8,W3T1,W4T3,W5T5}。

采用弗里德曼测试进一步比较RNADE与其余5种算法处理WTA问题的性能。

基于弗里德曼测试的算法平均排序值结果如表5所示,黑体为最优值,由表5可知RNADE取得最优排序值,6种算法基于弗里德曼测试的排序为

表5 弗里德曼测试平均排序值

RNADEfJADEfSaDEfMGBDEfDADDEfDE

RNADE与5种算法的多重检验结果如表6所示,由表6可知,RNADE与DE、MGBDE、DADDE存在显著性差异。通过以上分析可知RNADE处理WTA问题的性能明显优于其余算法。

表6 多重检验结果

综合以上结果可知RNADE处理WTA问题具有良好的效果,寻优性能越明显优于其余算法。相较于RNADE,寻优性能存在显著性差异的3种算法:标准DE采用单一变异策略及固定控制参数,无法随进化过程进行动态调整,导致算法多样性不足,容易陷入局部最优,寻优性能差;DADDE虽采用2种变异策略,但策略本身缺乏动态更新能力,其次参数的整定采用确定性机制的自适应策略,进化过程中也未能充分利用“精英”信息,导致寻优效果较差;MGBDE改进变异策略,利用最优个体信息的同时采用高斯分布提高随机性,但MGBDE采用固定的控制参数,无法随进化过程调整种群的变异和交叉,导致寻优性能差。

RNADE能够充分利用进化过程中的“精英”信息提高算法的寻优精度,变异操作中以最优个体作为基向量,控制参数根据“精英”存档动态更新;同时能够保证算法随机性提高算法的动态性能,变异操作中为每一个体产生随机邻域,控制参数根据高斯分布和柯西分布动态更新。RNADE充分结合“最优性”和“随机性”,提高处理WTA问题的寻优精度和寻优速度。

5 结 论

为提高求解WTA问题的精度和速度,本文提出一种基于RNADE。采用“DE/neighbor/1”策略执行变异操作,为每一个体生成随机领域,领域中个体数量随进化动态更新,以平衡算法开发和探索能力;引入基于历史进化信息的自适应参数策略,根据“精英”信存档动态更新每代个体的变异因子和交叉因子。为验证RNADE求解DWTA问题的高效性,设置小、中、大3种武器目标规模,共18组测试,分别与标准DE、JADE、SaDE、MGBDE、DADDE进行比较。实验结果验证了RNADE求解DWTA问题的有效性,相较于对比算法,RNADE具有寻优精度高、收敛速度快、鲁棒性强的优点。