疫情背景下科创板股票指数的波动性研究

1 样本数据选取及股指体系构建

由于科创板刚刚在我国上市不久，还没有发布官方的股票指数，因此首先需要选取合适的样本构建股票指数。虽然科创板的股指还未发布，但已经确定出“科创50”指数对应的50家公司，此次样本就从这50家公司中挑选出10家最具有代表性的公司，主要考虑的指标有公司市值和股票的流动性，这也是参考“上证50”的指标进行选取的。此外，所选取的科创板公司还应考虑上市时间，此次优先考虑首批上市的公司，也就是在2019年7月22日上市的公司。结合以上指标，共遴选出以下10支股票：睿创微纳(688002)，乐鑫科技(688018)，心脉医疗(688016)，安集科技(688019)，南微医学(688029)，虹软科技(688088)，澜起科技(688008)，中国通号(688009)，中微公司(688012)，嘉园科技(688388)。此次选取的全时间轴样本区间为2019.07.23—2020.06.19，疫情期间样本区间为2019.12.02—2020.06.19。

采用加权综合法计算股票指数。将全时间轴的股票价格指数计算出来后，对股指序列进行平稳化处理，一般可以通过取对数或者做差分的方式使序列平稳，本文选用差分方法来消除序列的不平稳性。一阶差分后，得到序列DP：DP=P1-Pt-1。对序列进行ADF检验，其检验结果如表1所示。

表1 一阶差分后的ADF检验

对于表1中全时间轴的序列，在三个不同的临界值水平下，其ADF统计量的值小于临界值，且P值小于0.01，说明即使在99%的置信水平下，也可以拒绝存在单位根的原假设，因此序列是平稳的。同样，疫情期间数据在进行了一阶差分后的ADF检验结果也显示不存在单位根，即序列是平稳的，由此可以对这两个时间序列进行建模分析。

2 基于ARIMA-GARCH模型科创板股票市场的实证分析

2.1 ARMA-GARCH模型的估计和检验

2.1.1 ARIMA模型的估计及残差检验

将一阶差分后的股指序列做自相关和偏自相关检验，得到如图1所示的ACF和PACF图。

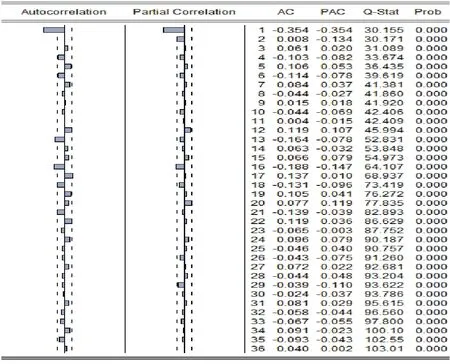
图1 一阶差分后的股指序列自相关检验图

从图1可以看到，P值都小于0.05，说明一阶差分后的股指序列为非白噪声序列。由ACF图和PACF图可以看到，p可能等于1、2，q可能等于1。因此分别建立ARIMA(1，1，1)和ARIMA(2，1，1)模型。ARIMA(1，1，1)模型AIC为6.437884，SC数值为6.487150，ARIMA(2，1，1)模型AIC数值为6.434243，SC数值为6.478274。根据AIC、SC准则，应当选取数值最小的模型，因此最终选择ARIMA(2，1，1)模型，模型的具体结果如表2所示。

表2 ARIMA(2，1，1)模型参数估计结果

从模型的结果来看，模型参数的P值均小于0.05，表明模型参数都显著不为0。模型的结果用公式表述为：

接下来对模型进行检验，首先，利用EViews模拟出残差的自相关检验图。从检验结果来看，其P值均大于0.05，表明残差序列为白噪声序列，即残差是纯随机性的，残差之间不存在相关性。

通过对残差的平方进行自相关性检验，检验结果显示，残差平方未通过自相关检验以及残差平方线型图显示不平稳，因此可能存在异方差现象，需要进一步的检验。

2.1.2 ARCH效应检验

通过上文的一系列分析，得出一阶差分后的股指序列可能存在异方差性，因此需要对其进行ARCH-LM检验，其检验结果如表3所示。

表3 ARIMA模型参数估计的ARCH-LM检验

从表3可以看出，统计量的P值均小于0.05，拒绝“残差序列不存在异方差性”的原假设，说明残差序列存在异方差性，即ARCH效应，需要进一步建立GARCH模型。

2.1.3 ARIMA-GARCH模型的估计及检验

本次研究选用GARCH(1，1)建立残差模型。利用ARIMA(2，1，1)-GARCH(1，1)模型对数据进行拟合，得到的结果如表4所示。

表4 ARIMA-GARCH模型的参数估计结果

可以看到模型估计的系数的P值均小于0.05，说明模型系数显著。根据表4中结果，其公式表述为：

建立好模型后，对模型再次进行ARCH-LM检验，观察其是否已经消除了异方差性。由检验结果得知统计量的P值均大于0.05，不拒绝“残差项不存在ARCH效应”的原假设，因此表明已经消除了ARCH效应，模型通过检验。

2.2 全时间轴与疫情期间股指模型的比较分析

疫情期间股指模型的估计及检验。将疫情期间的股指序列数据做与上文类似的处理：先通过一阶差分让序列平稳，接着通过其ACF图和PACF图判定p、q可能的阶数分别为0、1和1，因此分别建立ARIMA(1，1，1)模型和ARIMA(0，1，1)模型，并根据AIC和SC最小选择ARIMA(0，1，1)模型，模型结果如表5所示。

表5 疫情期间股指序列的ARIMA模型参数估计

由表5可以看出模型系数的P值小于0.05，通过检验。模型的公式表述如下：

接下来同样对其进行ARCH-LM检验，检验结果如表6所示。

表6 疫情期间股指序列的ARIMA模型参数估计的ARCH-LM检验

检验的统计量P值都大于0.05，因此不存在ARCH效应，不需要进一步建立GARCH模型。最终模型确定为ARIMA(0，1，1)。

3 结论与建议

3.1 主要研究结论

本文选取科创板中最具代表性的10支股票构成股票指数作为样本，并将其样本区间划分为疫情前和疫情期间，总的样本区间称为全时间轴，对全时间轴、疫情期间两个时间序列分别用EViews做分析，建立相应模型，并对序列的集群性找到主要原因，对比模型的预测效果，得到结论如下。

对于科创板的股票指数，在疫情前和疫情期间两个独立的时间区间内都是不存在异方差性的，但在整个时间轴区间内存在异方差性，说明疫情因素很有可能是引起异方差性的重要原因。

通过疫情期间和全时间轴模型的预测数据对比可知，虽然全时间轴模型消除了股指波动的异方差性，但其预测效果仍然不如疫情期间的数据模型。

GARCH模型对发达国家的成熟股票市场是一个良好且实用的模型，但对于我国这种新型股票市场，GARCH模型同样消除了股指序列的异方差性，也具有较好的实用性，并且可以结合ARIMA模型进行短期预测，预测效果比较可观。

3.2 相关建议

对于投资者而言，疫情期间由于各种不确定因素的存在，导致股票市场的波动相较于以往更为剧烈。但疫情期间在家又有更多的时间参与金融投资，因此在进行投资决策时，要考虑多方面的因素，可以结合股票的技术分析、构建模型进行股价预测等方法来制定投资策略。

对于相关政策的制定者而言，需要注意以下几点。

一是要加强信息公开。使投资者充分理解金融市场的各种情况，减少不理性操作，充分发挥市场的调节功能。

二是要完善风险管理制度。如建立涨跌到一定程度强制停止涨跌程度，大户进行持仓需要报告制度等以尽量规避风险。

三是要完善证券市场的法律法规。由于我国金融市场发展时间较短，许多的监管政策还不够完善，导致市场出现投机者通过市场监管漏洞进行获利进而伤害证券市场，因此完善证券市场的法制，才能减少市场投机者，规范市场交易。

四是要丰富我国金融衍生品。如上证50，沪深300等指数是丰富我国衍生品市场的巨大进步。金融衍生品可以完善我国金融市场体系，且具有稳定我国金融市场的作用，对于提高我国金融市场的竞争力有巨大帮助。投资者需要规避风险时，通过资产组合可以降低投资风险。所以，丰富我国金融衍生品对我国金融市场的发展有着重要意义。