基于改进Hough变换算法的圆形零件检测
2021-04-07熊保玉
熊保玉
(成都工业职业技术学院,四川 成都 610218)
圆形是零件最基本的特征之一,如果圆形零件检测效果较差,将影响设备的使用。如面包、沙琪玛等加工使用的圆形刀片精度决定了切割食品的质量,因此提高圆形零件检测精度具有重要意义[1]。
人工检测效率比较低,而且检测过程中不可靠因素较多,会影响产品质量与成本。接触式传感器检测一般是通过压电、电阻式传感器检测待加工圆形零件上的坐标实现,需要传感器与圆形零件接触,对圆形零件摆放位置具有严格的要求,灵活性差。非接触式传感器检测一般是通过电容传感器检测待加工圆形零件上的坐标实现,但是检测效果受传感器自身精度影响较大。随着现代信息技术的发展,视觉检测逐渐成为圆形零件检测中应用比较广泛的方法,卷积神经网络(Convolution neural network,CNN)用于零件检测[2],通过神经网络训练和卷积运算,能够降低运算的复杂度,但对小目标零件检测准确率并不是很高。Hough变换(Hough transform,HT)检测圆形零件时[3],通过机器视觉将圆上的点投影到参数空间,通过参数空间即可获得圆形零件特征,但是当参数空间为多维时,计算时间和空间将指数增加。随机Hough变换(Random hough transform,RHT),对圆形零件图像边缘点随机采样能够实现多对一变换[4],减少运行时间,但是如果圆形零件轮廓比较多,随机选取点的概率会降低。点Hough变换(Point hough transform,PHT)根据任意两条弦的中线在圆心处相交的理论[5],将计算空间降维,从而减少了计算复杂度,但检测精度不高。对称Hough变换(Symmetry hough transform,SHT)圆检测[6],利用圆的对称性以及累加半径投票得到圆的参数值,但是选取的半圆非常关键。
为了提高圆形零件检测的效果,试验拟采用改进Hough变换(Improved hough transform,IHT)算法,力图快速、准确检测圆形零件,为产品质量深入研究提供理论依据。
1 改进Hough变换圆形零件检测
1.1 基本Hough变换检测圆心与半径
将圆形零件图像空间的像素用解析形式联系起来,形成参数空间累积对应点[7-8]。假设圆形零件的方程表示为
(1)
式中:
x0、y0——圆心坐标;
r0——圆半径,cm。
圆形零件图像中任意像素点(xi,yi)都会在参数空间存在唯一的三维直立圆锥,计算为:
(a-xi)2+(b-yi)2=r2,
(2)
式中:
a、b——参数空间变量。
通过累积投票可以求得该点参数即为圆形零件的位置参数,圆形零件图像像素点集在参数空间形成三维圆锥面并且交于一点(a0,b0,r0),该点即为圆心位置。但是基本Hough变换存在如下缺陷:如果图像边缘点不清晰,将错误地找到圆形零件的圆心坐标和半径,导致检测误差较大;当圆形零件图像的边缘点较多时,使用基本Hough变换检测圆形零件的圆心坐标和半径计算量指数级增加,需要大量的处理时间。
1.2 改进Hough变换
1.2.1 基于最小误差的随机采样点计算 为了减少计算量,对圆形零件图像边缘像素点70%~80%抽样,减少无关的数据累加性[9-10]。设圆形零件图像直径端点边缘随机采样点为(x1,y1),同时限定直径取值范围为[Dmin,Dmax],圆形零件图像上直径相对于(x1,y1)的另外一个端点(x2,y2),在以点(x1,y1)为圆心,半径为[Dmin,Dmax]的圆环上:
(3)
从而获得圆形零件参数为:
(4)
对获得的圆形零件参数距离的平方和与半径的平方差计算为:
(5)
总随机采样点为n,则平均误差计算为:
(6)
标准误差计算为:
(7)
设置一个阈值:
(8)
式中:
k——系数。
对边缘随机采样点进行σi累计计算得到圆形零件参数数组,当结果中出现σi 1.2.2 虚假圆心排除 通过聚类算法避免虚假圆心的出现[11-12],如果存在两个候选圆X1和X2,圆心分别为(x1,y1)和(x2,y2),半径分别为r1和r2,假设有边缘点(x′,y′)满足: (9) 则视点(x′,y′)为候选圆上的点,统计候选圆上的边缘点的数量M,候选真圆阈值: Mmin=λ×2πr, (10) 式中: λ——比例系数; r——候选圆半径,cm。 若M>Mmin则当前候选圆为真圆,否则为假圆。λ可根据计算精度设定,λ越小,计算速度快但精度低,λ越大,计算速度慢但精度高,综合考虑,选取λ区间为[0.95,1.05]。 对候选圆的周围像素数量候选[13],并从中获得候选圆圆心及半径参数(x0、y0、r0),找出所有与该圆近似的候选圆形参数,将其放在同一类别中,以获得的各个圆的中心半径的平均值作为最终参数,公式如下: (11) 式中: xi、yi——圆心的横坐标、纵坐标; ri——半径,cm; n——划分类别中圆形参数的个数。 圆形度是限制实际圆对理想圆变动量的一项指标[14-15],属于圆形零件重要参数,实际圆形零件的圆形度计算为: (12) 式中: S——实际圆形零件像素区域面积,cm2; C——实际圆形零件像素区域周长,cm。 e∈[0,1]值越大实际圆形零件越接近于理想圆。 圆形度属于形状公差,圆形度误差值不大于相应的公差值,则认为合格,即e与理想圆的圆形度标准值满足es: |e-es|<0.1es。 (13) 通过MATLAB仿真实现不同圆形的圆形度如图1 所示。 从图1可知,圆形度与圆的大小无关,只与接近理想圆的程度有关,比如e1=0.96,虽然半径比较小,但是相比半径比较大的(e3=0.80),其产品的圆形度质量较高。 算法流程:① 输入圆形零件图像;② 对圆形零件图像边缘像素点70%~80%抽样;③ 按式(7)和式(8)获得候选圆形零件;④ 按式(10)和式(11)计算候选圆形零件参数;⑤ 计算圆形度e,满足式(13),进行步骤⑥,否则按次品处理;⑥ 输出检测结果。 试验计算机配置为Intel Core i7-7700,3.6 GHz,16 GB 内存,通过Matlab软件编程实现圆形零件的处理和分析,获得圆心坐标和半径参数。 对圆形零件性能测试涉及到的算法有CNN、HT、RHT、PHT、SHT、IHT,这些算法与三坐标测量机测量的标准圆形零件数据(a=60,b=80,r=20 mm)对比分析,10次测量获得数据如表1所示。 图1 不同的圆形度Figure 1 Different roundness 从表1可以看出,6种算法中IHT的a、b、r平均值与标准值最为接近,测量效果较好。 图2给出了不同算法10次测量数据与标准数据的差值。 表1 测量数据 图2 测量差值Figure 2 Measurement difference 从图2可以看出,IHT算法可以获得比较精确的测量数值,其对a、b、r测量的最大差值分别为0.078,0.057,0.076,相比其他算法最大值都较小,同时差值波动比较平稳,证明了该算法的稳定性较好。 通过20次蒙特卡罗试验评价IHT、CNN、HT、RHT、PHT、SHT 6种算法的测量精度及有效性,并对圆形零件的圆形度的不确定度进行计算。圆形零件的圆形度通过一次累加生成序列和理想累加序列得到其最大差值eΔmax,那么圆形度测量的不确定度s为: (14) 式中: w——测试次数。 s越小越好,表示测量结果与实际值较接近。不同算法的测量圆形度的不确定度如图3所示。 从图3可知,IHT、CNN、HT、RHT、PHT、SHT 6种算法对圆形零件的圆形度的不确定度均值分别为0.053 3,0.082 7,0.078 5,0.072 5,0.065 5,0.058 1,相比CNN、HT、RHT、PHT、SHT算法,IHT算法分别减少了35.55%,32.10%,26.48%,18.63%,8.26%,测量精度较高。 完成20次圆形零件的圆形度的不确定度计算,每次消耗的时间如图4所示。 图3 圆形度的不确定度Figure 3 Uncertainty of roundness 图4 消耗时间Figure 4 Time consume 从图4可以看出,CNN、HT、RHT、PHT、SHT、IHT算法20次检测所需时间平均值分别为7.795,7.204,6.671,6.262,5.361,4.282 s,IHT算法耗时最少,相比CNN、HT、RHT、PHT、SHT算法的分别减少了45.07%,40.56%,35.81%,35.81%,20.13%,因此采用IHT算法对圆形零件检测具有较好的时效性。 (1) 针对圆形零件检测过程中存在的问题,试验提出了一种改进Hough算法的圆形零件检测方法。通过最小误差抽样,聚类算法避免了虚假圆心出现,圆形参数测量数据差值波动比较平稳,说明该方法在圆形零件检测中算法的稳定性较好。 (2) 在圆形零件检测中,存在圆形度偏低情况的出现,建立圆形度判定指标,大大地提高了检测精度。 (3) 研究中如何使得Hough变换与检测正确率建立自适应关系有待进一步改进,这将是今后研究的一个方向。1.3 圆形度计算
2 试验仿真
2.1 性能测试

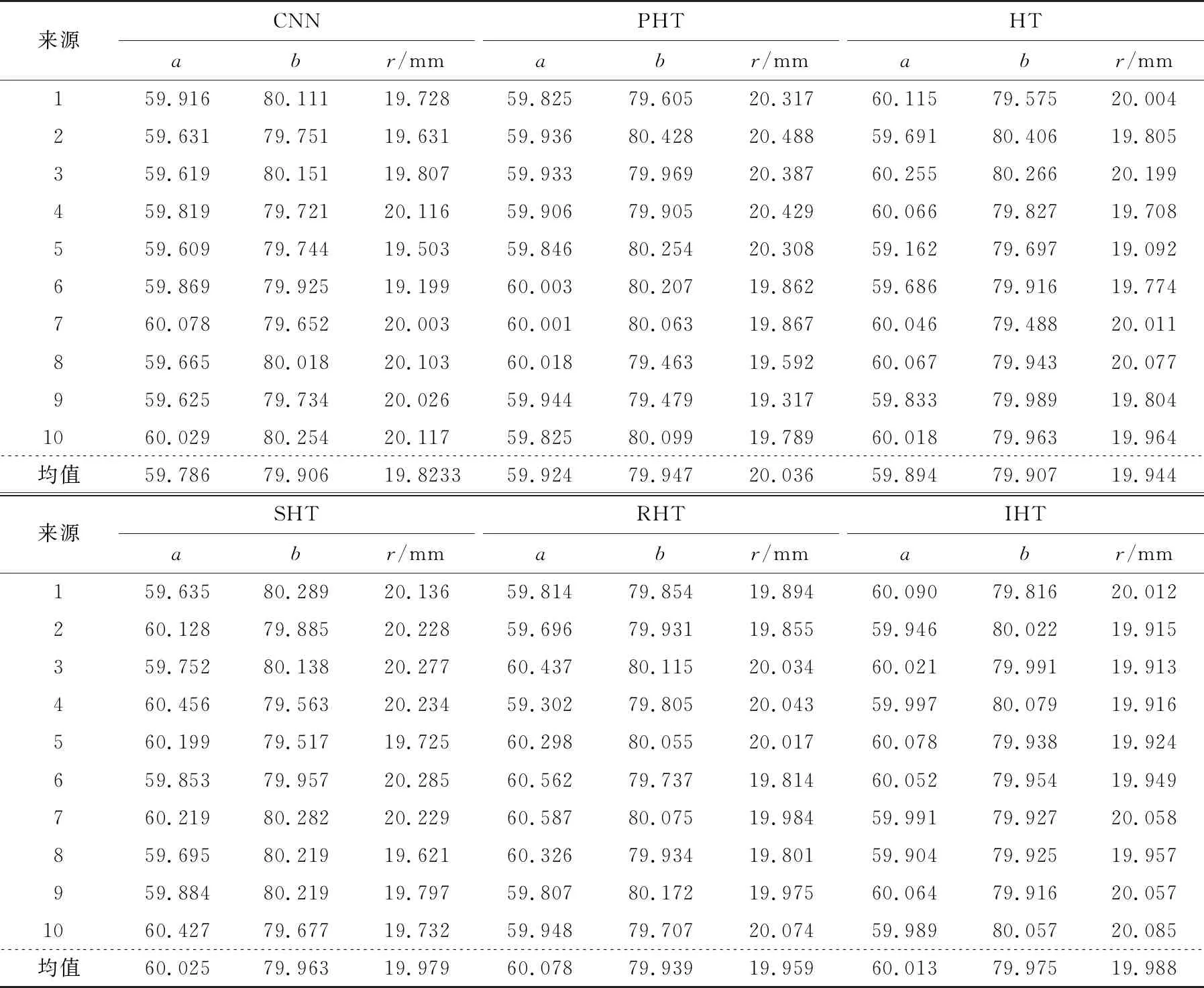
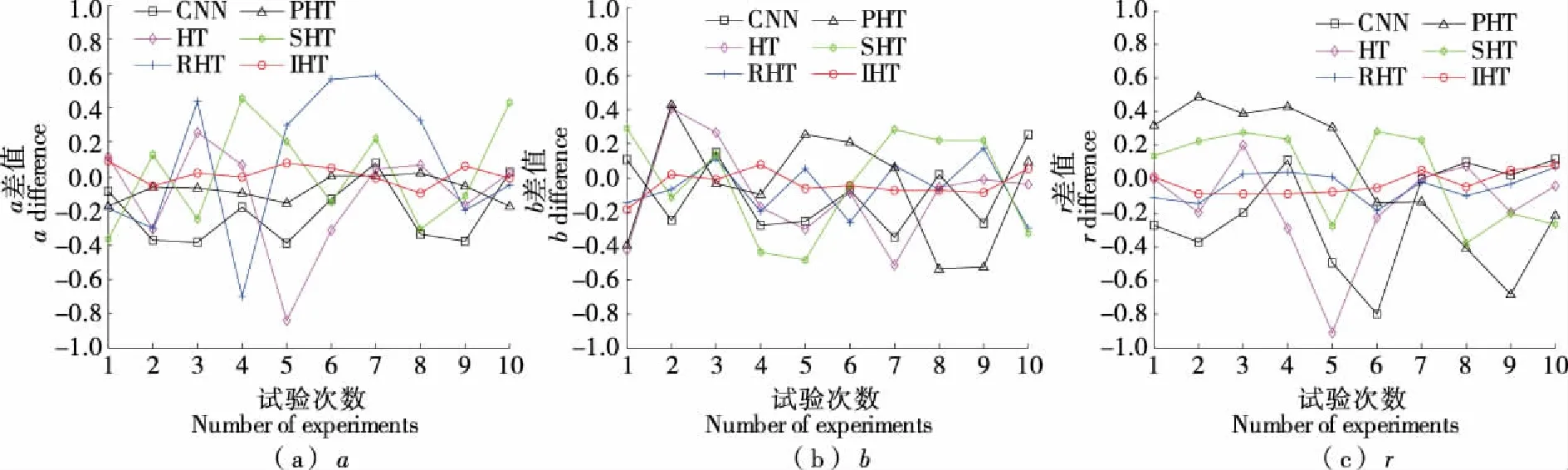
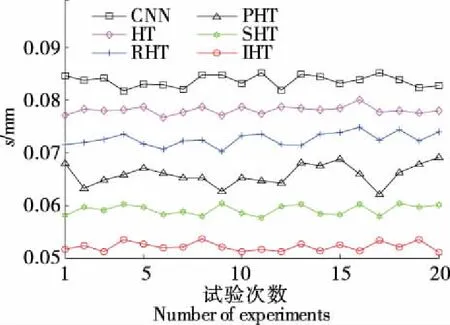
2.2 圆形度的不确定度计算
2.3 消耗时间
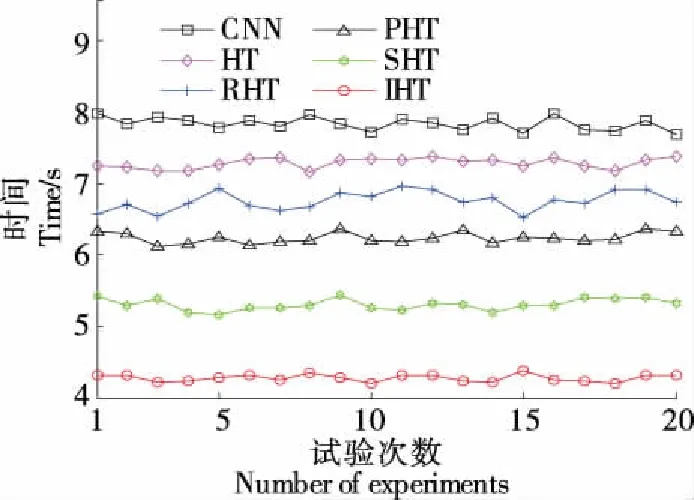
3 结论
