基于Oxley’s理论的300M钢正交切削加工变量的预测

2021-04-07张昌明

科学技术与工程 2021年6期

王运, 张昌明,2*, 张昱

(1.陕西理工大学机械工程学院, 汉中 723000； 2.陕西省工业自动化重点实验室, 汉中 723000)

300M钢(40CrNi2Si2MoVA)具有高强度、高硬度、耐疲劳及耐腐蚀等优良特性,已在国防军工及航空、航天领域得到了广泛应用,成为制造飞机起落架、车轮齿轮、火箭发动机外壳和中心主轴等主承力构件的主要材料[1-3],但300M钢高强度和高硬度的特性使其在切削加工中表现出切削力大、切削温度高、刀具磨损严重、表面质量差及加工效率低的特点,最终影响零部件的可靠性、疲劳性能、安全性以及使用寿命[4-6]。通过预测切削加工中应力、应变、切削力和切削温度等加工变量,可合理优化切削参数,从而提高加工表面质量,延长零部件使用寿命,因此对300M钢正交切削加工过程变量的预测十分重要。

目前中外学者对300M钢进行了一定的研究。司马中文等[7]设置了高速干车削300M钢试验,分析了表面粗糙度及残余应力与车削参数的关系,并得出了进给量是影响表面粗糙度的重要因素,切削速度和切削深度是影响残余应力的重要因素结论；Liu等[8]对300M钢设置了不同温度、应变速率条件下的压缩试验,研究了变形温度和应变速率对流动应力的影响规律,并构建了流动应力的模糊神经网络模型；郑光明等[9]设置了高速车削300M钢试验,研究了切屑变形、刀具寿命和刀具磨损机理,并得出车削300M钢时,切屑塑性变形严重,刀具发生前、后刀面磨损的结论；Zhang等[10]研究了加热温度和保温时间对300M钢奥氏体晶粒尺寸的影响,得出了奥氏体晶粒尺寸随加热温度和保温时间的增加而增大的结论,并建立了300M钢奥氏体晶粒生长模型；张慧萍等[11]设置了干式铣削300M钢试验,分析了铣削参数与刀具磨损之间的关系,并揭示了刀具磨损机理；Guo等[12]对300M钢进行了不同温度和应变速率的压缩试验,研究了300M钢的高温流动和动态再结晶行为,并构建了高应变速率下的再结晶体积分数模型和晶粒尺寸预测模型；章晓婷等[13]对300M钢进行了高温、低应变率下的热模拟压缩试验,分析了流动应力与变形温度和应变速率之间的关系,并建立了高温热变形材料本构方程；邢万强等[14]设置了车削300M钢试验,以移动热源理论为基础,结合不等距剪切区模型和试验获取的切削力、切屑厚度数据,并采用遗传算法获取300M钢的Johnson-Cook(J-C)本构方程参数。虽然中外学者对300M钢在力学性能、表面质量、刀具磨损等方面做了大量研究,由于缺少材料的本构方程,少有文献涉及对300M钢正交切削加工变量预测的研究,通过预测300M钢正交切削加工变量,可为工艺参数优化及切削加工研究提供理论指导。

将300M钢作为研究对象,以Oxley’s解析加工预测理论为基础,利用Labview软件编写了正交切削仿真算法,并开发了正交切削仿真模块,通过输入300M钢材料特性、切削条件以及刀具参数对300M钢正交切削加工变量进行了预测,依据仿真结果分析了不同切削参数对剪切角、切削力、切削温度和切削厚度等加工变量的影响规律,并验证了正交切削仿真模块的准确性。

1 正交切削试验

1.1 试验材料

试验材料300M超高强度钢棒材,几何尺寸为φ50 mm ×100 mm,其化学成分、机械性能和热物理性能如表1～表3所示[15-16]。

表2 300M钢的机械性能Table 2 Mechanical properties of 300M steel

表3 300M钢的热物理性能[16]Table 3 Thermo-physical properties of 300M steel[16]

1.2 试验条件

试验采用型号为C620-3型的普通车床进行车削试验,其最大工件回转直径为400 mm,最大工件长度1 000 mm；试验采用硬质合金刀具,其前角为-6°,后角为5°,刃倾角为0°,刀尖圆弧半径为 0.04 mm,车削过程使用微量冷却液；试验中切削力测量采用Kistler-9255B型号的三向测力仪系统,其三向测力仪系统包括A/D数模转换器(analog to digital converter)、电荷放大器和数据分析处理软件,则切削力测量示意图如图1所示。

图1 切削力测量示意图Fig.1 Schematic diagram of cutting force measurement

1.3 试验方案与结果

根据试验条件,将主轴转速、进给量和切削深度作为车削参数,为使外圆车削符合正交切削条件,在满足刀具性能的前提下选取大切深、小进给[17],并将切削深度作为常量,主轴转速和进给量作为变量,最后选取切削力的平均值作为每种切削条件下的试验值,其试验方案与结果如表4所示。

2 正交切削仿真模块

2.1 正交切削过程解析加工预测理论

以Oxley’s解析加工预测理论为理论基础,该理论是基于实验塑性流动场的滑移线场分析和应变率分析的切屑形成模型,符合实际的切削加工过程。切屑形成模型如图2所示,该模型包含第一变形区(主变形区)和第二变形区(刀-屑接触区),且第一变形区假设为平行变形区,第二变形区假设为等厚度变形区。剪切面MN位于第一变形区,其MN线被视为位于切屑形成区滑移线场中心处的直线型滑移线,对剪切面MN的分析如下。

lMN为剪切面MN的长度；U为切削线速度；Vs为剪切速度；V为滑移速度；t3为切屑厚度；t1为切削厚度；FC为主切削力；FT为进给力；R为切削合力；Fs为剪切力；FN为剪切面处法向切削力；F为刀-屑接触处的摩擦力；λ为摩擦角；N为刀-屑接触处的法向力；θ为切削合力(R)与剪切面MN间的夹角；Δd为剪切区宽度图2 切屑形成模型Fig.2 Chip formation model

剪切面MN处的应变假设均匀分布,且为第一变形区内总应变的1/2,其计算公式为

(1)

式(1)中：γMN为剪切面MN处的应变；α为刀具前角；φ为剪切角。

剪切面MN处的剪切应变率假设均匀,且与剪切速度(Vs)成正比,与剪切面长度(lMN)成反比,其计算公式为

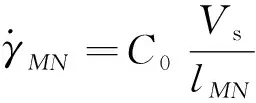
(2)

剪切速度表达式为

(3)

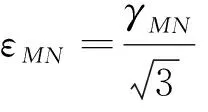
(4)

(5)

剪切面MN处的剪切流动应力(kMN)可由Von Mises 屈服准则求得

(6)

剪切面MN处的平均温度(TMN)计算公式为

TMN=Tw+ηΔTxy

(7)

(8)

式中:η为剪切面处塑性功与总塑性功的比值，0η1；ΔTxy为切屑形成的塑性变形区的温升；t1为切削厚度,相当于车削中的进给量(f)；ρ为材料密度；ω为材料比热容；t2为切削宽度,相当于车削中的切削深度(ap)；剪切力Fs可由式(9)求得；ψ为塑性功转化为工件温升的比例,0ψ1，可由布思莱德经验公式[式(10)]求得

(9)

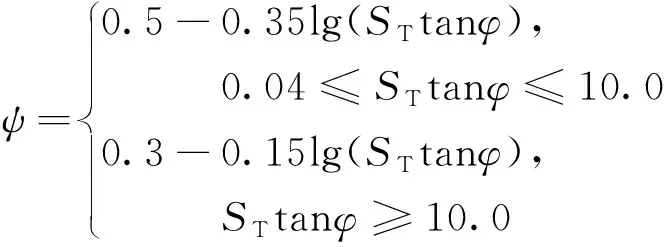
(10)

式(10)中：无量纲热值ST计算公式为

ST=ρωUt1/M′

(11)

式(11)中:M′为材料热导率。

第一变形区处的切削合力(R)计算公式为

(12)

FC=Rcos(λ-α)

(13)

FT=Rsin(λ-α)

(14)

t3=t1cos(φ-α)/sinφ

(15)

λ=θ+α-φ

(16)

式(16)中：切削合力(R)与剪切面MN间的夹角(θ)计算公式为[18]

(17)

式(17)中:neq为应变硬化指数，其计算公式为[18]

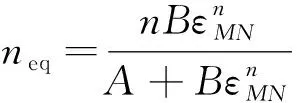
(18)

剪切面N点的法向应力(σ′N)可通过滑移线场的应力平衡方程和J-C流动应力模型得出，其计算公式为

(19)

第二变形区(刀-屑接触区)假设为等厚度变形区,且接触面处没有滑动,应力状态均匀。因此刀-屑接触区的等效最大应变速率可依据Von Mises屈服准则求得

(20)

刀-屑接触长度(h)计算公式为

(21)

刀-屑接触区的平均温度(Tint)计算公式为

Tint=Tw+ΔTxy+ξΔTM

(22)

式(22)中:ΔTM为刀-屑接触区的最大温升；ξ为刀-屑接触区平均温升与最大温升的比值，0≤ξ≤1。

ΔTM可由布思莱德公式得出，其计算公式为

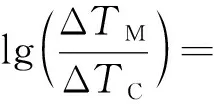
(23)

式(23)中:ΔTC为切屑内的平均温升,其计算公式为

(24)

式(24)中:F为刀-屑接触处的摩擦力,其计算公式为

F=Rsinλ

(25)

刀-屑接触处的法向力(N)的计算公式为

N=Rcosλ

(26)

刀-屑接触处最大剪切应变(γint)计算公式为

γint=2γMN+0.5γM

(27)

式(27)中：γM为刀-屑接触处总剪切应变,其计算公式为

(28)

刀-屑接触处的等效应变(εint)计算公式为

(29)

当求出刀-屑接触区的应变和应变率后,则刀-屑接触区的流动应力(kchip)为

(30)

刀-屑接触区的摩擦剪切应力(τint)为

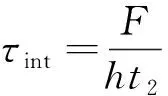
(31)

假定刀-屑接触区的法向应力分布均匀,则N点的法向应力(σN)为

(32)

2.2 正交切削仿真算法及仿真模块

在实际切削过程中剪切角(φ)、剪切面长度与主剪切区厚度的比值(C0)以及刀-屑接触面塑性变形区厚度与切屑厚度的比值(δ)是不断变化的,但学者往往将其作为定值进行研究,因此为了准确地预测300M钢正交切削加工过程变量,采用迭代思想来确定每种切削条件下的φ、C0和δ,并将上述Oxley’s解析加工预测理论利用Labview软件编写了正交切削仿真算法,其仿真算法思路如下:首先给定φ、C0和δ的范围及步长,然后根据上述公式并通过计算机程序不断迭代来确定φ、C0和δ的值,当刀-屑接触区的摩擦剪切应力(τint)等于其流动应力(kchip)时,φ迭代终止并得出此时的φ；当由两种方法得出的N点的法向应力相等(即σN=σ′N)时,C0迭代终止并得出此时的C0；最后当主切削力(FC)和进给力(FT)最小时,δ迭代终止并得出此时的δ,当φ、C0和δ确定后,通过相应的公式可计算出第一变形区和第二变形区内的应力、应变、切削力、切削温度和切屑厚度等切削过程变量。正交切削仿真算法流程如图3所示,依据仿真算法流程图,利用Labview编程软件开发了正交切削仿真模块,该正交切削仿真模块只需输入材料特性、切削条件以及刀具参数,便可直接预测出切削力、切削温度、剪切角、应力、应变、切屑厚度等切削加工变量,可为工艺参数优化及切削加工研究提供理论指导。

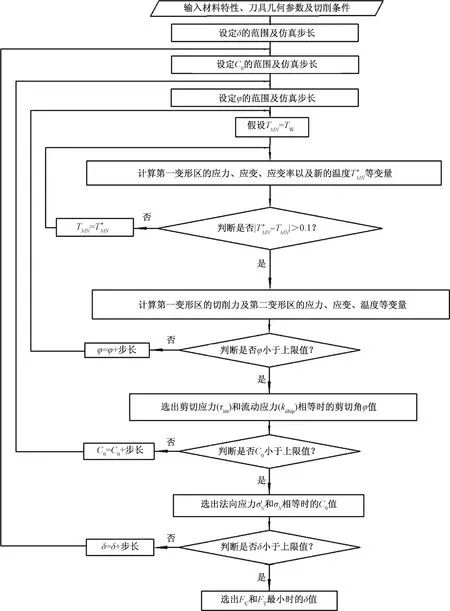
图3 正交切削仿真算法流程图Fig.3 Flow chart of orthogonal cutting simulation algorithm

3 300M钢正交切削仿真预测与正交仿真模块的验证

3.1 300M钢正交切削仿真预测

利用正交切削仿真模块对300M钢切削加工变量进行预测,仿真模块中涉及的材料特性:采用文献[14]基于移动热源理论所求出的300M钢J-C方程参数,即材料静态屈服应力A=1 302.6 MPa,强度系数B=695.3 MPa,应变强化指数n=0.297，应变率的敏感程度C=0.004 8,热软化效应的敏感程度m=0.73；300M钢的热物理参数如表3所示,室温为20 ℃,参考应变率为1 s-1。仿真模块中采用的刀具参数和切削条件均与试验相同,其300M钢正交切削仿真参数的设置如图4所示；通过仿真计算得出了每种切削条件下的切削加工变量,如表5所示；分析了不同切削参数对切削力、切削温度、应力、切屑厚度等加工变量的影响,如图5所示。

图4 300M钢正交切削仿真参数的设置Fig.4 Setting of simulation parameters of 300M steel orthogonal cutting

由表5可知，不同切削参数对剪切面长度与主剪切区厚度的比值(C0)影响较小,其值范围在6～7,不同切削参数对剪切角(φ)影响也较小,其值范围在20°～30°,可为切削加工研究提供理论指导。不同切削参数对应变的影响不大,刀-屑接触区的应变远大于剪切区的应变,且刀-屑接触区的应变率也远大于剪切区的应变率。

表5 300M钢正交切削仿真模块的仿真结果Table 5 Simulation results of 300M steel orthogonal cutting simulation module

由图5(a)可知，随着主轴转速的增加,主切削力和进给力均呈下降的趋势,这是由于主轴转速的增加,材料变形减小,同时热量不易传出,导致材料热软化效应增强,摩擦力减小,所以表现出切削力呈现下降的趋势。由图5(b)可知，随着进给量的增加,主切削力和进给力均呈上升的趋势,这是由于进给量的增加,材料变形增加,材料变形抗力和摩擦抗力增加,所以表现出切削力呈现上升的趋势。图5(c)、图5(d)分别表示温度与不同转速和进给量的关系。由图5(c)可知，随着主轴转速的增加,刀-屑接触区的平均温度略呈上升趋势,剪切区的平均温度几乎无变化,且刀-屑接触区的平均温度远高于剪切区的平均温度,这是由于主轴转速的增加,切削产生的热量不易及时传出。由图5(d)可知，进给量对剪切区温度和刀-屑接触区温度的影响与主轴转速对其的影响相同。图5(e)、图5(f)分别表示应力与不同转速和进给量的关系。图5(e)可知，随着主轴转速的增加,刀-屑接触区的流动应力略呈下降趋势,剪切区的流动应力几乎无变化,且剪切区的流动应力高于刀-屑接触区的流动应力,这是由于主轴转速的增加,材料的热软化效应增强,因此流动应力下降。由图5(f)可知，进给量对剪切区流动应力和刀-屑接触区流动应力的影响与主轴转速对其的影响相同。由图5(g)可知，随着主轴转速的增加,切屑厚度整体呈下降的趋势。如图5(h)所示:随着进给量的增加,切屑厚度呈上升的趋势。

3.2 正交切削仿真模块的验证

为了验证正交切削仿真模块的正确性,利用正交切削仿真模块获得的300M钢的主切削力和进给力的仿真结果与AdvantEdge软件仿真结果以及试验结果进行对比分析。由于切削深度与进给量的比值较大,因此选取AdvantEdge软件中二维切削仿真模型进行仿真计算,可在保证切削力仿真精度的前提下缩短仿真时间[19-21],将300M钢的JC方程参数以及热物理参数以自定义材料的形式输入到AdvantEdge软件中,刀具参数和切削条件的设置与试验相同,其AdvantEdge软件仿真参数的设置如图6所示。图6中,User Defined Parameter表示自定义参数；Parameter表示参数；Comment表示解释；Value表示数值；UMATPAR01表示材料子程序参数01；UMATPAR02表示材料子程序参数02；UMATPAR03 表示材料子程序参数03；UMATPAR04表示材料子程序参数04；UMATPAR05表示材料子程序参数05；UMATPAR06表示材料子程序参数06；UMATPAR07表示材料子程序参数07；UMATPAR08表示材料子程序参数08；T-room表示室温；T-melt表示材料熔点；rate0表示比率；Append表示添加；Delete表示删除；OK表示确定；Cancel表示取消；Turning Process Parameters表示车削工艺参数；Feed(f)表示进给量；Depth of cut(doc)表示切削深度；Length of cut[loc]表示切削长度；Cutting speed[v]表示切削速度；Initial temperature[To]表示初始温度；Workpiece表示工件；Workshop View表示车削视图；Tool表示车刀；Simulation Model表示仿真模型。当每种切削条件下的仿真计算结束后,在切削稳定区读取5个数值,并求取平均值作为最终的仿真结果,其不同仿真方式的仿真结果与试验结果对比如表6、图7所示。

图6 AdvantEdge软件仿真参数的设置Fig.6 Setting of simulation parameters of Advantagedge software

如表6所示，采用正交切削仿真模块所获得的主切削力(FC)与试验测量值的最大误差为12%,最小误差为0.5%,平均误差为5.01%。但采用 AdvantEdge 软件所获得的主切削力(FC)与试验测量值的最大误差为19.9%,最小误差为11.1%,平均误差为14.86%。采用正交切削仿真模块所获得的进给力(FT)与试验测量值的最大误差为19.3%,最小误差为11.7%,平均误差为14.65%。但采用AdvantEdge软件所获得的进给力(FT)与试验测量值的最大误差为39.1%,最小误差为16.3%,平均误差为23.50%,其误差原因可能是:①仿真中采用的J-C方程参数与300M钢的实际J-C参数存在一定的误差；②仿真中采用的热导率及比热容与温度呈线性关系,与实际切削加工中材料的热导率和比热容存在一定的误差；③仿真中采用的硬质合金刀具,其性能与试验中的硬质合金刀具性能存在一定的误差。

表6 不同仿真方式的仿真结果与试验结果对比Table 6 Comparison of simulation results and test results of different simulation methods

如图7所示，采用正交切削仿真模块所获得的主切削力(FC)和进给力(FT)与试验测量值的误差较小,而采用AdvantEdge软件所获得的主切削力(FC)和进给力(FT)与试验测量值的误差较大,说明采用正交切削仿真模块所获得的主切削力(FC)和进给力(FT)与试验结果更吻合,因此该仿真模块能较好地预测正交切削加工变量。