考虑时间延迟的人工驾驶车辆与网联车辆混合交通流建模与分析
2021-04-07费瑞波李光磊
陈 杰,费瑞波,刘 燕,李光磊
(蚌埠学院 经济与管理学院,安徽 蚌埠 233030)
在不久的未来,随着车联网技术的快速发展与逐步成熟,道路上将出现由网联车辆和人工驾驶车辆混合构成的交通流。由于人工驾驶车辆和网联车辆的驾驶主体遵循不同的跟驰规则,在混合交通流中可能诱发速度冲突和车头时距震荡等问题。车联网技术的发展将面临道路上传统人工驾驶车辆和网联车辆共同存在的阶段,网联车辆能够通过车车通讯和车路通讯等技术改善混合交通流的特性[1-3],缓解交通拥堵。针对混合交通流的研究,主要涉及:ACC/CACC车辆与人工驾驶车辆组成的混合交通流;自动驾驶车辆、网联车辆和人工驾驶车辆组成的混合交通流。
当前针对混合交通流的稳定性研究中,网联车辆跟驰模型主要还是建立在均一交通流情况下,并未考虑交通流的异质性对跟驰状态的影响,亦没有考虑相邻车辆类型的不同引起的交通流特性差异。因此,基于车辆网技术提出一种新的加速度模型框架,综合考虑了时间延迟、多前车速度反馈以及后视效应对主车辆的影响。通过稳定性分析和数值仿真,解析了模型参数取值对混合交通流通行能力与稳定性的影响。
1 跟驰行为建模
为了捕捉传统人工驾驶车辆和网联车辆加速度决策过程的差异,提出了一个加速度模型框架,以解决当前微观跟驰模型在捕捉混合环境中跟驰行为变化方面的局限性。
2 网联车辆跟驰行为模型
考虑网联车辆的后视效应建立了车辆跟驰模型,其次添加多前车的速度差作为反馈控制项,最后根据车辆类型的差异引入不同的反应延迟。网联车辆跟驰模型如式(1)所示:
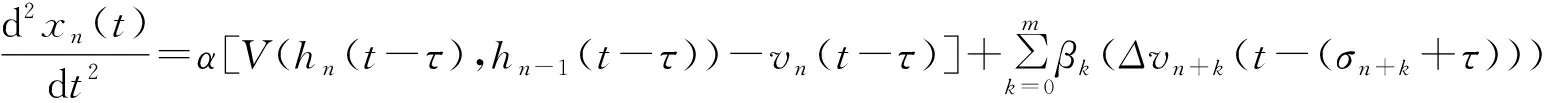
(1)
式中:α表示网联车辆的灵敏度;hn(t)表示t时刻车辆n与前车的车头间距;vn(t)表示t时刻车辆n的速度;τ表示人驾车驾驶员反应延迟(0.5-1 s)或自动驾驶系统控制器反应延迟(0.05-0.2 s);σn+k表示网联车辆n与前方第k辆车信息交互的通讯延迟;βk表示网联车辆前方第k辆车与前车的速度差增益;m表示与网联车辆n信息交互的通讯车辆数。
在模型(1)中,网联车辆的加速度由两项决定:一是期望速度,其主要考虑了网联车辆的后视效应,添加了相邻后车跟驰间距对当前车辆的影响,见式(2):
V(hn(t-τ),hn-1(t-τ))=(1+p)V(hn(t-τ))-pV(hn-1(t-τ))
(2)
式(2)中:p称为平滑参数,表示网联车辆对后车的关注程度。多前方相邻车辆的速度差,见式(3):
Δvn+k(t-(σn+k+τ))=vn+k+1(t-(σn+k+1+τ))-vn+k(t-(σn+k+τ))
(3)
Zhu等[18]给出了优化速度方程,V(hn(t))表示第n辆车的优化速度方程。
(4)
式中:Vmax表示路段最大允许速度;hc表示车身长度。
人工驾驶车辆跟驰行为模型。驾驶员在决策过程中,对前车运动状态变化的感知存在一定的反应延迟。因此,基于FVD模型[4]引入驾驶员的反应延迟。人工驾驶车辆亦遵循式(4)的期望速度,其跟驰模型如式(5)所示:

(5)
式中:αp表示驾驶员的灵敏度;βp表示驾驶员的速度差增益。
3 稳定性分析
跟驰模型队列线性稳定性的研究方法较多,有文献将跟驰模型的表达式统一为加速度策略下的控制模型[5],模型的不稳定性条件:

(6)
式中:fv表示模型公式对速度的偏微分;fΔv表示模型公式对速度差的偏微分;fh表示模型公式对车头间距的偏微分;根据式(1),求得网联车辆跟驰模型的偏微分,根据文献[6]可知:
(7)
因此,网联车辆跟驰模型的稳定性条件可以记为:
(8)
同理可得人工驾驶车辆跟驰模型的稳定性条件:
α>2V′(h)-2βp
(9)
4 基于数值仿真的模型解析
由于网联车辆的通讯车辆数差异和交通密度的变化,混合交通流可能会表现出不同的特性。由稳定性分析发现,灵敏度、平滑参数和通讯车辆数将共同影响交通流的稳定性,因而设计了这三个参数在不同取值时对交通流基本图和微观跟驰特性的影响实验[7-11]。仿真路段长度为1600 m,道路上有n辆车,其中车辆n为头车,其他相关参数如表1所示。
4.1 交通流基本图分析
本次仿真将分别讨论上述三个参数的变化对网联车辆交通流和混合交通流基本图的影响。在仿真过程中,通过固定路段长度,调整路段上车辆的数量实现交通流密度变化。仿真时长为2000 s,其中,选择第1700 s至第1800 s的仿真结果求平均值,进而得到网联车辆交通流和混合交通流的基本图。
(1)网联车交通流。为了分析灵敏度、平滑参数和通讯车辆数对网联车辆基本图的影响,在仿真实验中设置了三组不同参数取值环境:(1)灵敏度α=1.0,1.3,1.6,1.9,平滑参数p=0,通讯车辆数m=0;(2)平滑参数p= 0.1,0.2,0.3,0.4,灵敏度α=1.0,通讯车辆数m=0;(3)通讯车辆数m=0,1,2,3,灵敏度α=1.0,平滑参数p=0。 仿真结果如图1所示,图1中a、b和c分别表示不同灵敏度,平滑参数和通讯车辆数情况下网联车辆基本图表现。
由图1(a)可以发现:当密度ρ小于关键密度ρc时,此刻网联车辆跟驰的自由度较高。由图1(b)可以发现:当密度较小时,由于前后车辆跟驰间距较大,因而车辆的跟驰主要依赖于前车的运动状态,此刻较小的光滑参数将带来较大的通行能力;由图1(c)可以发现:当路段密度小于关键密度ρc时,网联车辆能够通过车车通讯获取前方交通流状况,提前调整自身状态,提高路段通行能力。

表1 相关仿真参数

图1 不同情况下的网联车辆
(2)50%渗透率混合交通流。为了分析网联车辆对其与人工驾驶车辆组成的混合交通流的影响,设计了与第3节条件相同的对照仿真实验,其中,网联车辆渗透率为50%。仿真结果如图2所示。对比图1发现,无论是网联车交通流还是混合交通流,均在一定范围内受灵敏度、平滑参数和通讯车辆数的影响。
超出此范围,交通流将对这三个参数不敏感。不同的是,混合交通流的密度范围变化要大于网联车流。

图2 不同情况下的混合交通流
(3)不同渗透率混合交通流。为了分析在所述加速度模型框架下,不同网联车辆渗透率对混合交通流基本图的影响,设定以下仿真环境:渗透率b=0,0.2,0.4,0.6,0.8,1.0,灵敏度α=1,平滑参数p=0.3,通讯车辆数m=2。仿真结果如图3所示。
当渗透率小于60%时,通行能力的增加较为缓慢。当渗透率大于60%时,所述加速度模型框架能够大幅度提高路段的通行能力。另外,可以发现在密度ρ=0.1附近,由于网联车的通讯延迟累积和前车的速度反馈等因素导致其实际跟驰加速度与期望加速度的偏差增大,因而通行能力存在急剧下降过程,且渗透率越高,此过程越明显。由于传统车辆和网联车辆的输入顺序是随机的,因而低渗透率混合交通流存在局部的波动性。

图3 不同渗透率的混合交通流
4.2 网联车交通流稳定性分析
为了探究所述加速度模型框架中灵敏度、平滑参数和通讯车辆数的摄动对网联车流的作用效果,引入了100辆网联车[12-16]。仿真时间为1800 s,其中将第1700 s作为数据采集时刻。
(1)不同灵敏度的网联车交通流。为了分析灵敏度的摄动对网联车交通流的影响,设计了以下仿真环境:灵敏度α= 0.85,0.95,1.05,1.15,平滑参数p =0,通讯车辆数m=0。车头间距表现如图4所示,在网联车交通流中,很小的灵敏度变化就能实现跟驰间距的稳定。由图5可以发现,随着灵敏度的增大,网联车辆的速度变化范围逐渐集中,趋于路段的平均车速。

图4 网联车辆在不同灵敏度情况下的车头间距

图5 网联车辆在不同灵敏度情况下的车头间距-速度图
(2)不同平滑参数的网联车交通流。为了分析平滑参数的摄动对网联车交通流的影响,设计了以下仿真环境:平滑参数p=0.1,0.2,0.3,0.4,灵敏度α=1,通讯车辆数m=0。仿真结果如图6和图7所示,可以发现随着平滑参数的增大,自动车辆跟驰间距和速度变化震荡范围增大,且震荡频率逐步增大。因此,在密度较小时,适宜采用较小的平滑参数,其与4.1节中结论相印证。
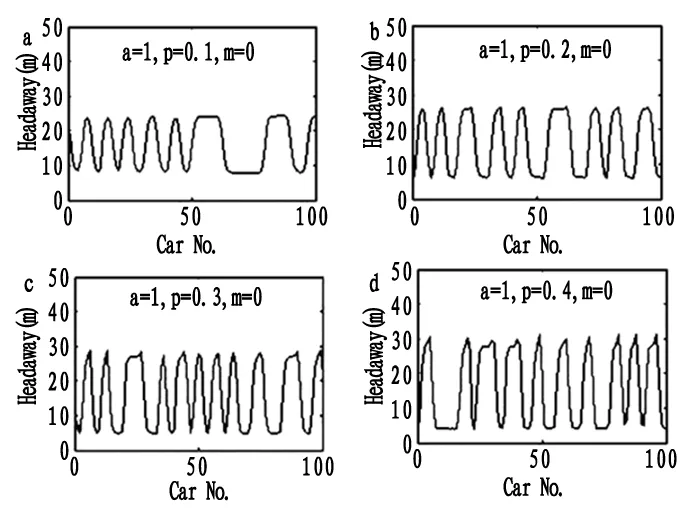
图6 网联车辆在不同平滑参数情况下的车头间距

图7 网联车辆在不同平滑参数情况下的车头间距-速度图
(3)不同通讯车辆数的网联车交通流。为了分析通讯车辆数的摄动对网联车交通流的影响,设计了以下仿真环境:通讯车辆数m=0,1,2,3。灵敏度α=1,平滑参数p=0。仿真结果如图8和图9所示,可以看出当交通流密度较小时,随着通讯车辆数的增加,网联车辆提前获取多前车运动状态信息,其波动频率降低,车头间距和跟驰速度亦趋于稳定。
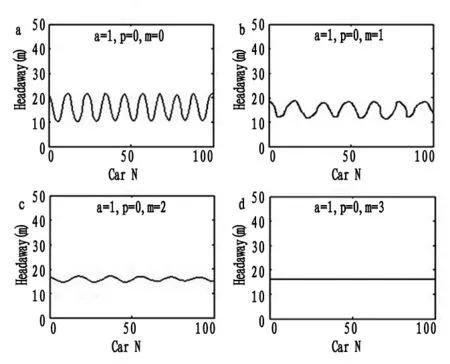
图8 网联车辆在不同通讯车辆数情况下的车头间距
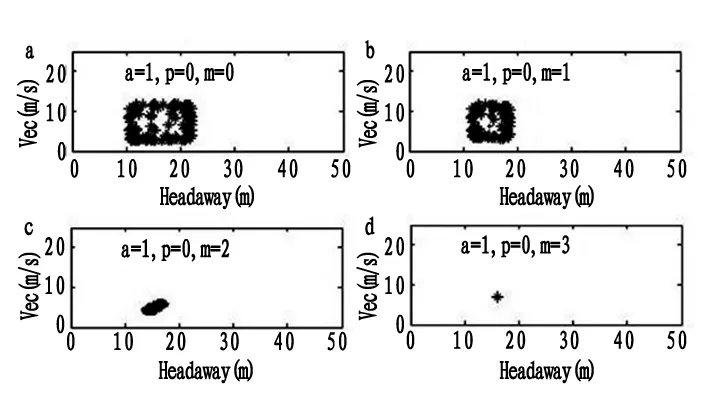
图9 网联车辆在不同通讯车辆数情况下的车头间距-速度图
4.3 混合交通流稳定性分析
为了分析灵敏度、平滑参数和通讯车辆数对混合交通流的影响,采用了50%的网联车辆渗透率进行研究。在仿真实验当中,我们设置了三组不同参数取值环境:(1)灵敏度α=1.0,1.3,1.6,1.9,平滑参p=0,通讯车辆数m=0;(2)平滑参数p=0.1,0.2,0.3,0.4,灵敏度α=1.0,通讯车辆数m=0;(3)通讯车辆数m=0,1,2,3,灵敏度α=1.0,平滑参数p=0。仿真结果如图10、图11和图12所示。
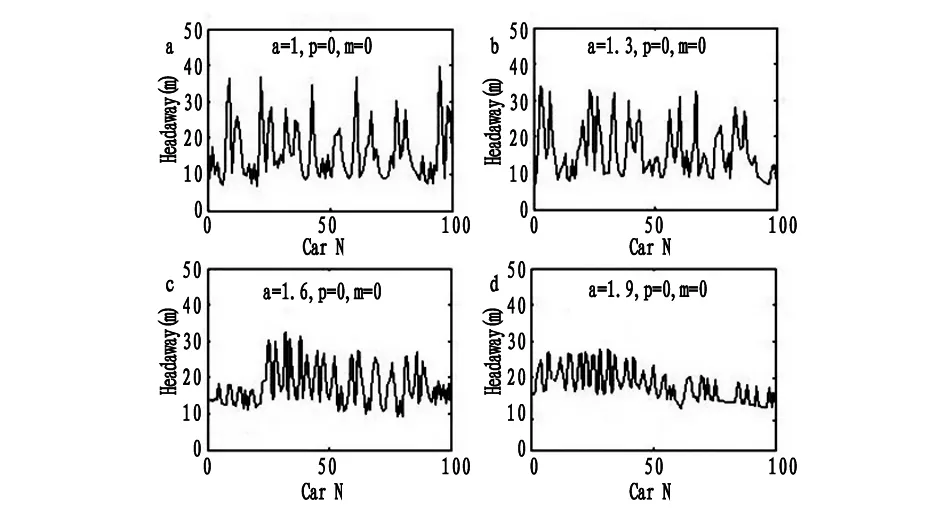
图10 混合交通流在不同灵敏度情况下的车头间距
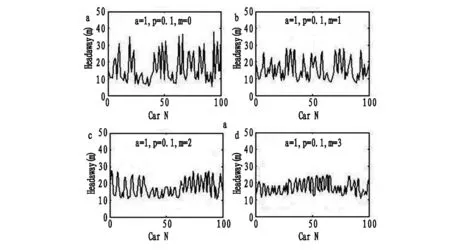
图12 混合交通流在不同通讯车辆数情况下的车头间距
图10中可见,当灵敏度较小时,混合车流的车头间距波动范围较大,车流极不稳定。随着灵敏度的增加,车头间距逐渐缩小至一个稳定的范围。横向对比图5发现,混驾交通流网联车辆灵敏度的增大,虽然降低了跟驰间距的波动范围,但是其波动频率并没有明显降低。
图11中发现,随着当前车辆对后车的关注程度增大,车头间距的变化范围也增大。因此在低密度情况下,应该降低对后车的关注,以提高交通流的稳定性。横向对比图7发现,平滑参数在一定程度上能够调节交通流的稳定性,但是其调节幅度较小。
图12中发现,随着通讯车辆的增加,车头间距的波动迅速降低,当通讯车辆数达到三辆时,车头间距的波动范围也基本稳定。因而在低密度情况下通讯车辆数的增加,能够极大减弱混合交通流的波动性,稳定车辆的跟驰间距。
综上,低密度情况下,提高灵敏度和通信车辆数或降低对后车的关注程度都可以提高交通流的稳定性,其中交通流的稳定性对灵敏度和通讯车辆数的变化更为敏感,而平滑参数适合作为一种微调或者补充的形式,调控交通流的波动。高密度情况下,与之相反。
5 结论
针对网联车辆的控制方式,探讨了其在混合交通流中作用机理及工作方式,研究了人工驾驶车辆与网联车辆构成的混合交通流的跟驰特性,提出了一个加速度模型框架,包括:考虑前后跟驰间距的优化速度函数、多前车速度差反馈控制和时间延迟的网联车跟驰模型和考虑时间延迟的人工驾驶车辆跟驰模型;接着,根据Wilson方法证明了交通流的跟驰稳定性受网联车的灵敏度、平滑参数和通讯车辆数的取值影响;最后,采用数值仿真的方法解析了上述三个参数对基本图和微观交通流稳定性的影响。仿真结果表明,无论是网联车交通流或混合交通流,在一定范围之内受灵敏度、平滑参数和通讯车辆数的影响。超出此范围,交通流将对这三个参数不敏感。不同的是混合交通流的密度范围变化大于网联车流。混合交通流随着密度的增加,其通行能力存在突降的过程,且渗透率越高,此过程越明显。通过微观解析可以发现,在交通流密度一定时,调节上述三个参数的值能够不同程度上提高混合交通流的稳定性,且参数的最优值可以根据当前密度所处关键密度ρc的方向进行寻优取值。
