基于三维全向磁感应的水下定位技术研究

王志强，张美燕，蔡文郁

(1.杭州电子科技大学电子信息学院，浙江 杭州 310018;2.浙江水利水电学院电气工程学院，浙江 杭州 310018)

0 引 言

随着海洋领域研究的不断深入，海洋探索与科考以及海洋资源的开发与利用，引领了海洋图像数据收集、自然灾难预警、生态环境检测与监控、水下机器人导航等一系列水下信息技术的发展[1]，其中水下定位技术扮演重要角色。以水下传感器网络为例，在海洋环境监测应用中，准确获取传感器网络节点的位置信息不仅能提高环境监测的效率，而且能在信息传递中大大降低传感器网络的功耗[2]。目前，水下定位方案利用的物理介质主要是声信号与光信号。文献[3]提出一种基于最小二乘法估计的对称修正算法，提高了水下声波定位的精度。依靠点对点的信号传递难以实现目标的精确定位，为此，文献[4]根据声学通道在水中传递的时间差，采用周期性的三角接收阵列扫描目标声呐的声学信号，提出一种三维被动式定位方案。光信号因其在水中急剧衰减的特性使其只能作为近距离水下定位的解决方案[5]。文献[6]提出一种基于电磁波信号强度的3D定位框架，利用电磁波在水中衰减程度与距离的关系，分别实现了无人潜航器(Unmanned Underwater Vehicle, UUV)水下对接工作和遥控无人潜航器(Remote Operated Vehicle, ROV)的实时定位追踪。

水体介质对磁信号衰减的影响很小，可将其作为水下定位技术的基础来研制水下定位系统。文献[7]简化了磁通信的通信结构，将三维空间中的方向位置判断简化为二维平面的位置判断，提出一种基于磁通信的室内移动机器人定位方案。三维正交线圈两两垂直的结构设计，使其在三维空间中的磁场分布与空间位置具有一定几何关系。通过此关系，感应节点分别感应出发射节点的3个磁线圈的磁感应强度，通过计算得出感应节点所处的位置信息。本文研究三维正交线圈在空间位置测得的磁场值与该点离信号发射节点的位置关系，通过感应节点的磁感应强度即可得到其空间坐标，提出一种基于三维全向磁感应的水下定位技术，为建立良好的磁通信信道奠定技术基础。

1 三维磁感应定位算法原理

1.1 系统框架

图1 基于三维全向磁感应的水下定位模型

三维全向线圈作为源节点，其中3个正交线圈在空间任意一点的磁感应强度存在一定差异，磁场分布与空间位置具有一定的几何关系。因此，本文采用3个互相正交的磁感应线圈作为信号源，依次在空间产生相互正交的分布磁场，再由三维正交磁感应线圈依次感应出不同方向的磁感应强度，最终根据磁场分布的空间几何关系与磁偶极子的磁场分布模型反推出该点的空间位置信息。基于三维全向磁感应的水下定位模型如图1所示。图1中，线圈a,b,c分别表示发送线圈垂直于z,y,x轴的子线圈，线圈A,B,C表示接收线圈垂直于z,y,x轴的子线圈；θ1,θ2,θ3分别表示感应节点和发射节点间连线与发射节点线圈所处平面的夹角；B1,B2,B3分别表示感应节点A,B,C子线圈感应出的磁感应强度；R表示感应节点和发射节点间的距离。

1.2 磁偶极子磁感应分布模型

图2 点p与点p′的空间几何关系

通电线圈在三维空间的磁场分布模型主要有磁偶极子模型和有限元积分模型[7]。其中，有限元积分模型在精度方面更加准确，在近距离磁感应强度的分析计算中精度更高。但当感应距离d远大于通电线圈的半径r时，磁偶极子模型的准确度与有限元积分模型的准确度趋于相同，相对误差只有0.030 5%[8]。这时，磁偶极子模型突显出计算量小、运算速率快等优势。本文方案是为了解决水下磁感应定位问题，应用场景中2个定位节点的距离均远大于定位线圈半径，符合磁偶极子模型应用条件，故选用磁偶极子模型作为系统框架中信号源的磁场辐射模型。

本文模型采用3组相互正交的线圈作为磁感应通信的源信号发射线圈，3组发射线圈依次向空间辐射经过调制的可变磁场。在远场条件下，整个通信线圈的磁感应分布模型由3组相互正交线圈的磁感应分布模型叠加形成，故文中只分析单组线圈的磁感应分布模型，磁感应线圈的空间位置如图2所示。图2中，线圈位于x轴与y轴所在平面，并垂直于z轴，线圈圆心经过坐标原点。线圈半径为r，x轴与y轴所在平面上任意一点p′到原点距离是R′，空间任意一点p到原点的距离为R。Bp′代表点p′的磁感应强度，Bx,Bz是其x,z轴上的分量。Bp代表点p的磁感应强度，Bx,By,Bz是其x,y,z轴上的分量。

根据Biot-Savart定律[9]，在单匝线圈(以线圈a为例)，满足R≫r的情况下，处于x轴与z轴所在平面上任意一点p′的磁感应强度为：

(1)

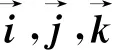
根据磁场叠加原理，N匝线圈在该点的磁感应强度为：

(2)

在空间任意一点的磁感应强度可以分解为沿坐标轴3个方向上的矢量和，则有：

(3)

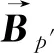
(4)

点p与点p′的空间几何关系如图2所示，其几何约束满足：

(5)

根据Biot-Savart定理，在半径r、电流I等变量相等的情况下，不同点的磁感应强度只与其据信号源位置的空间距离有关，且对应成比例。因此有：

(6)

由于单线圈磁感应分布空间对称性，空间任意一点在平行于线圈平面的磁感应强度分量与其所在位置的空间矢量对应成比例，因此有：

(7)

其中，

(8)

联立式(4)、式(6)、式(8)，得到空间任意一点p处的磁感应强度为：

(9)

根据式(9)所示磁场分布模型，线圈a的磁场分布仿真如图3所示。

图3 线圈a磁场分布图

1.3 三维正交磁感应定位理论模型

感应线圈在空间任意一点得出的磁感应强度由3个子线圈A,B,C得出的磁感应强度分量矢量运算得出。以线圈a为例，线圈a在空间任意一点的磁感应强度为：

(10)

式中，Ba表示源线圈a在该点的磁感应强度感应值，Bk(k=1,2,3)表示感应线圈在该点处感应出的Ba的3个分量值。

感应线圈在空间任意一点，测得源线圈在该位置依次辐射出的磁场的磁感应强度分别表示为Ba,Bb,Bc，其与源线圈的位置关系表示为[10]：

(11)

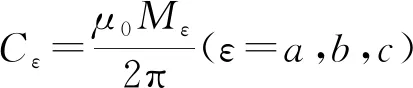
由空间几何关系可以得出该点的空间坐标值与cosθk(k=1,2,3)的关系为：

(12)

代入式(11)得到空间该点空间坐标x,y,z与该点3个磁感应强度Bε(ε=a,b,c)的关系：

(13)

式中，x2+y2+z2=R2。

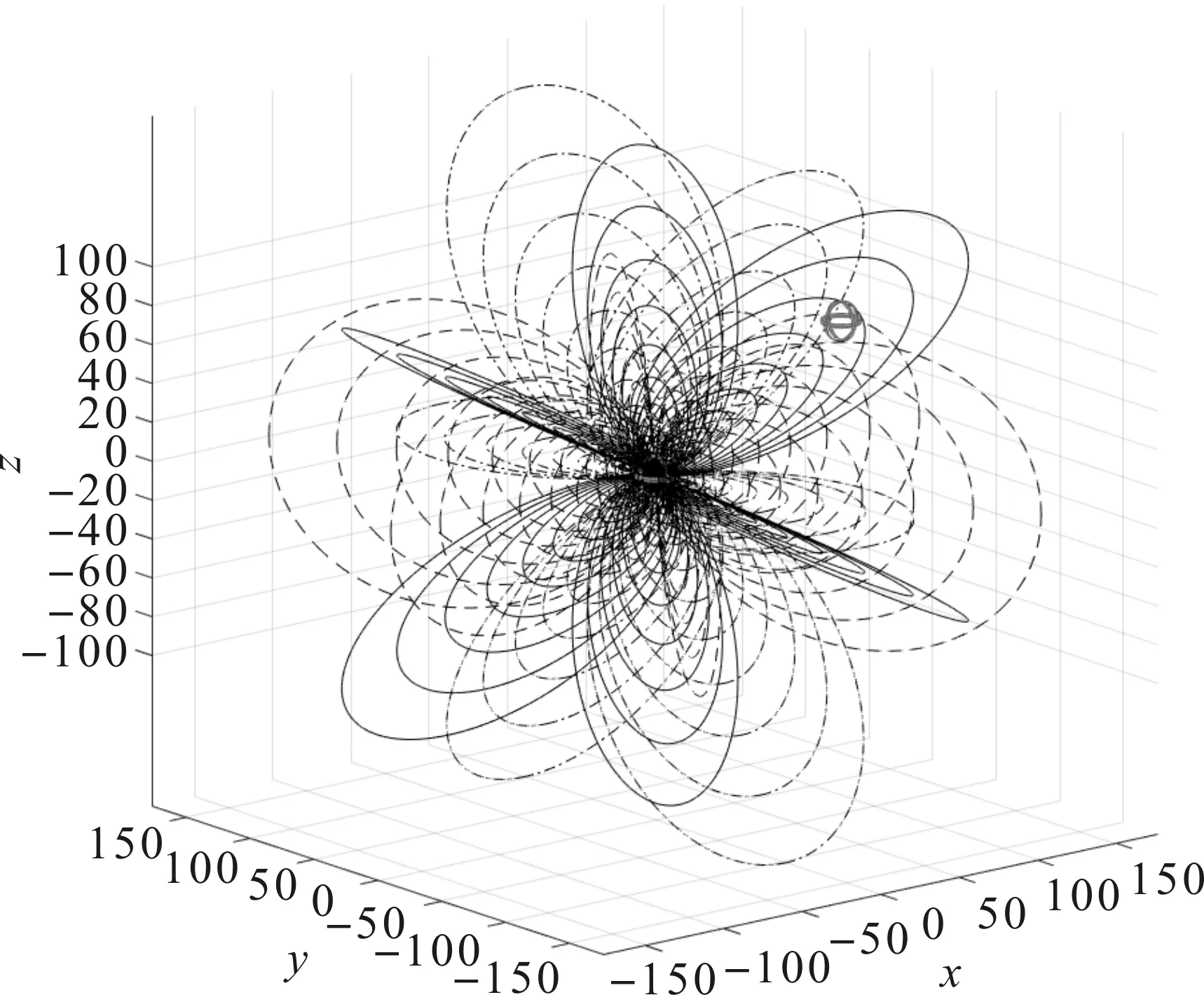
图4 三维正交磁感应定位模型

采用磁偶极子模型[11]进行仿真实验，得到的三维正交磁感应定位模型如图4所示。位于原点的发射节点的3个正交子线圈依次辐射出磁场信号，位于空间任意一点处的感应线圈依次感应出Ba,Bb,Bc。通过三维正交线圈磁感应定位算法计算出感应线圈距离原点的距离以及笛卡尔坐标值。如果信号发射节点的位置是空间任意一点，那么根据发射节点所在位置与原点的关系，通过坐标平移即可得到感应节点新的坐标位置[12-13]。

1.4 三维正交线圈磁感应定位算法

图5 定位流程图

三维正交线圈磁感应定位算法的定位流程如图5所示。将感应节点在空间任意一点采集的磁感应强度值代入定位方程，解算出坐标值，判断是否在预定卦限，判断成立则进行坐标转化输出最终坐标与距离，判断不成立则记录当前错误数据，并重新解算，直到得出在预定卦限的数据。

2 仿真结果与分析

采用MATLAB R2016仿真软件模拟三维磁感应线圈磁场分布的方式进行算法验证。通过加入高斯白噪声的方式模拟真实测试环境，并绘制加入噪声的三维线圈的磁场分布与计算感应节点处于任意空间位置的坐标。

仿真参数设置如下：源线圈设定为半径r=10 cm，匝数N=200，电流I=100 A的通电线圈；磁导率μ0=4π×10-7，直角坐标系下，x,y,z∈[-200,200]，分辨率为1 cm。计算源线圈在磁偶极子模型下的磁场分布，在加入随机噪声之后，绘制仿真后的三维方向下的磁场分布。磁场模型搭建好之后，在(-200，-100)∪(100,200)范围内随机选取20组坐标，在引入随机噪声的磁场环境下，采用三维磁感应定位算法计算得出坐标结果，并与实际坐标进行比较。

2.1 三轴正交线圈磁场分布仿真

三轴正交线圈磁场分布分别由3种不同形状的线条表示。为了使得磁场分布的层次结构更加清晰明了，每一组线圈的磁场分布只取6个方向，且略去靠近线圈中轴线上较为密集、不能闭合的磁感应线。引入的高斯白噪声信噪比分别为10 dB，15 dB，20 dB。位于原点的三维正交线圈辐射出的磁场在空间的理论磁场分布如图6所示，加入信噪比为10 dB的高斯白噪声后，理论磁场分布如图7所示。从图6和图7可以看出，高斯白噪声加入前后，磁感应分布改变但层次依然清晰。

图6 三维正交线圈理论磁场分布

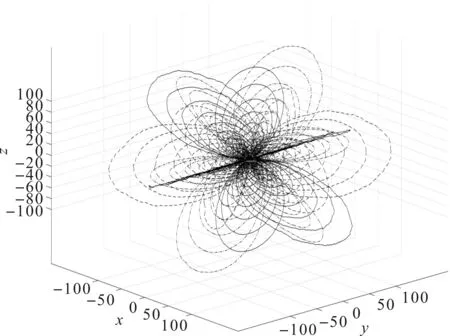
图7 三维正交线圈加入SNR=10 dB高斯白噪声的磁场分布

2.2 随机坐标定位仿真

通过测得空间任意位置、发射线圈的三维磁感应强度，采用三维正交线圈磁感应定位算法求出感应线圈相对于发射线圈的距离以及对应坐标值。在信噪比分别为10 dB，15 dB，20 dB高斯白噪声下，各生成随机的20个坐标，对2个节点的距离以及对应的坐标进行仿真，结果如图8和表1所示。因篇幅原因，表1只截取其中15组仿真结果。

图8 感应线圈实际距离与定位距离对比

表1 定位坐标与实际坐标对比

从图8可以看出，当信噪比为10 dB时，采用本文的定位算法计算得到的定位距离与实际距离偏差较大；当信噪比为15 dB, 20 dB时，定位距离与实际距离接近一致。从表1可以看出，当信噪比为15 dB时，定位算法的坐标精度达到30 cm以内；信噪比为20 dB时，定位精度达到20 cm以内。由图7可以看出，信噪比大于等于10 dB时，源线圈磁场分布比较理想。所以，将磁感应强度引入随机噪声之后，三维正交源线圈的磁场分布虽有一定程度的失真，但磁场分布结构依然清晰稳定，通过三维磁感应定位算法能够有效得出定位节点间的距离与坐标。

在信噪比为15 dB时，以50 cm为间隔，在[100,1 000]范围内，取19个x,y,z分量相同的坐标，计算其定位坐标，分析随着距离的增加，定位坐标与实际坐标的偏离情况，仿真结果如图9所示。

图9 不同距离下实际坐标与定位坐标对比图

从图9可以看出，在SNR为15 dB时，随着距离增加，定位坐标逐渐偏离实际坐标。在坐标分量值大于550 cm后，定位坐标偏离程度较大，所以，通过本文定位算法可以在550 cm内得到准确的定位坐标。

3 结束语

本文提出了一种基于三维全向磁感应线圈的水下定位技术。在一定强度的噪声干扰下，基于三维线圈下的定位模型可以得到准确的定位距离与较为准确的笛卡尔坐标，验证了运用三维全向磁感应线圈实现水下定位的可行性。在三维全向磁感应线圈进行水下磁通信的同时，实时测得2个通信节点的相对角度与距离，为通信节点的姿态调整提供角度信息，为良好的通信质量奠定基础。下一步将具体实现三维全向磁感应线圈的通信系统，将基于三维全向磁感应通信的水下定位技术应用于通信节点的姿态调整，以此获得更佳的通信质量，并进行实际水下测试。