密集信号环境下基于星座轨迹图调制识别算法

王希琳，沈 雷，赵永宽，张铭宏

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

0 引 言

现代无线通信技术日新月异，实际通信环境因为未知信号的出现变得越发复杂。在密集环境下对信号进行有效的侦查识别，在民用和军用领域都有十分广泛的应用价值。多进制幅相信号如多进制数字相位调制(Multiple Phase Shift Keying，MPSK)，多进制振幅相移键控(Multiple Amplitude and Phase Shift Keying，MAPSK)，多进制正交振幅调制(Multiple Quadrature Amplitude Modulation，MQAM)等作为卫星数传系统的主要调制方式，有着频谱利用率高的优点，有关这类信号的调制识别技术仍是当前值得关注的热点[1]。针对这类高阶幅相信号的识别问题，目前采用较多的是基于特征提取的模式识别方法，文献[2]采用多个高阶累积量构造的特征参数和随机森林分类器进行识别，有效提高了信号在低信噪比时的识别性能，但高阶累积量对参数估计要求高，且计算复杂，在嵌入式上实现困难。文献[3-4]利用信号幅值概率密度构造似然函数实现了MQAM信号的识别，然而，实际幅相信号的调制信息综合反映在幅值和相位分布上，该方法仅利用幅值信息，识别性能和可扩展性较差。

星座图能提供已调信号的幅相信息，因此基于星座图的识别算法具有很强的鲁棒性。文献[5]提出一种基于星座图相位信息的MPSK，MQAM信号联合识别算法，从聚类恢复后的星座图中提取相位个数作为统计量，由于只利用星座图相位信息，抗频偏性能较差。文献[6]提出基于星座图多特征联合方法实现常见幅相信号的识别，但星座点数越多时星座点间距越近越容易产生交叠，聚类点数特征受其影响较大，导致算法在低信噪比、频偏较大时性能不佳。文献[7]提出一种基于星座图幅度分布向量匹配的抗频偏卫星幅相信号调制识别算法，由于只利用了星座图的幅度概率密度信息，在低信噪比下星座点分布较为分散，各点间幅值差别较小，造成实际幅度分布与理论差异较大，算法识别效果不佳。且该方法统计量和模板构造过程平方阶使用较多，计算复杂度高。

目前，基于星座图的高阶信号识别算法多是针对理想解调情况。而在密集信号环境下，解调过程受相邻信号的频谱干扰和噪声影响，解调星座图往往会旋转且聚拢度不够，其特征与理想解调图形差异明显。由于幅值曲率分布受噪声影响较小，而轨迹信息又反映了每种信号特有的星座图结构，因此，本文采用星座图幅值曲率和轨迹信息作为识别特征参数，设计了一种密集信号环境下基于星座轨迹图的调制识别算法，性能优良，易于实现。

1 基于高阶幅相信号数字接收机的信号盲解调

1.1 密集幅相信号模型

本文所研究密集信号集合为{8PSK，16APSK，32APSK，16QAM，32QAM}，共5种调制方式，在密集高阶幅相信号环境下，信号模型表示为：

(1)

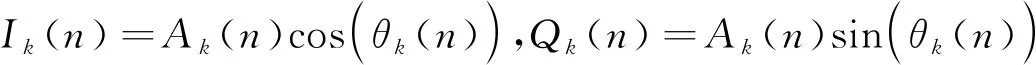
1.2 密集高阶幅相信号盲解调

传统基于星座图识别算法主要是消除频偏和噪声干扰等对星座图的影响，由于目标信号中包含5种调制方式，需在信号分离后，用多个对应接收机进行解调得到较为理想的星座图，这就大幅度提高了实际盲侦查解调时的计算复杂度。本文提出的高阶幅相信号盲解调算法先采用快速傅里叶变换(Fast Fourier Transform，FFT)粗估计信号载频[8]，再用频域峰值检测算法估计带宽[9]，低通滤波得到非时域混合的信号；然后通过位同步来消除收发端延迟和时钟偏移；最后利用盲高阶幅相锁相环路完成载波同步[10]。下变频低通滤波后被分离出来的第k个信号的第n个采样点表示为：

sk(n)=Ik(n)cos(ωckn+φk)-Qk(n)sin(ωckn+φk)+n0(n)

(2)

本文设计的盲数字接收机主要体现在载波同步环路中，不考虑噪声的影响，输入信号分别与本地振荡cos(ωckn+φ0)相乘，滤除高频分量后得到的同相正交支路Sik(n)和Sqk(n)分别为：

(3)

(4)

式中，Δφk=φ0-φk为本地振荡与载波信号间的相位差。

其中载波同步的鉴相部分采用的是高阶幅相信号盲鉴相器，鉴相方程为：

(5)

式中，sign(x)为符号函数。

当Δφk≪π/4时，sinΔφk≈0，cosΔφk≈1，将式(3)、式(4)代入式(5)，得到鉴相过程：

(6)

此时，鉴相器输出只与相位误差Δφk成正比，与输入信号幅度无关，环路稳定后误差Δφk将逐步振荡趋近于0，最终趋向锁定状态。通过以上分析可知，本文设计的盲接收机适用于所有目标信号。

2 基于星座图轨迹高阶幅相信号识别算法

2.1 星座图幅值曲线曲率分布

在密集高阶幅相信号环境下，相邻信号的频谱干扰降低了参数估计的精度，使得滤波后的信号存在有噪声分量，导致接收机无法实现理想解调的效果。解调信号星座图则因为存在一定频偏而发生旋转，呈现以原点为中心、幅度为半径的同心圆，其星座图有几种幅度，就呈现几个同心圆。传统基于星座图幅度信息的识别算法易受噪声和干扰影响，在低信噪比和干扰下，星座点分布较为分散，幅度信息区分度变小，性能下降[11]。本文算法将星座图幅值曲率分布与星座图独有的轨迹信息结合起来作为识别特征统计量，其目标信号星座图结构如表1所示。

表1 各幅相信号星座图结构

设xk(n)为第k个信号解调输出的第n个数据的星座点值，则有：

(7)

(8)

式中，D′k(n)为该点的一阶差分，D″k(n)为该点的二阶差分。在信息码元个数为400，信噪比为12 dB时，得到各信号曲率分布如图1所示。

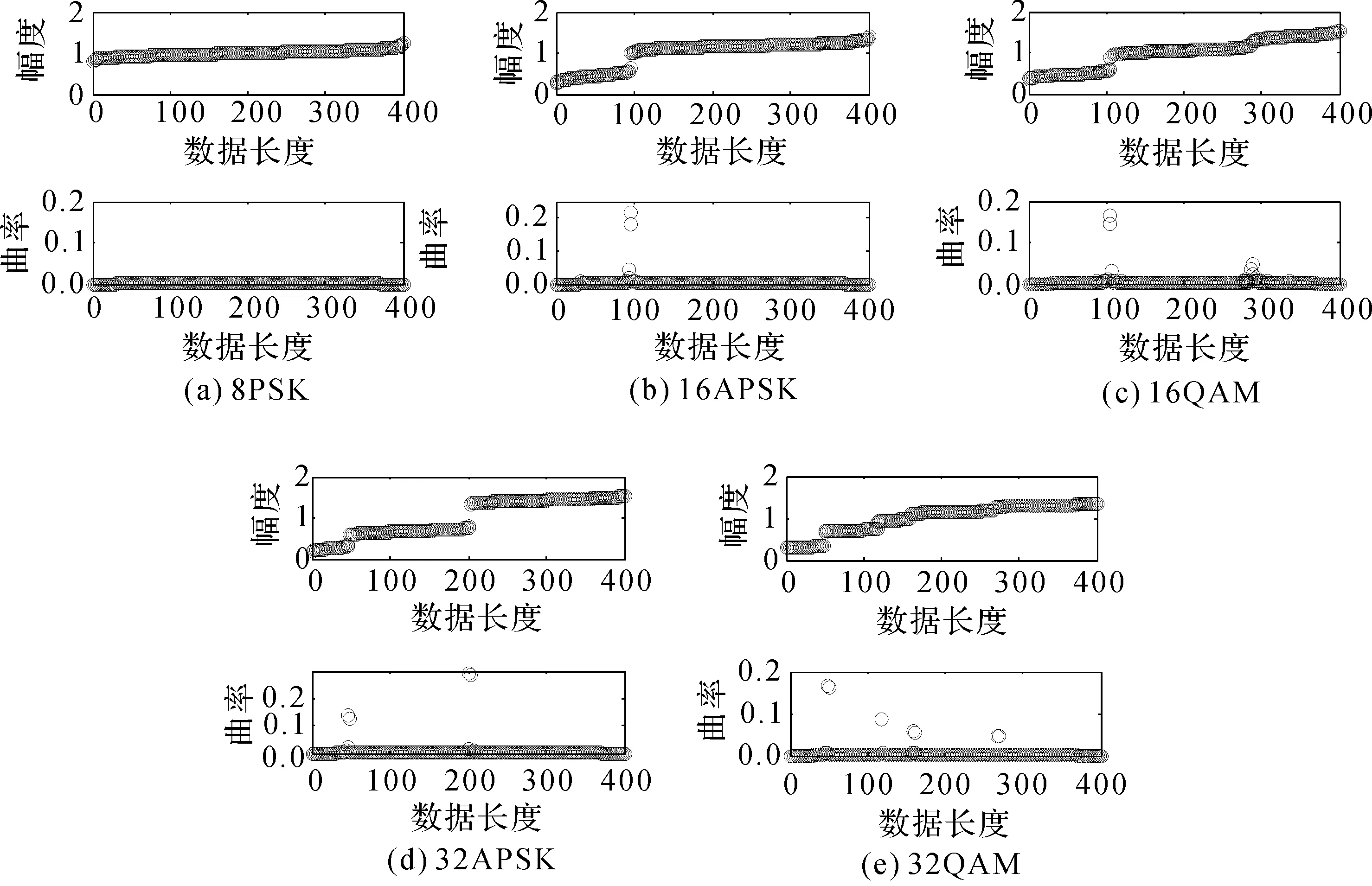
图1 密集信号环境下，不同信号的幅值分布曲线及其曲率图

从图1和式(8)可以看出，当幅度数据从小变大时，其幅值分布图中会出现一次明显的跳变，同时对应的曲率图Ck(n)也会出现一个峰值，即当该信号星座图有P0种不同幅度时，其曲率图中会对应出现P=P0-1个峰值。采用幅值分布曲线的曲率展现了星座图二阶导结构，更能体现出不同信号间星座图幅值分布的差异，同时其曲率峰值所在数据位置反映了各信号星座图特有的轨迹结构。

2.2 星座图轨迹特征提取

记分布在每个同心圆上的星座点个数为ni,i=1,…,P0，在信息码元个数N足够大的情况下，每个星座点上携带的信息码元个数基本一致，第m次幅度跳变时对应的数据位置Lm为：

(9)

式中，N为信息码元个数，M为信号进制数，P0为星座图同心圆个数，将表1数据代入式(9)，得到信号的轨迹特征如表2所示。

表2 不同信号的轨迹特征

从表2中可以看出，5种目标信号其曲率峰值可能会出现的跳变位置Lm总计有5个，即Lm∈{N/8,N/4,3N/8,N/2,3N/4}。且各信号的曲率峰值个数和曲率峰值出现的位置体现了各信号星座图的二阶导结构和不同的轨迹结构，说明以该结构为分类基础的调制识别算法受噪声影响更小。

由于存在噪声时星座点分散在圆环周围，造成各点幅度差异较小，其幅值分布曲率图中峰值点附近会存在许多干扰数据，因此选择统计其曲率分布Ck(n)中n=Lm时，这5个点附近共Y个数据的方差作为特征参数，第k个信号的第i个跳变点的特征参数为Vi,k(i,k=1,…,5)，表达式如下：

(10)

(11)

利用式(10)、式(11)进行统计，得到特征参数集合Vi,k(i,k=1,…,5)，用于判断信号幅度分布曲线的曲率在该点处是否有峰值。对应设置第i个跳变点的门限Ti(i=1,…,5)进行判别，判定规则：

(12)

以V1,k(k=1,…,5)为例，N=400时，每个信噪比下统计500次数据的均值，得到V1,k(k=1,…,5)随信噪比变化曲线如图2所示。记8PSK，16APSK，16QAM，32APSK，32QAM信号依次为第1，…，5个目标信号，n=N/8(第1个跳变点)处特征参数门限为：

(13)

式中，V1,k(k=1,…,5)为500次统计数据的均值。

由表2数据可知，在n=N/8处仅32APSK、32QAM星座图幅值曲率存在有峰值。从图2可以看出，32APSK，32QAM信号的特征参数V1,4，V1,5随信噪比增大而明显增大，其余信号则是随之减小，差异明显，这与表2中轨迹特征一致，证明利用V1,k判别n=N/8点处是否存在幅值跳变的正确性。以此类推，根据各信号在5个跳变点处的仿真结果设置对应门限Ti(i=1,…,5)进行判别，根据判别情况统计各幅相调制信号的幅值曲率图中出现峰值的个数P，以及幅值跳变点位置情况。

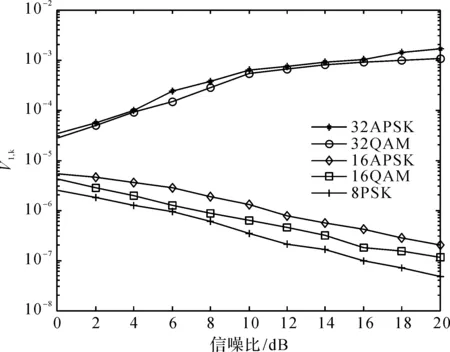
图2 特征参数V1,k随信噪比变化的曲线

2.3 基于星座轨迹图的调制方式识别算法

本文所提识别算法的主要流程如下：

(1)通过高阶幅相信号盲数字接收机对接收信号进行解调，得到非理想解调的星座图；

(2)对星座点幅值作归一化处理；

(3)用2.2节方法计算特征参数Vi,k(i,k=1,…,5)，设置合理门限Ti(i=1,…,5)判决得到曲率峰值个数P；

(4)将得到的特征参数值与表2中信号的轨迹特征一一对应来区分目标信号。

3 仿真分析

为验证文中所提算法的有效性，通过软件仿真统计出了该算法在不同情况的识别率。待识别密集调制样式集合为{8PSK，16APSK，16QAM，32APSK，32QAM}，信号参数设置为：基带信号序列随机产生，符号速率为1M Baud/s，采样频率为100 MHz，背景加性噪声为高斯白噪声，信息码元数N=500。8PSK幅度A=2；16APSK半径R1=1.00，R2=2.70；32APSK半径R1=1.00，R2=2.70，R3=5.71；16QAM幅度A=1,3；32QAM幅度A=1,3,5。文献[7]提出的基于星座图幅值分布信息的自适应模板匹配识别算法，抗频偏性强，识别性能较好，因此选择本文算法和文献[7]算法进行对比。

3.1 信噪比对识别性能的影响

图3 本文算法与文献[7]算法性能随信噪比变化曲线对比图

混合信号的信噪比为4～20 dB，每个信噪比下仿真进行10 000次蒙特卡洛实验，统计其正确识别概率，结果如图3所示。

由图3可以看出，本文算法在信噪比为9 dB时信号识别率均到90%以上，而文献[7]算法需在信噪比为11 dB时才能达到该性能。由于QAM信号幅值种数较多且数值相近，且受噪声影响星座点分布较为分散，导致QAM信号幅值分布曲线与理论模板差异大，易与APSK模板匹配成功，但对于本文算法所用幅值曲率与轨迹结合的特征受其影响较小，因此识别性能更优。

文献[7]通过计算出信号的实际幅度分布模板与各理论模板间的匹配误差，判定误差最小的模板对应识别成其调制样式，整体计算量大、复杂度高。而本文算法提取的特征参数即星座图幅值分布曲线曲率的峰值个数与峰值所在数据长度，计算简单，因此本文算法复杂度低于文献[7]算法。

3.2 干信比对识别性能的影响

目标信号的信噪比为12 dB，目标信号系数为1，干信比(干扰信号相对目标信号放大倍数)为1.0～4.5，每个干信比下仿真进行10 000次蒙特卡洛实验，统计其正确识别概率，结果如图4所示。

图4 本文算法与文献[7]算法性能随干信比变化曲线对比图

由图4可以看出，随着干信比的持续增大，对比算法性能快速下降，当放大倍数为2时，本文算法中8PSK，16APSK，32APSK信号的识别率能达90%，而对比算法无法达到该性能。综上表明，本文算法可有效地抗干扰。

3.3 码元数N对识别性能的影响

混合信号的信噪比为12 dB，信息码元个数N为40～400，步进为40，每个长度下仿真进行10 000次蒙特卡洛实验，统计其正确识别概率，得到仿真结果如图5所示。

图5 本文算法性能随信息码元个数N的变化曲线

从图5中可以看出，当N>200时，信号平均识别率达到90%以上。当N取值减小，分散到各个星座点上的码元数减少，导致相邻跳变点间的间隔变短，造成的数据混叠降低了识别精度。因此要使幅度分布的精度高就需要较多的信息码元，一般取长度为360个以上码元时比较合适。

4 结束语

本文针对密集高阶幅相信号8PSK，16APSK，16QAM，32APSK，32QAM的识别问题，提出基于高阶幅相盲接收机的解调信号星座轨迹图的调制识别算法。算法能有效抗频偏和噪声，复杂度低且性能优良，适于工程应用。但是，对于阶数更高、星座图结构更复杂的信号，本文算法难以适应，有待进一步改进和研究。