问题引领，在变式中学习几何模型

马园园

【摘要】在初中階段的数学教学中，几何图形的学习是非常重要的.它可以培养学生的逻辑思维能力、推理能力和论证能力.然而，几何严密的逻辑性使不少学生感到很难学.结合学生在学习几何时遇到的问题，本文探讨了如何在变式中进行解题教学，引导学生进行思维的发散和收敛，通过思维可视化解决几何书写的难题.

【关键词】几何图形教学;思维多样;思维可视化

一、问题提出

初一学生在学习“平面图形的认识”时，接触到了分类、转化、类比、归纳等常见的数学思想方法.在教授章节复习课时，为了让学生回顾、思考本章所学的知识及思想方法，我设计了这样一道例题：

已知下列三幅图中，AB∥CD，探索∠A、∠C和∠E之间的数量关系.

我的教学预设是：期望学生在研究图1时利用“转化”思想，然后模仿图1的辅助线作法，在图2、图3中“过点E作辅助线MN，使MN ∥AB”，从而解决问题.但在实际课堂教学中，学生的思维触角延伸到了多个方向，运用多种方法解决了问题，这一过程促使我对几何教学进行了反思.

二、教学片段回顾

1.多种解法，顺势追问

已知下列三幅图中，AB∥CD，探索∠A、∠C和∠E之间的数量关系.

生1：如图1，过点E作辅助线MN，使得MN ∥AB，进而得到∠A=∠AEM，∠C=∠MEC.∠AEC=∠AEM +∠MEC=∠A+∠C.

师：∠A和∠C可看成什么？它们怎样和∠AEC产生联系？

生1：∠A和∠C可看成∠AEM和∠MEC的内错角，通过内错角相等，得到∠A、∠C和∠AEC的关系.

生2：如图4，连接AC，∵AB∥CD，∴∠BAC+∠ACD=180°，即∠1+∠2+∠3+∠4=180°.又∵∠2+∠3+∠E=180°，∴∠1+∠4=∠E.

师：∠A和∠C可看成什么？它们怎样和∠AEC产生联系？

生2：∠A和∠C可分别看成同旁内角的一部分，通过三角形的内角和等于180°，得到∠A、∠C和∠AEC的关系.

生3：如图5，延长AE交CD于点F.∵AB∥CD，∴∠A=∠AFC，∴∠AEC=∠C +∠AFC=∠C +∠A.

师：比较一下，这几种解法你更喜欢哪一种？这三种解法有什么联系？

生4：这几种解法都是把要研究的角集中在一起.

师：我们通过平行线的性质将三个目标角集中在同一个顶点或同一个三角形内，化分散为集中，从而解决问题.

2.预设之外，寻找联系

已知图2中，AB∥CD，探索∠A、∠C和∠E之间的数量关系.

生1：如图6，∵AB∥CD，∴∠1=∠A.∵∠1=∠C +∠E，∴∠A=∠C +∠E.

师：除了用三角形外角的性质，有没有其他解答方法？回顾图1，我们通过构造平行线将∠E转化为∠A+∠C，你能用这种解法解决图2的问题吗？

生2：如图7，过点E作AB∥MN，得到∠AEM=∠A.易证CD∥MN，得到∠C=∠CEM.∠A=∠AEM=∠AEC +∠CEM=∠AEC +∠C.

师：图2和图1的区别在于点E的位置不同，但是解题思路是相似的，所以我们在平时解决一类问题时要注意寻找问题之间的联系和方法的迁移.

3.模型应用，解决问题

已知图3中，AB∥CD，探索∠A、∠C和∠E之间的数量关系.

大多数学生非常顺利地解决了图3的问题.课堂测试显示，全班41人中约30人采用了“过点E作辅助线”.我询问学生是否有不同解法.几名学生受张同学解决图1思路的启发，利用三角形内角和定理或多边形内角和定理解决了图3的问题，辅助线作法如下：

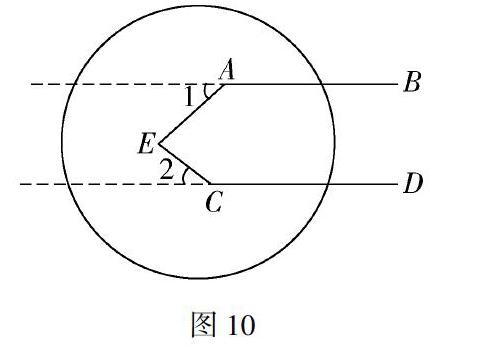
我正准备做小结，孙同学非常激动地举手：“老师，我和他们的方法都不一样，我能把图3变成图1！”我和其他学生在那一瞬间都愣住了.孙同学走向黑板，在图3上延长BA、DC，并在图3上画了一个圆，如图10所示：

孙同学说：“我圈出来的部分向右翻折就变成了图1，所以可以直接用图1的结论∠E=∠1+∠2，又因为∠1=180°-∠BAE，∠2=180°-∠ECD，所以得到∠E=360°-∠BAE-∠ECD.”我和其他同学恍然大悟，无不称妙！孙同学的数学素养非常不错，能运用模型思想.我点评：“孙同学在图3中分离出了图1的模型，然后直接运用图1的结论，这就是模型思想.”

4.总结策略、落实书写

师：这三道题我们都构造了辅助线来解决问题，你能总结一下有哪些构造辅助线的方法吗？

生1：作已知直线的平行线和连接线段.

生2：还有延长线段.

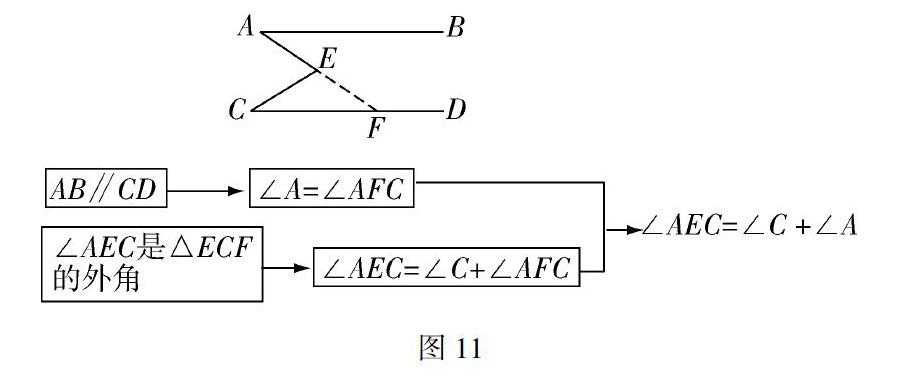
师：我们借助思维导图来梳理一下思路，以第二题为例.

教师板书：

学生根据图11写出解题过程.

师：思维导图对你写解题过程有什么帮助？

生3：思路更清晰，思维导图很直观.

师：思维导图非常直观，让思维可视化.

三、几何解题教学中的思考与实践

1.应多设计变式题组

在设计例题时，若多以题组的方式呈现，或设计几个有关联的几个小题，或设计条件发生变化的几个小题，或设计解题方法类似的几个小题，则能给学生“整体”的感觉.教学时，教师应引导学生前后联系，类比解题方法.

教师应鼓励学生敢于联想，一题多解.在研究图1时，给出的辅助线使学生思考的路径变得单一，不利于学生发散思维.张同学这样的学生是少见的，他能放着现成的提示不用，坚持不同的解法.在研究图3时，一些学生的思维已经活化，解题方法多样.

2.应多总结基本模型

在做题中积累经验，总结一类题的解题方法，注重基本模型的提取.孙同学在解决图3时分离出图1的模型的做法体现了较高的思维品质，教师在教学中应强化学生应用模型的能力，提升学生的思维品质.

3.应接纳思维的差异性和多样性

在几何解题教学中，教师应该关注学生怎么想、为什么这样想、怎样才能想到.从条件到结论，思考途径的产生和优化是几何解题教学的价值所在.教师应该在实际学情的基础上及时调整预设目标，接纳学生的不同思维成果，引导学生比较解法和寻找最优解法，让学生的思维经历发散和收敛的过程.教师的预设绝不能强加给学生，教师也不能替代学生思考.

4.应该借助思维导图让思维可视化

解决数学问题的一般步骤是：整理条件、制订计划、执行计划、回顾反馈.教师可引导学生梳理条件，然后考虑从每个条件出发可以得到什么新结论，条件组合后可以得到什么新结论，这些新结论和目标结论之间有什么关系，怎样构建与目标的关系等.

从条件出发，从已知到可知，由未知找需知，不断在已知和未知之间寻找联系.思维导图体现了思维的发散和收敛.先打开思维，从一到多;再收敛思维，从多到一.

学生在可视化的思维导图的帮助下形成书写逻辑，让思路更加清晰有序.在长期训练下，学生的几何解题思路逐渐清晰，并且学生在发散和收敛思维的过程中自觉优化解题思路.

基于上述反思，课后我设计了这样的题目：

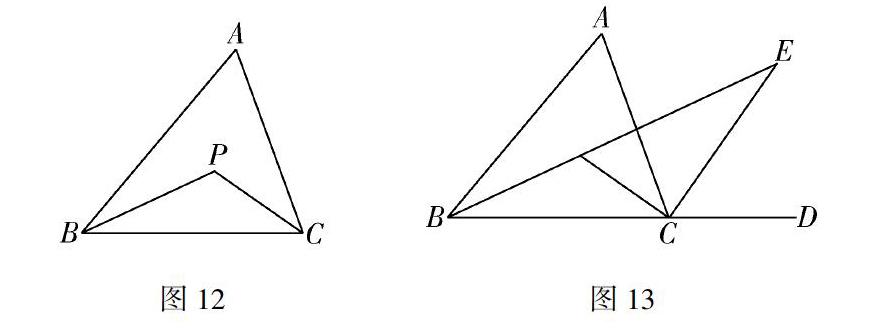
（1）如图12，在△ABC中，如果BP、CP分别平分∠ABC、∠ACB，易知∠A与∠BPC的数量关系是∠BPC=90°+12∠A.

（2）请利用（1）中的结论解决以下问题：

如图13，在△ABC中，如果BE平分∠ABC，那么CE平分△ABC的外角∠ACD.探索∠A与∠E的数量关系并说明理由.

【参考文献】

[1]金盼.变式在数学教学中的应用[J].初中数学教与学，2019（14）：15-16.