基于拓展电压矢量集合的永磁同步电机无差拍控制
2021-04-06李耀华周逸凡赵承辉秦玉贵
李耀华,周逸凡,赵承辉,秦玉贵
(长安大学 汽车学院,西安 710064)
0 引 言
永磁同步电机直接转矩控制根据滞环比较器得到转矩与磁链增减信号,通过查表方式确定输出唯一电压矢量,控制简单,响应速度快[1-3]。但受开关表电压矢量数量限制,且每个采样周期只作用一个基本电压矢量,直接转矩控制的转矩与磁链脉动较大。为了减小脉动,国内外学者通过改进开关表[4]、调节占空比[5]、空间矢量调制技术[6]等对直接转矩控制进行优化。
基于系统离散模型的无差拍(以下简称DB)控制令下一时刻的转矩与磁链的预测值与参考值相等,理论上可以使系统在一个控制周期内的转矩误差与磁链误差为零[7]。传统DB控制实时求解较为复杂的一元二次方程,并需要对方程的根进行判断,计算量较大。在磁链与转矩变化较大时,求解出的电压矢量超出逆变器的输出电压限制,无法通过空间矢量调制输出,需要进一步设计电压矢量选择策略,增加了系统的复杂程度[8-9]。文献[10-12]通过模型预测控制,输出与DB控制理想电压矢量最接近的基本电压矢量,并将实际参与成本函数计算的基本电压矢量进行精简,计算量减少,但其性能受到基本电压矢量个数限制。文献[13]提出一种无需模型预测控制,仅通过理想电压矢量幅值判断确定施加电压矢量的方法,简化了选择方法,但仍仅输出基本电压矢量。文献[14-15]通过改变占空比,将备选电压矢量数目进行拓展,以减少理想电压矢量与实际施加电压矢量之间的误差,但仍涉及成本函数的计算,计算量较大。
为了降低直接转矩控制的转矩脉动,本文提出了永磁同步电机磁链与转矩DB控制,建立了磁链与转矩的变化量简化计算模型,并验证了简化模型的可行性,从而推导出实现磁链和转矩DB控制的理想输出电压矢量计算方程。为了简化DB控制下理想电压矢量的实现,提出通过理想电压矢量角度和幅值简化选择7个基本电压矢量的方法(DB-MPC-7),无需成本函数计算。为了减小理想电压矢量与实际输出电压矢量之间的误差,进一步改善控制效果,提出一种从角度和幅值对备选电压矢量进行拓展的方法(DB-MPC-36r),将备选电压矢量角度拓展至36个,输出电压矢量幅值可为线性调制范围内任意值。该方法通过查表方式即可实现,无需空间矢量调制计算,简单易行。仿真验证了永磁同步电机磁链和转矩DB控制的可行性。相较于DB-MPC-7,DB-MPC-36r可显著减小转矩脉动,降低电流谐波含量,但平均开关频率有所增大。
1 永磁同步电机磁链与转矩变化量简化计算模型
忽略定子电阻压降,由电压矢量Vs引起的PMSM定子磁链运动如图1所示。
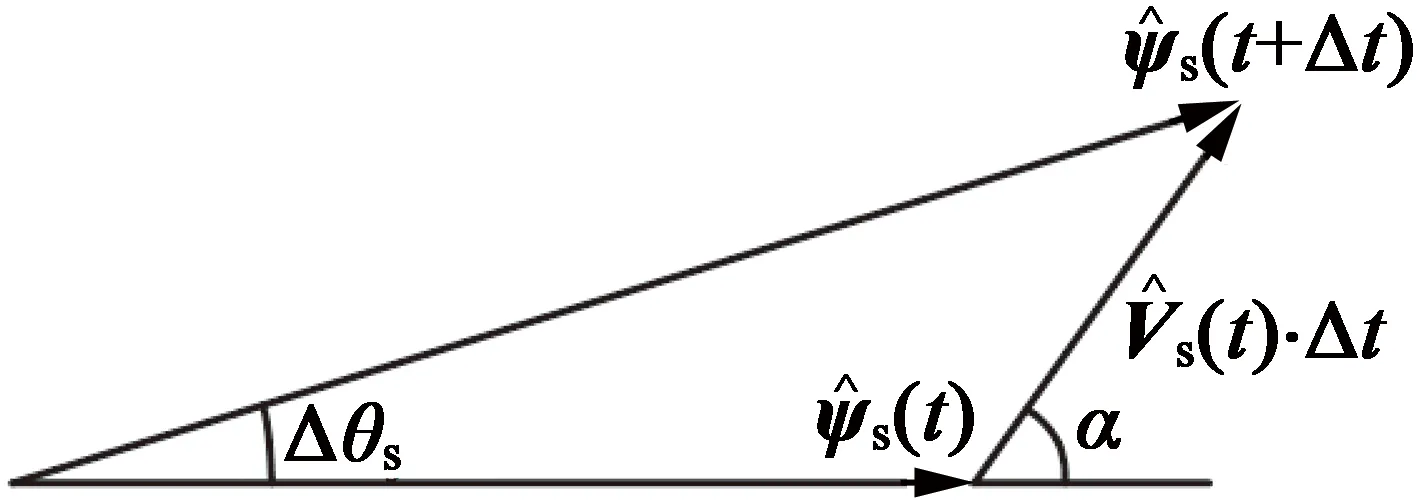
图1 定子磁链运动
由图1可知,第(t+Δt)时刻的定子磁链幅值如下式:
(1)
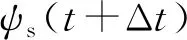
在采样周期很小的情况下,转子磁链运动较小,其对转矩角的影响可以忽略不计。由图1可知,施加电压矢量引起的转矩角变化如下式:
(2)
由式(2)可知,第(t+Δt)时刻的转矩角如下式:
(3)
永磁同步电机转矩方程:
(4)
式中:p,ψf,Ld和Lq分别为电机极对数,永磁体磁链,d轴和q轴电感。当k=0时,Ld=Lq,式(4)即为表面式永磁同步电机转矩方程。
由式(1)~式(4)可得下一时刻的永磁同步电机转矩方程:

k(t+Δt)sinδ(t+Δt)cosδ(t+Δt)]
(5)
由k的定义可知,下一时刻k值如下:
(6)
将式(1)、式(3)和式(6)代入至式(5),可得下一时刻的永磁同步电机转矩表达式:
(1+q2+2qcosα)k(t)sin[δ(t)+
(7)
根据式(1)和式(7),电压矢量作用一个采样周期后磁链和转矩变化量如下式:
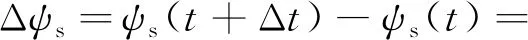
(8)
ΔTe=Te(t+Δt)-Te(t)=
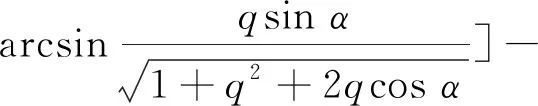
(1+q2+2qcosα)·k(t)·sin[δ(t)+

sinδ(t)+k(t)·sinδ(t)cosδ(t)}
(9)
为了减少DB控制的计算量,对式(1)和式(7)进行简化,可得永磁同步电机下一时刻磁链与转矩简化计算模型[16-17]:
(10)

ksinδ(t)cosδ(t)+qsin[α+δ(t)]-
k·qsin[α+2δ(t)]}
(11)
由式(10)~式(11)可得,施加电压矢量引起的定子磁链幅值和转矩变化量简化计算模型:
(12)
ΔTe_sim=Te(t+Δt)sim-Te(t)=
(13)
为了验证定子磁链幅值和转矩变化量简化计算模型的有效性,定义施加电压矢量引起的定子磁链幅值和转矩变化量简化模型与常规模型的相对误差率绝对值:
(14)
(15)
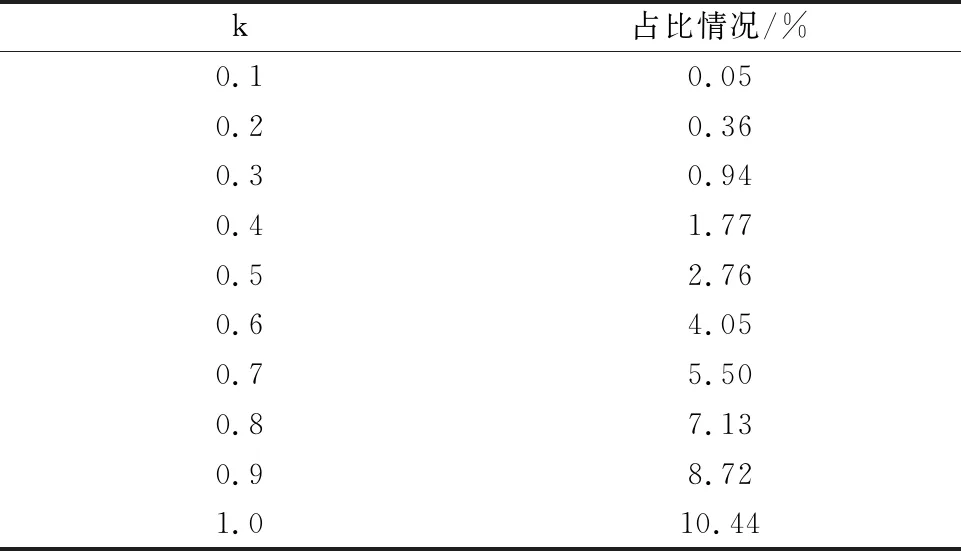
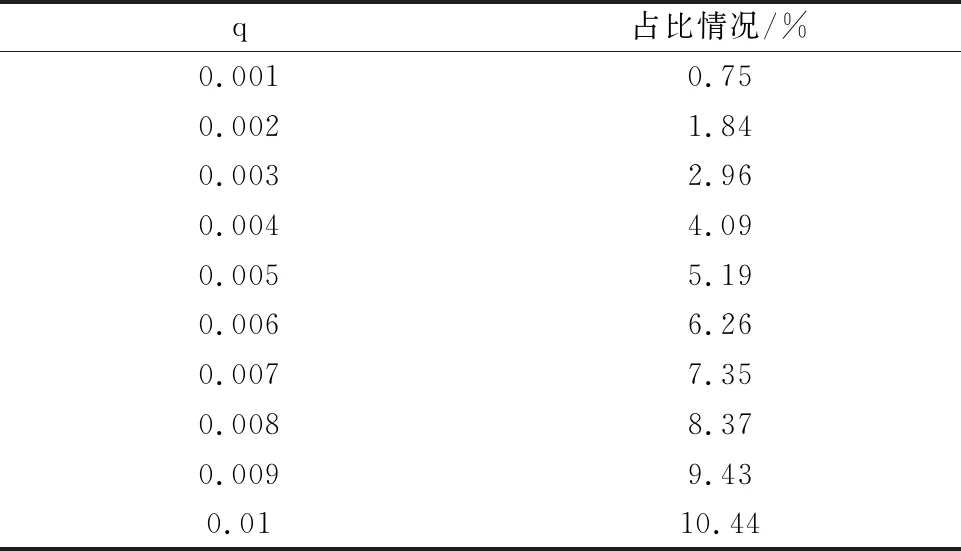
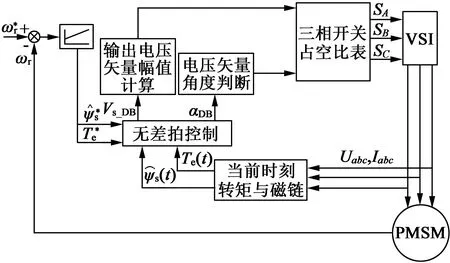
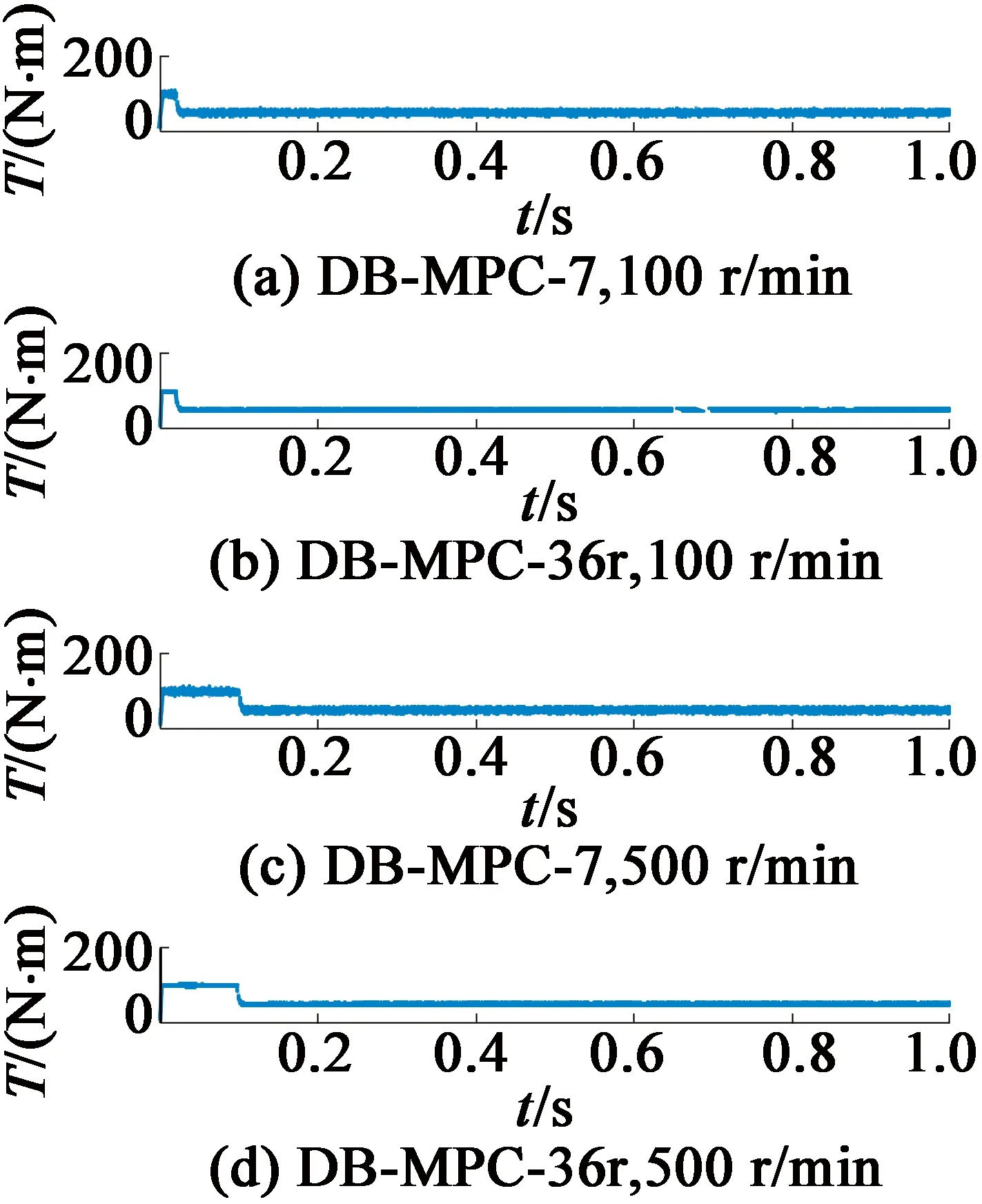
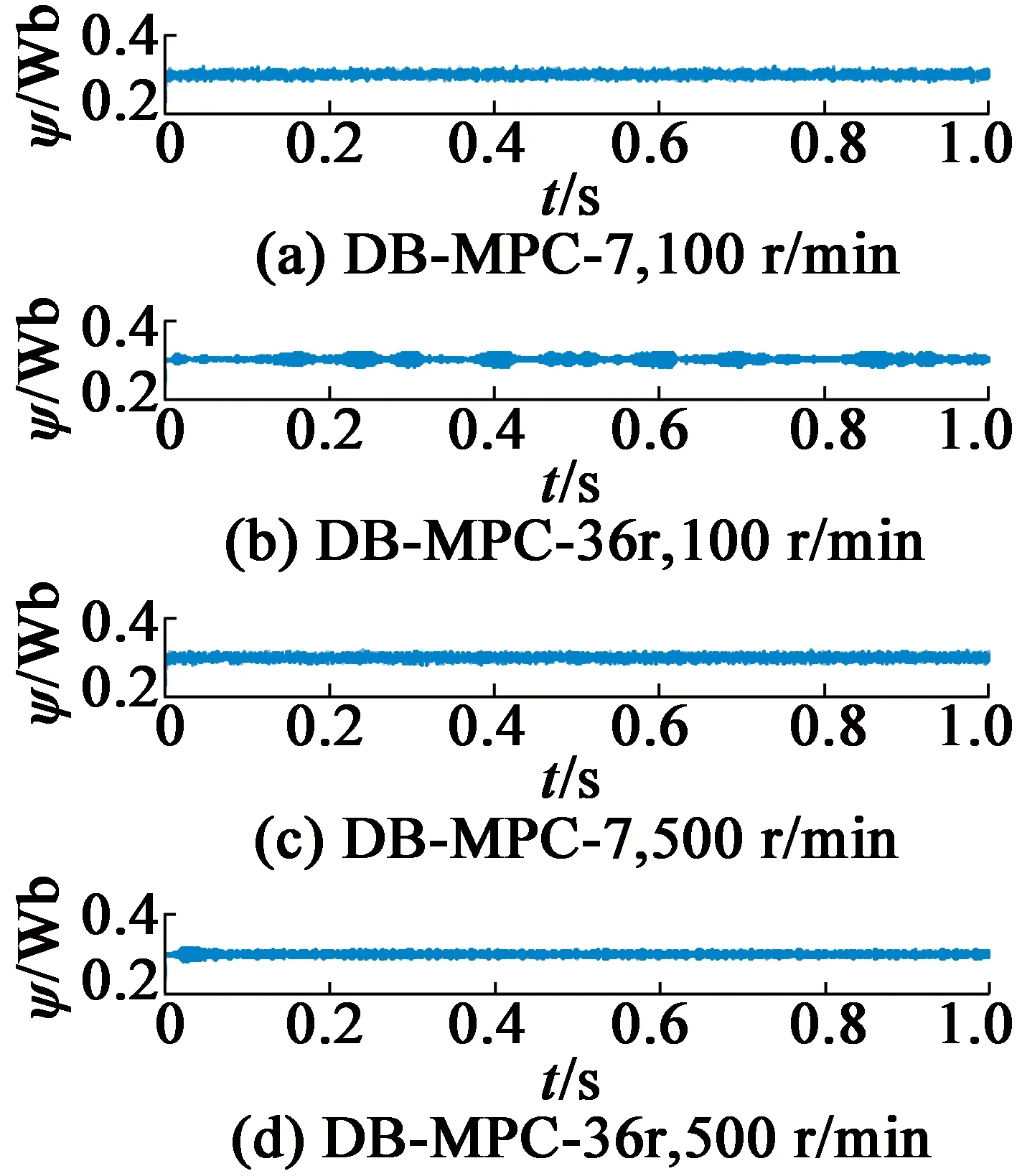
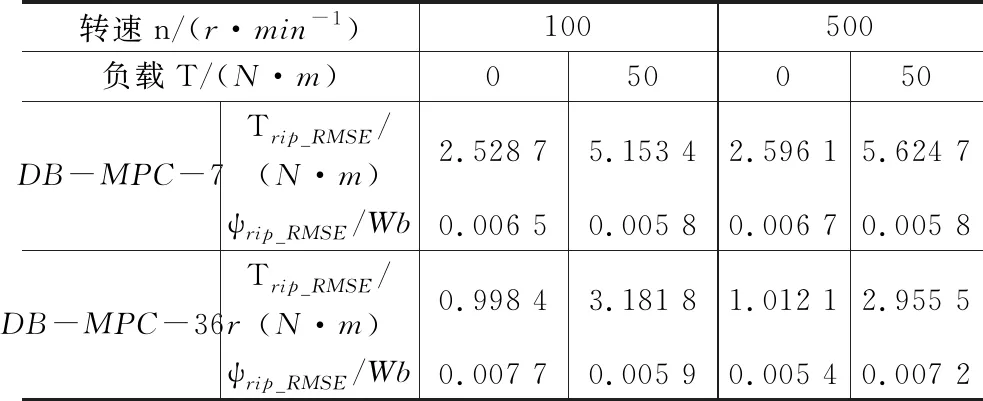
当0 图2 磁链变化量简化计算模型与常规模型的相对误差 经统计,仅当α接近90°和270°时,即分母过零点区域,误差率较高,约占总数据的6%,其余94%区域的误差率数据绝对值小于5%。统计结果表明:采用简化模型代替常规模型来预测磁链变化量基本可行,即式(16)成立。 (16) 当k=1,q=0.01,0<α≤360°,0<δ≤120°,转矩变化量简化计算模型与常规模型的相对误差率如图3所示。 图3 转矩变化量简化计算模型与常规模型的相对误差 经统计,仅在分母过零点区域,转矩变化量误差率较高。统计表明,简化模型与常规模型误差率绝对值小于5%的情况,占总数据约90%。 不同转矩角下,转矩变化量误差率绝对值大于5%的数据占比情况,如表1所示。由表1可知,转矩角较小时,转矩变化量误差率大的数据较多。 表1 不同转矩角下,转矩变化误差率绝对值大于5%数据占比 当q=0.01,0<α≤360°,0<δ≤120°,不同k值下,转矩变化量误差率绝对值大于5%的数据占比情况如表2所示。表2表明,仅当k值较大时,转矩变化量误差率大的数据较多。 表2 不同k值下,转矩变化误差率绝对值大于5%数据占比 当k=1,0<α≤360°,0<δ<δmax,不同q值下,转矩变化量误差率绝对值大于5%的数据占比情况如表3所示。表3表明,仅当q值较大时,转矩变化量误差率大的数据较多。 表3 不同q值下,转矩变化误差率绝对值大于5%数据占比 由表1~表3可知:仅当k较大、q较大及转矩角较小时,转矩变化量误差率大的数据较多,且仅限于分母过零点附近区域。因此,采用简化模型代替常规模型来预测转矩变化量基本可行,即式(17)成立: ΔTe_sim≈ΔTe (17) 根据磁链与转矩无差拍控制思想,第(t+Δt)时刻永磁同步电机的磁链与转矩值应等于第(t+Δt)时刻的参考值,即: (18) (19) 由于采样频率较高,第(t+Δt)时刻的磁链和转矩参考值可近似等于第t时刻的参考值: (20) (21) 由式(18)~式(21)可知,满足DB控制的理想磁链与转矩变化量如下式: (22) (23) 由式(12)~式(14)、式(16)~式(17)可知,施加电压矢量一个采样周期后,磁链与转矩的变化量如下式: (24) k(t)sin[α+2δ(t)]}= k(t)sin[α+2δ(t)]} (25) 由式(24)可得: (26) 将式(26)代入式(25),变换可得: (27) 在磁链与转矩DB控制下,实际磁链与转矩的变化量与满足无差拍控制的理想磁链与转矩变化量相同,即式(28)~式(29)成立: (28) (29) 将式(22)和式(23)代入至式(27),则可求得令磁链与转矩在第(t+Δt)时刻满足DB控制的理想电压矢量角度αDB: (30) (31) 通过式(30)和式(31)求解得出第(t+Δt)时刻应施加的理想电压矢量的幅值和角度后,采用简化电压矢量选择方法,从基本电压矢量集合中选择最优电压矢量作为输出。基本电压矢量集合如下式: Vs∈{V0,V1,V2,V3,V4,V5,V6} (32) 式中:Vs为备选电压矢量,V0-V6为逆变器产生的7个基本电压矢量。当输出零电压矢量时,可以由上一时刻的开关状态选择开关次数较少的V0开关状态[18-20]。 传统模型预测控制需要遍历7个电压矢量[21],计算量较大。为了减少计算量,可根据静止坐标系下理想电压矢量角度,减少备选电压矢量,如式(33)所示。 (33) 将备选电压矢量集合缩小后,可无需成本函数计算,直接通过判断理想电压矢量幅值大小,确定是否选择非零电压矢量或零电压矢量。以备选电压矢量为V0和V1为例,如式(34)所示,若理想电压矢量幅值大于基本电压矢量幅值的一半,即Udc/3,则选择非零电压矢量;反之,选择零电压矢量。 (34) 将上文所述的简化电压矢量选择磁链和转矩无差拍控制系统,记为DB-MPC-7。DB-MPC-7的系统控制框图如图4所示。 图4 DB-MPC-7系统控制框图 由上文可知,DB-MPC-7选用7个基本电压矢量中的一个近似替代理想电压矢量,角度和幅值都受到较大限制,理想电压矢量与施加的电压矢量之间存在较大的误差,影响系统性能。因此,本文对备选电压矢量进行拓展,增大备选电压矢量数量,减小理想电压矢量与施加电压矢量间误差。 图5 [0°,60°]区间备选电压矢量 (35) 根据理想电压矢量的角度和幅值,DB控制最终输出电压矢量由式(36)确定: (36) 由于输出电压矢量的角度确定已知,在确定输出电压矢量后,可采用查表方式直接得到电压矢量相应占空比。以[0, 50°]区间为例,DB-MPC-36r控制下电压矢量对应的三相开关占空比如表4所示。 表4 DB-MPC-36r电压矢量三相开关占空比 图6 DB-MPC-36r系统控制框图 基于MATLAB/Simulink平台,搭建了永磁同步电机拓展电压矢量DB控制系统仿真模型,对DB-MPC-7和DB-MPC-36r进行对比验证。系统采样周期为1×10-4s。仿真用永磁同步电机参数如表5所示。 表5 仿真用永磁同步电机参数 为评价DB-MPC-7和DB-MPC-36r的稳态特性,设定参考转速为100r/min和500r/min,DB-MPC-7和DB-MPC-36r控制下的永磁同步电机系统分别在空载和负载条件(50N·m)由静止起动。永磁同步电机转矩和定子磁链幅值如图7~图10所示。 图7 不同转速下空载转矩 图8 不同转速,50 N·m 图9 不同转速下空载稳态磁链 图10 不同转速,50 N.m负载下稳态磁链 仿真结果验证了永磁同步电机磁链和转矩DB控制的可行性,采用DB-MPC-7和DB-MPC-36r均可实现永磁同步电机静态起动。 定义稳态下(0.1s~1s)转矩脉动均方根误差、磁链脉动均方根误差如式(37)~式(38)所示,其中n为采样总个数。 (37) (38) DB-MPC-7和DB-MPC-36r在不同负载和不同转速下的系统稳态转矩脉动以及稳态转矩磁链脉动如表6所示。 表6 不同控制策略下的稳态控制性能 由表6可知,相较于DB-MPC-7,在低速空载时,DB-MPC-36r降低转矩脉动60.5%,磁链脉动略有上升;低速加载时,DB-MPC-36r降低转矩脉动38.2%,磁链脉动基本相同。在高速空载时,DB-MPC-36r降低转矩脉动61.0%,磁链脉动也略有下降;高速加载时,DB-MPC-36r降低转矩脉动47.4%,磁链脉动略有上升。仿真结果表明DB-MPC-36r可较大幅度降低转矩脉动。 空载下,DB-MPC-7和DB-MPC-36r的定子磁链轨迹如图11所示。 (d) DB-MPC-36r,500 r/min 由图11可知,DB-MPC-7和DB-MPC-36r的磁链轨迹都接近圆形。相较于DB-MPC-7,DB-MPC-36r的磁链轨迹更加平滑。 (a) DB-MPC-7,100 r/min (b) DB-MPC-7,500 r/min (c) DB-MPC-36r,100 r/min 转速为500r/min且负载为50N·m下,DB-MPC-7和DB-MPC-36r稳态a相电流和电流总谐波含量(THD)如图12~图13所示。 (a) DB-MPC-7 (b) DB-MPC-36r (a) DB-MPC-7 (b) DB-MPC-36r 由图12~图13可知,相较于DB-MPC-7,DB-MPC-36r控制下的电流波形更加平滑,总谐波含量明显下降。 转速开环下,参考转矩在0.01s时由零阶跃至 50N·m,DB-MPC-7和DB-MPC-36r控制下转矩动态特性如图14所示。 图14 不同控制策略下转矩阶跃动态响应 由图14可知,DB-MPC-7动态响应速度略快于DB-MPC-36r。稳态下,DB-MPC-7转矩脉动明显大于DB-MPC-36r。 定义系统平均开关频率fave如下: (39) 式中:Nswitching为逆变器开关总次数;t为仿真总时长。 不同转速下,DB-MPC-7和DB-MPC-36r控制下的平均开关频率如图15所示。 图15 不同转速下DB-MPC-7和DB-MPC-36r的平均开关频率 由仿真结果可知,不同转速下DB-MPC-36r的平均开关频率均高于DB-MPC-7。这是因为一个采样周期内DB-MPC-7只作用一个基本电压矢量,且相邻采样周期作用的基本电压矢量可以相同,而DB-MPC-36r一个采样周期内作用2或3个基本电压矢量,且相邻采样周期施加的电压矢量基本不同。 本文对永磁同步电动机磁链与转矩变化量计算模型进行了简化,验证了简化模型的可行性。推导出满足磁链与转矩DB控制的理想电压矢量,提出简化选择7个基本电压矢量的方法(DB-MPC-7)及从角度和幅值对备选电压矢量进行拓展的方法(DB-MPC-36r)。前者使用逆变器生成的7个基本电压矢量,后者将备选电压矢量角度扩展至36个且幅值在线性调制范围内任意可调。通过仿真对比,得出结论如下: 1) 永磁同步电动机磁链与转矩DB控制可行,电机系统运行良好。 2)DB-MPC-7通过理想电压矢量角度和幅值确定施加的电压矢量,无需成本函数计算,省去传统模型预测控制计算。 3)DB-MPC-36r根据理想电压矢量角度和幅值通过查表方式生成角度更加丰富且幅值连续可变的电压矢量,从而减小施加电压矢量与理想电压矢量的误差,且无需空间矢量调制,简单易行。 4) 相较于DB-MPC-7,DB-MPC-36r可显著减小转矩脉动和电流谐波含量,动态响应基本相当,但平均开关频率有所增大。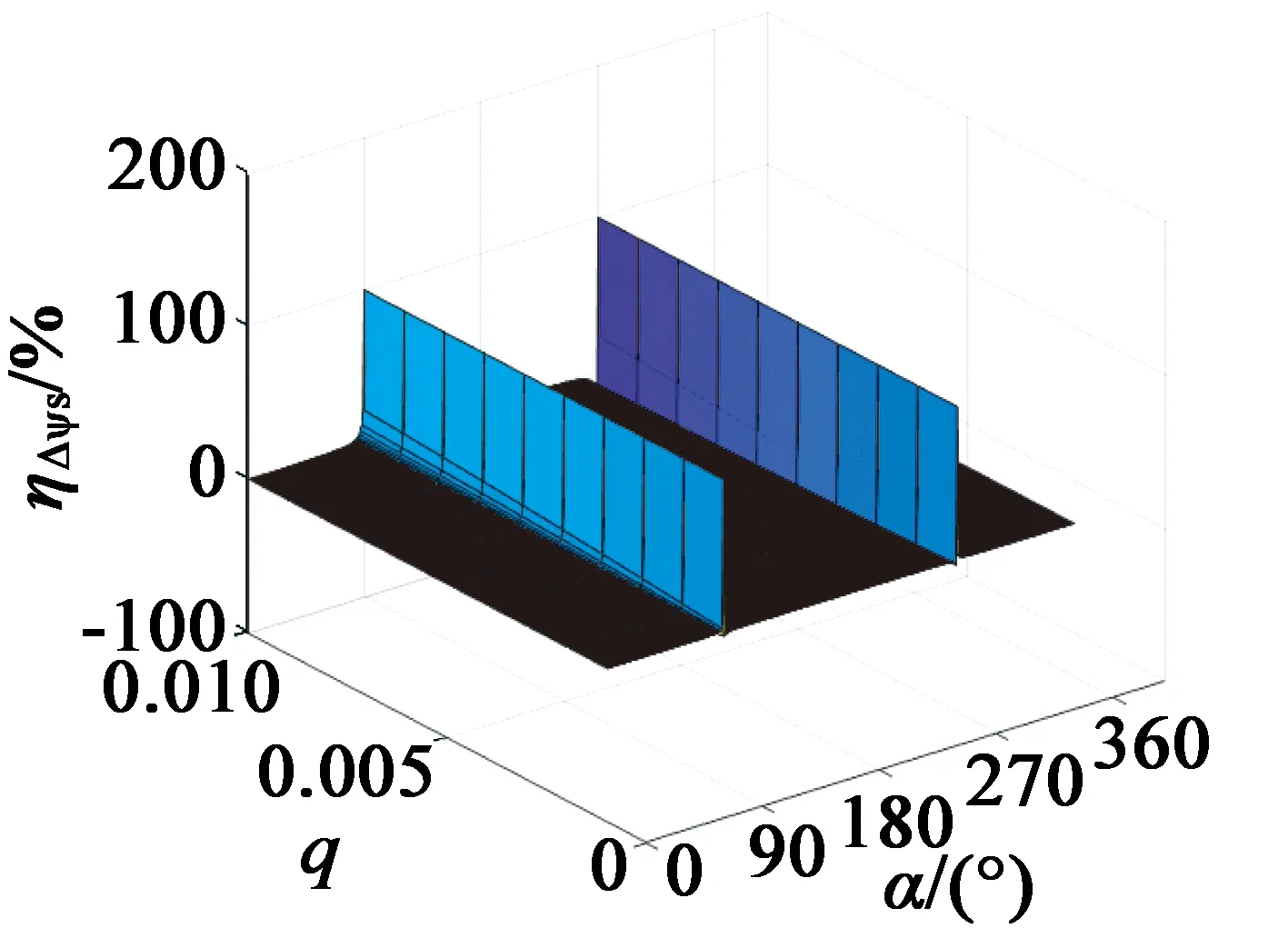


2 永磁同步电机磁链与转矩DB控制

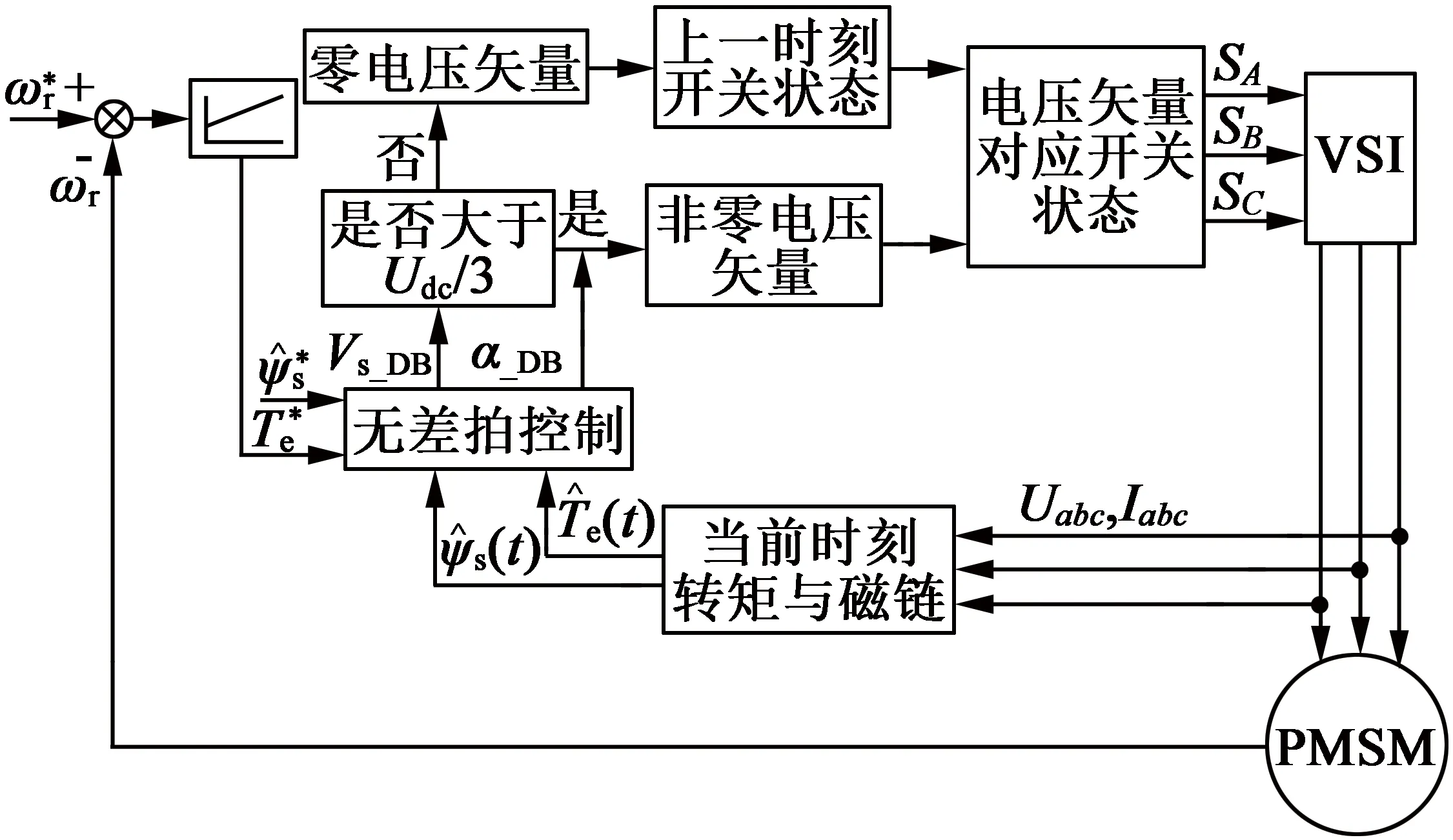
3 基于拓展电压矢量集合的磁链和转矩DB控制
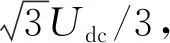

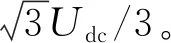


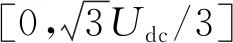
4 仿真对比

4.1 稳态特性










4.2 动态特性

4.3 平均开关频率

5 结 语
