基于有限公式法的永磁电机温升仿真实验教学平台与应用
2021-04-06朱高嘉李龙女
朱高嘉,李龙女
(天津工业大学 电工电能新技术天津市重点实验室,天津 300387)
永磁电机具有效率与功率密度高、高效区大、动态响应好的特点[1],在新能源交通、航空航天、智能制造等领域受到了广泛关注[2-3]。为了保证电机在长期运行中不会因为过高的温升而导致绝缘损坏[4]、轴承润滑油过度挥发[5]、永磁体工作状态下剩磁和矫顽力降低甚至不可逆退磁[1],需要研究和掌握其温升的准确分析方法。
采用数值计算可以得到电机温升的精确分布状态,是目前永磁电机发热与散热分析中最主要的手段。然而,基于有限差分法(finite difference method,FDM)、有限元法(finite element method,FEM)、有限体积法(finite volume method,FVM)等常规数值方法的离散过程需要进行复杂的数学变换[6],工程专业的本科生和低年级研究生掌握其核心机理的难度较大,进而难以从原理和方法的层面加深对永磁电机温度场数值计算的认识。有限公式法(cell method, CM)由意大利学者Tonti 于2001 年提出[7],通过对偶复型单元上物理方程的变换,直接得到代数、离散型控制方程组,其数学模型的物理意义清晰明确[8],便于学生通过实际工程案例的分析掌握其基本原理和分析方法。
本文从有限公式法的基本理论出发,探寻基于有限公式法的永磁电机温度场数学模型,分析其物理意义。搭建基于有限公式法的永磁电机三维温度场数值计算平台,从而为永磁电机设计类课程中温升分析与冷却设计提供有效教学条件。
1 有限公式法基本理论
有限公式法是一种代数型数值计算方法,其基本思想来源于Tonti 在物理定律直接代数表达的前期研究。有限公式法通过复型单元的原空间节点、单元线、单元面、单元体与映射空间单元体、单元面、单元线、节点间的对偶关系[8],可以将各类守恒方程的推导直接嵌套于单元剖分结构,实现代数、离散型控制方程的直接获取。有限公式法复型单元结构如图1 所示。
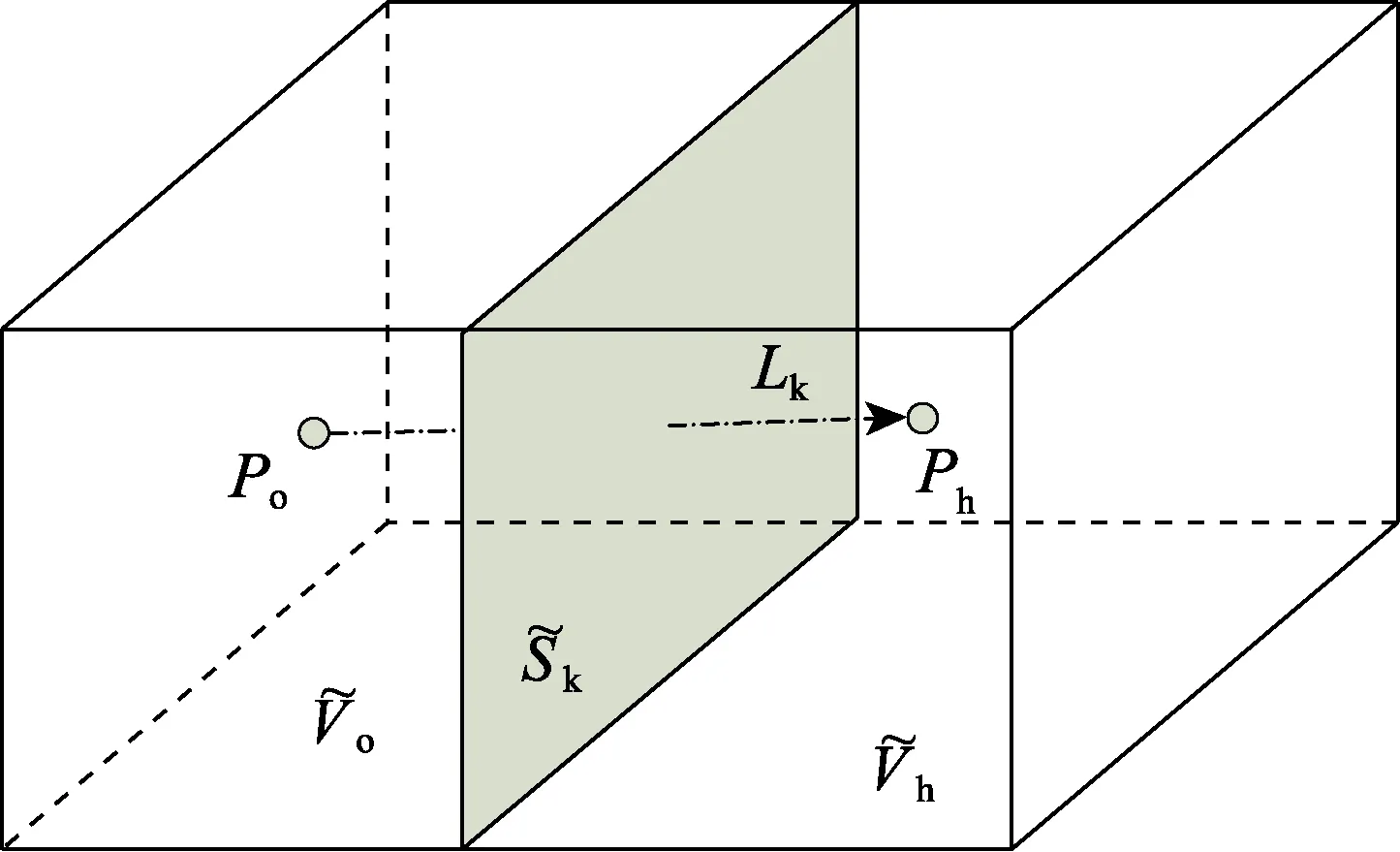
图1 基于有限公式法的复型单元结构
基于有限公式法的单元变换可综合为两类运算:①同一类单元不同维度间变换可转化为拓扑运算;②不同类型单元间对偶维度之间的变换可转化为本构运算。
分布形式、向量化的物理量的原空间拓扑运算可由3 类拓扑矩阵的左乘实现:①G为原空间由点(原空间零维)-线(原空间一维)拓扑矩阵;②C为原空间由线(原空间一维)-面(原空间二维)拓扑矩阵;③D为原空间由面(原空间二维)-体(原空间三维)拓扑矩阵。相应地,映射空间拓扑矩阵为:①为映射空间由点(映射空间零维)-线(映射空间一维)拓扑矩阵;②为映射空间由线(映射空间一维)-面(映射空间二维)拓扑矩阵;③为映射空间由面(映射空间二维)-体(映射空间三维)拓扑矩阵。如图1 所示,由原空间、映射空间单元间的对偶关系,有本构运算反映两套对偶单元间的物理变换,可通过左乘本构运算矩阵M实现[10]。
根据有限公式法的基本理论,将物理问题的物理量定义在原空间/映射空间的某一维度(如节点零维、单元线一维、单元面二维、单元体三维);通过左乘拓扑矩阵实现同一套空间内维度变换,得到定义在其他维度上的物理量;通过左乘本构矩阵,实现两套空间之间的变换,得到定义在其他空间的物理量。由于原空间-映射空间之间存在对偶关系,当初始物理量维度和变换终止物理量维度相同时,可得到符合计算要求的有限公式控制方程组,实现物理问题的有效数学建模。
2 基于有限公式法的电机温度场数学建模
由基于有限公式法的控制方程单元离散基本原理和传热学基本理论出发,可将电机温度场问题的有限公式变换过程表述如下:
(1)将“温升”定义在原空间单元节点(原空间0 维),通过拓扑矩阵G实现原空间节点(原空间零维)向单元线(原空间一维)的变换,得到原空间一维尺度单元线上的“温升差”。
(2)如图1 所示,映射空间单元面与原空间单元线对偶,通过本构矩阵M实现原空间单元线(原空间一维)向映射空间单元面(映射空间二维)的变换,得到映射空间二维尺度上的“热通量”。
(3)通过拓扑矩阵~D实现映射空间单元面(映射空间二维)向单元体(映射空间三维)的变换,得到映射空间三维尺度单元体上的“热功率散出”。
(4)通过前3 次变换,将原空间节点“温升”与映射空间单元体上的“热功率散出”相匹配,两者在空间上同样存在对偶关系,如图1 所示。
基于有限公式法的电机温度场变换过程可通过Tonti 图表示,如图2 所示。Tonti 图作为有限公式法的核心组件,可清晰、明确地表述物理量的变换过程,目前已在基于其他数值分析方法的电工装备多场耦合问题中得到应用和推广[11]。将之用于教学可帮助学生加深对理论和变换关系的认识。
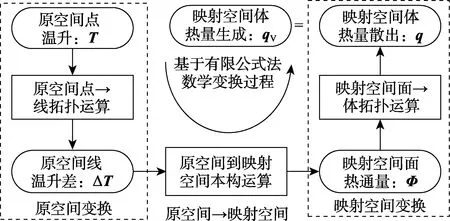
图2 基于Tonti 图的温度场数学变换
教学过程中,可结合变换过程和Tonti 图,讲解基于有限公式法的温度场数学模型:

式中:T为温升向量,K;qV为映射空间单元内生热,W。
3 永磁电机温升计算平台搭建
3.1 基本假设与边界条件
由式(1)所示基于有限公式法的电机温度场数学模型出发,强加边界条件,形成其定解问题。在电机温度场计算与分析中,为了在保证计算精度的同时降低总体求解计算量,一般需作出如下基本假设[12]:①根据电机的对称性,取永磁电机的周向1/N模型进行计算,其中N为定子槽数和转子极数、槽数(分析对象为异步启动永磁同步电机时存在)的最大公约数;②忽略绕组趋肤效应和临近效应的影响,认为电机绕组内不同位置的发热情况一致;③绕组端部伸出部分用等长的直导体、绝缘等效;④常规永磁电机通过热辐射散出的热量极小,一般可忽略,计算时仅考虑固体部件的热传导和固体-流体交界面的对流传热。
根据基本假设,由于电机的对称性,需在1/N模型周向断面设置绝热边界;在机壳外边面和腔内散热面设置对流传热边界。其中:绝热边界表示由该面散热的热功率为零,无须调整基于有限公式法的温度场数学模型;对流传热边界反映沿散热面散出的热功率与散热面面积、散热面温度及周围流体介质温度的关系,可通过强加散热项实现:

式中:MR为对流传热本构矩阵;Tfluid为冷却介质温升,K。
3.2 计算平台搭建
在式(1)和(2)基于有限公式法的永磁电机温度场数学模型中,拓扑矩阵G反映原空间单元的线(节点联结)特征。为了实现全求解域的一致性,编程时在构建离散控制方程前设置单元线的正方向,如图3所示。
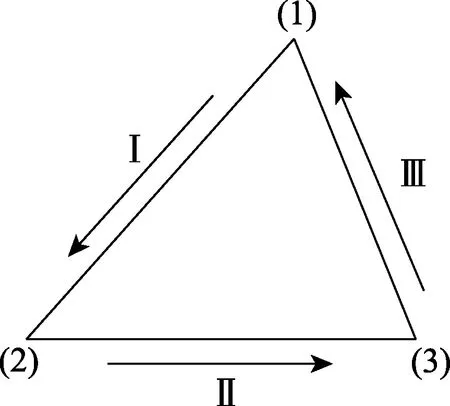
图3 单元正方向
由第2 节中的分析过程可知,研究对象为沿单元线传递的热功率,故取射出节点对应单元线方向为正、射入节点对应单元线方向为负,得到图3 对应单个单元的拓扑矩阵G为:
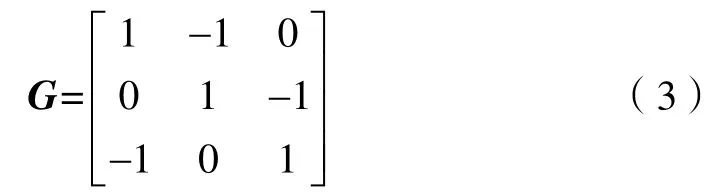
本构矩阵M为对角矩阵,其元素反映映射空间单元面面积、材料导热系数、原空间单元线长度:
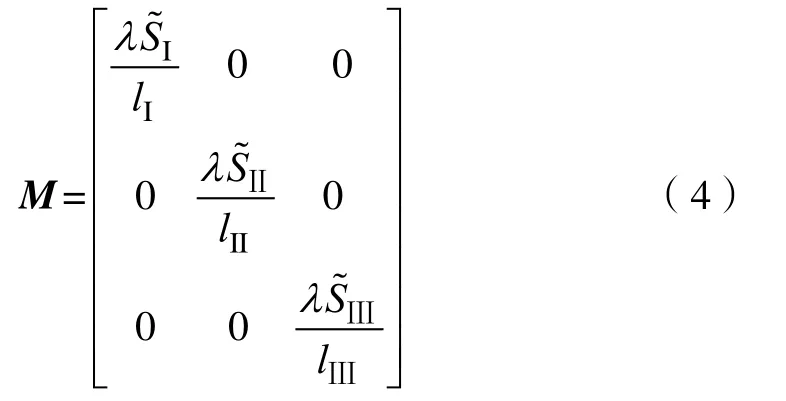
式中:λ为导热系数,W/(m·K);为映射空间单元面Ⅰ的面积,m2;lI为原空间单元线Ⅰ的长度,m。
对流传热本构矩阵MR亦为对角矩阵,其元素反映对流传热系数、映射空间单元面面积。当图3 所示单元在对流传热边界上时,有:

式中:α为对流传热系数,W/(m2·K)。
4 基于计算平台的永磁电机温度场仿真
应用基于有限公式法的永磁电机温度场计算平台,仿真分析一台100 kW 机壳外自扇风冷永磁同步电机的温度场分布。电机基本参数如表1 所示,冷却结构如图4 所示。
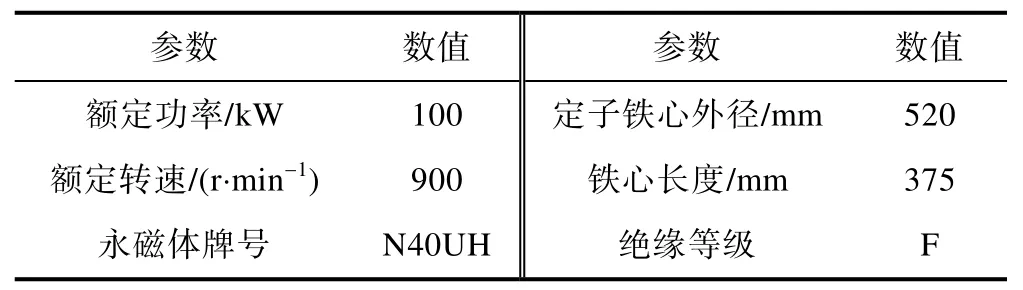
表1 100 kW 永磁同步电机基本参数
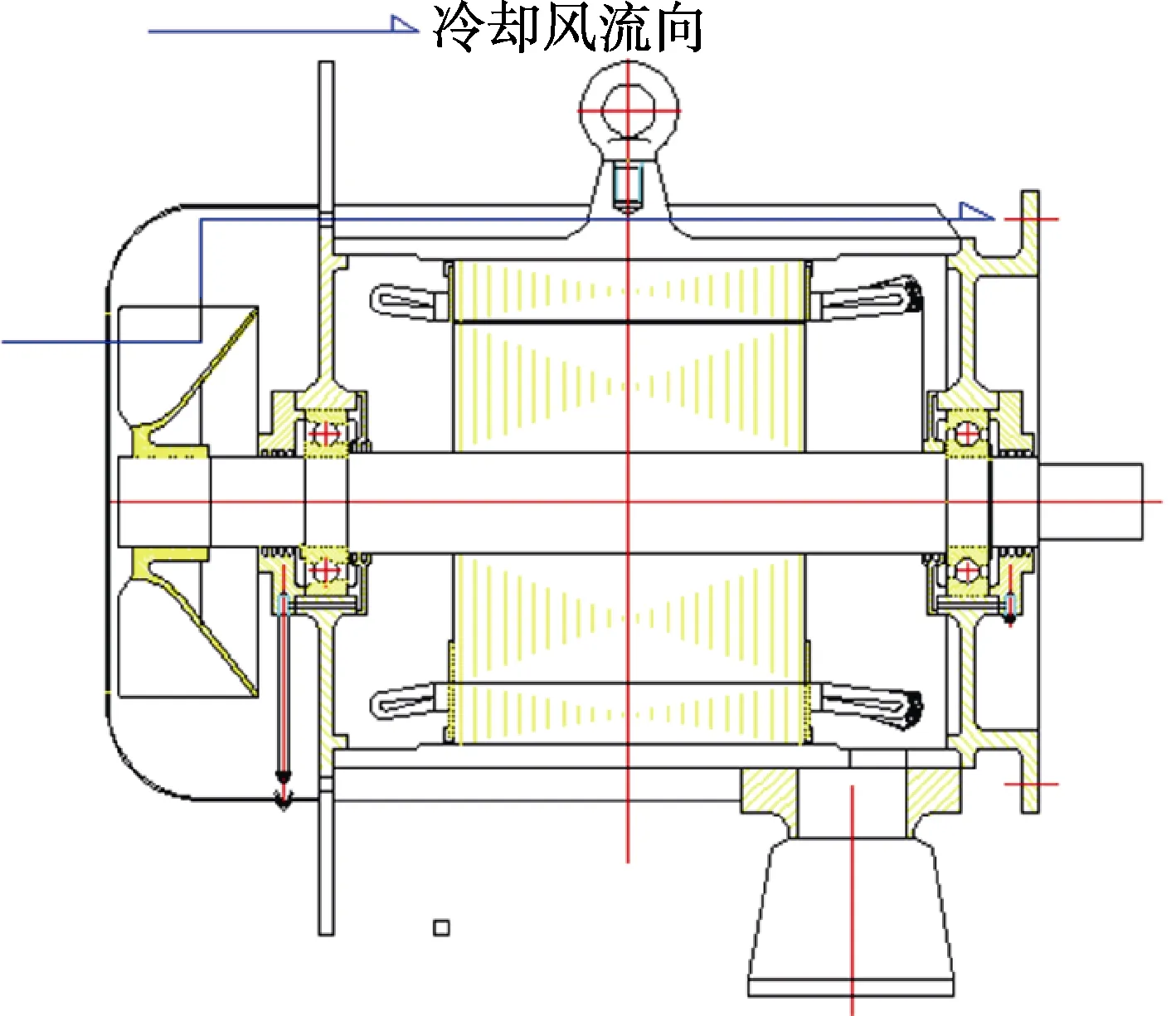
图4 电机冷却结构
计算得到电机整机温升分布如图5 所示。图5 中电机最高温升为70.4 K,位置出现在电机绕组端部。图6 为绕组温升分布。可以看出,由于冷却风在机壳外沿轴向吹拂,电机非驱动端绕组温升较低、驱动端绕组温升较高。由于电机腔外冷却风的吹拂冷却作用,电机绕组温升较低,根据F 级绝缘的温升限制可知[13],该冷却结构满足电机散热需要。
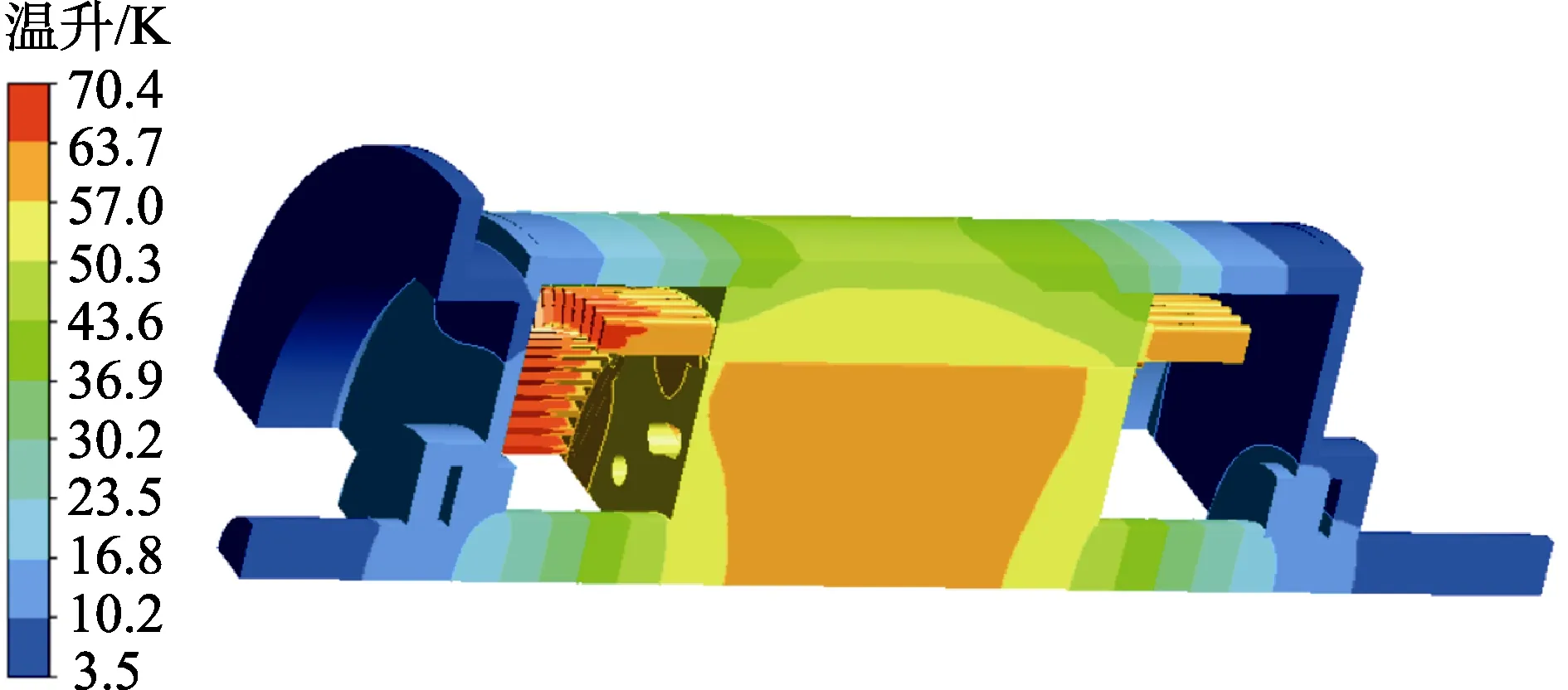
图5 电机整机温升分布

图6 绕组温升分布
5 结语
温升的准确分析和精确计算是永磁电机设计类课程中的重点环节之一,直接影响所设计永磁电机的运行可靠性和输出转矩能力。由于常规数值计算技术的离散过程数学变换复杂,学生难以清晰掌握其核心机理和关键方法。
(1)本文从物理意义清晰明确的有限公式法出发,通过基于有限公式法的复型单元物理量变换,推导其温度场数学模型,从而提高学生对永磁电机温度场数值计算方法的认识和理论分析能力。
(2)立足于永磁电机有限公式温度场数学模型,分析温度场中的基本假设和各类边界条件,搭建基于有限公式法的永磁电机温度场计算平台,使学生掌握永磁电机发热与散热分析及其数值编程方法。
(3)针对一台100 kW 永磁同步电机,计算其温升分布状态,验证其冷却结构的有效性,从而培养学生由基本理论和方法出发解决复杂工程案例的能力。
