基于时段偏好的高速铁路列车停站方案双层规划方法

2021-04-06樊昊煜司晓鑫黄志鹏

铁道运输与经济 2021年3期

蔡芸，王涛，樊昊煜，司晓鑫，黄志鹏

（1.中国铁路兰州局集团有限公司财务部，甘肃兰州 730000；2.中国铁路兰州局集团有限公司华澳铁路综合工程公司，甘肃兰州 730000；3.兰州交通大学交通运输学院，甘肃兰州 730070；4.中国铁路兰州局集团有限公司兰州车务段，甘肃兰州 730050)

0 引言

高速铁路的发展使得旅客出行不再局限于到达目的地，对于出行时段也有了更多的关注，旅客会根据原有的经验习惯与出行目的来选择最理想的出行时段。在高速铁路一日运营时段内，旅客出行需求表现出明显不均衡的时段偏好。此外，铁路部门在组织运营时也应当制定不同时段的列车停站方案。

在以往研究中，牛丰等[1]根据旅客出行目的不同确定了旅客需求置信度，以停站总时间最小为目标建立了高速铁路列车停站方案优化模型；Shang等[2]在时空状态三维网络中说明不同车站接收到的列车座位容量和旅客候车人数的信息不同，因此基于容量限制下优化列车停站方案，合理安排所有旅客乘车；Qi 等[3]结合客流分布特点对列车运营区段和停站方案进行了综合优化；Niu 等[4]考虑时变需求以及最大限度减少旅客等待时间，优化停站方案；许若曦等[5]基于减少列车中小站停站次数，增加相邻大站间站站停列车等策略来优化列车停站方案；黄志鹏[6]证明了基于旅行时间的旅客满意度与不同停站方案的列车开行次序密切相关；高明瑶等[7]建立多目标混合0-1 规划模型，运用理想点法和遗传算法求得列车停站方案优化解；Yue 等[8]使用拉格朗日松弛法将数学模型转换为简单的线性规划问题，然后基于列生成算法通过迭代过程更新受限主问题(RMP)和子问题来寻找最佳解决方案；张小炳等[9]结合优化停站方案的模型特点，设计了具有自适应性的遗传退火算法，控制全局的寻优方向，模拟退火的邻域搜索策略提高算法的邻域搜索能力，最终快速搜索高质量的解；Dong 等[10]用扩展的自适应大邻域搜索元启发式方法对通勤铁路列车停站计划和时间表整合优化。

为此，基于旅客对出行时段的偏好建立一个双层规划模型来优化各个时段某一高速铁路不同停站方案列车的开行数量，并将客流分配在各个出行时段上，使旅客出行需求与列车停站方案相互影响。研究在既有文献基础上做了以下创新。首先，同时考虑旅客的出行时段偏好与列车停站方案，并将多OD 客流需求分配在各个出行时段上；其次是不同于以往周期化的停站方案优化[11]，研究制定了按照出行时段分别优化的停站方案。

1 基于时段偏好的高速铁路列车停站方案双层规划模型构建与算法

1.1 问题描述

（1）旅客出行时段选择博弈。高速铁路全天的发车时间通常在6 : 00—22 : 00，以1 h 为一个时段，将6 : 00—6 : 59 标记为时段1，按照时间顺序依次编号2，3，…，16，共16 个时段。不同时段对旅客的吸引度不同，同时，不同时段的可达度也不同。旅客对各个出行时段的偏好性，一方面表现为不同时段对旅客的吸引度具有很大差异，这种差异是客观存在的，受到多种客观因素的影响，如通勤客流占全部客流比重较大的车站，对旅客吸引度最高的时段为早晚高峰时段；又如旅客总是期望在城市公交方便的白天时段出行等，都是影响旅客选择出行时段的客观因素。对所有车站以往的客流数据统计分析，按照平均时段客流比例得出每个车站的时段吸引度。另一方面，旅客对各个出行时段的偏好性，还表现为旅客对不同时段可达度的选择。当某个出行时段的吸引度较大时，大量的旅客均期望在这个时段出行，这时这个时段的可达度会大大降低。或者旅客为了确保能够在这个时段出行，其必须提前很早购票，使得旅客的出行灵活性降低。因此，旅客会根据出行经验，在时段吸引度和可达度之间进行博弈。博弈的结果是部分旅客偏好于吸引度，降低了可达度；部分旅客偏好于可达度，选择吸引度较低的时段出行。最终形成一个UE 平衡状态，即旅客选择出行的任意时段，其出行阻抗都是一样的。

（2）列车停站方案选择博弈。铁路运营部门在制定列车停站方案时，要考虑2 个方面的因素，一是了解旅客对出行时段的偏好，二是降低运营成本。研究以出行时段为单元，依据旅客对时段的偏好性，分别制定各个出行时段的列车停站方案及同种停站方案的列车开行数量，最大限度地满足差异化的时段出行需求。同时列车开行数量和停站次数越多，其成本也越大。因此，在满足旅客出行需求时，也要考虑运营成本问题。将符合停站约束的所有停站方案作为备选方案，各个时段列车停站方案均是备选方案中的一种或多种。

（3）优化思路。在输入端确定始发站至终到站间单方向的OD 客流需求、列车停站方案备选集和各车站的不同时段的旅客吸引度；输出端为各时段平衡配流结果、各时段列车停站方案。在双层规划模型中，下层的配流结果会影响上层的列车停站方案及列车开行数量；上层模型确定的停站方案会影响旅客的出行时段选择，进而影响各时段的配流结果。优化流程如图1 所示。

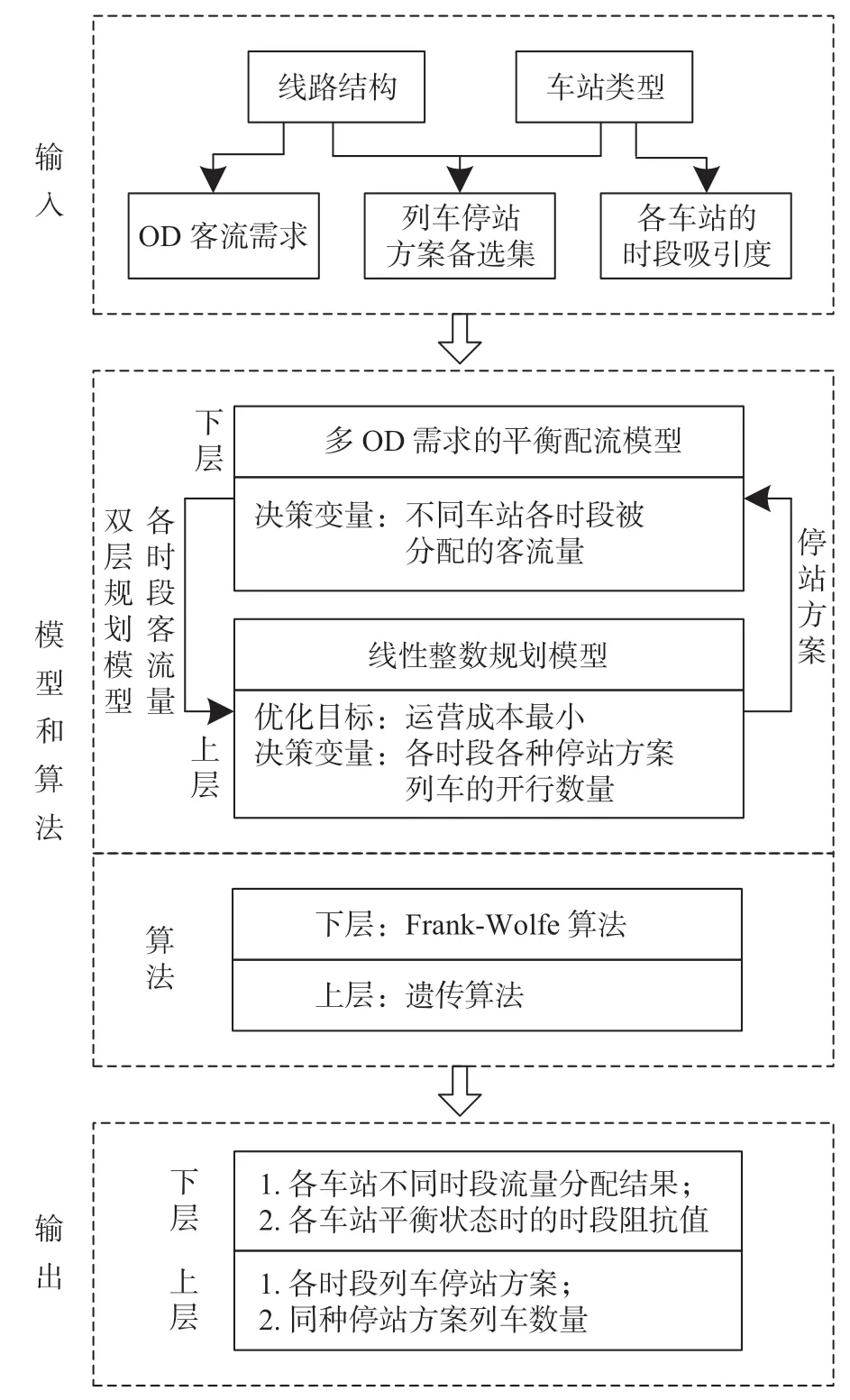
图1 优化流程Fig.1 Optimized flow scheme

1.2 模型构建

（1）符号约定。①集合和下标。S为车站集合；H为列车停站方案集合；T为出行时段集合；i，j用来标识车站，i，j∈S；h用来标识列车停站方案，h∈H；t用来标识出行时段，t∈T。②输入参数。qij为车站i→j的客流需求量，人；为车站i在第t时段无流量加载时的时段阻抗；为在第t时段能够分配给车站i的最大客票数，张；Rh为第h种停站方案列车的开行成本，元；Ft为第t时段，始发站的发车能力，列；为第h种停站方案的列车分配给车站i的票额比例；α为调节系数；Y为列车定员数，人。③决策和辅助变量。为车站i→j的客流被分配到第t个时段的客流量，人；为0-1 变量，代表第t时段第h种停站方案列车是否开行；为下层决策中在车站i上车的客流被分配在第t时段的客流量，人；为上层决策中第t时段第h种停站方案列车的开行数量，列。

（2）上层规划。优化目标为铁路运营成本最小化，目标函数如公式(1)所示。

约束条件包括发车能力约束和各时段供需平衡约束，其中发车能力约束为

各时段供需平衡约束为

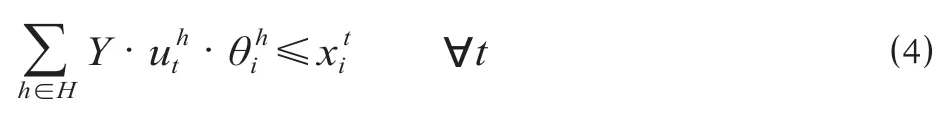
式中：Y·表示第h类停站方案列车的全部席位数量，个；Y··表示第h类列车提供给车站i的客票数，张。

（3）下层规划。①阻抗函数及客流均衡条件。旅客对各个出行时段的偏好性受到时段吸引度和时段可达度的影响。时段吸引度是客观存在，可达度与时段上加载的流量有关。据此构造各车站不同出行时段的阻抗函数，如公式(5)所示。

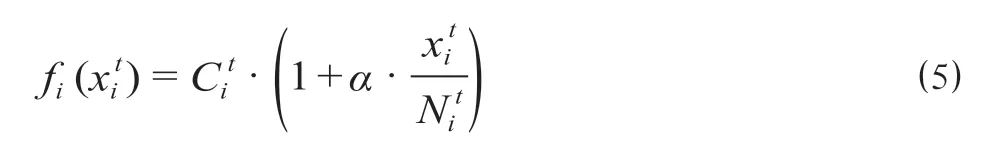
其中的取值与时段吸引度负相关，时段吸引度越高，取值越小。

对于在车站i上车的旅客，当时段t有流量加载时，即＞ 0，出行阻抗为最小；当时段t无流量加载时，即= 0，出行阻抗大于均衡状态时的阻抗。由于不同车站的客流状况不同，因此用户均衡(User Equilibrium，UE)条件也不同，如公式(6)所示，fimin表示车站i的旅客最小出行阻抗。

其中，公式(8)满足了客流守恒，即客流需求被分配到了阻抗最小的各个时段；公式(9)表示车站i→j的客流被分配在第t时段流量为正值；公式(10)表示任意时段t的流量由多个OD 客流构成。

1.3 算法设计

双层规划问题被公认为是极其困难求解的优化问题之一，采用遗传算法对上层规划求解，同时运用Frank-Wolfe 算法求解下层规划。

（1）染色体编码。采用0-1 编码和整数编码2种编码方法[12]求解模型。其中0-1 编码确定各时段各种停站方案的列车是否开行，即“1”表示开，“0”表示不开；整数编码确定各时段各种停站方案的列车的开行数量。2 种编码的染色体均由16 个基因片段组成，分别表示各个时段t上不同停站方案和开行数量。染色体示意图如图2 所示。

图2 染色体示意图Fig.2 Chromosome schematics

（2）算法流程。采用基于嵌套Frank-Wolfe 算法的遗传算法对模型进行求解。其中，上层决策变量用遗传算子编码，下层规划用Frank-Wolfe 算法求解。算法的具体实现步骤如下。

步骤 1：初始化。按照上述染色体编码规则和约束条件(8)，随机生成规模为popsize的初始停站方案()的可行解种群；设置上层规划最优目标E*= 0；设置最优停站方案集W*为零向量；迭代次数b= 0。

步骤 2：检查和判断。依次检查各染色体在时段t上第h类停站方案是否在车站i和j均停车，如果满足，将时段t纳入i→j的客流出行时段，停止检查；如果不满足，继续检查，直到时段t上所有停站方案均检查完毕。完成i→j客流可选择出行时段的集合，转下一步。

步骤 3：用户平衡配流。对于当前开行方案W(i)，用Frank-Wolfe 算法求解下层规划，得到符合Wardrop User Equilibrium 准则的，并记录所有可行解对应的平衡配流结果和阻抗值。

步骤4：整数编码。对步骤1 产生的0-1 编码染色体中“1”的基因位置随机赋1 个整数值，并满足公式(8)、公式(10)约束。

步骤 5：遗传操作。对列车开行数量()的初始种群进行选择、交叉和变异操作，搜寻当前种群中适应度最高的可行解W(b)，并更新最优停站方案集W*=W(b)；迭代次数b=b+ 1。

步骤6：终止检验。如果迭代次数b大于迭代上限Ge，输出最优解W*，否则，转步骤5。

图3 西兰高速铁路车站示意图Fig.3 Stations on Xi’an-Lanzhou high speed railway

2 案例分析

2.1 参数设置

（1）线路和车站。以西兰高速铁路(西安北—兰州西)为例。为了计算方便，将兰州西站编号为1，按照上行方向依次编号，西兰高速铁路车站示意图如图3 所示。

（2）OD 客流需求。为了全面了解旅客出行从出发到终到的过程，旅客起讫点的OD 客流需求是研究列车开行方案的基础，它反映了最直接的客流需求。西兰高速铁路OD 客流需求如表1 所示。

（3）列车停站方案备选集。西兰高速铁路共设车站10 座，其中兰州西、西安北为始发、终到车站，必停车。另外在4 个区域中心所在的定西北站、天水南站、宝鸡南站、咸阳秦都站必停车。在其他车站设置停车次数上限为2 次，则全部停站方案为列车停站方案如图4 所示。

其中，每种停站方案的开行成本为R= {8.0，8.2，8.3，8.3，8.3，8.7，8.5，8.5，8.6，8.6，8.7}{。

（4）阻抗设置。各车站在不同时段无客流加载条件下的时段阻抗如表2 所示。其中，距离始发站较远的车站，每日首列车到达该站时的时段会相应延迟，如车站3 到9，用M表示该时段出行阻抗非常大，不可能有流量加载。

（5）其他参数设置。采用16 辆编组CRH2 动车组列车，列车定员Y= 1 220，调节系数α= 3。种群规模popsize= 200，交叉概率Pc= 0.95，变异概率Pm= 0.05，最大停滞迭代次数为10，最大迭代次数为50，平衡配流精度e= 0.000 1。

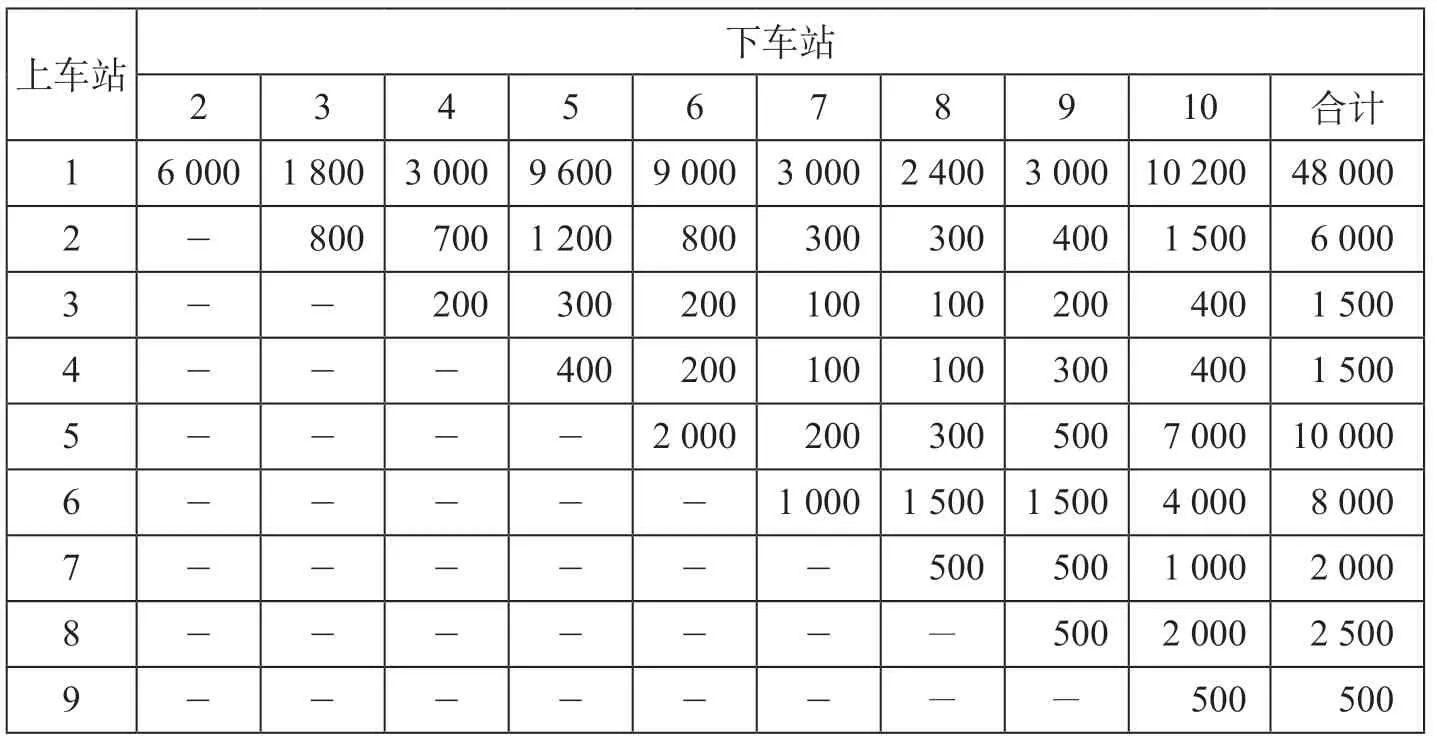
表1 西兰高速铁路OD 客流需求人Tab.1 OD passenger flow demand of Xi’an-Lanzhou high-speed railway

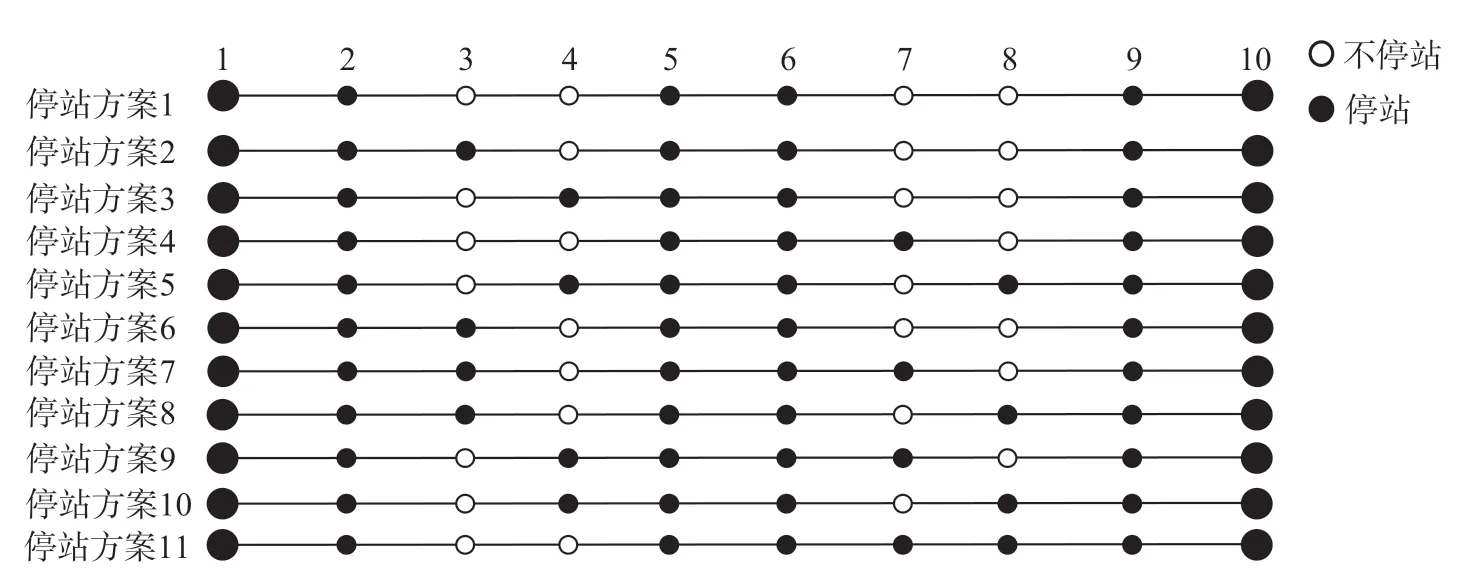
图4 列车停站方案Fig.4 Train stopping scheme

表2 各车站在不同时段无客流加载条件下的时段阻抗Tab.2 Impedance without passenger flow loading in each period

2.2 计算结果分析

（1）下层配流结果。通过软件编程，对该算例进行求解。下层规划计算数据各时段配流结果如表3 所示。各上车站的OD 客流被分配在各个时段上出行，各时段客流具有明显的波动性。

（2）上层开行方案优化结果。通过下层规划的配流结果和上层规划开行方案的迭代，最终经过50 代的进化筛选，得到16 个时段11 种列车的分布情况，第1—8 时段各种停站方案列车开行数量如图5 所示，第9—16 时段各种停站方案列车开行数量如图6 所示。各类列车均有开行，能够服务沿途所有车站的旅客乘降。但是各类列车的分布不均匀，这与不同OD 客流量大小有关。最终优化的列车停站方案，第1—8 时段列车停站方案如图7 所示，第9—16 时段列车停站方案如图8 所示。

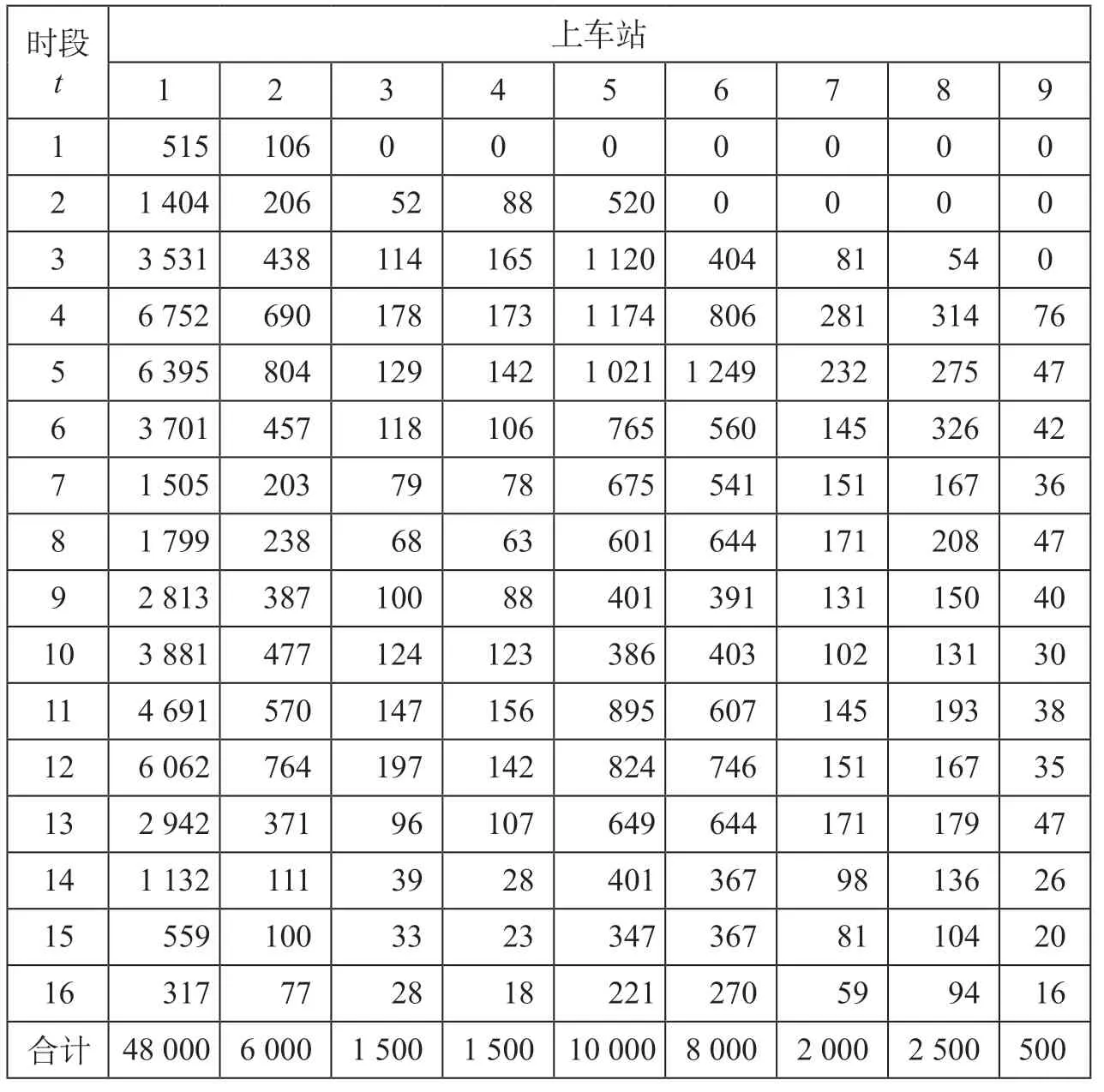
表3 各时段配流结果人Tab.3 Distribution result of each period

图5 第1—8 时段各种停站方案列车开行数量Fig.5 The number of trains in various train stopping scheme during periods 1—8

在传统的列车开行方案设计中，区段内开行列车数是由最大断面客流需求计算得到的，这在一定程度上体现了卖方市场的特点，使得旅客出行选择的方案相对较少，客流量分配的优化目标是基于Wardrop 第二原理(系统最优)的。而由于本次研究模型的流量分配模型是按照交通网络配流Wardrop 第一原理——用户均衡(UE)进行的，其目标是要达到相同OD 的旅客选择各个出行方案(不同时段的不同类型列车出行)的总阻抗(广义费用)相等且最小。当阻抗函数中列车能力参数过小时，在不允许列车超员的情形下，是不存在“相同OD 客流最小且相等的流量分配方案”的。研究的基础是为了提供以人为本的优质服务，以用户为中心，并综合考虑企业运输成本而设计的列车开行方案。