格林公式及其在微分方程中的应用

魏其萍，王 跃 *，蔡梅梅，何小斌

（1. 贵州民族大学 数据科学与信息工程学院, 贵州 贵阳550025；2. 贵州大学 数学与统计学院，贵州 贵阳550025；3. 遵义师范学院 数学与统计学院，贵州 遵义563002）

格林公式在数学、工程、物理等相关专业中为人们所熟知，然而一维情形，格林公式又叫做分部积分法，在涉及到定积分的计算或者估值的问题中，格林公式扮演着不可或缺的角色，给各种复杂计算带来了便利。

1 格林公式

格林公式在涉及到定积分的问题中比较常见，而定积分通常表示的是某些函数围成区域的测度，一维函数定积分表示面积，二维函数定积分表示体积，高维函数定积分也常被称为超体体积，格林公式在定积分问题上的主要作用之一是将函数在区域内部的积分与区域边界上的积分相互转化，因此在很多涉及到定积分的问题中，格林公式的巧妙应用凸显出相当强的优势。

1.1 分部积分法

格林公式主要用于计算定积分，一维情形定积分表示自变量坐标轴、区间两个端点的分割线和恒为非负的因变量曲线四条曲线围成的区域面积，但是在实际坐标中不难发现，因变量曲线可能在自变量坐标轴的两边都有，也就是说不可能恒为非负，因此定义了负部的定积分也为负。由于在定积分的计算中利用不定积分的相关性质可以简化计算，从而有必要先了解不定积分的分部积分法，然后再介绍定积分的分部积分法。

对于定义区间Ω 上的函数f（x）和g（x），分部积分法可表述为：

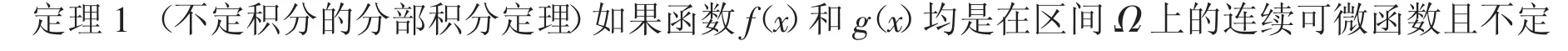
注意在后一式中，务必记住f 和g 都是关于自变量x 的函数f=f（x），g=g（x）。显然，定积分的分部积分公式与不定积分的分部积分公式看起来非常相似，但定积分的每一项都带有积分限，不定积分只是表示函数族，从而没有带积分限。

注1 定积分的计算中，充分利用不定积分的原函数，可以有效解决很多问题。 但一维函数定积分表述的是面积，是一个数值，当定积分为无穷大时称定积分不存在；而不定积分表述的是积分函数的一族原函数。 从形式上看，积分函数具有原函数时，该积分函数的定积分不一定存在，而积分函数的定积分存在时，该积分函数的原函数可能不可以表示成初等函数。如在［0，+∞）上f（x）≡1 的原函数为F（x）=x+C（C 为任意常数），但［0，+∞）上f（x）≡1 的定积分不存在。

注2 从定义上看，对区间Ω，如果存在函数F（x）∈C1（Ω），使得F '（x）=f（x），则称F（x）为f（x）的一个原函数，即F（x）+C（C 为任意常数）为f（x）的不定积分；如果f（x）及区间Ω 端点分割线与自变量坐标轴围成的面积有限，则称该面积为f（x）的定积分。因此，从本质上看，不定积分与定积分没有太大的关系，原函数的存在性搭建了不定积分到定积分的桥梁。

1.2 二维格林公式

在二维函数中，定义区域通常是平面上的点组成的。为此，需要引进单连通区域的概念，即：对于平面区域Ω 来说，如果全落在这个区域内中的任意一条封闭曲线都可以不经过Ω 以外的点而连续地收缩为一点，则称此区域Ω 为单连通的，不是单连通的区域称为复连通的［2］。

单连通区域Ω 上的二重积分和沿其边界的曲线积分之间有如下的关系:

例2 证明式（5）为任意平面图形的面积表达式。

解 设f（x，y）=x，g（x，y）=-y，于是fx=1，gy=-1。根据定积分的定义和格林公式可知式（5）为任意平面图形的面积表达式。

注3 某些定积分计算中，可能要利用坐标变换，再利用格林公式计算结果。甚至在很多情形还可能将低维过渡到高维再降低到低维计算。

1.3 一般格林公式

前两节中主要叙述格林公式在低维空间的情形，下面，将给出一般的格林公式，它不仅在高维空间成立，同样也适用于低维空间。

引理2（高斯-格林定理）［3］设Ω⊂RN是有界区域，∂Ω∈C1，那么对Ω 上的任意函数f=f（x）∈C1（Ω，R）及向量u（x）=［u1（x），…，uN（x）］∈C1（Ω，RN），有

2 格林公式在微分方程中的应用

微分方程的发展立足于实际问题，而通常所遇到的函数不仅仅局限于连续可微函数，因此微分积分问题的发展转入分段连续可微及不可微却可积等各方面。勒贝格积分已占据现代积分问题的主流，它要求积分函数几乎处处连续即可，而不连续的那些地方满足测度为零。而在对应的定积分方面，也不再要求必须满足高阶可微，只要几乎处处可微而不可微的点测度为零即可。同时，从数学分析到泛函分析，解析几何到微分几何再到微分控制微分流形，微分方程的研究方法也在推陈出新，更多信息参见文献［3-14］及其引用文献。勒贝格积分［13］和希尔伯特空间［14］的建立大大扩宽微分方程的研究范围，同时使微分方程与实际问题的联系更加紧密，在天体力学、工程制造、台风预测、优化控制、航天航空等方面微分方程起着不可替代的作用，作为基础学科的数学，推动了现代科技的发展。特别地，格林公式在微分方程弱解的定义中扮演着十分重要的作用，也是一个值得关注的问题。

2.1 推广一维分部积分公式

由于一维定积分描述二维平面上一维函数图形与坐标轴及边界分割线所围成的测度，因此对任意满足－∞≤a

其中端点不能取到时取的是极限值。形式公式中三个部分如果其中两个的值有界，则第3 个必然有界，这样就可以将闭区间推广到开区间甚至整个实数轴上。

2.2 推广广义分部积分公式和格林公式

基于勒贝格测度理论，只要不满足条件的地方测度为零，那么前面的公式都可以完全搬到勒贝格积分问题上。如果用几乎处处表示那些不成立的地方测度为零，于是对可测函数来说有下面的推广格林公式。

推论2 和推论3 的结论是显然的，当不可微的地方测度为零时已经满足定理3 和定理4，这些地方极限存在时也是有限个单点值，其勒贝格积分显然也为零，从而联合积分区域的可加性便得到结论。

2.3 定义边值问题的弱解

在下面的定义和结论中，总给定正整数k 并且假设Ω 是R 中的开区间∂Ω 表示端点，而Ω 是RN（N≥1）中的有界开集且∂Ω 表示边界时类似可以定义并获得相关的结果，另外对于偏微分方程相关问题这里将不再讨论。

则称f=f（x）为第三边值问题的H1类弱解，简称弱解。

3 总结与进一步讨论

本文分为三部分，第一部分总述格林公式，从基本不定积分和定积分的分部积分法入手，再到二维格林公式，最后阐述通用格林公式，内容由低维到高维再到通用形式，循序渐进并给出适当的例子来奠定研究的基础。第二部分概述格林公式在微分方程中的一些应用，首先推广一维分部积分公式到任意区间，其次推广了广义分部积分公式和格林公式，最后介绍微分方程三种边界值问题及其H1类的弱解。显然，弱解问题中，处处与格林公式挂钩。在格林公式基础上，还可以讨论微分问题弱解的可导性。 提到弱解，我们自然想到弱解要比解的性质弱一些，也就是说解包含了弱解的所有性质。

推论4［15］边值问题的弱解不一定具有一阶连续导数。

注4 文献［3，12］已利用算子谱理论给出特征值问题无穷多弱解的存在性，而对于推论4，文献［15］正是从特征值问题出发利用实际例子说明该结论。