基于Lingo 软件的高校排课问题研究
2021-04-06李彬,李枫
李 彬,李 枫
(湖南工学院 数理学院,湖南 衡阳421002)
近年来,高校规模越来越大,课程设置数量越来越多,各高校对排课的个性化需求也越来越多,同时教室以及教师等教学资源又相对有限,排课问题变得越来越复杂。从20 世纪50 年代开始,国内外研究人员开始关注这一问题,直到现在依然是研究热点[1-2]。排课问题在运筹学中又被称为时间表问题,已经被公认为是NP 难题[2]。近年来很多学者采用了遗传算法、禁忌搜索、模拟退火、蚁群算法等启发式算法来研究排课问题,在取得丰硕成果的同时也存在不少问题,比如收敛速度慢,由于约束条件多导致启发式算法经过多次迭代后产生不可行解等等一系列问题[3-8]。文献[9-10]采用了Lingo 软件来求解排课问题数学模型,总体说来模型规模相对较小,且数学模型通用性与可移植性相对较差。本文通过对排课问题的一些常见约束条件进行适当转化,建立了0-1 整数线性规划排课模型,采用Lingo 软件来求解模型。把求解过程当成一黑箱,具体的工作交给Lingo 软件,以此来弥补启发式算法的缺陷。
1 问题提出
某校某学期需要开设Ni门课程,该校共有Nj教师来承担这些课程,涉及到的教学班级数量为Nk,教学任务如表1 所示。
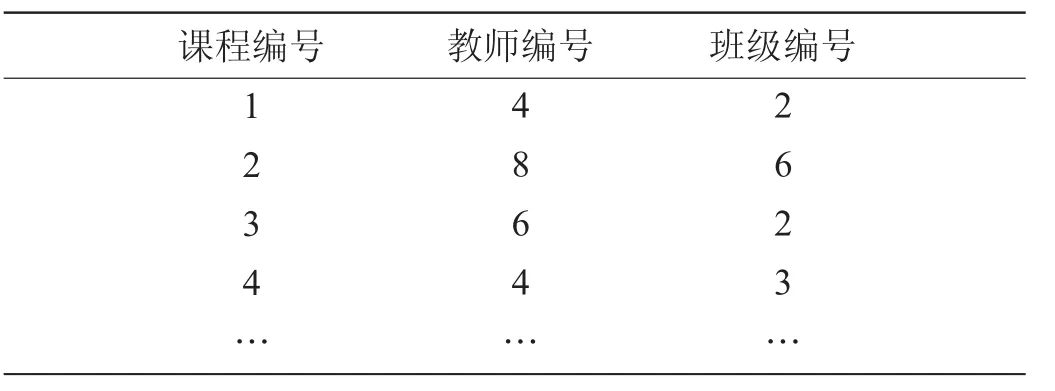
表1 教学任务表
表中第1 列为该校开设的Ni门课程的编号,第2 列为该门课程所对应的授课教师编号,第3 列为该门课程所对应的授课班级编号(暂不考虑合班教学问题,合班教学问题将在模型拓展部分进行分析)。为简单起见,现假定每门课程每周只需要安排一次(每周安排多次的问题将在模型拓展部分进行分析),每周共有Nt个时间段可以安排,该校共有Ns间教室可供安排,问应该如何合理进行排课?
2 排课问题数学模型
2.1 问题分析
合理排课包括很多方面,首先考虑几个最基本的硬性约束。由于同一名教师可能承担了多门课程,同一班级通常开设了多门课程,排课必须保证教师的时间不冲突,学生的时间不冲突,教室不冲突,即每间教室在每个时间段都最多只能安排一门课程。根据这三个约束条件,建立一个最基本的排课模型。
2.2 符号说明
(1)课程编号为i,i=1,2,…,Ni。
(2)教师编号为j,j=1,2,…,Nj。
(3)班级编号为k,k=1,2,…,Nk。
(4)排课时间段为t,t=1,2,…,Nt。
(5)教室编号为s,s=1,2,…,Ns。
(6)教学任务三元集合为U。因教学任务已指明每门课程对应的教师编号、班级编号等信息,可把教学任务表中的每行作为一个元素,得到教学任务三元集合U={(1,4,2),(2,8,6),(3,6,2),(4,4,3),…}。教学任务三元集合中每一个元素都包含了课程编号以及对应的教师与班级编号。构造教学任务三元集合的目的是为了减少排课决策变量数量,减少无效约束条件的数量,为模型求解提供便利。

下文中所涉及的排课决策变量前3 个下标所成3 元组必须包含于教学任务三元集合中,不再重复说明。
2.3 模型建立

3 模型求解实例
3.1 中等规模的问题
取Ni=500,Nj=1 000,Nk=50,Nt=20,Ns=30,利用Matlab 软件对500 门课程随机生成教师编号以及对应的班级编号,排课时间段取为20 个(每周有5 天可排课,每天有4 个时间段可排课),教室取为30间。在CPU 为AMD A8-5600K 的Win7 系统电脑上,利用Lingo11.0 进行求解,共300 000 变量,约4 000 条约束,大约14 min 得到了可行解。高校院系内部的专业课排课问题规模与之相当,Lingo 可以完成求解。
3.2 更大规模的问题
当把课程数量、教师数量、班级数量、教室数量分别扩大2 倍再进行求解时,模型规模已经超过Lingo11.0 的内存限制,求解失败,更大规模问题的求解需要更高性能CPU 以及高版本的Lingo,或者有更好的求解策略。笔者在此提出一种分步排课的策略,例如,可以首先利用Lingo 排定全校各班级的数学、计算机、英语等公共课,等这些课程排好后,相关的排课决策变量就成了常值,模型规模就大大变小了,再用Lingo 依次对各院系专业课进行排课。
取Ni=1 000,Nj=200,Nk=100,Nt=20,Ns=70,利用Matlab 软件对1 000 门课程随机生成教师编号以及对应的班级编号,排课时间段取为20 个,教室取为70 间。分4 次对该问题进行求解,第1 次求解前250 门课程的排课问题;等求解结束后把相应的决策变量的结果作为约束条件加入模型,然后对前500门课程的排课问题进行求解;如此重复操作4 次后,就得到了原问题的解。在4 次求解过程中,分别耗时18 min、38 min、70 min、110 min,总计耗时4 h 左右,用时间换空间的策略完成了问题的求解。
4 模型拓展
4.1 教室的容量限制问题
排课过程中,有些教室由于容量限制或其他问题,不适宜把某些课程安排在某些教室,可以在模型中再加入相关约束条件。例如,教学任务编号(3,6,2)不宜安排在8 号教室,则可以加入约束条件∀t,x3,6,2,t,8=0。
4.2 课程的排课时间特殊要求

4.3 教师排课时间的特殊要求
某些教师由于公务原因,某些时段不能排课。例如,教师6 不宜在第4 时间段排课,则加入约束条件∀i,k,s,xi,6,k,4,s=0。
4.4 课程每周需要安排多次

4.5 合班教学问题
很多高校都有合班教学的现象。假如(2,8,6),(3,6,2)两教学任务中,6 号班级与2 号班级是合班产生的教学班级,且6 号班级与2 号班级中包含有相同的学生,那么两门课程不能安排在同一时间段,
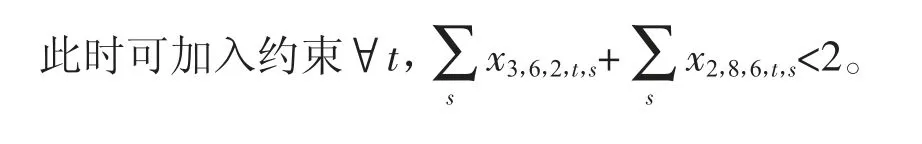
5 小结
针对排课问题中常见的硬约束、软约束问题,建立了0-1 整数线性规划模型,模型通用性较强,且非常适合Lingo 软件编程求解。对中小型规模问题,可以借助Lingo 方便地进行求解,基本能够满足大学院系内部专业课排课需求。对于更大规模问题,主要有两条解决思路:其一可以采用性能更好的电脑、高版本的Lingo 软件来弥补;其二可以把大问题进行分割、分步骤排课。
本文给出的排课模型中无目标函数,具体应用时可根据学校的需求加入相关优化目标函数。比如可把排课的分散程度、教师是否连堂等指标作为优化目标等等。超大规模排课问题以及更多的排课优化指标问题,值得进一步探索。
