基于纬编针织物特性的静电吸附力模型

2021-04-06刘立东李新荣刘汉邦李丹丹

纺织学报 2021年3期

刘立东，李新荣，刘汉邦，李丹丹

(1. 天津工业大学机械工程学院，天津 300387； 2. 天津市现代机电装备技术重点实验室，天津 300387)

纺织服装产业是我国重要的民生产业，在国民经济中发挥着重要作用。随着生活水平的提高，人们对服装的需求不再局限于遮羞蔽体，而是希望通过服装展现自己的风格与气质，由此以用户为中心的设计理念被广泛接受[1]。私人定制将会成为未来纺织服装行业的主要发展方向，而服装私人定制化的发展和壮大，离不开工业机器人技术的支撑，与传统操作相比机器技术能够很好地降低人工成本，改善工人工作环境。在服装生产过程中面料的抓取和转移是绕不过的一环，而机械手在抓取过程中都是通过末端执行器与工件接触，因此机器人末端执行器通常被认为是工业机器人的关键部件，如今制约工业机器人在纺织行业推广的瓶颈主要是末端执行器核心技术，故需要加大对末端执行器抓取力的研究。

传统服装加工中，面料的抓取和转移主要依靠人工来完成。为解决面料抓取和转移的问题，Koustoupardis N[2]开发了一种三指式抓取器，用于抓取面料，虽然能够实现对面料的抓取,但是定位精度较差；Sun B[3]设计了一种基于静电吸附技术的夹持器，可以实现对柔性面料的抓取和转移；Cubric G等[4]应用负压吸附原理制作了负压吸附式真空吸盘，由于面料结构疏松多孔，在吸附时会产生很大的噪声，同时也会有很大的能量损失；瞿锦程[5]使用针刺机构实现对面料的抓取和定位，针刺的使用会对面料的质量产生一定的影响。对比几种抓取转移方式，机械抓取和负压吸附定位精度相对较差，负压吸附的能量利用率不高，吸附时还会产生很大的噪声，针刺结构又会影响面料的质量。相比之下静电吸附具有安全稳定性更高、节能、定位精度高、对面料损伤更小等诸多优势，所以静电吸附更加适合应用于对面料的抓取和转移。2009年，Sogard M R等[6]对基于库伦作用的静电吸盘的静电性能进行了分析评估；Schaler E W[7]将静电吸盘应用于航天飞船的维修，可以实现对人造卫星部件的稳定抓取和移动；Dhelika R等[8]提出使用双极性静电抓手，实现对柔性物体的抓取和转移。虽然静电吸附技术有所发展，但针对纺织服装行业的应用始终未能实现大的突破，静电吸附技术在服装加工中应用面临的首要问题是要从理论角度对静电吸附力大小进行研究。

本文基于织物特性对静电吸附力进行研究，首先分析织物的结构特性，构建织物单元的三维仿真模型，其次分析组成织物的纤维成分对织物相对介电常数的影响，然后以纬编针织物为例，构建纬编针织物吸附力模型，并通过仿真验证模型的正确性。该静电吸附力模型充分考虑到织物的结构参数和介电特性对静电吸附力大小的影响，在已知织物结构参数和介电特性时能够准确计算静电吸附力的大小，对静电吸附技术在服装制造行业的使用具有重要的现实意义，可为纺织服装行业的自动化提供理论参考。

1 静电吸附力建模

当物体处于电场中时，会由于静电极化而受到电场力，根据库伦作用可知，静电吸附力的大小和织物与极板之间的距离及织物的相对介电常数有关。纤维的内部结构、空气湿度等都会对织物的介电常数产生一定的影响，但是随着组成织物的纤维种类的增多，各种纤维的空间占比及分布就成为了影响织物介电常数的主要因素。织物的结构参数会对极板与织物之间的距离产生影响，随着织物结构参数的改变，有效吸附面积的大小会产生变化。本文首先对织物的结构参数进行分析，建立织物的三维模型，然后分析组成织物纱线的成分对织物介电常数的影响，从而建立基于织物特性的静电吸附力模型。

1.1 织物结构单元模型的建立

织物的外观特征及内在性质都是由纤维的排列状态及其相互作用决定的。机织物和针织物分别是通过纱线按照一定的起伏规律和圈套规律形成的纱线集合体，非织造布则是由纤维之间相互纠缠黏结固着生成。机织物的结构最为简单，纱线的空间分布以及纤维的结构对静电吸附力影响细微；非织造布纤维排列紧密，对非织造布的静电吸附力计算可以等效为实体模型；与前二者相比，针织物结构多变，在织物中更具代表性，而纬编织物单元是针织物中最基本的结构单元，所以本文以纬平针组织针织物为例进行研究。

纬编针织物的形状如图1所示。这类织物由重复的图案组成，其中织物的面积和质量都与单圈的配置和尺寸相关，因此，对针织物几何形状的研究基本上是对单个针织物线圈的几何形状的研究。

图1 纬编针织物的结构简图Fig.1 Schematic drawing of weft knitted fabric

国内外对于纬编线圈的建模方法主要基于Pierce模型法、分段函数法和样条曲线法3种模式。在Pierce模型[9]中针编弧和沉降弧都用半圆表示，用直线表示圈柱段，纱线线圈的宽度、高度、圈柱长和整个线圈长度之间存在着比例关系，但是用直线描述模型其效果与实际结果相差较远，同时结构也过于理想化。Choi K F等[10]将织物分成8段，每段都有对应的函数描述纱线的走向，这些模型都是在理想状态下建立的，不能很好地反映纤维的受力情况。

在编织时纱线因为受力发生扭曲，这会导致针编弧和沉降弧发生变形，而纱线的截面不会发生变化[11]，所以本文考虑使用椭圆表示针编弧和沉降弧。同时使用非均匀三次B样条曲线表示圈柱段。为了保证不同线圈之间能够平滑衔接，使用正弦函数来表现线圈的起伏，结构简图见图2。图中：w为圈距，mm；h为圈柱高度，mm；d为纱线直径，mm；β为线圈起伏角，(°)；a0为椭圆的长轴长度,mm；a1为椭圆的短轴长度,mm。

图2 纬编针织物线圈的几何模型Fig.2 Geometric model of a weft knitted fabric coil.(a) Front; (b) Side

通过分析图2(b)可以推导出线圈的z坐标表达式：

(1)

式中，α为椭圆的扁系数，其数值等于椭圆短轴a1和长轴a0的比值，取值范围为(0，1)。

弧段使用椭圆进行描述，因此,引入椭圆的扁系数α。AB弧和EF弧关于Y轴对称，因此，只需表达AB段方程上的x，y坐标关系即可。其中AB段x和y的关系如下：

(2)

CD弧段经过AB弧段坐标变换求得，弧段CD段的坐标关系如下：

(3)

圈柱段包括BC和DE段2段，其关于Y轴对称，因此，只需要求解出BC段的曲线方程就可以求得DE段的表达式。

非均匀有理B样条曲线可以进行局部的调整，具有较好的几何特征和灵活性，能够较好地模拟纱线中心轴走向，因此，本文使用B样条曲线构建织物的圈柱段。

线圈模型结构中交织点分布不均匀，建模需要纱线曲线二次连续，故采用三次非均匀有理B样条曲线建立纬编针织物线圈结构模型。三次非均匀有理B样条曲线又叫NURBS曲线，它是由控制顶点和基函数确定的。已知控制顶点Pi(i=0,1,2，…,n)，则k+1阶NURBS曲线[12]的表达式可表示为

(4)

式中:k为NURBS样条曲线的幂次;Pi为控制顶点，又称德布尔点；Ni,k(u)为k次样条曲线的基函数，基函数是由节点矢量U=[u0,u1,…,un+k+1]按德布尔考克斯递推公式[13-14]定义的k次规范B样条基函数，表示为

(5)

式中，当推导过程中出现0/0的情况下，规定0/0=0。

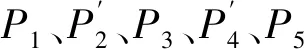
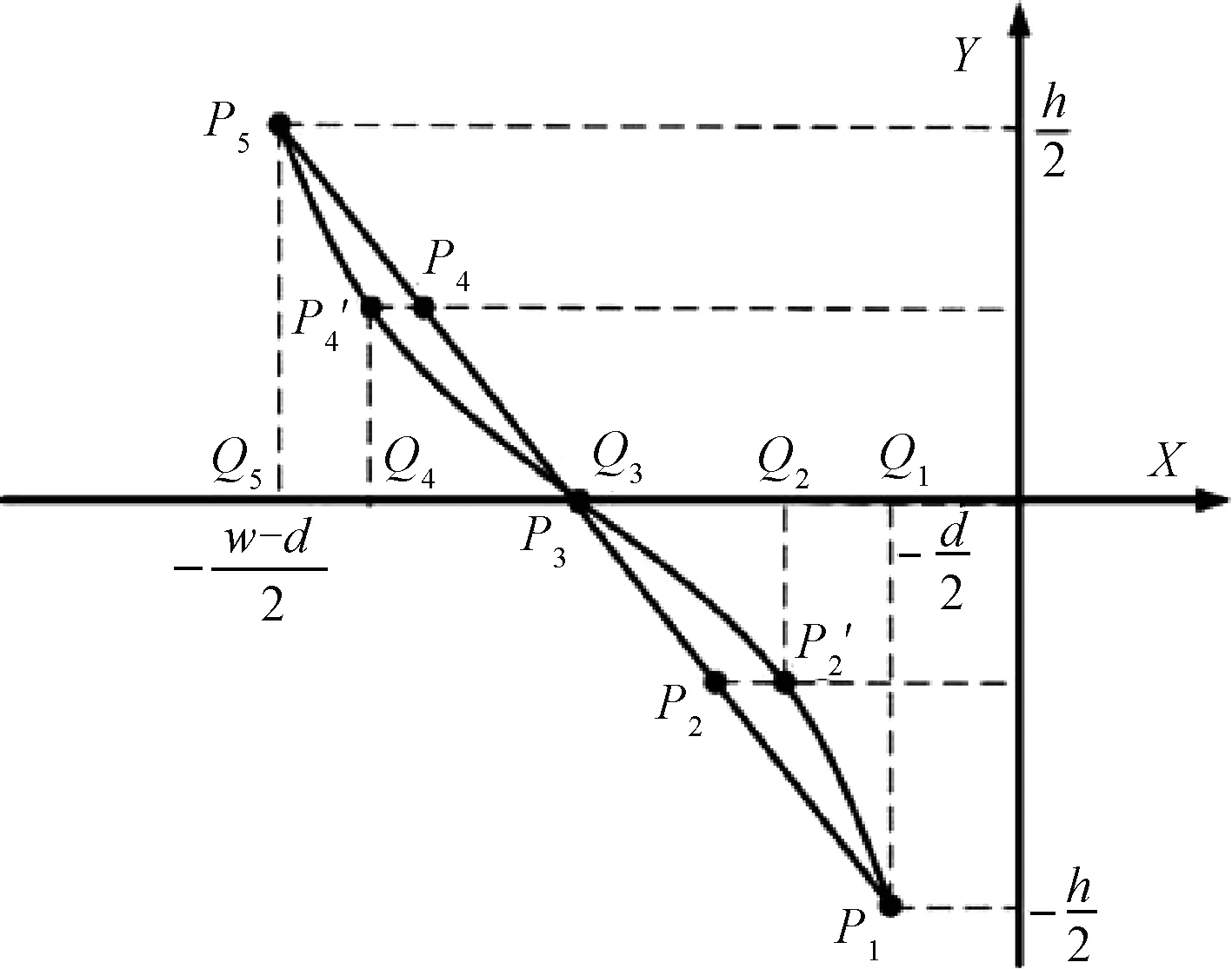
图3 BC段型值点坐标Fig.3 BC segment value point coordinates

则可以求得BC段型值点坐标：

最后根据型值点的分布趋势，反求出控制点列。在NURBS曲线中可以根据节点矢量U的变化求解对应的空间坐标。最后根据曲线上的空间坐标用SolidWorks绘制纬编针织物的三维模型,如图4所示。

图4 纬编针织物的三维模型Fig.4 Three-dimensional model of weft knitted fabric

1.2 织物相对介电常数的计算

根据织物所使用原料的不同可以把织物划分为纯纺织物、混纺织物、混并织物和交织织物。混纺织物凭借其优异的性能在市场中分布较为广泛。纤维是组成混纺织物纱线的最基本单元，在织物中纤维的内部结构及不同纤维的分布形态，将直接影响着织物的相对介电性质。

当纤维暴露在电场中，会引起电通密度D的响应，二者之间存在着以下关系[15]:

{D}={ε0}{εr}{E}

(6)

式中：D为电通密度，C/m2;E为电场强度，V/m;ε0为真空介电常数，数值为8.85×10-12F/m[16]；εr为电介质的相对介电常数,F/m。

对于各向同性电介质材料，方程可进一步表示为

D=ε0εrE

(7)

对于各向异性电介质材料，方程可以表示为

(8)

式中：DX、DY和DZ分别表示各向异性材料在X方向、Y方向和Z方向的电通密度；εrXX、εrYY和εrZZ分别表示在X方向、Y方向和Z方向的相对介电常数，EX、EY和EZ分别表示在X方向、Y方向和Z方向的电场强度。

对于由多种纤维组成的混纺织物，其电磁响应关系符合体积加权平均原理，即混纺织物总电磁响应等价于纤维对混纺织物体积贡献之和。从有限元角度来说，即总电磁响应等于各个单元对整体体积贡献之和，由此可以得出电场强度和电通密度的计算公式：

(9)

(10)

式中:Ei和Di分别为第i个单元上的电场强度和电通密度;Vi为其所对应的体积贡献值。

根据上述公式，混纺织物的等效介电常数[17]可以写为

(11)

分别提取纬编针织物各个单元的体积、单元电场强度和电通密度，根据式(11)即可求得纬编针织物的等效介电常数εr。

混纺织物的等效介电常数计算模型有很多种，为了提高计算精度，同时节省计算资源,本文使用35×35×1大小的随机分布模型，能够真实反映各种纤维在电场中的分布形状。

在随机分布模型中，为了更加准确地反映纤维长度和纤维直径之间的关系，设定纤维的长径比为1 500[18]。建模时，赋予这些结构与混纺织物主要纤维成分相同的电磁参数。计算时建立与体积分数相当的随机数组，按照随机数组选出响应部分的立方体，将之转化为其他纤维的电磁参数。最终得到符合材料的几何模型。图5示出2种不同体积分数纤维的混纺纬编针织物结构。图中f2表示混纺织物中一种纤维的体积分数。

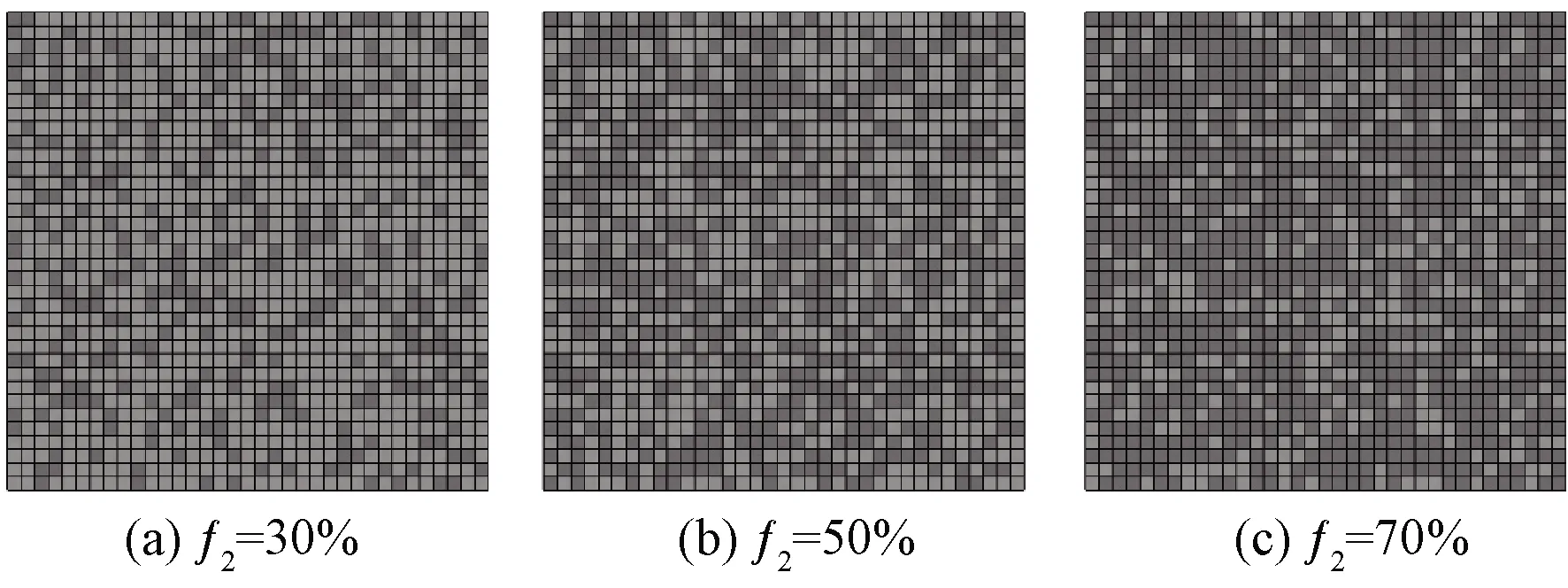
图5 不同体积分数的纬编针织物结构Fig.5 Structure of weft knitted fabric with different volume fraction

设主要纤维成分的相对介电常数为5，次要成分相对介电常数为1。分别通过改变其中一种纤维成分的随机分布和体积分数来分析其对混纺织物相对介电常数大小的影响。表1示出等效介电常数随混纺织物中一种纤维体积分数的变化。

表1 等效介电常数随混纺织物中一种纤维体积分数的变化Tab.1 Equivalent dielectric constant varies with volume fraction of one fiber

纱线纤维的随机分布模型可能会导致某一个单元孤立的情况发生，这与实际纤维分布不符，所以会导致计算结果偏差较大。由表1看出，当体积分数为30%时，最大偏差为0.74%。由此可见，通过这种方法计算相对介电常数的稳定性是非常高的。

1.3 静电吸附力模型的建立

各种纤维按照其分子结构可以划分为无极性分子和极性分子2类。无极性分子在电场的作用下，分子的正负电荷“重心”发生平移感应，生成与电场方向相同的电偶极矩。极性分子在没有外加电场的情况下正负电荷中心不重合，具有一个确定的电偶极矩。由于分子无规则地热运动，在无外加电场时电偶极矩的取向在任何一个方向上都是杂乱无章的，对外不显电性，因为电场的不均匀，电偶极子会受到梯度力的作用。

静电吸附模型如图6所示。图中E0为电极板所产生的电场强度;E1、E2、E3分别表示介质层、空气层和织物所产生的退极化电场。在电极板产生的电场激发下，绝缘介质层和空气层均发生了极化反应，表面产生了束缚电荷。在电场作用下绝缘介质、空气和织物左右表面都会产生与电场方向相反的极化电荷削弱电场。

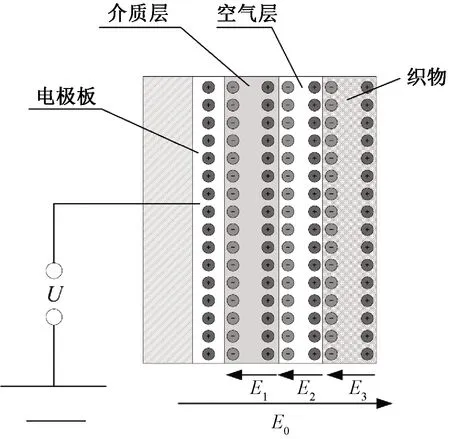
图6 静电吸附模型Fig.6 Electrostatic adsorption model

如图6所示，由于极化现象所产生的极化电场是外加电场与介质极化产生的退极化电场的叠加，则吸附电极所产生的总电场强度为

E=E0-E1-E2-E3

(12)

根据高斯定理可以求得

(13)

(14)

(15)

式中：σ1，σ2和σ3分别为绝缘介质层、空气层和织物的电荷面密度，C/m2；χe1，χe2和χe3分别为绝缘介质层、空气层和织物的电极化率，F/m。电极化率χe和相对介电常数之间存在如下关系：

εr=1+χe

(16)

所以,电场强度可以表示为

(17)

式中，εr1、εr2、εr3分别表示绝缘介质层、空气层和织物的相对介电常数。

电偶极子在电场中的受力可以表示为

(18)

(19)

式中:∑p表示物体内电偶极子的电偶极矩之和,C/m2;ΔV表示电介质中的任一体积元,m3。

电极化强度的计算公式为

P=ε0χeE

(20)

式中,ε0为真空介电常数。

整理式(18)、(20)可得电偶极子在电场中所受的静电吸附力计算公式

(21)

式中:F为静电极板对电偶极子所产生的静电吸附力的大小，N；ΔE02为电场强度沿极板方向的衰减程度，V/m。

从式(21)可以看出，决定静电吸附力大小的主要因素有2个：被吸附物体的相对介电常数和电场强度的变化值。被吸附物体相对介电常数的大小可通过有限元的方法求得，但是电场强度的变化值无法求解。

已知库仑力大小的计算公式为

(22)

式中:q0为产元电荷带电量，C；q1为受力电荷带电量，C；l为2种电荷之间的距离，m；e01为由q0指向q1的节点矢量。根据电场强度的定义，单个电荷所形成的电场强度为

(23)

根据电场叠加原理，电场强度的计算公式可以表示为

(24)

平面电极和被吸附物体之间相互作用的是直接和面料接触的部分,则dq=σds,这里的σ为电荷的面密度,C/m2;q为静电极板上的电荷量;s为静电极板的面积。平行板电容器电荷的面密度可以表示为

(25)

式中：u为电极板两端的电压,V;h′为静电极板与织物的距离,mm。

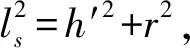
(26)

由此可以得到电场强度的计算公式：

(27)

对r求导可以得出ΔE随距离变化的计算公式：

(28)

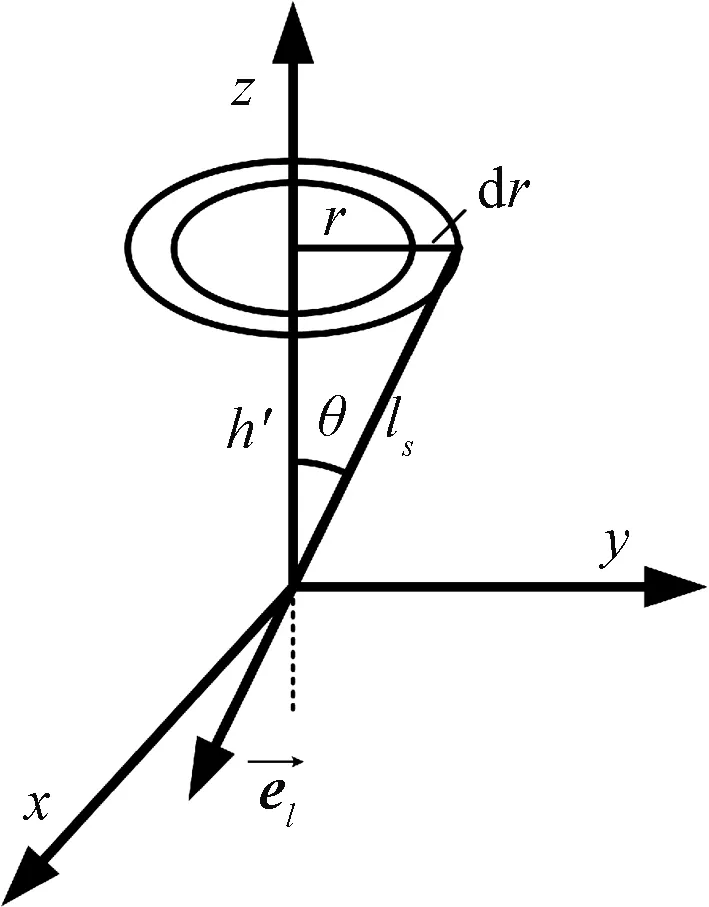
图7 平行板电容器场强分布Fig.7 Field strength distribution of parallel plate capacitor

为分析电场强度变化ΔE与h′之间的关系，设定相对介电常数εr为3 F/m，电压u为2 kV,根据式(28)利用MatLab计算得出电场强度变化ΔE与h′之间的关系，如图8所示。

图8 ΔE大小随h′的变化Fig.8 ΔE magnitude varies with h′

如图8所示，电场强度变化ΔE的大小随着距离h′的增大快速衰减，h′是影响电场强度变化的关键因素。由公式(26)和公式(28)最终得到静电吸附力的计算公式:

(29)

从公式可以得出，吸附力的大小与织物的结构参数、电极板两端电压以及绝缘层的介电特性相关。在不改变其他因素的情况下，可以通过提高静电极板两端电压的方式，提高静电吸附力的大小。

2 仿真验证

为更加准确地计算纬编针织物静电吸附力的大小，同时避免模型的计算量较大,本文将纬编针织物简化为一个织物单元，通过计算电场对一个织物单元的静电吸附力的大小进而求解出电场对整块织物的静电吸附力。简化的织物单元如图9所示。单个织物单元是由1个针编弧、沉降弧和1个完整的线圈组成。

图9 纬编针织物的简化单元Fig.9 Simplified unit of weft knitted fabric

将借助SolidWorks软件生成的纬编针织物结构三维模型导入到三维分析软件COMSOL中,进行仿真分析。纬编针织物的几何参数[19]如表2所示。

表2 几何参数配置表Tab.2 Geometric parameter configuration table

进行材料属性的界定时，将纬编针织物周围的空气域介电常数设定为1。为了确保计算精度，纬编针织物和空气域之间形成联合体。在进行边界条件设定时，设定上极板电压为2 kV，下极板接地构建一个电场环境。

网格的大小和质量直接影响迭代计算速度和最后的收敛情况。纬编针织物模型尺寸小,表面屈曲程度大，所以网格划分时特别需要注意表面链接处的网格矢量。因为多面体具有较多的相邻单元，适用于表面屈曲程度大的几何体，并且梯度计算和流动模拟更为准确，所以本文实验中使用自由四面体网格进行网格划分。网格划分和仿真模型如图10所示。

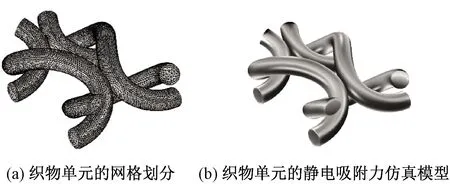
图10 纬编针织物的单元网格划分与静电吸附力仿真模型Fig.10 Mesh division (a)and simulation model (b) of weft knitted fabric units

根据表2中的纱线几何参数，分别应用MatLab和COMSOL进行仿真,绘制出静电吸附力曲线,如图11所示。对比仿真实验和理想的静电吸附力曲线可知，仿真所得的曲线与理想的静电吸附力曲线趋势相同，但在数值上有一定的差异。这是因为数学模型忽略了极板的边缘效应，考虑到极板是无限大的情形，而仿真模型所构建的极板模型大小是有限的，所以理论计算和仿真效果有一定的差异。