Simon 量子算法在对称密码分析中的应用浅析∗

2021-04-06熊家琪黄雅婷

北京电子科技学院学报 2021年1期

熊家琪刘昂黄雅婷

北京电子科技学院，北京市 100070

引言

在量子计算机的出现预期下，量子算法应运而生。量子算法基于量子态的相干性和叠加性可实现并行计算，量子计算机使得量子算法实现强大的并行计算能力成为可能，这种强大的计算能力可以解决以往经典计算机很难解决或不能解决的问题。由此催生了新的密码分析方法，量子算法开始进入现代密码分析领域[1]。

对当前密码学领域影响较大的量子算法主要有Shor，Simon，Grover 算法及其优化和衍生算法。 Shor 算法对公钥密码体制影响深远，而Simon 和Grover 算法则主要影响对称密码体制。

1994 年，Shor 提出了以其本人姓名命名的量子算法--Shor 算法[2]。 Shor 算法可在多项式时间内求解因子分解问题和离散对数问题。它攻破了RSA 和Diffie-Hellman 公钥密码系统，这一发现震撼了公钥密码领域，后量子密码研究也随之产生，NIST 于2016 年开始公开征集后量子公钥算法。近年来，后量子密码成为密码学的热点研究问题。

同年，Simon 也提出一个量子算法--Simon量子算法[3]，主要用于解决特定函数的周期求解问题。与经典算法相比，在查询复杂度上，Simon 算法可以实现指数加速，可将求解函数周期的复杂度由O(nn/2) 次经典查询降低至O(n)次量子查询。它对包括Feistel 结构在内的分组密码构成威胁[1]。

1996 年，Grover 提出了Grover 量子算法[4]。Grover 算法具有加速暴力搜索的特性，从n 个无序数据中搜索1 个特定目标条目，将查询复杂度从经典的O(n) 降到O(n1/2)，实现平方加速。研究发现，使用Grover 算法进行密钥穷举攻击时，其效果相当于将分组密码的密钥长度减少一半。只要将分组密码的密钥长度增加一倍，就可获得同样的安全强度。

这些量子算法的提出对现代密码体制的安全性构成严重威胁，吸引了全世界众多的密码学者加入到后量子密码学的研究中来。本文将重点研究Simon 量子算法在对称密码分析中的应用。

1 Simon 算法简介

1.1 Simon 问题

给定周期函数f:{ 0 ，1}n→ { 0 ，1}n，假设存在唯一的周期s ∈ { 0 ，1}n＼ { 0}n使得f ( x) =f ( x ⊕s) ，x ∈ { 0 ，1}n，求解s。

注意:此处周期不同于常规周期原像的加法运算的关系，而是异或运算的关系。因异或关系满足x，x ⊕s，x ⊕s ⊕s=x，x ⊕s ⊕s ⊕s=x ⊕s，…，故此处一个函数值f(x) 仅对应两个原像x和x ⊕s，值域是定义域的一半。

1.2 Simon 算法

给定一个布尔函数， f: { 0 ，1}n→ { 0 ，1}n，可以求出一个长度为n 比特的异或周期s，使得这个函数在周期s 下保持不变。换句话说，存在一个s ∈ { 0 ，1}n，使得f ( x) = f ( y) x ⊕y ∈{0n，s} 成立。

在经典计算中，求解s 所需的计算复杂度为O(n1/2)，然而，Simon 提出的Simon 量子算法提供指数加速，在量子计算模型下只需要O(n) 次量子查询就可以找到s。 Simon 算法的量子电路如图1 所示。

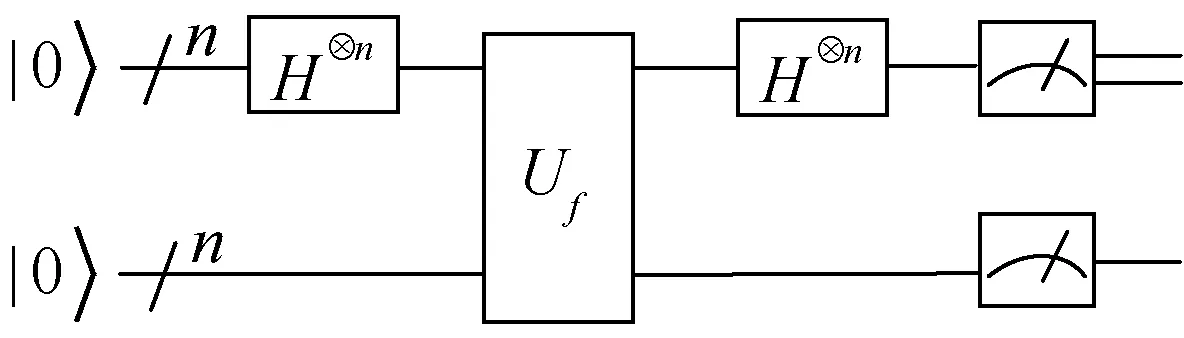
图1 Simon 量子算法

其中⊕表示按位的模2 加。

Simon 量子算法工作步骤如下:

a) 将两个n 位量子寄存器状态初始化为| 0〉⊗n| 0〉⊗n。然后将Hadamard 变换应用于第一个寄存器，用以下方式获得一个相等的叠加:

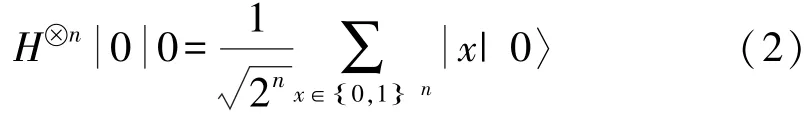
b) 将对函数f 的量子查询映射到:

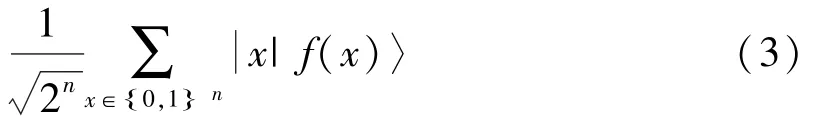
c) 测量第二个寄存器时，观察第一个寄存器坍缩到以下状态:

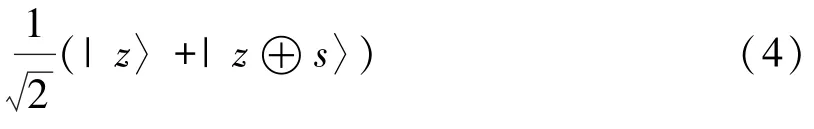
d) 将Hadamard 变换应用于第一个寄存器，得到:

e) 若向量y 满足y.s=1，则| y〉对应的振幅为零。因此，测量该状态得到的向量y 必满足y.s = 0。

执行一次Simon 算法，可测得一个y1与s 正交。再执行一次，可测得另一个y2与s 正交。满足该情况的y 有很多，重复O(n) 次，我们可以得到(n - 1) 相互独立且正交于s 的向量y，通过求解如下线性方程组可得到唯一非零解s。

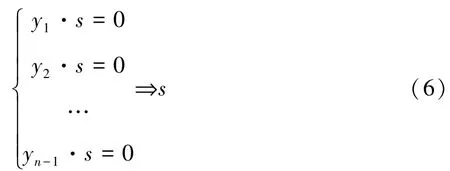
因此对于Simon 问题，Simon 算法的查询复杂度为O(n)，即可在多项式时间内用Simon 算法找到上述函数的周期s。

1.3 周期函数的构造

经典密码中存在各种周期函数的构造。在利用Simon 算法对一个分组密码结构Ek:{0 ，1}n→ { 0 ，1}n进行攻击时，由Ek可以构造一个周期为s 的函数f，攻击者对该函数进行量子叠加态查询，并求出s 从而破解该加密结构。目前基于Ek构造周期函数有以下两种形式:

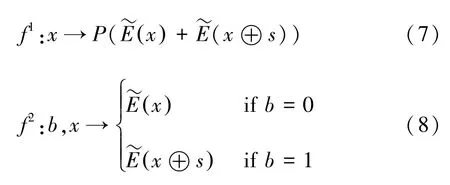
图2 LRW 结构

以Liskov，Rivest 和Wagner 提出的LRW 结构(见图2)为例，由该结构可得加密函数:

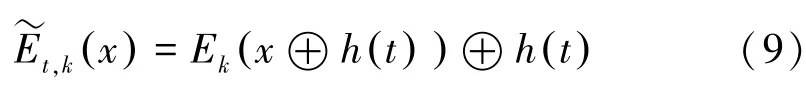
其中t 为参数，与密钥h 有关。接着构造周期函数:

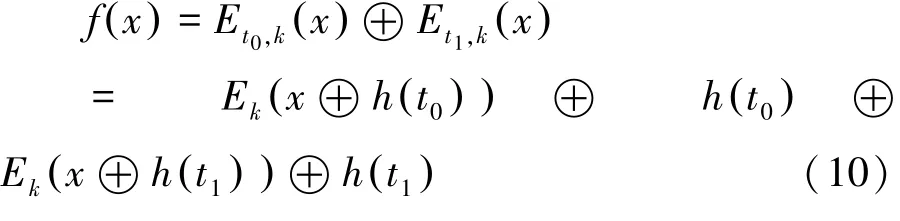
由f ( x) = f ( x ⊕s) ，我们可以得出周期s =h ( t0) ⊕h ( t1) 。

2 对称密码的Simon 量子攻击分析

Simon 算法在对称密码分析中的应用研究思路主要是:利用Simon 算法可以寻找出函数周期且时间复杂度为多项式级别的这一特性，针对对称密码算法构造一系列的攻击方式。首先针对某一对称密码的算法结构、加密模式以及认证加密结构等设计特点，构造相应的周期函数，再利用Simon 算法求解周期，进一步构造区分攻击、伪造攻击、密钥恢复攻击或滑动攻击，实现针对对称密码算法的有效密码分析[1]。

当前关于Simon 算法在对称密码攻击的研究，主要分为以下四种形式:

(1) 量子区分器，需要确定一个oracle 可访问的函数是一个具有特定结构的函数还是一个随机函数。

(2) 密钥恢复，恢复一些可通过oracle 访问的函数所使用的秘密信息。

(3) 滑动攻击，需要函数能够有效识别明密文对中的一个“滑动”对，从而有效地提取函数中密钥。

(4) 量子伪造攻击，攻击者需要在不知道密钥的情况下为任意消息伪造标签，将消息身份验证码破坏。

本节将主要从上述四个方面浅析Simon 算法在对称密码分析中的应用。

规划对临时避险以上级别的绿地全部在控规层面的图纸上进行了四至控制，并对每个防灾避险公园绿地的设施配置和建设要求有了详细的建设指引。既符合上位规划对城市的要求，也能具体指导城市如何建设防灾避险绿地，并达到全覆盖。

2.1 Simon 算法的区分攻击

使用Simon 算法可加速周期函数f 中周期s的搜索过程，因此可应用于密码分析中的区分攻击，用以评估密码的伪随机性。任意给定一个黑盒，它包含以下两种结构中的一种:a.有一定规律的加密结构；b.是随机置换。对黑盒进行访问，判断其结构。若黑盒为加密结构，当该加密结构可以构造出周期函数时，即可利用Simon 算法加速区分攻击。

Simon 算法可对Feistel 结构进行区分攻击。在2010 年的ISIT 会议上，Kuwakado 和Morii 第一个提出Simon 算法在密码分析中的应用[5]，我们知道，没有多项式经典算法能够区分具有内部置换的3 轮Feistel 密码和随机置换(图3 为3 轮Feistel 结构图)。这意味着具有内部置换的3 轮Feistel 密码可以抵抗经典计算机上的任何选择明文攻击。然而Kuwakado 和Morii 证明了量子算法可以区分具有内部置换的3 轮Feistel 密码和随机置换，并提出了针对3 轮Feistel 结构(内部轮函数为置换)的多项式时间内的量子区分器。因此，具有内部置换的3 轮Feistel 密码在量子计算机上的选择明文攻击下可能是不安全的。

图3 3 轮Feistel 结构图

2017 年， Santoli 和Schaffner[6]将上述Kuwakado 和Morii 的结论进行了拓展，将内部轮函数由置换变更为伪随机函数，结论依然成立，即利用Simon 算法可有效区分内部轮函数为伪随机函数的3 轮Feistel 结构与随机置换。

2017 年，Hosoyamada 和Sasaki[7]表明量子计算机可以显著加速Demiric-Seluck 中间相遇攻击，可将6 轮Feistel 结构的区分攻击的复杂度由经典计算的 O(23n/4) 降到量子计算的O(2n/2)。

2019 年Ito 等人[8]同样使用Simon 算法，将Kuwakado 和Morii 的结果扩展了一轮，提出了一个针对4 轮Feistel 结构的量子CCA(选择密文)区分器。

对于广义Feistel 结构，2019 年Dong 等人[9]提出了关于d 分支Type-1 型GFS(广义Feistel结构)的2d - 1 轮的量子区分器，以及2d 分支Type-2 型GFS 的2d + 1 轮的量子区分器。

2019 年罗宜元、闫海伦等人[10]根据MISTY划分的左右结构，求解3 轮MISTY-L 和MISTYR 结构对应的周期函数，从而构造了相应的Simon 量子算法攻击。另外他们还论证了3 轮Lai-Massey 结构在选择明文攻击下，量子攻击者无法构造碰撞函数的周期函数，所以在抵抗Simon 量子算法攻击方面，Lai-Massey 结构与相同轮数的Feistel 结构相比，具有更强的安全性。

2.2 Simon 算法的密钥恢复攻击

EM 密码是Even 和Mansour 提出的一种经典密码[11]，可以看作是AES 的简化版本，如图4。 2012 年Kuwakado 和Morii 在文献[12]中，基于Simon 算法对Even-Mansour 类型的分组密码结构进行量子密钥恢复攻击，给出了1 轮的密钥恢复攻击，证明了在量子计算机上实现的Even-Mansour 密码结构是不安全的。 2017 年Hosoyamada 和Aoki[13]在多项式时间内恢复2 轮Even-Mansour 密码结构的所有密钥，其量子相关密钥攻击是Kaplan 等人[14]的量子滑动攻击的扩展。

图4 EM 密码和AES 模型

在2017 年的Asiacrypt 大会上，Leander 和May[15]结合Grover 和Simon 量子算法来破解基于FX 的分组密码(图5 为FX 结构)，其中使用Simon 算法作为内部判定函数，使用Grover 算法作为外部搜索算法。结果表明在FX 结构中使用白化密钥并不会提高量子CPA 模型的安全性。

2017 年Bonnetain[16]延续Kaplan 等人[14]对AEZ 的分析，提出一个用于发现量子周期的Simon 算法的扩展，对认证加密算法AEZv4 和AEZv5 构造了密钥恢复攻击。

图5 FX 结构，k1，k2 为白化密钥

2018 年，Dong 和Wang[17]首次对Feistel 结构使用量子密钥恢复攻击，结合Simon 和Grover算法，系统研究了针对r 轮Feistel 结构的量子密钥恢复攻击，给出了不同场景下具体的时间复杂度和内存消耗，结果显示该量子攻击的时间复杂度上优于量子暴力搜索算法，同时与最好的经典攻击相比，即Dinur 等人在CRYPTO 2015 的攻击，不仅在时间复杂度上占据优势，还不产生任何额外的内存开销。

2019 年，Ito 等人[8]将他们提出的针对4 轮Feistel 密码的量子区分器扩展到对Feistel-KF 和Feistel-FK 结构进行密钥恢复攻击。

2019 年Dong 等人[11]利用他们提出的Type-1 型GFS 和Type-2 型GFS 的量子区分器，以及Leander 和May 提出的Simon 和Grover 算法结合的方法对Type-1 型、Type-2 型GFS 进行了量子密钥恢复攻击。

2020 年，彭信行等人[18]对6 轮的Feistel 结构进行了密钥恢复攻击，通过对第2 轮和第4 轮的加解密过程构造区分器，得到了4 轮密钥，并给出了该攻击的时间复杂度为2n/2。

2020 年， Dong 等人[19]结合Simon 算法，对全轮的GOST 算法(类似于DES 的分组密码算法)提出了一种新的量子密钥恢复攻击。

2.3 Simon 算法的滑动攻击

在CRYPTO 2016 上，Kaplan 等人[14]通过滑动攻击和Simon 算法相结合，将迭代Even-Mansour 密码的滑动攻击转换为量子攻击。证明了Simon 算法可以应用于滑动攻击，攻击复杂度从O(2n/2) 降到O(n)，是量子模型中经典对称密码分析技术首次实现指数级别的加速。

在2020 年， Dong 等人[19]结合Simon 算法对滑动攻击进行了改进，在多项式时间内破解Feistel 的一些变体，即2K-/4K-Feistel 分组密码以及2K-/4K-DES 分组密码。

2.4 Simon 算法的量子伪造攻击

在密码学中，消息认证码MAC 是经过某特定算法(如hash 函数等)后产生的小段信息，它可以被用来检查信息在传递的过程中是否被篡改。消息伪造攻击就是在篡改明文信息的同时保证篡改后的消息认证码与原来的一致，从而不被发现。 Simon 算法攻击MAC，其本质是找到MAC 函数的周期。

2016 年Kaplan 等人[14]利用Simon 算法对分组密码工作模式进行了量子攻击，有CBCMAC、PMAC、GMAC 工作模式，但是无法攻击CCM 工作模式。对于CBC-MAC 构造周期函数为:

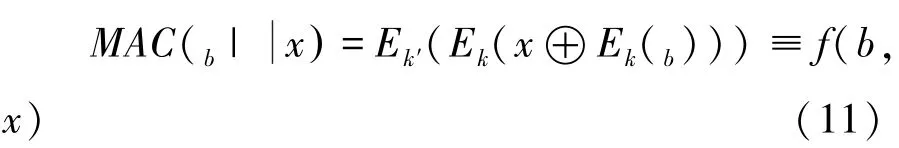
由f ( b，x) = f ( b′，x′) x ⊕ Ek(b) = x′ ⊕Ek(b′) ，求得周期s=1|| Ek(0) ⊕Ek(1) 。同理可以求得PMAC、GMAC 工作模式的MAC 函数的周期。另外Kaplan 等人[14]还提出Simon 算法可以对GCM、OCM 模式(当输入消息为空时)以及对凯撒密码的候选算法，如CLOC、AEZ、COPA、OTR、POET、OMD、Minalpher 等进行攻击，复杂度仅为O(n)，其中n 是块的大小。他们证明了一些认证和认证加密方案在量子环境下是不安全的。

2017 年，Santoli 和Schaffner[6]提出了针对消息认证方案CBC-MAC (固定长度消息)加密模式的量子伪造攻击。其攻击也适用于将基本CBC-MAC 扩展到任意长度的消息，方法是在消息长度之前加上前缀。

2017 年Bonnetain[16]，证明了AEZ 的所有版本都在量子叠加模型中被严重破坏，不仅对AEZv4 和AEZv5 进行了密钥恢复攻击，并用于对AEZ10 的伪造攻击，其复杂度远低于设计者所提出的。

3 对称密码抗Simon 算法量子攻击的方法

能有效抵抗经典计算机攻击，又能抵御已知量子计算攻击的密码算法，称为后量子密码(Post-Quantum Cryptography，简称PQC)，或称为抗量子密码 ( Quantum-resistant Cryptography)[20]。 2016 年美国国家标准与技术研究院NIST 启动了全球范围内的后量子密码算法的征集工作。作为未来代替RSA、Diffie-Hellman、ECDH 等现行公钥密码算法的密码技术，后量子密码正被越来越多的人所知。后量子密码的研究主要在公钥体制，在对称密码体制研究较少，当前主流的后量子密码体制有四种类型[21]:基于hash、基于编码、基于格、基于多变量的密码体制。上节所叙述的量子算法在对称密码体制的研究结果表明许多经典密码的安全证明需要从量子攻击者的角度被重新审视，也为经典密码学的后量子密码安全性提供了新的思路。

结合Simon 量子算法的攻击特点，经典对称密码可以考虑以下几种方法增强自身安全性，提高抗Simon 量子算法攻击能力。

(1) 增加密钥长度

对于对称密码算法，并不急切需要新算法代替，因为可以通过调整参数解决。正如前文所提到的，Grover 算法提高了密钥空间的搜索效率，能够应用于许多密码体制的量子计算攻击，其效果相当于将分组密码的密钥长度降低了一半。因此，通过增加一倍的密钥长度，可以抵抗这种攻击。这种方法对密码安全性的提升是建立在增加系统资源消耗，牺牲效率的基础上，并非最佳策略。

(2) 采用量子网络编码

利用量子不可克隆原理的量子网络编码可有效防止信息被窃听。 1982 年，Wootters 和Zurek[22]提出了量子不可克隆原理，即在量子力学系统中，一个未知量子态不可能被全部准确克隆。如果用于编码的量子态中包含非正交态，当窃听者通过量子操作来获得关于编码的信息时，根据量子不可克隆原理，接收方所收到的量子态和发送方原始配置的量子态就会不同，于是导致其统计特性发生变化，从而使窃听被通信双方察觉[23]。

(3) 采用量子密钥分发(QKD)

当前“利用公钥算法分发对称密钥，然后基于对称密钥加解密信息”的混合方案在密码系统得到了广泛应用。通过QKD 代替公钥算法可保证对称密钥的安全分发。 QKD 利用量子力学特性保证通信安全。其最重要也最独特的一个特性就是通信双方可以察觉到第三方的窃听。并且量子力学是物理定律，可以被认为是永久有效的，这使得量子密钥分发能够提供长期的安全保障性。