磁流变阻尼器Bouc-Wen模型参数辨识研究
2021-04-06杨永刚丁有闯
杨永刚,丁有闯
(中国民航大学航空工程学院,天津300300)
目前,磁流变阻尼器(MRD,magneto-rheological damper)以其性能良好、耗能少、结构简单、响应速度快、阻尼力大且可调等优点,广泛应用于航空、汽车、建筑等领域[1]。但由于磁流变阻尼器动力学模型的滞回特性,使得其数学模型非常复杂。为精确有效地实现阻尼器输出阻尼力的控制,必须保证模型的精确性和有效性。
常见磁流变阻尼器模型有Bingham 模型、修正的Dahl 模型、Bouc-Wen[2]模型、双曲正切模型[3]等。其中Bouc-wen 模型是最典型的模型之一,但该模型的待识别参数多达8 个,因此,模型参数的精确识别具有重大意义。为此,国内外学者对磁流变阻尼器模型的参数辨识做了大量研究。Peng 等[4]虽然利用Matlab 工具箱识别出了Bouc-Wen 模型参数,但并未对识别出的参数结果进行检验和证明。Talatahari 等[5]有效引入了一种基于帝国竞争算法(EICA,enriched imperialist competitive algorithm)的优化方法来处理Bouc-Wen 模型非线性优化问题,但不适用于其他模型。Yang 等[6]对磁流变阻尼器进行了性能试验及力学模型分析。王修勇等[7]采用粒子群算法对磁流变阻尼器模型进行了参数识别,但迭代次数过大,寻优过程繁琐。胡海刚等[8]在试验数据基础上,采用1stopt 软件的通用全局优化算法(UGOA,universal global optimization algorithm)识别出Bouc-Wen 模型参数,但识别精度不高。文献[9-12]首先利用遗传算法对参数化模型进行了参数识别,但该算法对计算机内存和CPU 运算速度要求较高;然后基于模型参数识别法、遗传算法及模式搜索法对Bouc-Wen 模型进行参数识别,但该过程过于复杂。
鉴于以上辨识方法具有过程复杂、识别精度不高等缺点,提出一种基于Matlab/Simulink 辨识工具箱的最小二乘法对Bouc-Wen 模型进行参数识别。首先利用磁流变减摆器力学性能试验数据,在Simulink 中搭建Bouc-Wen 模型,其次利用Parameter Estimation 工具箱,选择非线性最小二乘法迭代算法对模型参数进行了辨识,并结合参数的物理意义对识别结果进行分析,确定随电流变化参数,进而确定所有参数辨识结果。最后采用其他幅值频率的试验数据对Bouc-Wen 模型进行验证,结果表明,试验结果和仿真结果拟合度较高,该参数模型能较好地描述阻尼力的滞回特性。
1 磁流变阻尼器力学性能试验
磁流变阻尼器力学性能试验在拉伸试验台上进行,磁流变减摆器[13]结构原理图如图1所示。实验平台利用激振器产生的不同频率幅值信号及直流电源为夹持的磁流变减摆器提供的电流,产生阻尼力和活塞杆位移等参数的数据变化。其中,激励信号为正弦信号x=Msin(2πft),幅值M=10 mm,频率f=0.4 Hz,电流强度分别取为0、0.25、0.50、0.75、1.00 A。各种工况下功量图与试验数据处理得到的位移-阻尼力和速度-阻尼力曲线图如图2~图3所示。
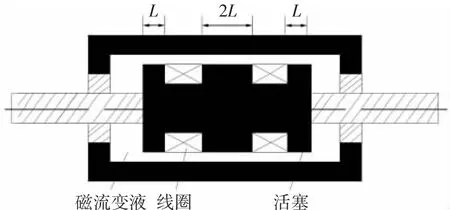
图1 结构原理图Fig.1 Structural schematic diagram
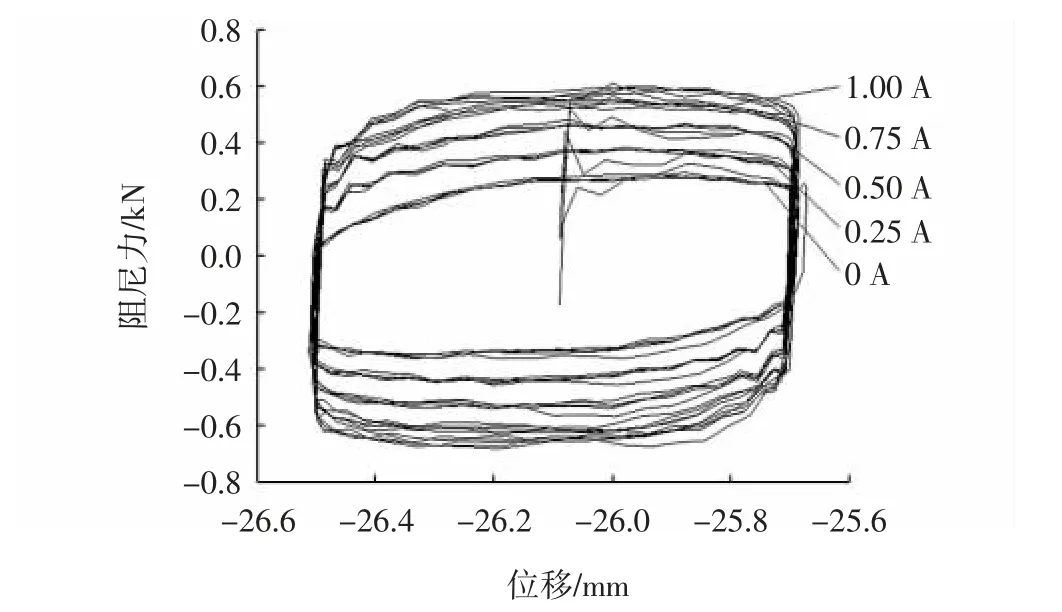
图2 位移-阻尼力曲线Fig.2 Curve of displacement-damping force

图3 速度-阻尼力曲线Fig.3 Curve of velocity-damping force
2 Bouc-Wen 模型
Bouc-Wen 模型虽然在数学表达式上复杂,但其易于处理且能较好地描述磁流变阻尼器在低速区的非线性滞回特性和能耗性,因此,该模型可用来做磁流变阻尼器阻尼力模型。Bouc-Wen 模型简图如图4所示。
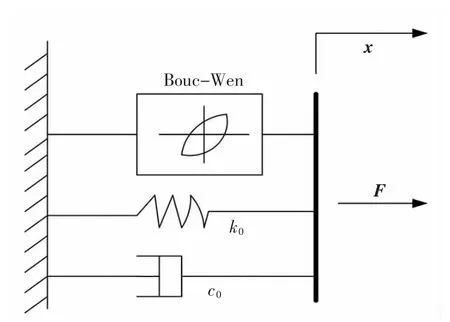
图4 Bouc-Wen 模型Fig.4 Bouc-Wen model
其微分方程表达式为
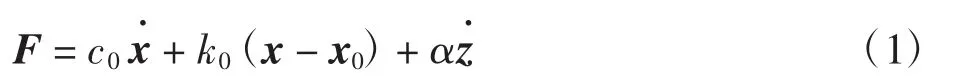
式中:F 为磁流变阻尼器产生的阻尼力;c0为磁流变液阻尼系数;k0为刚度系数;x 为位移;x0为初始位移;α为滞回变量的系数;滞回变量为
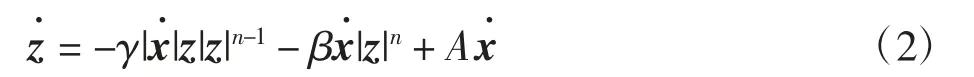
式中:n 为曲线圆滑系数;γ 为滞回模型的宽度调节系数;β 为滞回模型的高度调节系数;A 为比例系数。
在Simulink 环境下搭建的Bouc-Wen 模型如图5所示。

图5 Simulink 环境下搭建的Bouc-Wen 模型Fig.5 Bouc-Wen model built in Simulink environment
3 参数辨识
3.1 非线性最小二乘法
非线性最小二乘法是最小二乘法的分支,可用来估计非线性模型参数。其原理是通过求取误差平方和的目标函数Q 的最小值,从而得到对所估计目标函数的最优解。
设所辨识模型的数学表达式为

式中:y 为系统的输出;x′,x″,…为输入;θ′,θ″,…为参数。在估计参数时模型的数学表达式f 是已知的,经过实验取得数据为(x1′,x1″,…,y1),(x2′,x2″,…,y2),…,(xn′,xn″,…,yn)。
非线性模型误差平方和的目标函数Q 为
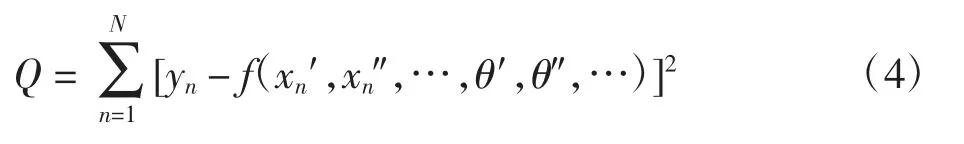
3.2 Bouc-Wen 模型的参数辨识
Bouc-Wen 模型的参数达8 个,使用遗传算法、粒子群优化算法等识别方法代码繁琐,比较复杂。使用基于Matlab 最小二乘法的迭代算法,利用试验数据自动调用迭代算法,使试验值和仿真值无限接近,达到辨别所有参数的目的。辨识流程图如图6所示,具体步骤如下:
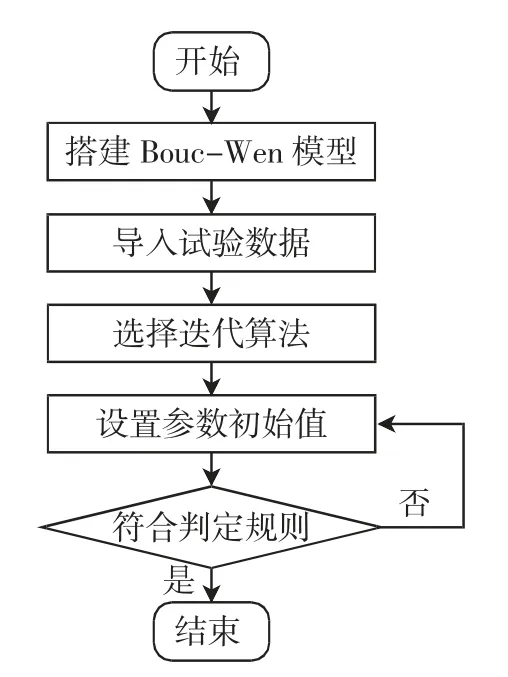
图6 辨识流程图Fig.6 Identification flow chart
1)利用已搭建的Bouc-Wen 模型,通过Parameter Estimation 工具箱导入试验数据,输入数据为位移和速度,输出数据为阻尼力;
2)根据经验,设定初次辨识的参数初始值分别为:α=30 N·mm-1、β=-500、γ=800、n=2、x0=-26 mm、k0=300 N·mm-1、A=1 000、c0=80 N·s·mm-1。确定辨识范围,最后数据上传模型;
3)点击option 选择优化选项,选择最小二乘法迭代算法,代价函数选择和平方差,最后点击Estimation进行参数估计。计算机会根据试验曲线和仿真曲线的接近度根据判定规则停止参数估计。辨识结束后的试验值与仿真值拟合图如图7所示。参数辨识结果数据如表1所示。
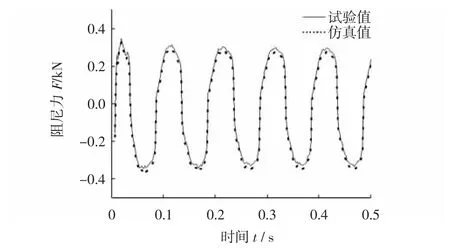
图7 试验值和仿真值的曲线拟合Fig.7 Curve fitting between test and simulation value
由表1可知,不论是试验值还是理论值,n 和x0都近似为常数值,因此取其平均值n=1.01、x0=-25.64 mm作为下次参数识别的初始值。由于参数A、β、γ 是滞回模型的调节系数,在对误差平方和最小的追求中,A、β、γ 相较于α、c0、k0更容易实现调节。同时在表1中可发现,由于采用第一次参数估计后得出的参数值作为下次参数估计的初始值,存在着迭代关系,所以表1中后3 组的A、β、γ、k0值受电流影响较小,更具参考意义,因此将结合后3 组的数据采用逐步缩小边界法再次进行参数识别。因此接下来要识别6 个参数,因此减小了识别难度。以首次辨识电流为0.5 A 时识别出的参数为初始值,辨识结果如表2所示。
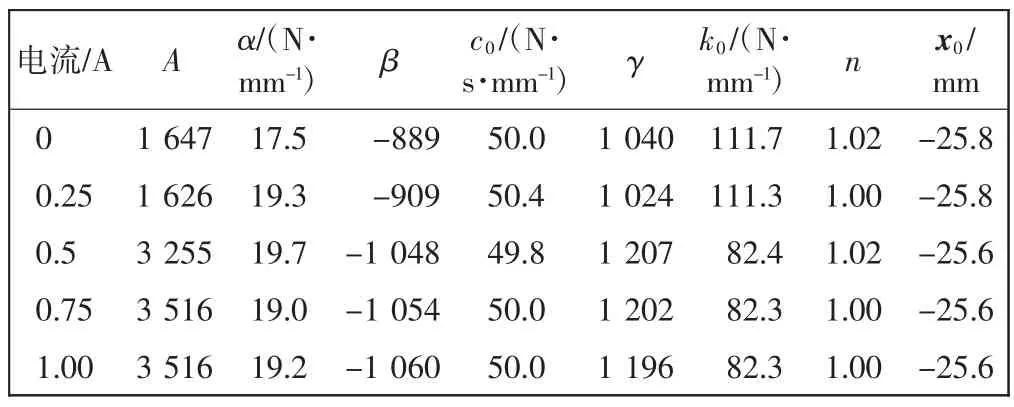
表1 各参数的辨识结果Tab.1 Identification result of each parameter
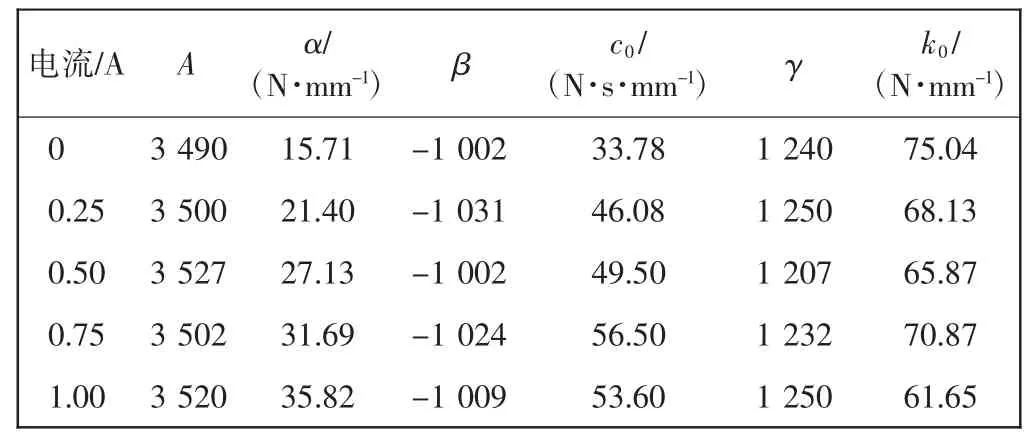
表2 缩小辨识边界范围的辨识结果Tab.2 Identification result with reduced boundary range
由表2可以看出参数A、β、γ、k0变化幅度不大,可以其平均值作为其模型的识别后参数,A = 3 507.8、β=-1 013.6、γ=1 235.8、k0=68.31 N·mm-1。α 和c0随电流变化而有规则地变化,因此即可认为α 和c0与电流有以下关系

借助Matlab 曲线拟合工具箱(curve fitting tool),拟合结果如图8所示,可得出α1、α2、c1、c2、c3。
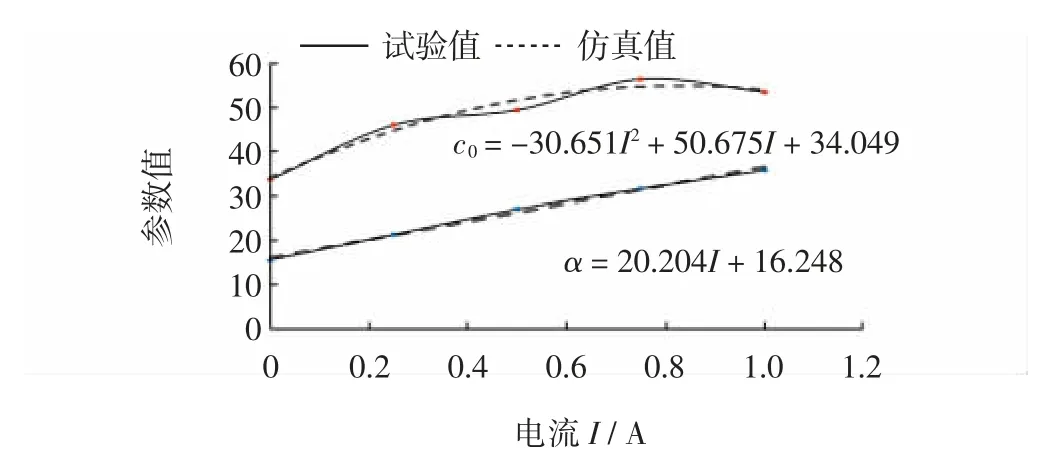
图8 α、c0 曲线拟合Fig.8 Curve fitting between α and c0
因此,由拟合结果可知α1= 20.204 N·mm-1、α2=16.248 N·mm-1、c1=-30.651 N·s·mm-1、c2=50.675 N·s·mm-1、c3= 34.049 N·s·mm-1。至此最终辨识结果为:α1= 20.204 N·mm-1、α2= 16.248 N·mm-1、c1= -30.651 N·s·mm-1、c2=50.675 N·s·mm-1、c3=34.049 N·s·mm-1、A=3 507.8、β=-1 013.6、γ=1 235.8、k0=68.31 N·mm-1、n=1.01、x0=-25.64 mm。
4 模型验证
为了验证辨识参数结果的正确性,在辨识模型基础上增加一个可发出随时间变化正弦信号的模块组代替输入模块x,输入数据由变量改为辨识后得出的参数常量,c2、α 作为电流I 的函数输入,将输出模块数据导入工作空间,得到了仿真模型如图9所示。

图9 参数验证仿真模型Fig.9 Parameter verification simulation model
将上述辨识结果代入仿真模型,首先验证同幅值频率的任意电流下的仿真输出数据与试验数据的吻合程度。位移-阻尼力的仿真试验对比图和速度-阻尼力的仿真试验对比图如图10所示。
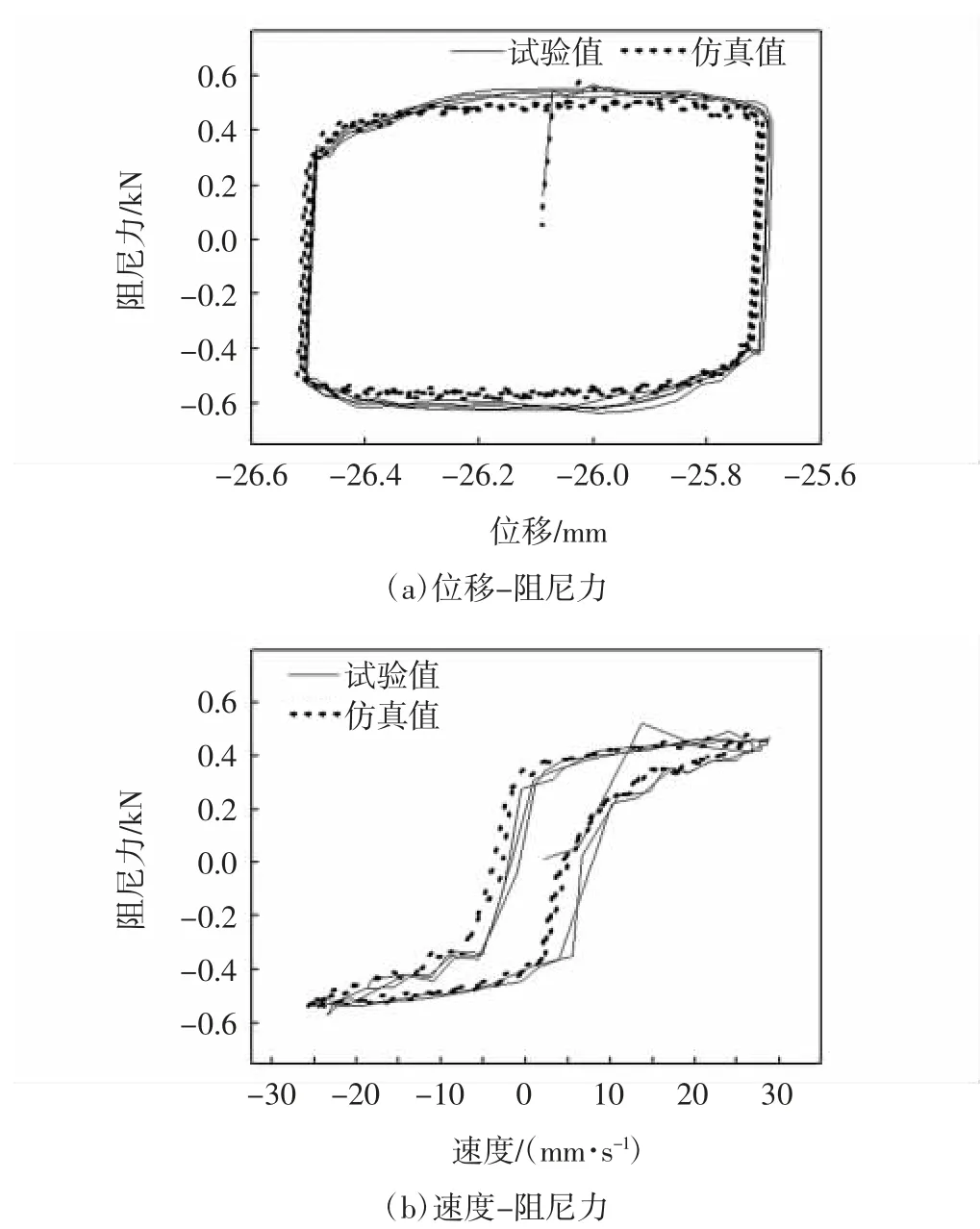
图10 0.4 Hz、10 mm、0.5 A 条件下的仿真试验Fig.10 Simulation experiment diagram under 0.4 Hz,10 mm,0.5 A
由图10可知,位移-阻尼力仿真试验图以及速度-阻尼力仿真试验图吻合度较好,验证了参数辨识结果的正确性。为了验证基于Matlab/Simulink 辨识工具箱——最小二乘法方法的正确性和通用性,再随机选取不同幅值频率的数据来进行验证,如图11所示。
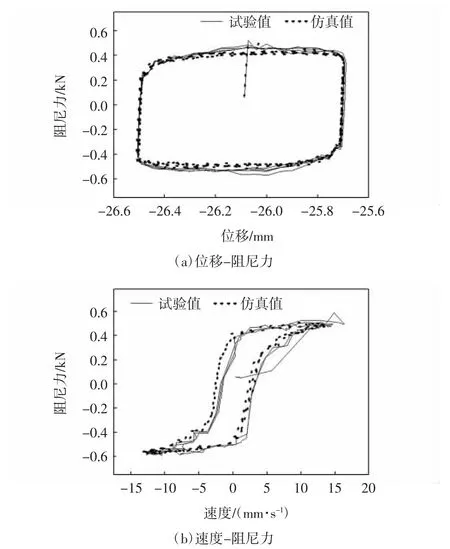
图11 0.7 Hz、7.5 mm、0.5 A 条件下的仿真试验Fig.11 Simulation experiment diagram under 0.7 Hz、7.5 mm、0.5 A
由图11可知,选取0.5 A,频率为0.7 Hz,幅值为7.5 mm 的数据进行验证,也能较好地反映辨识结果的正确性以及该动力学模型的通用性。
5 结语
首先在Simulink 中搭建Bouc-Wen 模型,然后利用在拉伸试验台上做的阻尼器力学性能试验数据,基于Parameter Estimation 工具箱使用非线性最小二乘法迭代算法对Bouc-Wen 模型进行参数识别,最后搭建仿真验证模型对参数辨识结果进行验证。得出结论如下:
1)辨识出的Bouc-Wen 模型参数不仅能很好地与参与辨识的数据相吻合,而且还能较好地表达阻尼器其他幅值频率下的动力学特性;
2)辨识出的模型各参数物理意义清晰,有助于进行下一步的减摆器控制工作。使用非线性最小二乘法,算法效率高,易于实现,对于其他阻尼器模型参数辨识也具有通用性。
