基于时间容差的内切转弯飞行状态符合性评估

吴仁彪，安 丽，张 喆，王 鹏

（中国民航大学天津市智能信号与图像处理重点实验室，天津 300300）

在民航运输过程中，为了确保航空运行安全及效率，飞行前科学制定飞行计划，执行阶段严格实施，飞行结束后分析评价是确保飞行安全和高效的重要环节[1-2]。尽管在飞行前已经对飞行计划进行审批[3]，但实际飞行过程中，由于天气、导航、飞行操作等随机因素的影响，实际航迹与飞行计划航迹之间不可避免地存在偏差[4-6]，过大的偏差将影响飞行安全与效率。飞行计划符合度评估是对实际飞行航迹与计划航迹之间的偏差程度进行评估，在空中交通管理、航空公司运行监控、飞行品质分析等民航运行安全保障领域具有十分重要的作用[7-9]。

现有评估方法通常是基于距离的度量，即通过将时间、速度等因素加权转化为距离，再使用单一距离门限判断该距离是否在门限范围内。Reynolds 等[10]采用故障分析模型，通过将实际航迹与计划航迹间多个特征值的差异加权综合后，再与单一距离门限比较，评估实际运行是否与计划相符合。贺文红[11]基于模型的故障检测与分离技术研究飞机状态符合性问题。孙石磊等[12]基于动态时间弯曲的距离度量方法计算航迹到聚类之间的距离，再与单一距离门限比较，提升了单一距离门限评估的稳健性。基于距离的度量方法将航迹偏差在整条航迹范围内进行平均，故上述方法适用于评估飞行状态比较稳定的航迹。而对于机动飞行较多的情况，实际飞行航迹与计划航迹可能存在较大差异，单一距离门限评估无法针对飞行状态变化进行动态调整，故难以实现对机动飞行场景的有效正确评估。

针对此问题，通过对实际飞行存在的合理航迹偏差进行建模，选取内切转弯为机动飞行场景作为研究对象，提出了一种基于时间容差的内切转弯飞行状态符合性评估方法，克服了使用单一距离门限评估机动飞行符合性的局限性。

1 内切转弯模型

在飞行过程中，常见转弯方式[13]包括内切转弯（flyby）和飞越转弯（fly-over）。内切转弯是指转弯航迹由固定半径的圆弧和与之相切的前后两个直线航段组成的转弯；飞越转弯是指航空器在航路点开始转弯，转弯航迹由两段固定半径的圆弧和与两圆弧分别相切的一段直线段组成。两种转弯方式如图1所示。由于飞越转弯需要进行改入转弯和改出转弯，且两次转弯坡度不同，而内切转弯只需要一次固定半径的转弯且更容易操作，航路上最常用内切转弯，因此，选取内切转弯作为研究对象。

图1 转弯方式Fig.1 Turning mode

1.1 理想内切转弯模型

考虑水平飞行时处于理想无风状态，飞机转弯半径R 由坡度角φ、转弯速度v、重力加速度g 确定，关系如下

式中，飞机的极限性能限制了坡度角的最大值φmax，因此，在转弯速度v 一定的情况下，内切转弯存在最小转弯半径Rmin。

图2展示了一个典型的水平内切转弯过程：WP1、WP2、WP3为飞行计划中的3 个航路点，飞机需在WP2附近实施转弯以从WP1—WP2转至WP2—WP3运行，WP1—WP2航段与WP2—WP3航段的航向角变化为θ，WP1—WP2距离为s1，WP2—WP3距离为s2。

对于转弯半径R 的内切转弯过程，A、B 分别为转弯圆弧与两航段航路的切点。在该模型中，以A 为理想内切转弯起始点，B 为结束点。A 到WP2距离为d，与转弯半径R 的关系表示如下

图2 内切转弯飞行示意图Fig.2 Schematic of fly-by turning

内切转弯模型中的飞行时间以飞越WP1航路点的时刻作为起始时刻。设飞至点A（x0，y0）时刻为t1，则转弯过程中任意时刻t 飞机所在位置P（x，y）坐标表示如下

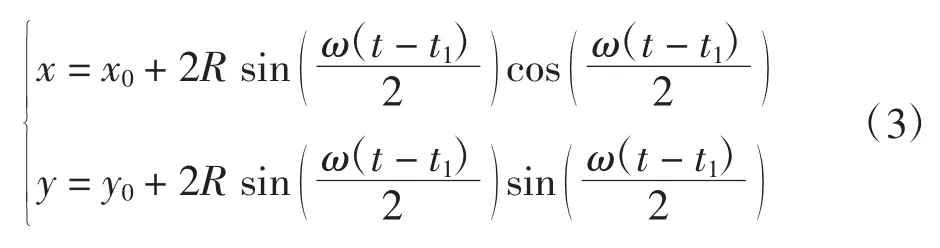
1.2 考虑时间容差的内切转弯模型

考虑实际飞行活动中存在操作、导航等误差因素，转弯起始时刻t1具有不确定性，一个合理的假设是t1服从正态分布t1～N（μ，σ2），则转弯起始点位置A（x0，y0）的概率密度为

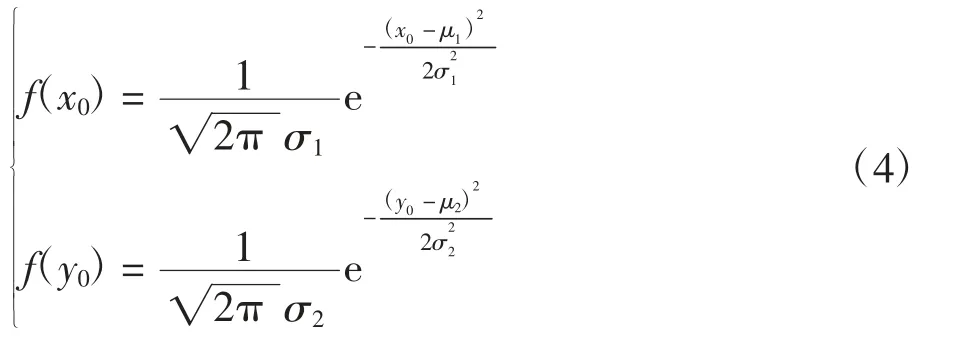
其中

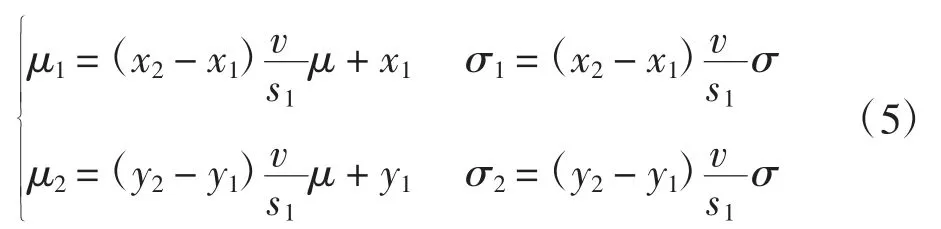
式中，（x1，y1）、（x2，y2）分别为航路点WP1、WP2的坐标。

在转弯过程中，t 时刻飞机所处位置P（x，y）的分布由t1时刻位置的概率分布决定。

一个典型的通用航空器内切转弯飞行场景如图3所示。以WP1航路点为坐标原点，建立平面直角坐标系。据此转弯处多条实际飞行航迹的统计结果，飞机转弯速度v 取255 km/h，内切转弯起始时刻t1（单位：s）服从N（400，900）的正态分布。

图3 考虑时间容差的理想内切转弯示例Fig.3 Schematic of ideal fly-by turning considering time tolerance

2 飞行状态符合性评估

由于转弯运动是非线性运动，因此，使用Monte Carlo 方法确定P（x，y）的分布规律，得到不同时刻同一空间尺度区域上的位置分布。由于模型中考虑了起始状态时刻的容差，转弯过程中合理位置分布的范围也因此得到扩展，需使用不同门限评估飞行状态符合度，以提高评估结果的准确性与稳健性。

2.1 位置分布符合度门限

在一定的精度范围内使用圆形区域表征具有某一给定位置分布概率的区域，以下称为位置分布圆域。在对算法实时性要求较高的场景中，可使用位置分布圆域近似代替非规则形状的给定概率分布区域。

使用Monte Carlo 方法计算转弯飞行t 时刻所在位置分布圆域，步骤如下：首先确定内切转弯起始时刻位置分布并生成随机数，然后输入到转弯运动模型中计算t 时刻飞机位置；重复进行n 次独立Monte Carlo 实验，计算n 次位置的中心及给定概率下的圆域半径。t 时刻转弯位置分布圆域计算流程如图4所示。

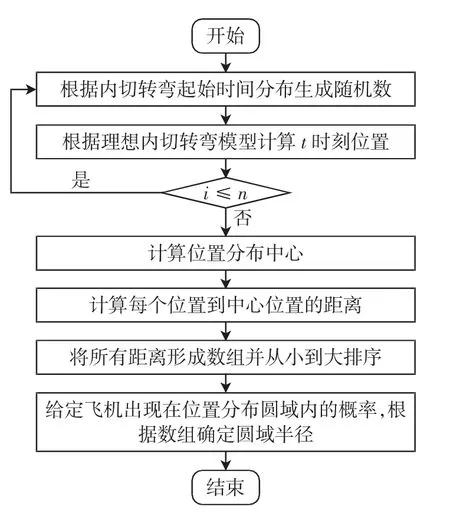
图4 t 时刻转弯位置分布圆域计算流程Fig.4 Computing process of circular region of turning position distribution at time t

具体计算过程如下。

1）t 时刻飞机所处位置计算

设第i 次Monte Carlo 仿真中，内切转弯起始位置为A（x0，y0），飞行速度为v，t 时刻飞机所处位置为P（x，y），具体步骤如下：

步骤1根据内切转弯起始时刻位置分布生成随机数，计算第i 次仿真转弯起始位置A（x0，y0）；

步骤2利用生成的A（x0，y0）坐标，根据式（2）计算理想内切转弯半径R；

步骤3根据理想内切转弯模型，据式（3）计算飞行t 时刻所在位置P（x，y）。

2）位置分布中心计算

经n 次Monte Carlo 仿真得到n 个位置构成数组{P（x1，y1），P（x2，y2），…，P（xn，yn）}，计算n 次位置的中心C（xcenter，ycenter），即

3）圆域半径计算

用圆域表征飞机位置分布区域，计算圆域半径R。圆域内的概率P 是一定的，给定概率P=95%下的圆域，即t 时刻飞机位置出现在该圆内的概率为95%。半径R 计算步骤如下：

步骤1遍历n 个位置P（xi，yi），分别计算其到中心位置C（xcenter，ycenter）的欧式距离di，即

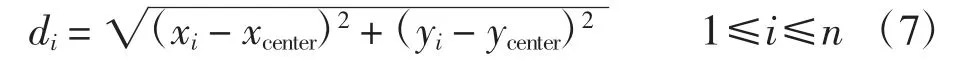
步骤2将n 个距离di按照递增排序后，构成一个有序数组{d1，d2，…，dn}；

步骤3根据给定概率P，确定圆域半径在数组{d1，d2，…，dn}中的位置，即可得到半径值R，计算方法为

式中，ceil（·）表示向上取整。

2.2 评估流程

飞行状态符合性评估流程如图5所示，步骤如下。

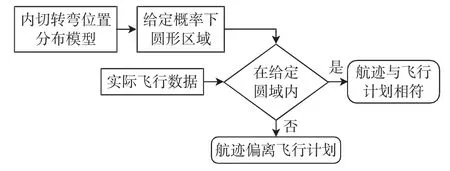
图5 飞行状态符合性评估流程Fig.5 Flight status conformance assessment process

1）建立位置模型 建立内切转弯模型，计算t 时刻航空器位置。

2）确定位置分布圆 使用Monte Carlo 方法模拟t时刻航空器所在位置分布，计算给定概率（如95%）下的圆域范围。

3）符合性判决 以所给定概率下的圆域作为门限，评估实际航迹的飞行状态符合性，当观察时刻航空器航迹位于圆域范围内时，实际航迹与飞行计划满足预设的符合度要求；否则认为该航迹的飞行状态偏离相应飞行计划，需进一步处理以确认是否需要产生告警。

3 实验结果分析

实验数据采用2019年10月27日—12月30日美国LAS-SFO 航班ADS-B 飞行数据[14]，机型包括B737 和A320，航迹点标称更新间隔为30 s。

测试数据为该航班的200 条实际飞行航迹，测试场景为在SHEAD—BIKKR—DYAMD 段的内切转弯。以相邻航迹点对应的航向角改变超过5°为转弯起始与结束的判别标准。经统计分析可知：起始转弯时刻均值为414.0 s，标准差为108.2 s。其中，典型的4 条转弯航迹如图6所示。实验中使用UTM 投影将经纬度坐标转为平面二维直角坐标[15]，坐标原点对应经纬度为（32°N，120°W）。

图6 实际飞行内切转弯航迹示例Fig.6 Examples of actual fly-by turning trajectory

现行空管自动化系统中偏航告警通常采用文献[10]中使用的单一距离门限评估方法，该类方法在计划航迹两侧定义了固定宽度的区域，其边界表示允许偏离的距离门限，一旦航空器越界，即判定实际航迹偏离原飞行计划。按照现有航路区域设置规定[16-17]，国内航路宽度为20 km，国际上为10 n mile（1 n mile =1 852 m）。验证实验中单一门限方法的航路宽度取10 n mile。

3.1 准确性验证

以测试数据中与飞行计划航迹距离最相近的实际航迹[18]为例，说明所提方法在提升评估准确性与稳健性方面的优势。

图7中执飞机型为B737，转弯速度为849.2 km/h，在401 s 时开始水平转弯飞行。考察转弯起始到结束之间的航迹，选取转弯起始时刻与该时间段的中间点时刻作为观察时刻，即t=401 s 和t=665 s 时刻的飞行状态符合度，所提方法和单一距离门限评估方法对实际航迹的评估结果如图7所示。

图7 不同时刻下方法的准确性对比Fig.7 Accuracy comparison of two methods with different t

图7（a）中，在观察时刻t=401 s 时，实际航迹位置处在10 n mile 边界范围内，同时位于95%圆域范围内，所以两种方法都判决为该时刻实际飞行状态与计划符合；图7（b）中，在观察时刻t=665 s 时使用单一距离门限方法得到实际航迹发生了越界偏离，判决该航迹的实际飞行状态偏离飞行计划，而所提方法得到实际飞行位置仍处在95%圆域内，判定为实际飞行状态与计划满足预设的符合度。图7中两圆域半径依次为4.30 km、14.7 km，可看出，位置分布在转弯飞行不同阶段具有不同的范围，表明所提方法可有效反映出内切转弯飞行各个时间段内偏离程度的变化，提高了评估结果的准确性与稳健性。

3.2 预警时间验证

以测试数据中一条提前转弯的实际航迹[19]为例，说明所提方法在提前预警时间方面的优势。

图8中执飞机型为B737，转弯速度为880.7 km/h，在292 s 时开始做水平转弯飞行。考察转弯起始时刻与飞机位置刚处于10 n mile 航路边界之间的过程：选取该时间段的中间点时刻及飞机位置位于10 n mile航路边界时刻作为观察时刻，即t=326 s 和t=360 s时刻的飞行状态符合度，所提方法和单一距离门限评估方法对实际航迹的评估结果，如图8所示。

图8 不同时刻下方法的预警时间对比Fig.8 Warning time comparison of two methods with different t

图8中的实际航迹，使用单一距离门限评估方法对飞行状态偏差的预警时刻为t=360 s。从图8可看出：时刻t 在326 ～360 s 时段内，由于实际航迹位置未超出设定的10 n mile 边界范围，使用单一距离门限评估方法不会检测到飞行状态偏差；而所提方法均能够检测到飞行位置不在95%圆域内，判定为实际飞行状态偏离飞行计划。

实验结果表明，所提方法能够有效识别机动飞行中的状态变化，对不符合计划的飞行状态能够有效提前预警时间。由于所提方法能够在转弯飞行过程中自动合理地设置各时间段内的符合度门限，有助于提升飞行活动的安全性。

4 结语

针对一般单一距离门限评估方法在转弯飞行中无法有效识别飞行状态改变的问题，提出一种基于时间容差的内切转弯飞行状态符合性评估方法。通过引入时间容差，实现对内切转弯过程中飞行状态变化的合理建模，能够有效反映内切转弯飞行阶段内位置偏离程度的变化。在实际飞行航迹进行验证，结果表明所提方法对机动飞行中飞行状态的改变具有提前预警作用，并能够有效提升评估结果准确性与稳健性。