基于微分博弈的群智频谱感知算法

胡 敏，朱 琦

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

0 引 言

近年来，认知无线电成为减轻拥挤无线电频谱的有效技术，通过动态的频谱接入，可以大大地提高现有频谱资源的利用效率[1-2]。认知无线电的关键技术是频谱感知，认知设备(即次用户)感知到主用户的空闲频谱后可以以机会式的方式动态接入。一般将频谱感知方法技术分为发射机检测、协作检测和基于干扰的检测[3]，由于受阴影效应和深度衰落影响，单节点感知结果不准确，因此需要多个节点协作感知来提高检测可靠性。随着当前科学技术的快速发展和学习模式的巨大改变，人们对移动通信方面的需求大大增加，而计算机技术是这一需求的依靠。新形势下的移动通信技术其实是依靠计算机技术和通信设备将信息数据进行传输，再经过信息处理实现资源共享和其余的服务。

计算机通信技术是计算机技术和通讯技术的融合，应用于实时远程通信、多媒体技术应用和无线计算机通信技术等。计算机通信技术的原理是把信息转换为数据，通过数据的方式传递信息[4]。

文献[5]中使用基于能量检测和特征值检测的两种频谱感知技术来判断信道是否空闲，通过能量检测的方法推导了频谱感知中检测概率和虚警概率的表达式，并研究了在主用户得到充分保护的约束下，优化感知时间来最大化网络的吞吐量。文献[6]通过利用次用户的空间分集来提高频谱感知性能。文献[7]提出了一种分布式协作算法，两个次用户进行合作，其中一个次用户距离主用户较近，感知准确性较高，另一个次用户离主用户较远，这样就不需要集中机制就可以配对次用户。

以上研究都是假设用户均愿意参与感知任务，但是由于感知频谱需要消耗用户终端的资源，因此需要采用一定的激励机制来激励更多的次用户参与感知。

群智感知可以利用大量的移动设备共同提供某类感知信息，广泛应用于交通监控、环境监控、城市安全等领域[8]。文献[9]提出了基于斯坦伯格博弈的方法来激励移动用户的参与，并使用后向归纳来分析群智感知平台的最优激励机制。文献[10]提出了一种基于反向拍卖的激励机制，并在初始激励中采用Vickrey-Clarke-Groves(VCG)机制，使得竞价成为最终激励机制中的主导策略。

文献[11]提出了一种基于随机博弈的激励机制，该机制针对用户行为的不确定性，通过确定任务参与者级别，为参与者设计策略来选择合适任务，并保证参与者的最低收益。文献[12]设计了一种新颖的基于逆向拍卖的动态定价激励机制，提出的激励机制侧重于最小化和稳定激励成本，同时通过防止用户退出参与感知来保持足够的参与者水平。文献[13]设计了一种基于反向拍卖的激励机制，其目标是通过优化系统中人员的组成来最大程度地减少系统维护成本(包括拍卖成本和招聘成本)。以上研究都没有将群智感知应用到具体场景。

该文将频谱感知和群智感知相结合，设计了一种基于微分博弈的群智频谱感知算法。将平台的效用定义为第三方支付的报酬减去付给次用户的报酬，次用户的效用定义为平台支付的报酬减去次用户参与频谱感知任务的花费，平台决定任务的价格，各个次用户决定对任务的检测概率，以获得各自效用最大为目标设计了一种非合作的微分博弈模型，通过求解反馈纳什均衡推导证明了平台和用户的最优策略。微分博弈是指在时间连续的系统内，多个参与者进行持续的博弈，力图最优化各自独立、冲突的目标，最终获得各参与者随时间演变的策略并达到纳什均衡，即任何参与者都没有单独改变策略的意愿，其状态的演化由微分方程描述。

1 系统模型

文中的系统模型如图1所示，平台发布频谱感知任务，次用户根据发布的任务对频谱进行感知。假设次用户数为N，各个次用户均可以通过能量检测感知主用户频段，得到相应的检测结果和检测概率，次用户将相关信息通过基站发送到平台。相关信息被转化成数据在计算机之间进行传递，移动通信技术与计算机技术相互促进推动，逐渐融合。

图1 系统模型

检测概率是频谱感知的重要参数，用户i(i=1,2,…,N)能量检测的检测概率为[14]：

(1)

其中，Pf表示虚警概率，即当主用户不存在时次用户误判主用户存在的概率，τi为次用户i的感知时间，fs为采样频率，τifs则是采样点数，SNRi表示次用户i接收主用户发送信号的信噪比，Q函数为互补累计分布函数：

(2)

平台和用户之间存在价格和检测概率的博弈，用户通过完成任务获得收益，其获得的收益与检测概率成正比，由式(1)可以看到，当信噪比一定时，获得的检测概率与检测时间有关，检测时间越长，则检测概率越高，但是用户付出的代价越大，因此用户需要确定最优的检测时间(即检测概率)以使得自己的效用最大化；另一方面，平台获得检测数据需要付出支付给用户费用，并且支付的费用与数据的检测概率成正比，因此N个用户和平台为了得到自身效用的最优进行博弈，构成了一个N+1的非合作微分博弈。令v(t)表示在时刻t(t∈[t0,T])平台发布的频谱感知任务单价，ui(t)表示次用户i在时刻t提供的对频谱的检测概率，x(t)表示所有次用户从开始到时刻t(t∈[t0,T])上报的所有的感知数据量。x(t)会随着用户上报的检测概率和平台决定的任务价值而改变，其变化可以用微分方程表示为：

(3)

其中，a，b，c为归一化因子，a>0，b>0表示次用户上报检测概率对最终的数据量的影响，c>0表示平台对任务定价对数据量的影响。

每个用户根据检测概率的大小获得收益，用户的收益和检测概率成正比，定义收益函数：

gi=ui(t)v(t)

(4)

用户进行频谱感知需要消耗存储资源和电量，将数据上传至平台时需要消耗电量，因此定义其代价函数：

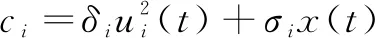
(5)

其中，δi表示次用户i频谱感知的代价，δi与信噪比成反比，次用户的信噪比越大，δi越小。σi表示次用户i上传数据的代价，σi与用户到基站的距离成有关，因此可以定义次用户i的效用函数：

(6)

其中，α>0为加权因子。

次用户的目标是最大化个人的累计效用，表示为：

σix(t)]e-r(t-t0)dt+qix(T)e-r(T-t0)

(7)

其中，r>0表示折扣因子，T-t0表示博弈时长，qix(T)表示次用户的边缘效用[15]。

平台完成任务会获得第三方的报酬，定义收益函数为：

(8)

平台需要付给次用户报酬以及处理接收到的数据，因此定义平台的代价函数为：

(9)

其中，m>0表示平台处理数据的花费。因此定义平台的效用函数为：

(10)

其中，β>0为加权因子。

平台的目标是最大化累计效用，故表示为：

(11)

其中，r>0表示折扣因子，T-t0表示博弈时间间隔，qx(T)表示平台的边缘效用。

2 反馈纳什均衡求解

根据建立的非合作微分博弈模型(3)、(7)、(11)，求解该模型的反馈纳什均衡。每个次用户通过优化上报结果的检测概率以使效用最大化，平台通过优化任务的价格以获得自身效用的最优，下面将推导次用户的最优检测概率和平台最优价格的表达式。

(12)

Ui(T,x)=qix(T)e-r(T-t0)

(13)

对式(12)求ui(t)的一阶导，并令其等于0，得到反馈纳什均衡的解：

(14)

对于平台来说，如果存在连续微分函数V(t,x):[t0,T]×R→R满足以下的偏微分方程，则策略集v*(t)=φ*(t)是(3)和(11)的反馈纳什均衡解[15]：

mx(t)]e-r(t-t0)+Vx(t,x)[ax(t)+

(15)

V(T,x)=qx(T)e-r(T-t0)

(16)

对式(15)求v(t)的一阶导，并令其等于0，得到反馈纳什均衡的解：

(17)

引理1：博弈模型(12)-(13)、(15)-(16)的纳什均衡解可以表示为[16]：

Ui(t,x)=e-r(t-t0)[Ai(t)x+Bi(t)]

(18)

V(t,x)=e-r(t-t0)[A(t)x+B(t)]

(19)

其中,

(20)

Ai(T)=qi

(21)

(22)

A(T)=q

(23)

证明：将式(18)和式(19)分别对x和t求导，得到如下的表达式：

(24)

(25)

Vx(t,x)=e-r(t-t0)A(t)

(26)

Vt(t,x)=

(27)

将式(24)-(25)带入式(12)-(13)：

e-r(T-t0)[Ai(T)x+Bi(T)]=e-r(T-t0)qix(T)

(29)

为了使得式(28)-(29)成立，应满足下面的条件：

(30)

求解微分方程(30)，得到下面的表达式：

(31)

将式(26)-(27)带入式(12)-(13)：

e-r(T-t0)[A(T)x+B(T)]=e-r(T-t0)qx(T)

(33)

为了使得式(32)-(33)成立，应满足下面的条件：

(34)

求解微分方程(34)，得到下面的表达式：

(35)

根据式(14)、(17)、(24)、(26)、(31)、(35)，可以得到用户检测概率和平台定价的最优解分别为：

(36)

(37)

(39)

将式(37)-(38)代入微分方程(3)，可以得到非合作微分博弈最优状态表达式：

(40)

3 仿真结果与分析

该文采用MATLAB进行仿真，假设参与感知的次用户数为3，T=5，折扣因子r=0.05，δi服从期望为0.5，方差为0.05的正态分布，σi服从期望为0.26，方差为0.05的正态分布，qi服从期望为1.8，方差为0.05的正态分布，采样频率为10 MHz，次用户的虚警概率为0.01，其余参数如表1所示。

表1 参数设置

图2(a)给出了r=0.05时三个次用户的最优策略随时间变化曲线。从图中可以看出次用户最优的检测概率随着时间的增加而增大，这是因为次用户提高检测概率参与频谱感知可以获得更多的报酬，为了使得效用最大，次用户会更愿意参与感知任务。

图2(b)给出了r=0.05时用户的最优感知时间变化曲线。用户的信噪比与发射功率和到主用户的距离相关，从仿真图可以看到用户的感知时间逐渐上升，这是因为在确定的信噪比条件下，检测概率确定后可由式(1)计算感知时间。

(a)r=0.05时次用户最优检测概率ui/t随时间变化曲线

(b)r=0.05时次用户最优感知时间变化曲线图2 仿真曲线

图3给出了r=0.05时平台最优价格v(t)随时间变化曲线。从仿真图可以看到任务的价格随着时间的增加而减小，这是因为随着时间的增加，平台能收到的信息增多，平台为了提高自身效用则尽可能地降低价格。

图4给出了r取不同值时平台效用随时间变化曲线。从仿真图可以看到r越大平台的效用越高。当r不变时，平台的效用随着时间的增加而减小，这是因为v(t)随着时间的增加而减小，平台得到的收益也会随之下降。

图3 r=0.05时平台最优价格v/t随时间变化曲线

图4 平台效用随时间变化曲线

图5给出了当用户均采用最优检测概率时，平台分别取最优价格和固定价格时效用随用户数变化曲线。固定价格取值为0.385，从仿真图可以看到平台采用最优价格时，平台效用值高于取固定价格相对应的效用，对平台来说，招募到更多的用户数可以提高检测概率，第三方支付的报酬会增加，平台效用增加，因此取最优价格能够提高平台的效用。

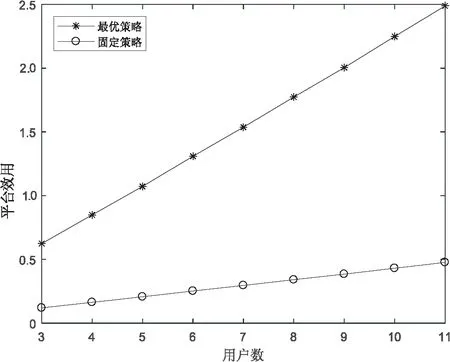
图5 平台取最优价格与固定价格时效用 随用户数变化曲线

图6给出了当平台取最优价格时，用户分别取最优检测概率和固定检测概率时的平均效用变化曲线。检测概率均取0.6，从仿真图可以看到用户采取最优检测概率时，用户的平均效用高于取固定价格相对应的平均效用，因此取最优检测概率能够提高用户的平均效用。对用户来说，当采取最优检测概率时，用户的平均效用高于取固定价格相对应的平均效用，随着用户数增加，平台所能增加的检测概率相对减小，用户的平均效用随之下降；当用户采取固定策略时，用户的平均效用随着用户数的增加而增加，这是因为随着用户数增加，第三方给的报酬会增加，所以用户的平均效用会增加。

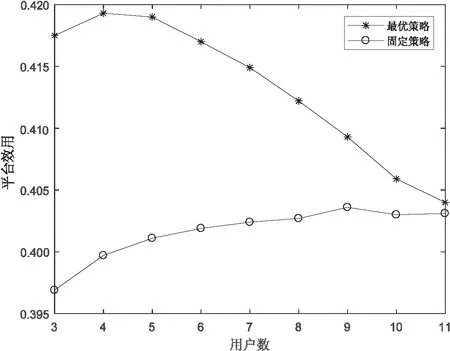
图6 用户取最优检测概率与固定检测概率时 平均效用随用户数变化曲线

4 结束语

通信技术的开展离不开计算机技术，当下用户对通信技术最关注的是其可靠性、安全性和保密性，将计算机技术的优势和功能与通信技术结合起来，可以加快计算机通信技术的发展。该文将群智感知与频谱感知相结合，提出了一种基于微分博弈的群智频谱感知算法。平台的效用定义为第三方支付的报酬减去付给次用户的报酬，次用户的效用定义为平台支付的报酬减去次用户参与频谱感知任务的成本，以各自效用最大为目标设计了一种非合作的微分博弈模型，通过求解反馈纳什均衡获得了平台和用户的最优策略，即平台决定任务的最优价格，各个次用户确定频谱的最优检测概率(即感知时间)。仿真结果表明，平台和次用户采取最优策略时效用高于采取固定策略时的效用。