基于正则化KL距离的交叉验证折数K的选择

褚荣燕，王 钰，杨杏丽，李济洪

(1.山西大学 数学科学学院，山西 太原 030006；2.山西大学 现代教育技术学院，山西 太原 030006；3.山西大学 软件学院，山西 太原 030006)

0 引 言

在机器学习中，交叉验证技术广泛地应用于模型(算法)性能评估、特征选择、模型选择、模型参数确定、过拟合检验等任务[1-5]。例如，给定一组线性空间(模型)，在这些线性空间(模型)中选择最佳的最小二乘估计量时可用交叉验证进行模型选择。所谓交叉验证技术，即数据集被随机地切分为多个训练集和测试集，训练集用来进行模型的拟合，测试集用来进行模型性能的评估，最后通过多次性能评估的均值(投票)来分析模型的优劣。其中，常见的交叉验证技术包括留一(leave-one-out)交叉验证、Hold-out交叉验证、RLT(repeated learning testing)交叉验证、5×2交叉验证、组块3×2交叉验证、组块m×2交叉验证、K折交叉验证等[6-9]。在这些交叉验证技术中，K折交叉验证是最广泛使用的方法，因为它依赖于一个整数参数K，比其他经典交叉验证方法的计算代价更小。K折交叉验证指的是数据集被平均分成K个大小近似相同但不相交的子集，选取其中K-1个子集作为训练集来拟合模型，剩下的一个子集作为测试集来评估模型性能。然而，在机器学习中，关于K折交叉验证方法的折数K的选择虽然很多文献中都对其进行了研究并给出了推荐，但它一直是一个公开未解决的问题[10-15]。比如文献[6]中提到当模型选择的目标是估计时，最优的折数K为5到10之间，这是因为K值越大，统计性能不会增加太多，并且小于10次分割的平均值在计算上仍然可行。文献[8，11，12，14]皆推荐在进行泛化误差估计，算法性能对照和超参数选择时应选择二折或多次二折重复的交叉验证(5×2交叉验证、组块3×2交叉验证、组块m×2交叉验证)。文献[15]在多个分类器下的大量实验中验证了在进行模型精度估计和模型选择时十折交叉验证优于留一交叉验证。另外，注意到上述文献中大多是从模型性能评估和选择的角度来进行折数的选择，但事实上，执行上述交叉验证过程的一个前提条件是训练样本和测试样本的分布一致，然而在实际中对于训练样本和测试样本的分布是否一致许多文献中并没有验证。因此，该文考虑通过度量训练样本和测试样本的分布一致性来进行K折交叉验证折数K的选择。

实际中，常用的度量两个分布函数之间差异的度量有KL(Kullback-Leibler)距离、全变差(total variation)距离、海灵格(Hellinger)距离、KMM(kernel mean matching)度量、MMD(maximum mean discrepancy)度量、Wasserstein 距离等[16-17]，其中KL距离是最简单且广泛使用的方法。因此，该文基于KL距离进行K折交叉验证中折数K的选择。

为此在UCI数据库中选取的四个数据集上进行了实验，实验发现直接用KL距离来进行K折交叉验证中折数K的选择可能是不合理的，因为如图1所示，随着K折交叉验证折数K的增加，训练样本和测试样本分布间KL距离也在增大，这样直接基于KL距离进行折数K的选择往往选出的都是最小的或接近最小的折数K。因此不能直接应用KL距离来进行K折交叉验证折数K的选择，为此考虑通过对KL距离增加一个随着折数K增加而变小的正则化项来得到一个正则化的KL距离，以此作为交叉验证中折数K的选择准则。

图1 随着折数K的变化KL距离的变化

1 KL距离

在两个分布函数之间差异的度量中最广泛使用的方法是KL距离。接下来给出KL距离的定义。

如果记P(x)和Q(x)是两个已知的分布函数，则P(x)和Q(x)之间的KL距离为：

(1)

特别地，当P(x)和Q(x)分别为高斯分布Nd(uS,ΣS)和Nd(uF,ΣF)时，根据矩阵的性质及多元高斯分布期望和协方差的性质[18]，其KL距离可写为:

(2)

具体地，在对数据进行分析时，P(x)和Q(x)的总体均值和总体协方差一般使用样本均值和样本协方差来估计[19]：

(3)

(4)

此时，把式(3)和式(4)代入式(2)中，得到式(5)：

(5)

2 K折交叉验证折数K的选择准则

本节我们将基于上一节定义的KL距离进行具体分析，通过对原始KL距离增加一正则化项，利用此正则化KL距离来选择使得训练样本和测试样本分布尽可能一致的K折交叉验证的折数K。

2.1 K折交叉验证折数K的选择准则

观察式(5)发现DKL[P(x)||Q(x)]≠DKL[Q(x)||P(x)]，也就是说KL距离不是对称的，因此该文考虑对称的KL距离，即：

(6)

进一步，基于K折交叉验证K次重复的对称KL距离为：

(7)

虽然，在经验上，基于训练样本与测试样本的KL距离选择合适的折数K的方法是一个比较理想的方法，但是在实际结果中发现直接基于式(7)进行K折交叉验证折数K的选择并不是一个好的方法(详见图1)，因为随着折数K的增加KL距离也会增大，这会导致几乎所有数据选出的折数都较小。为了解决此问题，该文进一步提出了一种新的基于正则化KL距离的K折交叉验证折数K的选择准则。

2.2 正则化KL距离的K折交叉验证折数K的选择

把一个随着折数K增加而减小的函数作为一个正则化项添加到式(7)中，这样对原始KL距离起到折中作用。为此，给出如下正则化KL距离选择准则:

DReKL(K)=DAKL[P(x),Q(x)]+λf(K)

(8)

其中，DAKL[·]定义为第K折训练样本与测试样本之间的平均KL距离，K为折数；f(K)是关于K的函数；λ是调节参数，通过调整λ确定正则化的程度。这时，基于最小化正则化KL距离的交叉验证折数K的选择准则为：

(9)

3 真实数据实验

选取了UCI数据库中的Wholesale customers，Wine，wine quality-red，wine quality-white四个数据集来进行实验，以验证提出的基于正则化KL距离的K折交叉验证折数K的选择准则的合理性和有效性。

3.1 实验设置

四个数据集的相关描述如下：

(1)Wholesale customers数据集：关于批发商批发产品年度支出的一个二类分类(三类分类)数据集，根据批发商渠道把其中的餐饮业渠道分为第一类，零售渠道分为第二类(或按照客户所在的区域(里斯本，波尔图，其他区域这三个区域)把数据分为三类)，包含7个特征(Fresh，Milk，Grocery，Frozen等特征)，共440个样本。

(2)Wine数据集：关于三种不同品种的葡萄酒化学分析的一个三类分类数据集，三种葡萄酒即为三类，含有13个特征(Malic acid，Ash，Alkalinity of ash，Magnesium等特征)且每个特征是连续的变量，共178个样本。

(3)wine quality-red数据集：关于红葡萄酒质量优劣检测的一个二类分类(六类分类)数据集，根据酒的质量把质量指标大于5的分成一类，质量指标小于等于5的分成另一类(或不同的指标各表示一类)，包含11个特征(fixed acidity，volatile acidity，citric acid，residual sugar等特征)，共1 599个样本。

(4)wine quality-white数据集：关于白葡萄酒质量优劣检测的一个二类分类(七类分类)数据集，根据酒的质量把质量指标大于5的分成一类，质量指标小于等于5的分成另一类(或不同的指标各表示一类)，包含11个特征(fixed acidity，volatile acidity，citric acid，residual sugar等特征)，共4 898个样本。

此外为了考虑不同类别对于KL距离的影响，按照数据的属性描述重新进行了分类。例如Wholesale customers数据根据渠道和区域分为3类和2类，wine quality-red数据根据质量指标分为6类和2类，wine quality-white数据根据质量指标分为7类和2类。

在式(8)给出的基于正则化KL距离的选择准则中，正则化函数设置为f(K)=exp(-K)。这是因为在如Wholesale customers数据集中，KL距离是从2.12×1014变化到6.71×1016，而折数K是从2变化到220，它们是不同数量级的，因此，为了二者的折中，不失一般性，正则化函数设置为f(K)=exp(-K)。事实上，不同的正则化函数(例如log(x)函数，exp(x)函数)对于最优折数K的选择是没有影响的。因为对于不同的正则化函数，通过调节不同的调节参数值始终可以选出相同的最优折数K，只是收敛速度不同罢了[20]。

进一步，为了保证实验的准确性，对该实验过程重复1 000次，最后取这1 000次的平均值作为最终正则化KL距离。

注：交叉验证折数K的实际取值范围为[2，n/2]，n为数据容量，因为在使用多元高斯分布来估计KL距离时，训练集/测试集最小需要两个样本估计样本协方差阵。

3.2 实验结果

基于3.1节的数据集，首先验证了随着K折交叉验证的折数K的增加，所有训练样本和测试样本分布之间的KL距离逐渐增大。然后，给出了基于提出的正则化KL距离的K折交叉验证折数K的选择准则的选择结果。

图1展示了不同折交叉验证的训练样本和测试样本之间的KL距离。根据图1，首先可以看到所有训练样本和测试样本分布之间的差异是明显的，例如，在Wholesale customers数据中，折数从2折增到10折时，对应的KL距离从2.12×1014上升到7.04×1014，在Wine数据中，折数从2折增到10折时，对应的KL距离从3.31×107上升到9.94×107。第二，图中直观地显示了随着折数K的增加，KL距离逐渐增大。例如，wine quality-red数据集中，折数范围从2变化到799时，KL距离从1 532上升到6.05×105。wine quality-white数据集中，折数范围从2变化到2 449时，KL距离从1 695上升到1.26×106，也就是说当折数从2上升到n/2(n为样本量)时，不同数据的KL距离都是持续上升的。且几乎所有数据训练样本和测试样本的KL距离都是2折或者接近2折时最小，显然这是不合适的，因为它总选择最小或接近最小的折数，因此为KL距离增加一个正则化项，提出了基于正则化KL距离的K折交叉验证折数K的选择准则，通过最小化式(8)中给出的准则来选择最优折数。结果如图2所示。

(a) (b)

图2展示了正则化后的DReKL(·)变化趋势。为了更清楚地看到正则化KL距离的变化，表1～表4给出了K=2，5，8，9，10，11，12，13，14，15，20时，四个数据集上正则化KL距离的数值。首先可以看出，随着折数的增加正则化KL距离先减小后增大，例如在表1的Wholesale customers数据集中3类的情况下，9折时正则化KL距离的值为7.27×1014，10折时正则化KL距离的值为7.18×1014，20折时正则化KL距离的值为15.92×1014。在表2的Wine数据集中，9折时正则化KL距离的值为10×107，10折时正则化KL距离的值为9.94×107，20折时正则化KL距离的值为19.47×107。在表4的wine quality-white数据集中，9折时正则化KL距离的值为9.93×103，10折时正则化KL距离的值为6.23×103，20折时正则化KL距离的值为7.78×103，这都验证了提出的方法是合适的。

表1 Wholesale customers数据集的DCKL距离结果

表2 Wine数据集的DCKL距离结果

另外，可以在表1～表4中看到每个数据的最优折数(表1～表4中的黑色粗斜体表示不同数据分为2类时最优的折数及其对应的正则化KL距离值，黑色粗体表示不同数据分为其他类时最优的折数及其对应的正则化KL距离值)，例如Wholesale-customers数据分3类时最优折数为10折，分2类时最优折数为9折。Wine数据最优折数为10折。wine quality-red数据分6类时最优折数10折，2类时最优折数为9折。wine quality-white数据分为7类时最优折数为12折，2类时最优折数为12折。最后，发现不同分类类别对同一数据集的训练样本和测试样本之间的正则化KL距离是有影响的，一般情况下同一数据集下多类分类比二类分类的正则化KL距离的差异小(除Wholesale customers数据集外)，例如在表4中，当折数为12时，7类的正则化KL距离的数值约为5.17×103，2类的正则化KL距离的数值约为5.25×103。

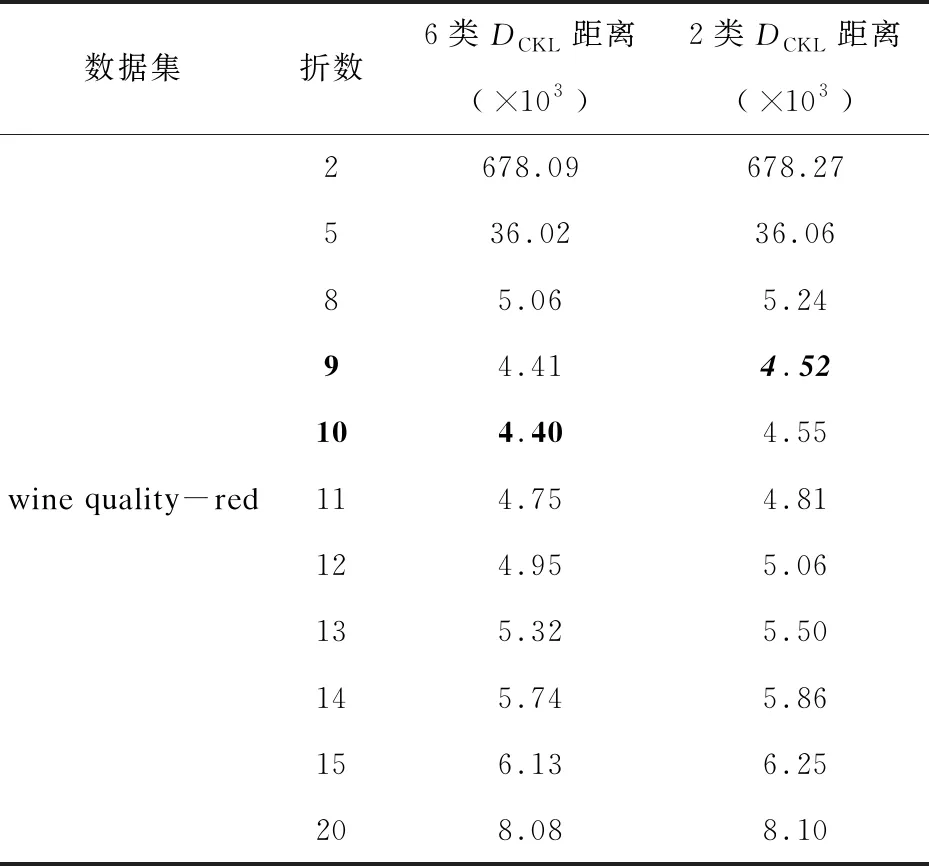
表3 wine quality-red数据集的DCKL距离结果

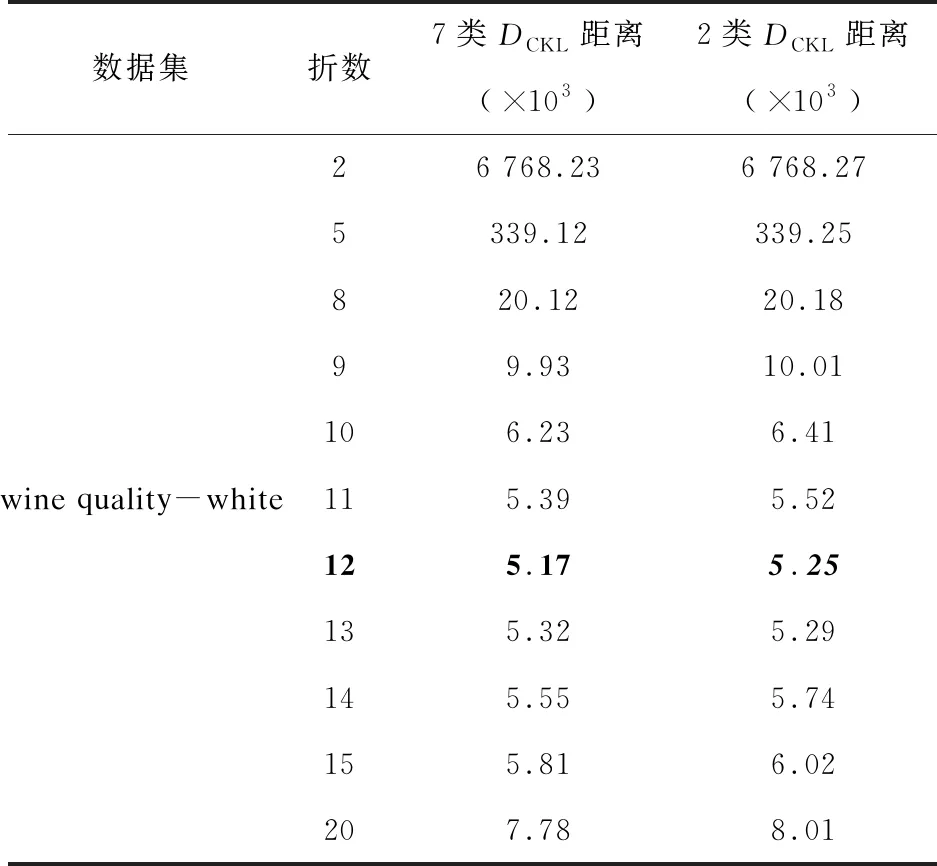
表4 wine quality-white数据集的DCKL距离结果

4 结束语

K折交叉验证技术在机器学习和统计学中被广泛使用，但关于其折数K的选择一直是一个公开未解决的问题。而在传统的机器学习中使用K折交叉验证进行分析时，都是在假设训练样本和测试样本分布一致进行的，但是实际中训练样本和测试样本的分布往往不一致。该文在考虑K折交叉验证过程中训练样本和测试样本的分布一致性的情况下，利用KL距离来度量训练集样本和测试集样本二者分布的差异，通过实验发现直接使用KL距离进行选择时，往往选出的是最小的或者接近最小的折数，这并不合理。基于此，提出了一种基于正则化KL距离的K折交叉验证折数K的选择准则。并通过UCI数据库中的四个数据集对提出的准则进行验证，最终结果验证了该选择准则的合理性和有效性。

同时我们应该看到，虽然我们通过使训练样本和测试样本的分布差异最小化选出了K折交叉验证的合适的折数K，但是训练样本和测试样本的分布之间仍存在差异，本文并未给出使训练集与测试集尽可能一致的校正策略，未来我们将在此框架下进一步研究二者分布的校正策略。