网络Meta分析研究进展系列（八）：多重关联结局的多元网络Meta分析

杨智荣，武珊珊，董圣杰，张天嵩，田金徽，孙凤

作为传统Meta分析的拓展，网络Meta分析（Network Meta-analysis，NMA）可同时比较多种干预措施的效果，并可对所有干预措施的效果进行排序。然而，每个NMA通常只针对某一结局，例如分别对收缩压和舒张压进行合并，而忽视了结局间的关联性（如高血压患者的收缩压与舒张压的关联）。这种个体水平上的关联性会导致群体（研究）水平效应间的关联。这类具有高度相关性的结局统称为多重关联结局[1]。除上述血压的例子外，这类结局在其他情况下也很常见，如同一结局的多个时间点测量、多个生物标记物（如不同的血脂成分）、对同一结局的混杂因素进行部分调整（如只调整年龄、性别）和完全调整（如同时调整年龄、性别、生活方式、合并症等）的效应估计量，多个测量准确性的指标（如灵敏度和特异度），以及对同一结局不同的测量方式（如测量疼痛程度的不同评分工具）[1]。若对关联性结局逐个合并，除忽略了相关性以外，每次合并单个结局时那些没有报告该结局的研究也会被排除，可能会造成有偏估计，且降低估计的精确度。

多重关联结局的多元NMA分析可帮助解决上述问题。它一方面可把所有具有关联性的结局同时纳入同一个模型里进行合并，在估计效应值时考虑了不同结局间的相关性，另一方面可以把报告了任意一个关联性结局的研究都纳入Meta分析，从而增加样本量和结局信息，可一定程度上减少结局选择性报告偏倚的影响[1]。

以一篇关于家庭安全教育和安全防护用具对预防儿童伤害的效果的Cochrane系统综述为例[2]，该综述比较了九项不同的干预措施，涉及三个具有相关性的结局，包括药物的安全存放、其他家庭用品的安全存放、存有毒品控制中心的电话号码，报告了任一结局的随机对照试验共有22个。这三个关联结局理论上可有七种不同组合的报告情形（表1）。若对每个结局分别进行NMA，则纳入分析的研究数目分别只有13个（情形1、4、5、7）、15个（情形2、4、6、7）和10个（情形3、5、6、7），而且忽略了各结局之间的相关性。若采用多元NMA同时分析这三个结局，则可把22个研究都纳入模型，而且可在模型中明确定义结局之间的相关性。

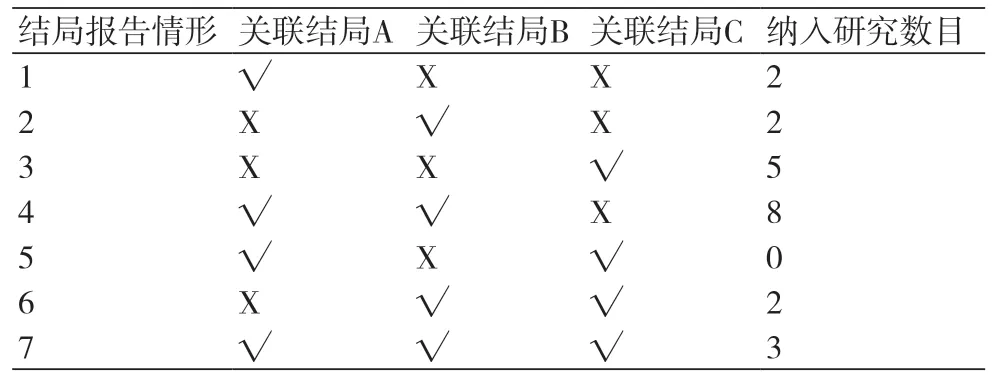
表1 三个关联结局在证据网络中的报告情况

1 三类模型

多重关联结局的多元NMA是在经典单元NMA（每次只分析一个结局）的基础上拓展而来的。以下先简要回顾基于干预组数据（arm-based）二分类结局的经典NMA的贝叶斯模型，然后介绍由Achana等于2014年提出的多元NMA，包括基础模型和全模型[3]。该模型在随后的方法学研究中得到多次引用和完善。

1.1 基于干预组数据的经典网络Meta分析（单元模型）设NMA证据网络中一共纳入N个研究（i=1,2,…,N），K种干预措施，rik表示在第i个研究中第k个干预组所观察到的结局发生例数，nik表示第i个研究中第k个干预组所纳入的样本量，则NMA随机效应模型如下：

若对多重关联结局采用经典NMA来分析，那么每次只能分析其中一个结局，忽略结局之间的相关性，那些没有报告该结局（尽管可能有报告其他与之相关的结局）的研究就会被排除。

1.2 基于干预组数据的多重关联结局的多元网络Meta分析的基础模型在经典网络NMA的基础上，多元网络NMA利用多元正态分布把结局之间的相关性也考虑在模型里。设NMA证据网络中共纳入N（i=1,2,……N）个研究，k（k=A,B,C,……）种干预措施，m（m=1,2,…,M）个具有相关性结局，rikm表示在第i个研究中第k个干预组所观察到的第m个结局发生例数，nik表示第i个研究中第k个干预组所纳入的样本量，则多元NMA随机效应模型如下[3]：

若对多重关联结局采用多元NMA来分析，那么可以同时把所有结局纳入模型来分析，模型考虑结局之间的相关性，只要报告了其中任一结局的研究都会纳入模型。对于那些没有报告所有多重关联结局的研究，未报告的结局信息会被视作随机缺失。

如果有比较对在整个证据网络中完全没有涉及某一结局，那么这些比较对在该结局上相对效应就不会在模型中得到估计。为解决这一问题，可进一步假设所有干预措施与共同对照的相对效应在所有相关结局上都是相似的（恒定效力假设），此时就可以估计所有相对效应的基本参数（见下述）。

1.3 基于干预组数据的多重关联结局的多元网络Meta分析的全模型为得到所有基本参数的估计值，可对上述基础模型进行拓展，即对所有基本参数d(Ak)m的分布进行设定[3]。当存在K种干预措施（k=1表示共同对照）、M个多重关联结局时，假设所有基本参数d(Ak)m服从正态分布：

2 实例分析及WinBUGS代码

以前面提及的Cochrane系统综述中的数据为例[2]，使用WinBUGS软件拟合上述三种模型。在NMA证据网络中涉及22个研究（表2），包含常规措施（UC）、教育（E）、教育+免费设备（E+FE）、教育+免费设备+家庭安全检查（E+FE+HSI）、教育+免费设备+附加设备（E+FE+F）、教育+家庭安全检查（E+HSI）、教育+免费设备+家庭安全检查+附加设备（E+FE+HSI+F）、教育+家访（E+HV）、免费设备（FE）等九项干预措施。多重关联性结局包括三个，即药物的安全存放（A）、其他家庭用品的安全存放（B）、存有毒品控制中心的电话号码（C）。模型可通过Achana等在其文章中提供的WinBUGS代码实现[3]。

模型拟合的第一步：计算22个纳入研究各干预组各结局的效应比值的对数及其标准误。计算结果如表2所示，表2也是在WinBUGS中运行模型时所需要的数据格式。

模型拟合的第三步：分别拟合单元模型、多元基础模型和多元全模型。在多元NMA全模型中一共有24个基本参数，但由于整个证据网络中没有涉及E+FE+F与UC在结局C的比较、E+HSI与UC在结局A和B的比较、E+HV与UC在结局A和B的比较、FE与UC在结局C的比较，因此在单元NMA模型和多元NMA基础模型只有18个效应值的基本参数。对多元基础模型，分别对∑(M×M)的先验分布整体设置为Inverse-Wishart分布或分开参数设置为均匀分布。图4展示了各种干预措施与常规措施（UC）在三个关联结局上比较的效应值。

3 讨论

从实例三类模型（表4）中可以看出，多元NMA的基础模型和传统的单元NMA模型相比，效应估计值的精确度并没有明显提高，而全模型基于不同结局的效应值相似的假设（恒定效力假设），利用了其他关联结局的信息，因而一定程度上提高了效应估计值的精确度（可信区间更窄），某些效应值的估计结果可能与基础模型的不同（如表4中干预FE的结局B）。目前多元NMA多在贝叶斯框架下，通过软件WinBUGS或OpenBUGS实现。表5总结了三类模型的特点。

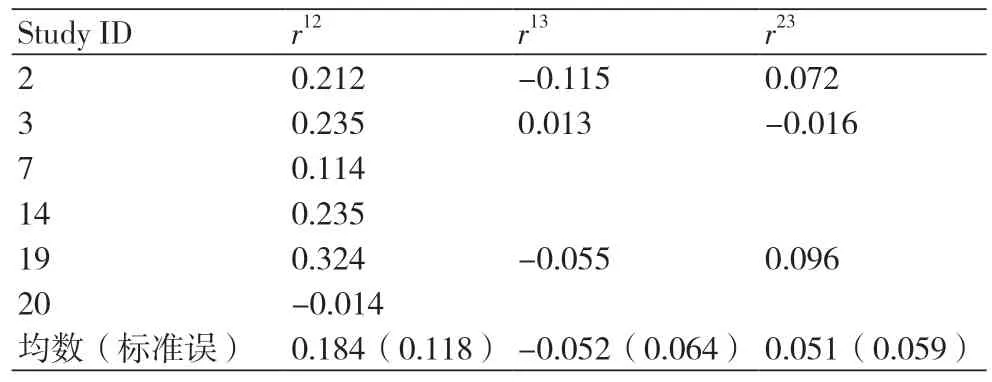
表3 基于个体资料计算Pearson相关系数

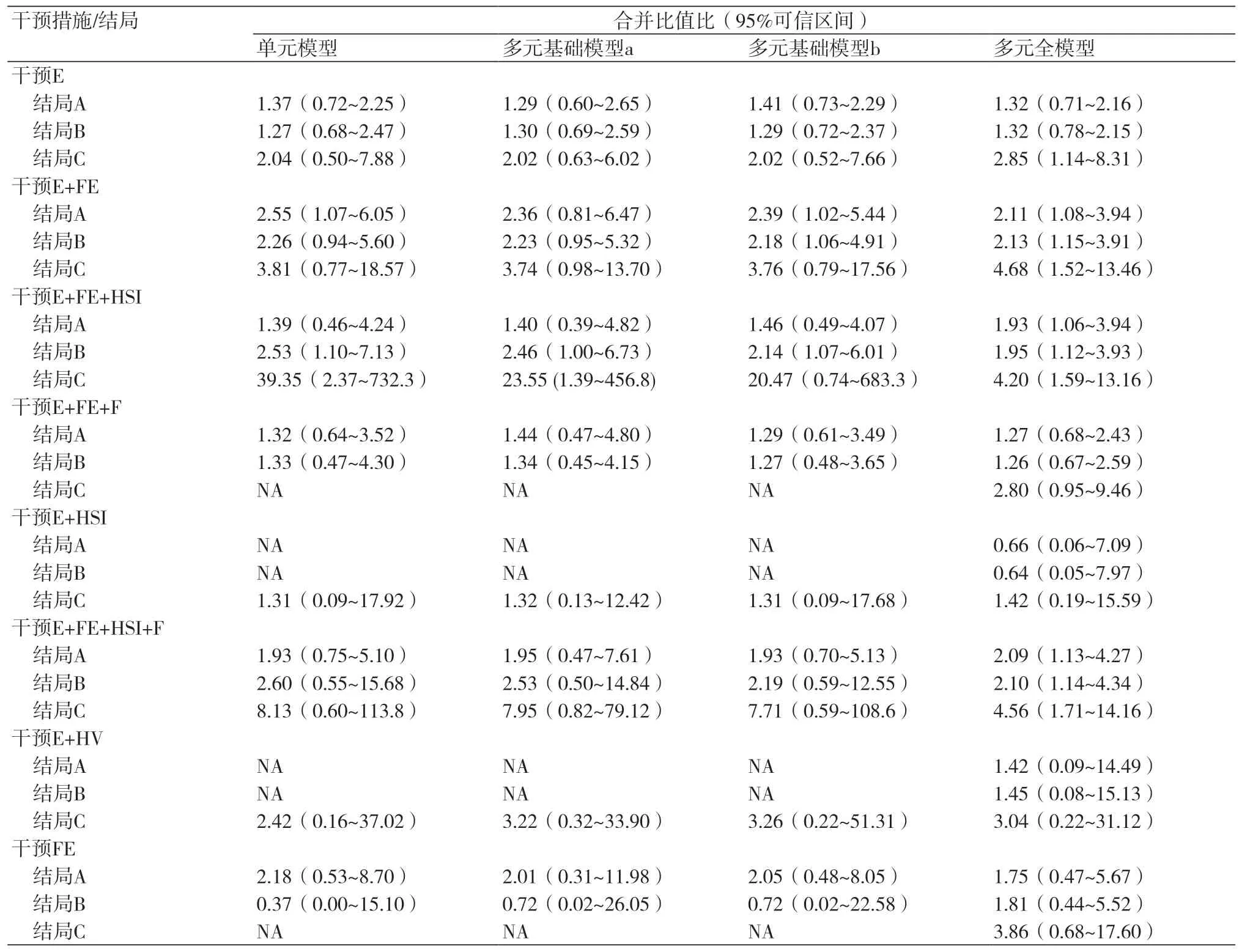
表4 各种干预措施与常规措施在三个关联结局上比较的效应值

除了本文介绍的实例，多重关联结局的多元NMA还尝试在复发缓解型多发性硬化症的治疗[4]、急性脑卒中的治疗[5]、抑郁症的治疗[6]等领域应用。但这些实例主要是用于方法学的探讨，真正应用多元NMA来合并多重关联结局的研究目前还很有限。

采用多元NMA模型有以下注意事项：

（1）模型的适用范围：多元NMA不仅适用于相关但不同的多个结局，也适用于同一个结局不同时间点的测量，尤其适用于某一结局的直接证据很少，但其他相关结局的证据较多，而且这些结局之间的相关性较高的情况。虽然本文所介绍的模型针对的是二分类结局，但对连续性结局也可以使用多元NMA。在这种情况下，借用强度（Borrowing of Strength，BoS，是指因关联证据的纳入而使得某个汇总结果方差减少的百分比）会增加[1]。当结局之间不相关或相关性较低时，使用多元NMA所带来的BoS较小，对精确度的提高有限，同时还会增加要估计的参数。

（2）对前提假设的考虑：多元NMA在单元NMA的三个假设的基础上，还要求所有比较对在同一结局上的研究间方差相等，在不同结局上的研究间协方差相等。这个设定可以简化协方差结构，减少模型的参数，但这是一个很强的假定，在实际应用多元NMA时需要考虑这个设定的合理性。在此基础之上，多元NMA的全模型还增加了恒定效力假设，即要求任一比较对在不同结局上的效应值来自同一个正态总体。如果结局的定义和测量相似（如上述实例），那么这个假设是合理的[3]。若这一假设不满足，使用全模型可能会导致有偏估计。

（3）纳入研究数目较少：即使可如上述通过简化方差协方差结构来减少模型参数，但有时候还是不能满足检验效能。依据经验法则，多元NMA所需的研究数目为3×(p+∑pi=1i)，其中p为关联结局的总数[5]。按照这个公式，当用多元NMA分析两个、三个或四个关联性结局的时候，相应的所需要的研究数目应至少有15、27和42个。

（4）研究内相关系数的确定：该系数在本文所介绍的多元NMA中是假设已知的，它的确定是进行多元NMA的重要一步，其确定可基于个体资料数据（如实例），外部证据[5]，研究报告中汇总数据[7]，专家意见[8]，模糊先验分布[9]，或对相关系数进行假设并作敏感性分析[4]。

（5）本文所介绍的多元NMA是通过假设观察到的比值对数服从正态分布来近似二项分布，该假设适用于多重关联结局为二分类结局且发生频率总和不为1的情况[10]。然而，当结局发生数较少时，这种近似处理不一定合适，而需要用到个体资料数据[3]。基于汇总数据的方法还在进一步研究中。

（6）本文所介绍的多元NMA均是一致性模型，若一致性假设不成立时，需要采用不一致模型，但目前尚无比较公认的不一致模型[3]。

多元NMA模型是当前NMA方法学的研究和应用里相对还不太成熟的一个领域。近年来多元NMA的方法学在减少结局选择性偏倚[6]、研究内相关系数的确定[5,11]、BoS的估算[12]、权重的计算[12]等领域开始有进一步的发展。相比单元NMA，多元NMA所需要的纳入研究数目更多，在确定研究内相关系数这一关键步骤上有一定难度，加之方法学有待完善，因此可能限制了它的应用。当前关于多元NMA的文章，大部分是方法学研究，但随着方法学的不断发展，相信多元NMA的实际应用会得到进一步推广。

表5 三类模型的特点