APU转子振动特性分析

乔思佳，刘成峰

(航空机电系统综合航空科技重点实验室 航空工业南京机电液压工程研究中心，江苏 南京 211106)

0 引言

辅助动力装置(APU)是安装在飞机上的一套不依靠机外任何能源、自成体系的小型动力装置，其主要作用是向飞机的主发动机以及环控系统提供压缩空气，还可以为飞机提供电力保障[1]。

APU作为一种小型的燃气涡轮发动机，由单级离心压气机、环形回流燃烧室、单级向心涡轮组成其动力部分，压气机和涡轮固定在同一个轴上，该轴的另一端驱动附件齿轮箱。

由于APU转子的设计额定转速较高，达45 225 r/min，转子在结构设计时需要使临界转速远离额定转速，从而防止发生共振而产生破坏。本文基于某型APU的设计结构，利用Hypermesh与Workbench软件对转子的固有模态及临界转速进行计算分析，从而校核该转子设计的合理性。

1 转子动力学计算方法

一般来说，一个机械系统的动力学微分方程可表示为：

(1)

其中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；F为激振力列阵；x为位移列阵。

式(1)为一般机械系统的有阻尼振动微分方程，通过求解微分方程的特征值和特征向量，可以得到系统的固有频率及振型[2]。

转子动力学与结构动力学不同的是转子在旋转状态会产生陀螺效应，陀螺效应会改变转子的刚度，使得转子的固有频率在各转速下发生变化。

考虑流体动力轴承的油膜力和轴承油膜产生的集中阻尼，转子系统的运动微分方程式可写成：

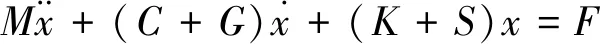
(2)

其中：G为陀螺矩阵；S为刚度矩阵的不对称部分[3]。

目前，关于转子系统振动特性的分析方法主要有解析法、有限元法、传递矩阵法等。有限元法和传递矩阵法主要用于复杂的多转子或多轴承系统，而有限元法与传递矩阵法相比能够充分模拟转子的振动特性，且具有较好的计算精度[4]，因此本文利用有限元法对转子特性进行计算。

2 APU转子有限元建模

本文利用有限元软件对某型APU进行动力学计算。对APU进行动力学分析时进行较少的模型简化，与实际模型尽量保持一致，以提高计算精确度。

2.1 转子结构

APU转子主要由涡轮、压气机、中心拉杆、转子轴垫、音轮、自锁螺母和迷宫密封等部件组成，涡轮与压气机轴之间靠圆弧端齿定心定位和传递扭矩，并通过中心拉杆和锁紧螺母压紧在一起，转子系统由两个滚动轴承支承，分别位于转子轴垫的两端。APU转子结构如图1所示。

图1 APU转子结构

由于转子模态主要与质量和刚度有关，去除转子模型中的小尺寸倒角及油孔，不影响转子动力学特性的计算，且会减少有限元网格数量。

涡轮与压气机的叶片形状不规则，极大地增加了前处理难度，将涡轮、压气机的叶片切除，简化成集中质量。叶片简化模型特征参数见表1。其中，Ix、Iy、Iz分别为叶片绕x、y及z轴的转动惯量。由于转子绕x轴旋转，因此Iy=Iz。简化后的转子模型如图2所示。

表1 叶片简化模型特征参数

图2 简化后转子模型

辅助动力装置转子是一个装配体，包括多个材料特性。Ansys中材料属性可以定义为各向同性或者各向异性，且可以为同一模型的不同区域分别制定不同的材料，为建模提供了极大的方便。假设转子的材料在弹性工作范围之内，因此实体单元的材料属性需要定义弹性模量、泊松比及材料密度。辅助动力装置转子各部件材料参数见表2。

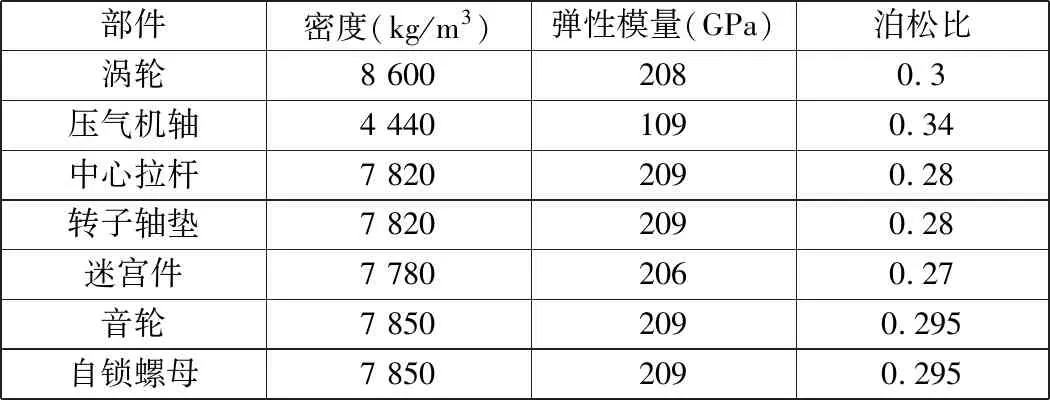
表2 某型辅助动力装置转子材料属性

2.2 网格划分

使用有限元软件Hypermesh进行转子网格划分，并将网格模型导入Workbench中进行计算。划分完成的转子网格模型如图3所示，共计157 860个单元、209 055个节点。

图3 转子网格模型

2.3 约束及参数设置

将网格模型导入Workbench软件中，该软件可以通过设定容差来识别距离较小的面，并创建接触。在有限元软件Workbench中使用Point mass添加简化叶片的质量及转动惯量参数。Workbench软件中提供轴承工具，可以定义两个垂直方向的径向刚度以及交叉刚度，阻尼大小也可以根据实际情况添加。使用Bearing在模型轴承装配处创建两个轴承，本文模型中的两个轴承都为球轴承，此处定义两个垂直方向的径向刚度为2.62×107N/M，由于球轴承阻尼极小，此处可忽略不计。添加叶片集中质量与轴承如图4所示。

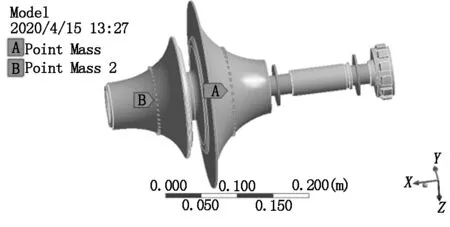
图4 添加叶片集中质量与轴承

3 模态计算

模态分析主要用于计算结构的固有频率和振型，目的是在产品的设计阶段选择合理的结构来避开固有频率，或者说最大可能地减小外界激励与固有频率的接近程度来达到产品减振的目的。模态分析是结构承受动载荷结构设计中的重要参数，也是进行其他动力学分析如谐响应分析、瞬态动力学分析和谱分析的基础[5]。

零转速下对转子模型进行模态计算，计算得到的前3阶弯曲振动固有频率及振型如表3和图5所示。

表3 转子模型前3阶弯曲振动固有频率及振型

图5 辅助动力装置转子模态振型

模态分析后，提取的振型只表示转子是如何变形的，也就是变形之后各位置的弯曲趋势，是一个相对变形，而不是真正意义上变形量的多少。从无阻尼自由振动微分方程来看，振型就是求解特征值对应的特征向量，是一个变形比例。

当激励与转子系统的固有频率相接近时，会发生共振，因此转子的激励频率应尽量避开转子系统的固有频率，防止振动过大造成破坏。

4 临界转速计算

转子各阶固有频率随转速变化规律图即为Campbell图，查看转子的振型对通过Campbell图甄别转子的临界转速具有重要意义。

转子前5阶固有频率数值相近(包括弯曲、扭转及刚体位移)，为防止Campbell图计算绘制时发生频率错位，在转速<20 000 r/min时取计算步长为1 000 r/min，转速≥20 000 r/min时取步长为5 000 r/min，这样计算出的结果更为精确。本文计算结果只筛选弯曲振动临界转速，如图6和表4所示。

表4 临界转速计算结果

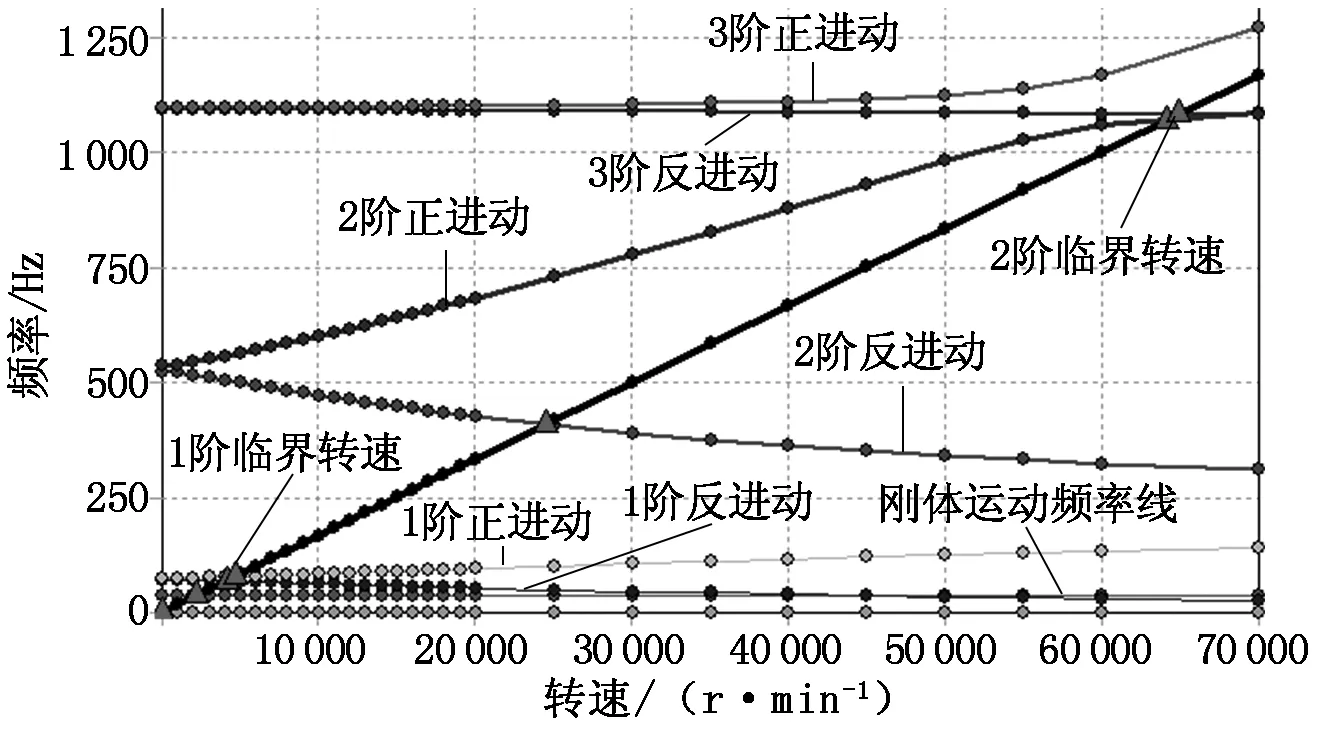
图6 转子Campbell图计算

图6中,从纵轴出发的线为转子的固有频率线，由于陀螺力矩的影响，转子在同步正进动时的临界转速会升高，同步反进动时的临界转速会降低;从原点出发斜率为1的直线为激励线，激励线与同步正进动直线交点对应横坐标的值即为转子的临界转速[6]。

转子临界转速时的振型与图5所示相似。

经计算，转子额定转速与临界转速的裕度均大于20%，转子设计安全。

5 结语

本文应用Hypermesh与Workbench软件对某型辅助动力装置转子进行了转子动力学特性计算及分析。将简化后的模型导入Hypermesh中进行有限元建模，并将网格模型导入Workbench中进行振动计算，计算得到了转子的前3阶振动固有频率及对应振型。其次考虑转子的陀螺效应，计算转子的临界转速及对应转速下的振型，并与转子额定转速做对比分析。得到以下结果：

(1)计算得到转子前3阶弯曲振动固有频率分别为71.69 Hz、523.24 Hz、1 093.3 Hz，根据振型图看出，1阶弯曲振动时涡轮端振动较大，2阶弯曲振动时压气机振动较大，3阶弯曲振动时音轮处振动较大。转子所受的外激励应避免与固有频率靠近以防止共振造成破坏。

(2)考虑转子的陀螺效应计算Campbell图，得到转子的前两阶临界转速分别为4 665 r/min与64 072 r/min。其中1阶临界转速对应的振型与1阶固有振型相似，都为涡轮端振动较大，2阶临界转速对应振型显示音轮端振动较大。转子的额定转速为45 225 r/min，与转子的前两阶临界转速都相距较远，且拥有超过20%的安全转速裕度，转子设计安全。