乘法概念的二重性及其教学启示
2021-04-02孙姝佳李明兰
孙姝佳 李明兰
[摘 要]乘法概念在小学数学学习的不同阶段多次出现,然而学生对乘法概念的掌握并不理想。从概念二重性理论对乘法概念进行分析,得出对乘法的理解应具有过程性和对象性,而且过程性意义先于对象性意义,过程性意义也是掌握概念的必要条件,而对象性意义是在操作阶段逐步反省后形成的。
[关键词]乘法;概念二重性;过程性;对象性;教学启示
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)11-0052-02
一、问题的提出
小学数学中对于乘法的学习是从整数乘法开始的,后经过小数乘法再到分数乘法,可以说乘法的学习贯穿于小学的各个阶段。如果学生对乘法概念没有一个很好的理解,那么他们对于乘法的学习将会变为机械的记忆。
比如,在学习整数乘法时,学生普遍将乘法理解为连加。如“3×5”表示3个5相加,即“5+5+5”。然而在以后的学习中,遇到小数乘法,如“1.34×2.7”时,学生便不知该如何理解这个式子。
是什么原因导致这种现象出现呢? 这涉及乘法概念的特征及对乘法概念的理解问题。本文将尝试从一个全新的角度来探讨这一问题。
二、 问题的研究——乘法概念的二重性
本文对于乘法概念的研究借助的是A.Sfard在20世纪90年代提出的数学概念二重性理论。该理论认为许多概念既表现为一种过程操作,又表现为对象结构,概念往往兼有这样的二重性。比如三角函数sinα,既可以看作直角三角形中锐角的对边与斜边之比 x/r , 此时三角函数概念被理解为一种数学运算,体现过程性特点;也可以将其当成计算的一个结果,此时概念具备对象性特点。
我们也可以将乘法理解为具有这样二重性的概念。乘法的学习是从整数乘法开始的,学生对乘法的理解局限在“连加”的意义上,而这种理解体现了一种过程性,学生仍把乘法看作几个几相加,并没有把乘法概念与加法概念做本质的区分。学生只有将乘法作为一种新的运算来理解时,乘法概念才成为一种具有结构性的对象。
巩子坤曾将对乘法概念的理解分为两部分:乘法意义的理解和乘法运算的理解(乘法运算的理解又包括对运算算理和运算法则的理解)。事实上,意义的理解体现了乘法概念过程性的一面,运算的理解则体现了乘法概念对象性的一面。
对于乘法意义的理解表现为实现乘法各个表征之间的转化。比如对于用符号表达的式子“15×4”,学生可将其理解为一种现实情境的表征:小鹏有15个玻璃球,小红的玻璃球的个数是小鹏的4倍,小红有多少个玻璃球;也可以用语言表征来叙述式子的意义:4个15相加是多少;当然也可以用连续型或离散型图像来表示式子的意义;又或是用实物操作来解释式子的含义。这些都是学生对乘法意义的理解,我们不难看出,这些表征都体现了一种操作性,是动态的、有步骤的。
而对于乘法运算的理解则是在对乘法运算算理理解的基础上,掌握乘法运算法则,从而达到对乘法概念的整体性理解,并将乘法概念看作一种不同于加法的新运算,从而将乘法概念看作一种结构化的对象。这种结构化的对象作为一种运算,不仅形成具有运算性质、运算定律等层次性和关系性的内部组织,而且能打破本身的局限性,伸展出一些“触角”,比如与其他概念(如幂运算)的纵横联系,编织成网络。
因此,对于文章开头的现象,也许我们可以归因于学生未真正理解乘法的概念,但更深层次的原因在于乘法概念具有二重性的特征,而学生只停留在乘法过程性的理解,没有将其作为一个结构化的对象。
三、进一步研究——过程性意义先于对象性意义
学习一种运算,首先要让学生理解运算的意义,因为只有理解了运算的意义,才能知道何时使用这种运算,也才能从意义出发推导运算的法则。加之上述对乘法概念特征的分析不难看出,乘法概念过程性意义的学习确实应先于对象性意义的学习。
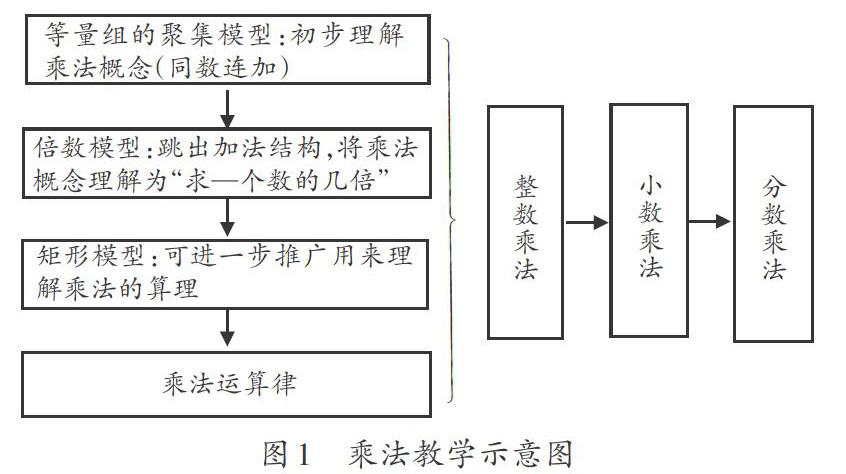
闫云梅等人曾在论文中分析乘法的现实模型,提出了实现乘法概念建构的教学建议。笔者整理分析得出如图1所示的教学示意图。可以看出,对于乘法概念的学习需经历两次建构,第一次建构从乘法的现实模型中逐步实现;第二次建构通过数系的扩展来实现。
对于第一次建构,是经历多种现实模型后逐步实现的,刚开始对乘法概念的理解依靠于现实情境,这具有操作性特点;经过“同数连加”,到“加法结构转变为乘法结构”,再到慢慢理解算理,直到最后总结出乘法运算律,乘法概念才开始成为一个较完整的对象。这个转变不经一定数量的操作是得不出本质规律的,更无法将概念发展成为对象,因此过程性意义要先于对象性意义去掌握且很有必要。
第一次乘法概念的建构为小数乘法、分数乘法的学习奠定基础,随后通过数系的拓展,又将乘法概念的系统做了第二次完善。如果在整数乘法的学习中没有理解到概念的对象层面,那么学生将无法理解小数、分数乘法的意义,对运算法则的学习也将变为机械记忆。对于“1.34×2.7”这个式子,只有经过对象化过程后,不再将乘法看作“连加”的过程,而是依照乘法运算规律,将乘法看作一种新的独立的运算,才可以从乘法分配率来抽象理解这个式子,或者从乘法的“因数的变化引起积的变化规律”来形式化理解这个式子。
可见,乘法概念具有过程性和对象性,对这两个层面的理解并不矛盾。过程性意义先于对象性意义,过程性意义是掌握概念的必要条件,而对象性意义是在操作阶段逐步反省后形成的。
四、教学启示
1.重視乘法概念的教学
过程与对象同属于乘法概念的两个侧面。概念学习中, 过程与对象的作用同等重要, 二者不可偏废。对乘法概念的教学若不重视从过程性过渡到对象性,学生很难利用乘法的性质来解决问题。根据巩子坤的研究,事实上也确实如此。尽管课堂上有对学生从过程到对象的引导,但学生在独立解决问题时仍倾向于直接进行运算,或直观给出解释,而非用乘法运算规律进行理解。这说明当前我们对于乘法概念的教学不够重视,学生仍局限于对运算法则的机械记忆,还未从根本上将乘法概念作为一个对象。因此,教师应进一步重视乘法概念的教学。
2.注重从“过程”到“对象”的螺旋上升
乘法概念在小学数学学习的不同阶段多次出现,我们要注意乘法知识的螺旋上升,逐步深化学生对概念的理解。在低年级,乘法从几个相同的数相加开始学习,后来随着学习的数越来越大,直到引入乘法的竖式计算,这时教师会对学生解释竖式计算的算理,使学生初步了解乘法运算的规律并总结出乘法运算律,对乘法的理解也逐渐从过程上升到对象。进入高年级,在学习了小数、分数后,学生又进一步理解数系扩展后的乘法意义,将整数乘法运算规律类比到小数、分数乘法的学习中,同时补充“乘法也表示一个数的几分之几”的过程性意义。从微观看,对于同一个概念可能会得到不止一个“过程—对象”的区分方式。
3.使学生形成良好的概念体系
对概念的理解形成体系,不仅有利于形成具有层次性、关系性的内部知识,且易发现概念与外部知识的关系,从而形成更大的知识网络体系。事实上,作为对象的概念,在某一个层次和更高一级层次之间起着一种枢纽作用:它既操作别的对象,又被高层次的运算来操作,也就是说,对于成为对象的概念更容易形成概念系统,从而更利于整体把握知识。因此,教师应注重让学生形成良好的概念体系。
[ 参 考 文 献 ]
[1] 李士锜.熟能生巧吗[J].数学教育学报,1996,5(3).
[2] 巩子坤.有理数运算的理解水平及其教与学的策略研究[D].重庆:西南大学,2006.
[3] 李士锜. 熟能生笨吗?:再谈“熟能生巧”问题[J].数学教育学报,1999,8(3).
[4] 人民教育出版社小学数学室.小学数学教材教法(第二册)[M].北京:人民教育出版社,2001.
[5] 闫云梅,刘琳娜,刘加霞.小学阶段乘法的不同现实模型分析与教学建议[J].课程·教材·教法,2014,34(3).
[6] 佘文娟,王光明.也谈A.Sfard数学概念的二重性理论[J].数学通报,2013,52(8).
(责编 罗 艳)
