浅谈促进理解的数学教学
2021-04-02周卫东
周卫东
[摘 要]“为促进理解而教”是国际认可的数学教学的理性追求。以“小数的意义”教学为例,具体阐释一些行之有效的“促进理解”的实践策略:通过探明原理、经历过程、多重联系,让学生明晰“理解什么”,让学生卷入“怎么理解”,让学生实现“理解深刻”。
[关键词]为理解而教;原理;过程;关联
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)11-0013-03
认知心理学提出:“理解实质上就是一个学习者以信息的传输、编码为基础,根据已有的信息建构内部心理表征,进而获得心理意义的过程。”与一般的“理解”相比,数学理解具有典型的学科韵味。首先,理解的对象是数学的概念及其关系,理解意味着对数学概念的内涵和外延的准确把握,對概念之间相互关系的清晰认识。其次,数学理解是过程与结果的统一。从过程方面看,数学理解是学生与数学知识沟通对话,相互融合,不断成生新的认知结构的过程。从结果方面看,数学理解则可以看成是学生数学学习的一种“获得”,是外在的数学结构在个体心理上的投射。
基于以上认识,教师在教学中需要把握数学的本质要素,突出意义的建构过程,使得学生习得数学知识的关联与闭合,从而实现对数学的真正“理解”。
一、探明原理,让学生清楚“理解什么”
英国学者P·欧内斯特说过:“数学教学的问题并不在于寻找最好的教学方式,而在于明白数学是什么,如果不正视数学的本质问题,便永远解决不了教学上的争议。”一般认为,数学知识的本质,既表现为隐藏在客观事物背后的数学知识、数学规律,又表现为隐藏在数学知识背后的本质属性。数学教学教什么?毋庸置疑,摆在第一位的一定是教学内容的本质和内涵。
如小数的意义是什么?追根溯源,小数并不是因改写分数而产生的,而是自然数的十进位值计数规则加以扩展的结果,它是以10的n次幂为分母的另外一种表示形式,是十进制计数向相反方向衍生的结果,其本质就是十进制分数的另一种表现形式。小数和整数在形式上是统一的,小数的出现也使十进制计数法从整数扩展到分数,数的内涵更加丰富了。数的形式改变了,但其中不变的是相邻两个计数单位之间的进率还是10。
“小数的意义”怎么进入学生的视野呢?可以生活中常见的测量身高现象为载体构造情境串。第一则情境是 “小军的身高是1.4米”,让学生思考“这里的1和4分别表示什么”,使其明白,这里的“4”是4格,表示把1米平均分成10份,取了其中的4份,表示0.4米,接着以此为基点逐渐建立起一位小数的基本含义,即“一位小数表示十分之几”;第二则情境是“半个学期后,小军再一次量了身高,身高在1.4与1.5米之间,你能想出办法知道他现在的身高吗?”,引导学生进一步理解“可以把1.4与1.5之间继续平均分成10份,现在高出3小格,每一小格是0.01米,即现在的身高是1.43米”,并在对大量素材的比较中建立起两位小数的意义,即“两位小数表示百分之几”;然后,以大问题“你觉得还有几位小数?请你任选一个两位以上的小数,利用表格或纸片进行研究”驱动学生到达一个更大的空间之中,任学生的思维自由驰骋,使学生在自我感悟、全班共研的环境中理解更多位小数的意义。
“小数的意义”还可以怎么进入学生的视野呢?可以创设在图1中画“0.46”的大问题,让学生的思维一次又一次处于“悱愤”之中。对于画0.46,大多数学生都会想到要涂的是比4格多一点,但多多少呢?学生在深度探索中逐渐明白:可以将第5格再平均分成10份,涂其中的6份。教师进一步提出:“同一幅图中出现了两个计数单位,怎么才能统一计数单位呢?”从而得出更为精确的网格图——将正方形平均分成了100份,这样,计数单位悄悄变化,凸显了相邻十进制计数单位之间的关系,进而引出两位小数的意义。如此设计,学生在理解一位小数意义的基础上进行已有学习经验的正向迁移,通过一系列的追问,学生将已有的十进制知识进行再创造,经历“做”数学的过程,建构两位小数对应的概念表征,理解了两位小数的意义。
二、经历过程,让学生卷入“怎么理解”
让学生自己建构数学,既是教学的目标,也是学生理解数学的方式。若只有教师教,没有给学生学习关键思想和关联点的机会,学生的理解就无从谈起。因此,发展学生的数学理解,重要的是让学生经历学习的过程,让学生自己建构数学知识。弗赖登塔尔认为,数学的根源在于普通常识,数学实质上是人类常识的系统化。因此,每个学生都可以在一定的指导下,通过自己的实践活动来获得这些知识。
强化“变式”。比如,在学生初步理解了一位小数的意义后,可以让学生通过折一折、画一画正方形纸片等方法表示0.3;在学生深入理解了一位小数的意义后,再让学生拿出之前的那张正方形纸片,描绘想研究的一个两位小数。教师对学生作品进行逐一评析,让学生明白,无论画的是一维的线段还是二维的平面图形,只要把它们平均分成10份、100份,其中的几份都可以用小数来表示,促进学生进一步理解和深化小数意义。
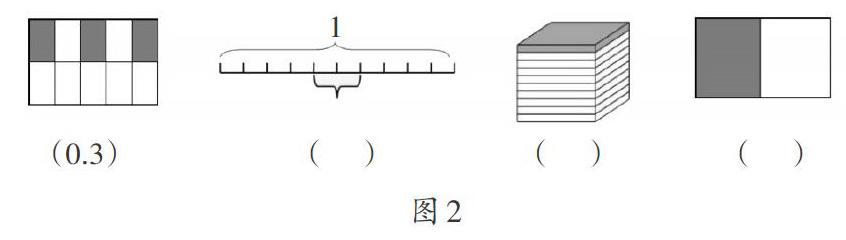
又如,教学一位小数的意义之后,还可以编拟如下的练习题,使学生的理解“发生”。
第一幅图没有“老老实实”地按顺序涂三个格子,而是间隔着涂;第二幅图是线段,0.2是截取中间的一段,打破学生的思维定式;第三幅图是立体图形,拓展了“1”的外延,发展学生的空间思维;第四幅图不是平均分成10分,可启发学生思考:“如果看不到平均分成10份,还能用小数表示吗?”使学生打破思维定式,触及知识的本质,即无论看不看得到平均分成10份,涂色部分都可以用小数来表示。
丰富“表征”。每一个抽象的数学概念,都可以有不同的数学表征。不同表征之间的“互译”,可以丰富学生对概念内涵的把握和洞察。因此,教师要鼓励学生用“自定义”的形式表征他们的数学观点,让不同的表征方式之间产生丰富的联系,有利于学生形成丰富的概念意象,促进学生深入理解数学知识。比如,让学生在线段、长方形和长方体三种图形中任选一种来表示0.7、0.23和0.575,从而使其明白:数学知识内部的发展是有规律可循的,尽管每一种图形都可以表示多位小数,但是平均分成10份、100份、1000份,分别对应一维的线段图、二维的平面图和三维的立体图会显得更方便些。又如,让学生在方格纸上画出“0.46”。怎么将第5份平均分成10份?有学生横着分,也有学生竖着分,教师引导学生对两种表征方式进行对比,在肯定都有道理的前提下,引导学生感知横着分的优势更明显:既美观又明晰,更方便把整个正方形平均分成100份。
三、多重关联,让学生实现“理解深刻”
哈佛大学威金斯教授认为,理解不是单方面的成就,而是多方面的,可以通过不同类型的证据表现出来。“真正的理解”可以在六个方面得以体现,即能结构、能解释、能应用、能洞察、能深入、能自知。这六个方面为评价学生的数学理解提供了多元指标的同时,也指出:数学教学不仅要关注知识的客观性标准,也要关注学生在理解数学时的个性化活动。
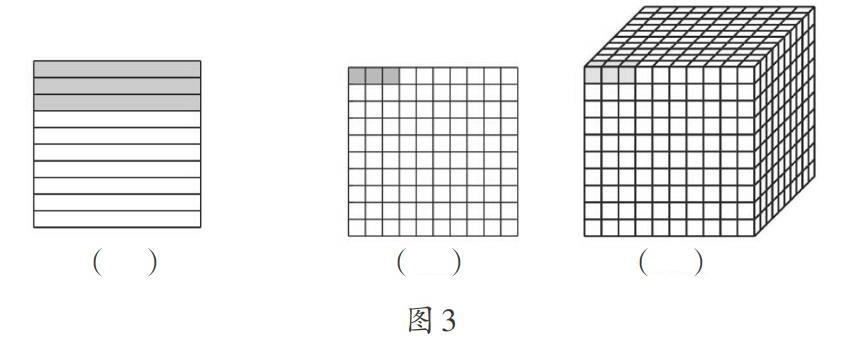
纳入结构。一般情况下,学习过程只能按时间顺序先后安排,但理解却并不是直线式的简单累积,相反,它是螺旋式地发展、结构式地建造出来的。对于数学来说,无论是一个概念的形成,还是整体认知结构的产生,都需要经历一个建构的过程。用皮亚杰的话说,就是 “每一个结构都是心理发生的结果,而心理发生就是一个从较初级的结构过渡到一个不那么初级的结构。”因此,理解不仅仅是把新知识与已有的旧知识产生联系,而是创建了一个丰富的、整合的知识结构。比如,让学生观察图3,填空并思考三个图之间的联系:
又如,通过将同一个正方体依次平均分成10份、100份、1000份后所得到一份的量(如图4),让学生感受不同计数单位1、0.1、0.01、0.001,感受一位小数、两位小数与三位小数的研究模型及其计数单位之间的关系。
促进阐释。面对不同的问题,人们通常会采取不同的思维方式。基于真实任务的问题解决将学生在学校的学习视为“现实世界中创造性社会实践中完整的一部分”,对促进学生的数学理解具有重要的作用。真实任务能为学生提供一个促进知识向日常生活转化的实践场。在这一实践场中,知识、思维和学习的情境是紧密联系的,学生的信念、经验和已有知识构成解决问题的概念工具。一位教师就设计了一道很有价值的现实问题:“正在上四年级的小马在学校参加了体检,回家后妈妈问他身高是多少,小马回忆了一会儿,说:‘我的身高是这样的一个小数,这个小数里,有数字9和4。那小马的身高是多少呢?”学生在有趣且富有开放性的问题中,运用已经理解的小數意义进行解释和应用,自然有效地建立了数学与生活的紧密联系。还有一位教师在结课阶段围绕“有了分数为什么还要学习小数呢?”这一思辨性很强的问题,让学生用分数与小数两种表示方法进行计算,从而感受到用小数计算比用分数计算更加快捷与简单,进而领悟到小数诞生的必要性。
教学有法,但教无定法,诚如帕斯默尔所说:理解具有多种多样的表现方式,这些方式彼此相互独立又相互交融,相应地,也有许多不同的教“理解”的方法。期待数学教育因理解而拥有更多的变化与活力。
(责编 金 铃)
