深度理解：探索从“定量”走向“定性”

丁洪

[摘 要]数学学习离不开“定量”和“定性”。其中，侧重行为操作的“定量刻画”，通过问题驱动、知识迁移和对比展示，实现初探激趣、再探体验和深探建构，助推线性理解的发生;侧重思维操作的“定性把握”，通过分类定性和分层定性，实现二维理解和多维联系，助推结构理解的生发。最终，实现探索活动的温度可感、广度可拓和深度可测。

[关键词]深度理解;面积变化;探索规律

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）11-0011-02

人们认识和理解客观世界一般需要经历两种过程，即定量刻画、定性把握，前者侧重行为的操作过程，比如画图、测量和计算等，这些外显行为处在学习的准备阶段，具有客观性、现实性和基础性的特征;后者侧重思维的操作过程，比如猜测、验证、概括等，这些内在行为处在学习的生发阶段，具有主观性、探索性和创造性的特征。显然，数学学习就是要从定量刻画逐步走向定性把握，逐渐抽象概括、形成方法和模型，进而广泛应用。

“面积的变化”是苏教版教材六年级下册安排的“探索规律”的专题活动，属于“图形与几何”板块。从行为操作来看，“面积的变化”聚焦简单图形，按照一定大小的比例，锁定影响图形变化的关键因素，使学生顺利画出放大和缩小后的图形，进一步培养学生的空间观念;从思维操作来看，“面积的变化”主要引导学生经历“猜想与验证”的过程，发现图形面积变化的一般规律，初步渗透科学的方法理论。问题是，探索如何“立序”，研究从哪个图形开始？探索如何“立行”，每个图形研究的侧重点是什么？探索如何“立言”，怎样表达研究的结论？应该说，起点可以不同，过程存在差异，但是深度理解的追求必定殊途同归。

一、定量刻画：在行为操作中线性理解

著名物理学家杨振宁教授认为：“除非有定量的实验证据，没有任何一种哲学性的讨论能够作为科学的真理來加以接受。”也就说，一方面数据产生需要定标准、去测量和得结果，研究不能忽视统一性和准备性;另一方面，研究需要用数据来“说话”，研究结论才具真实性和普适性。

1.问题驱动，初探激趣

这个环节的教学一般有两种版本。第一种是以长方形的探索为起点，要求学生“分别量出它们的长和宽，写出对应边长的比”，并记录“大长方形与小长方形长的比是（）∶（），宽的比是（）∶（）”，然后引导学生“估计大长方形与小长方形面积的比是几比几” 。学生通过画图法、计算法和列表法，以及积的变化规律验证猜测，得到“大长方形与小长方形面积的比是 9∶1”。教师顺势提出问题“其他平面图形按比例放大后，面积的比又会怎样变化呢？”，驱动学生继续思考。第二种是以探索正方形为起点，引导学生聚焦正方形边长的前后变化，以及对应面积的前后变化，再提炼出相关结论。

显然，从长方形出发的探索，遵循的是知识的建构序列，毕竟面积起始图形的作用不容小觑;从正方形出发的探索，贴近面积累加的计量规则，所得过程与结论更直接和更直观。

2.知识迁移，再探体验

首先，借助媒体的动态演示，将正方形（或者长方形）、三角形和圆分别按比例放大，并在活动单上呈现放大前后的两类图形，学生通过指认、联系和对比，明确了将要探索的数学对象。其次，通过问题“研究图形的变化规律需要知道哪些信息？”，让学生锁定影响图形面积大小的关键因素，即边长、长和宽、底和高、半径，清楚探索的测量重点。其次，借助问题“上面的图形分别是按几比几放大的？图形放大后与放大前的面积的比各是多少？”，鼓励学生组内分工，自主选择喜欢的图形进行探索，并将测量和计算的结果记录在表格中，明确探索的操作要点。最后，利用问题“比较每个图形放大后与放大前的长度比和面积比，你能发现什么规律？”，引导学生观察、对比，最终发现“长度比是 2∶1，面积比是4∶1;长度比是 3∶1，面积比是9∶1……”“两个比的后项都是1，面积比的前项是长度比前项的平方” ，顺势归纳、总结和抽象出“如果把一个图形按n∶1 的比放大，放大后与放大前图形的面积比是 n2∶1 ”的数学模型。

显然，这是本课的重点部分，是知识建构、探索成效和情感共鸣的关键阶段。其中，教师的指导和帮助不能缺位，比如必要测量的方法指导，充分活动的时空保障，理性表达的适时参与，等等。也就是说，只有师生心中都有“数”，才能助推探索实现从特殊到一般的思维跨越。

3.对比展示，深探建构

从科学方法论的角度来看，猜测的结论是需要验证的，而且是需要多个案例、多种角度和多种途径的验证，因此，以点带面、以此类推就成为探索的常用手段和通用方法。这样看来，教材精心设计的“在方格纸上画一个平行四边形，按比例放大，算一算放大后与放大前图形的面积比，看看是不是符合上面发现的规律。”的探索活动，是及时的、应景的和必需的。具体到活动中，一方面要鼓励学生组内分工协作，图形放大的比例可以各不相同，通过对比和分析数据，验证规律的适用程度，建构探索学习的回路;另一方面，鼓励学生逆向思考，并通过对比、分析和归纳案例数据，得到“如果把一个图形按 1∶n 的比缩小，缩小后与缩小前图形的面积1∶n2 ”的数学结论。当然，教学还可以更进一步，引导学生超越图形的变化方向，再次从数量上归纳并发现“面积比与长度比的平方倍有关”。

显然，先从特殊到特殊的类比思考，实现了知识迁移;再从特殊到一般的归纳思考，建立了数学模型;以平行四边形的面积变化为例，在不断变化中感知不变的存在，又验证了规律可信。进一步说，图形变化的程度有了定量刻画这个利器，就能将模糊的感知显性呈现，方便了描述交流。

二、定性把握：在思维操作中结构理解

定性就是要将研究对象内在的、稳定的、持久的倾向与外在的、易变的、暂时的倾向区分开来。这样处理，一方面能帮助学生探索未知的经验，另一方面也能帮助学生反思已有的经验。最终，实现对研究对象的整体的、结构的和系统的理解，进而把握其本质。

1.分类定性，二维理解

像长方形、正方形、平行四边形、三角形、梯形和圆形，它们都是基本的平面图形。影响这些平面图形面积大小的关键因素都有两个，它们的名称虽然不一样，但是都体现了二维空间的图形特征。在定量刻画环节，主要是测量具体图形的具体数据，有了这些数据的感性支撑，就可以脱离具体数据，从整体上加以理性探索。

师：将这些图形按照n∶1 的比例放大，不进行具体测量，你能推理得到面积变化的规律吗？试一试。

生1：我研究的是长方形。原来的面积是S=a×b=ab，现在的面积是S=na×nb=n2（ab），我发现“长方形现在的面积∶原来的面积=n2∶1”。

生2：我研究的是三角形。原来的面积是S=a×b÷2，现在的面积是S=na×nb÷2=n2（a×b÷2），我发现“三角形现在的面积∶原来的面积=n2∶1”。

生3：我研究的是圆形。原来的面积是S=πr2，现在的面积是S=π×nr×nr=n2（πr2），我发现“圆形现在的面积∶原来的面积=n2∶1”。

……

显然，平面图形中两个维度的线段分别扩大n倍，对应的面积就扩大了“n×n=n2”倍。也就是说，图形的样子可以不一样，但是图形结构的属性相同，所以变化的结论内在一致。如有可能，思维还可以引向一般建构，即两个维度的线段分别扩大a倍和b倍，对应的面积就扩大了“a×b=ab”倍。可以看出，這样的思维操作更通透、更舒展和更理性。

2.分层定性，多维联系

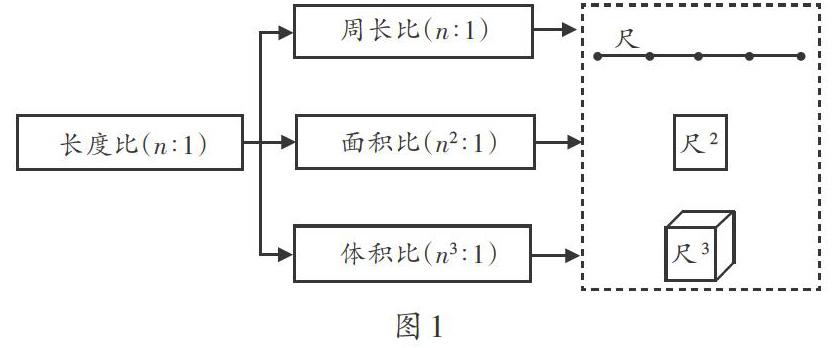
通过问题“回顾探索规律的过程，你有什么收获？还想到了什么？”，驱动学生从变化特征、探索方法和结构联系等层面进行界定。首先，是变化特征的界定，变化分为按比例放大或者按比例缩小，影响图形变化的两个维度“同步变化”，但是图形样子“始终不变”，变中不变演绎了图形内外的辩证统一;其次，是探索方法的界定，引导学生总结“要认真观察、比较数据，才能发现规律”。数据可以是具体的或者是抽象的，但是数据建模的规律是一样的，虚实结合演绎了感性和理性的辩证统一 ;最后，是结构联系的界定，通过猜测“长方体、正方体等按比例放大后，体积比和长度比会有什么关系”，引导学生从联系的视角尝试阐述，并逐步发现：一维图形是线段的同步变化，二维图形是线段的变化组合，三维图形是线段的变化建构（如图1）。结构生长演绎了部分和整体的辩证统一。

显然，定性研究既需要回到原本事实和经验本身，从具体图形出发探索;又需要超越经验和事实，将图形归置定性为某种类型，并再次出发探索;最后通过类别归属定性在某个维度，上升至理性认知和一般思考。可以看出，这样的思维操作既演绎了知识的追本溯源，又实现了知识的螺旋建构，使得探索活动温度可感、广度可拓和深度可测。

[本文系江苏省教育科学“十三五”规划重点课题“基于问题链驱动的小学生数学化学习的研究”阶段性成果（课题批准文号：C-b/2020/02/26）。]

（责编 金 铃）