向学重构:小学数学单元整体教学的策略思考
2021-04-02徐晓良
徐晓良

[摘 要]针对学生不同的学习起点,遵循教材的知识逻辑,提出了小学数学整体教学的两大策略:一是向学解析,甄别剖析学生的学情与教材内容的关联;二是向学重构,构建联结更迭的“二维四重”样态,实现深度学习。
[关键词]向学重构;单元;整体教学;策略
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)11-0018-05
小学数学教材内容是以单元为最小单位编排的,每个单元相对独立又相互联系,但由于目前省、市、县、校级的教研活动通常都是以课时为单位活动为主,较少开展以单元、主题、模块为单位的结构化研究与实践,因此缺少了对课程内容的整体把握和结构化的处理。当然,一切教学活动的落脚点在于学生,“以生为本”是教学遵循的起点。只有坚持学生立场,整体分析学生与单元学习材料,找准学习起点,确定单元学习主题,设定单元目标,重组学习内容,形成整体学习规划,才能实现深度学习,培养学生的数学高阶思维能力。
一、向学解析:甄别学情与筛选教材的“二析”路径
(一)学情甄别分析,精准把脉学生
1.分析学前预习单
通过分析单元中的每一个预习单,诊断学生学习本单元的难点、障碍点,以及學生学习本单元知识的相关思维水平。以四年级“鸡兔同笼”为例:
通过调查发现,学生两极分化严重。参加课外补习班的学生能立刻用假设法解决;没有接触过的学生无从下手。
2.分析学后评价单
学后评价单能为教师后续教学提供客观的数据。学后评价单包括专项评价单、课后作业、单元测试等。以三年级“分数的初步认识”为例:
学生做题的正确率只有50%,学生基本上是用方程和分数除法来解。错误的原因主要是找错等量关系,值得注意的是:三年级的5名学生中有3名通过画线段图、利用分数意义解题。因此,这个问题一定与三年级和五年级的分数教学有关。
(二)内容关系分析,精确剖析关联
1.依内容形成要素,理知识层次
分析单元整体教学的教材,除了要挖掘知识内容的本质与核心外,还要充分关注单元内容要素的形成关系。内容要素之间的形成关系,主要是说明不同的知识点之间的联系,知识点之间有怎样的支撑关系,也能够呈现学习内容的编排思路,折射出知识内容背后所蕴含的核心思想与观点。在此基础上,可将单元主题内容分为四部分:近似性知识、递进性知识、拓展性知识和思想类知识。
2.依单元知识关系编结构图
知识结构图能清晰地呈现单元知识间的关系,或递进,或并列,或包含,等等,将单元知识间的关系通过图示的形式记录,以便为单元重构教学的设计提供一手资料。
单元知识呈并列关系:有些单元之间的内容呈并列关系,如二年级“表内乘法”,2~9的乘法口诀呈并列关系,在2个不同单元进行教学,如图1所示。
单元知识呈递进关系:教材中的许多内容是递进关系的,前面知识是为后续知识作铺垫,后续知识是前面知识的延伸,比如三年级“分数的初步认识”(如图2)。
单元知识呈包含关系:数学概念本身就有包含关系,如正方形与长方形之间、平行四边形和四边形之间、等式和方程之间等,都存在包含关系。
二、向学重构:联结更迭结构与思维的“二维四新”样态
(一)基于学情甄别下的目标重构
单元目标重构是指在分析学生学习基础、认知规律与思维特点的基础上,结合单元教材分析,综合考虑单元知识与技能的学习要求、知识之间的逻辑关系结构、基本活动经验,重新拟定单元教学目标,重构学习过程。
1.把握认知结构的单元重构
基于认知结构的单元重构遵循学科知识逻辑与学生认知逻辑相吻合的原则,在分析教材单元内容基础上,根据学生的认知结构,采用同化的方式重组单元教学内容,拟定单元目标,实现深度学习。
如人教版教材一年级上册“数的认识”领域分成“1~5的认识和加减法”“6~10的认识和加减法”“11~20各数的认识”三个单元,纵向打通这三个单元,形成“数的认识”和“数的运算”的两个独立的学习主题。这样的重构,能打破原有的逻辑结构,放大认知背景,通过同化的作用,使深度学习真正发生。(见表1)
这样的单元重构基于两个认识:一是有利于学生的认知结构的拓展;二是有利于学科逻辑与学生逻辑相融合。重构后,有效地将学生认识数的过程和符号化过程融合在一起,用“类化”结构打通学生未来对大数的学习。
2.明确思维特点的单元重构
明确思维特点的单元重构是根据单元学习内容,结合小学生的思维发展特点,即以具体形象思维为主要形式向以抽象逻辑思维为主要形式过渡,找准两者之间的吻合点,重新拟定单元学习目标,使具体知识内容背后的数学思维方法与学生思维特点切合。
将“分数的初步认识”从5课时教学重构为6课时,分成“数量”与“关系”两部分。从量的学习再到关系的抽象,将学习内容紧贴着学生的思维。如图3,在分数与除法(认识几分之一)、用分数表示图、给分数配图、画图比较大小、表象图计算、分数问题与整数除法问题这6课时的教学中,让学生充分地认识、理解分数的三层含义:分数不仅是一个数,它还能反映平分的过程,还能表示两个量之间的关系。
重构后的单元符合三年级学生从具象思维向抽象思维过渡的特征,丰富了分数的维度,使得学生具备了辨析分数“量”与“率”双重含义的能力,为后续学习打下扎实基础。
(二)基于学情甄别下的学法重构
学生学习起点、学习基础不同,学习的内容不同,学生的学习方法也是不同的。本研究主要采用单元序列法与辐射法的重构,实现学生深度学习。
1.单元序列法重构
单元序列法重构是按知识发生发展的序列进行重组的方法。把单元看作一个整体,结合课时具体的教学内容,围绕单元主题进行前沿后伸,充分运用知识迁移,厘清内在逻辑关系,准确把握教材的知识内核,促进学生高阶思维成长。
如“小数的初步认识”与“小数的意义”,许多教师在教学这两个单元时存在界线不清的问题,究其原因,教师没能较好地厘清这两个单元之间的内在序列。下面就对小数的这两个单元做学习序列上的重组。
2.单元辐射法重构
单元辐射法重构是指紧扣单元核心目标,聚焦单元核心知识,并向周边发散,形成以核心带动整体的辐射效应。厘清单元知识脉络,建构知识核心源,进行思维迁移发散,领悟知识间的联系,对知识点背后蕴藏着的数学思想、核心本质有整体认知。
如二年级“乘法口诀”的内容:乘法的初步认识,2~6的乘法口诀,乘加和乘减题,用所学的计算知识解决问题;第六单元教学内容:7、8、9的乘法口诀、乘法口诀表以及用7~9的乘法解决简单的实践问题。对学生学情与教材分析后,发现以下三个问题。
一是内容的结构编排同一性。教材按从小到大、从少到多来编排乘法口诀单元。教学若是从开头到结尾都是一个“面孔”,学生会对学习口诀容易产生厌烦情绪,失去学习动力。
二是内容的梯度层级不合理性。教材是按1的口诀有1句,2的口诀有2句,3的口诀有3句……来编排的,口诀越学越多。随着口诀的增多,难度的加大,学生的学习信心逐渐降低。
三是编排顺序对灵活解题造成局限性。对于教材中“填未知因数和最大能填几”的习题,例如( )×6<50,对于 6的口诀,学生只学到六六三十六,因此感觉解题困难很大。
辐射结构的学习,首先是确定核心,再通过核心的重点研究,向相同学习内容辐射。乘法口诀分三段,第一段就是学深学透5的乘法口诀;第二段,放手让学生自主推导2、3、4的乘法口诀;第三段,在灵活运用中学习6、7、8、9的乘法口诀。每一段都是以理解乘法的意义为基础,如图4所示。
通过整合重组,以5的乘法口诀的学习为核心,向其他口诀学习辐射,可以看到乘法意义的生长过程,更看到学生思维的增长。重组后,学生对数学本质理解更深,高阶思维能力更强。
(三)基于内容筛选下的知识重构
基于内容筛选下的知识重构能够有效链接学生立场与学科逻辑,构建更有整体性、关联性的学习板块,实现结构化的任务设计。重构的途径有以下两条。
1.单元聚焦整合重构
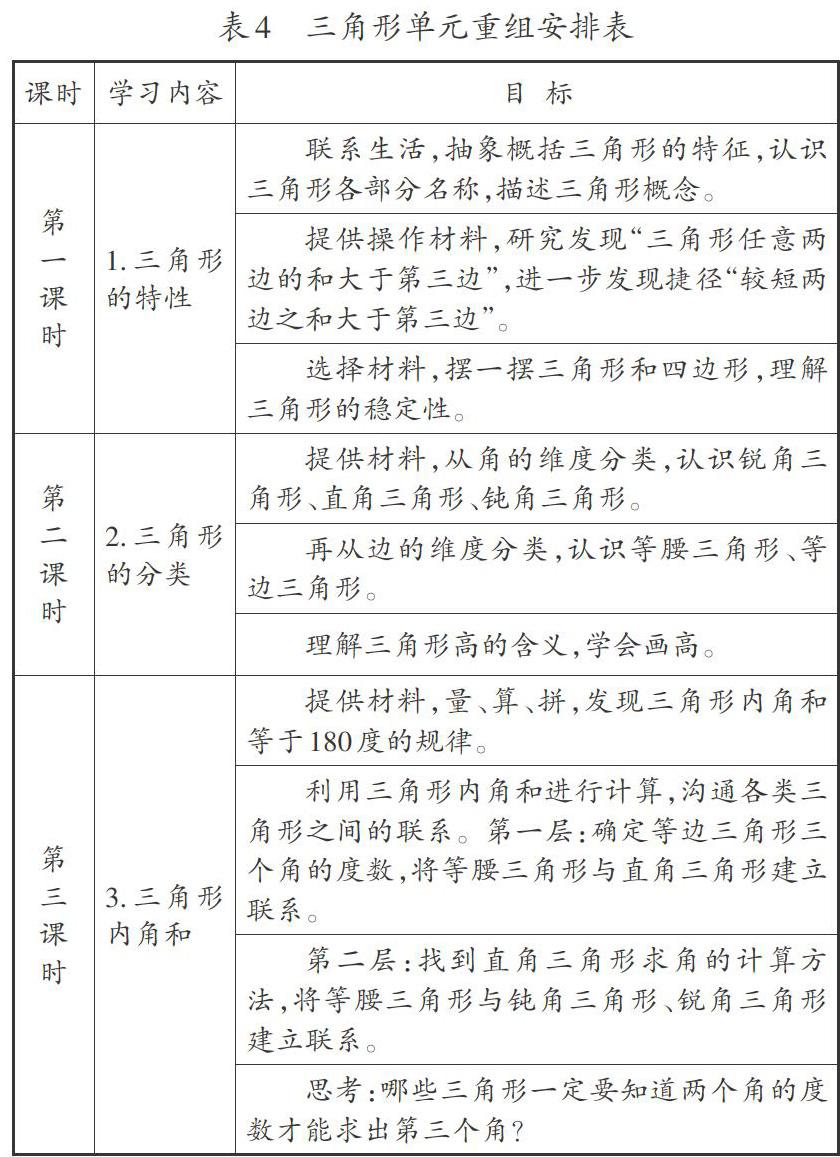
单元聚焦整合重构,是指打破單元原有编排,聚焦学习难点,突破重点,分层推进,实现“结构化”。以四年级“三角形的认识”单元为例,内容太散,主要表现在三个方面:一是过于强化简单概念。第一课时就是认识三角形,许多教师让学生经历了一个较长的建构过程,但学生兴趣不浓。二是“高”聚焦不够。三角形的种类很多,高的情况也纷繁复杂,在第一课时就让学生在没有充分认识三角形的基础上画高,对学生来说自然有难度。三是两种特性认知混淆。第一课时的三角形的稳定性与第二课时的三边关系的稳定性,学生容易混淆。
本单元的重组要聚焦三角形学习难点,理顺学生的认知逻辑与学科逻辑,将新知识链接成一个系统化的整体内联网。以下是三角形单元重组后的安排分布。(见表4)
这样的编排方式使4课时变成3课时,难点突出,顺应学生认知逻辑的发展。
2.单元梯度拓展重构
梯度拓展重构是指单元主题挑战性更高,需要顺应学生的学习方式,增加学习内容的层次性,给学生充分思考与实践的时间,培养学生的核心素养。
如“鸡兔同笼”单元,依据前测提出以下重组设想。
一是回归学生起点,人人掌握“列举法”。呈现非典型“鸡兔同笼”问题,让学生从未知开始,尝试利用列举解决问题。学生在解决问题的过程中积累经验,形成有序思考,以及观察、分析、归纳、创新等综合能力。
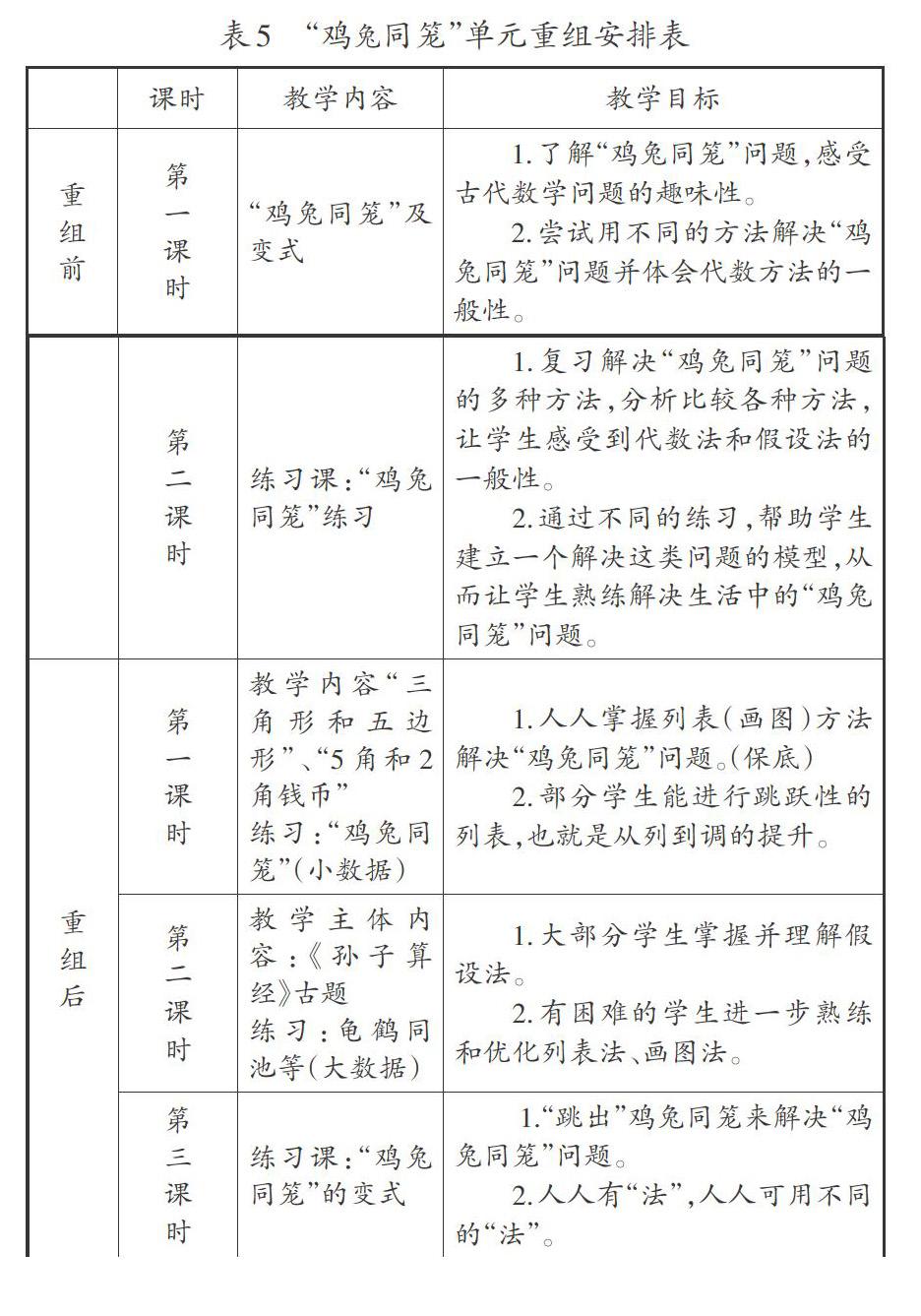
二是拉长体验过程,深度理解“假设法”。面对两极分化相对比较严重的“鸡兔同笼”问题,拉长体验的过程,能给假设法做更深更厚的铺垫。将原来的2课时(“鸡兔同笼”+练习课),重组为3课时(“鸡兔同笼”1+“鸡兔同笼”2+练习课)。(见表5)
通过重组,构建了适合不同学生的学习序列,降低了学生的学习难度,促进学生深度理解。
(四)基于内容筛选下的结构重组
教材中相同领域的内容的编排存在一定的关联,这些内容有些相近或相似,有些呈递进关系,在设计教学时可以根据学生的学习特点,找出这些内容的关联处、相似点,然后进行重组。
1.近似性结构重组
近似性结构重组就是找到线状脉络状的知识间的主线索,将串联结构融合成块状结构。近似性结构的横向重构,可以帮助学生认识知识与方法之间的内在联系,以整体综合的方式把握知识的结构,培养学生思维的广度与深度。
如人教版教材的“植树问题”,一直是学生的学习难点。究其原因,就是模型记忆上的负担,以及实际情况和模型对接让学生感觉负担大。基于这样的认识,对“植树问题”单元进行了重组。(见表6)
“植树问题”单元的重组实现了两个目标:一是坚持学生立场,丰富学生思维厚度。站在学生认知角度重构植树问题,打造“一题两变式”。这样大幅度减少了学生记忆和理解上的负担,增加了学生自主探索的时间与空间。二是关注数学本质,横向架构块状结构。植树问题的本质是对应思想,只要将“一一对应”思想植入了学生内心,其他情况都是一一对应的变化而已。
2.递进性结构重组
递进性结构重组,就是将单元内容以先整体再局部的结构进行重组,在递进中感悟知识的共性和差异性。
以人教版教材的“长方体的体积”为例,原单元以长方体的体积计算为起点,依次教学正方体的体积、圆柱的体积、圆锥的体积,这样的编排没有体现柱体的特征,学生感受不到知识的整体发展过程。重构采用整体感悟的策略,补充三棱柱的教学,打通三棱柱、四棱柱、五棱柱……以至圆柱,学生能整体感知直柱体的体积计算方法都是底面积乘高。这样的重组能让学生整体感知由面到体的过程,进而从中生成表面积和体积这一类计算的共同表征。补充三棱柱、四棱柱等概念与体积计算的学习,意在建立知识面的块状联结,让学生经历从平面图形的累积形成柱体的整体思考。
每个单元内容的重组,都坚持了“学生立场”,遵循学科逻辑与学生认知逻辑,从八个维度进行了单元教学整体重构,每一个维度的重构策略与学生的认知能力紧密贴合,突出单元学习的关键与重点,帮助学生刻画了一个个单元学习主题内容清晰、连续的学习轨迹,实现了深度学习,打通了知识到核心素养的通道。
(责编 金 铃)
